LEHRSATZ DES PYTHAGORAS

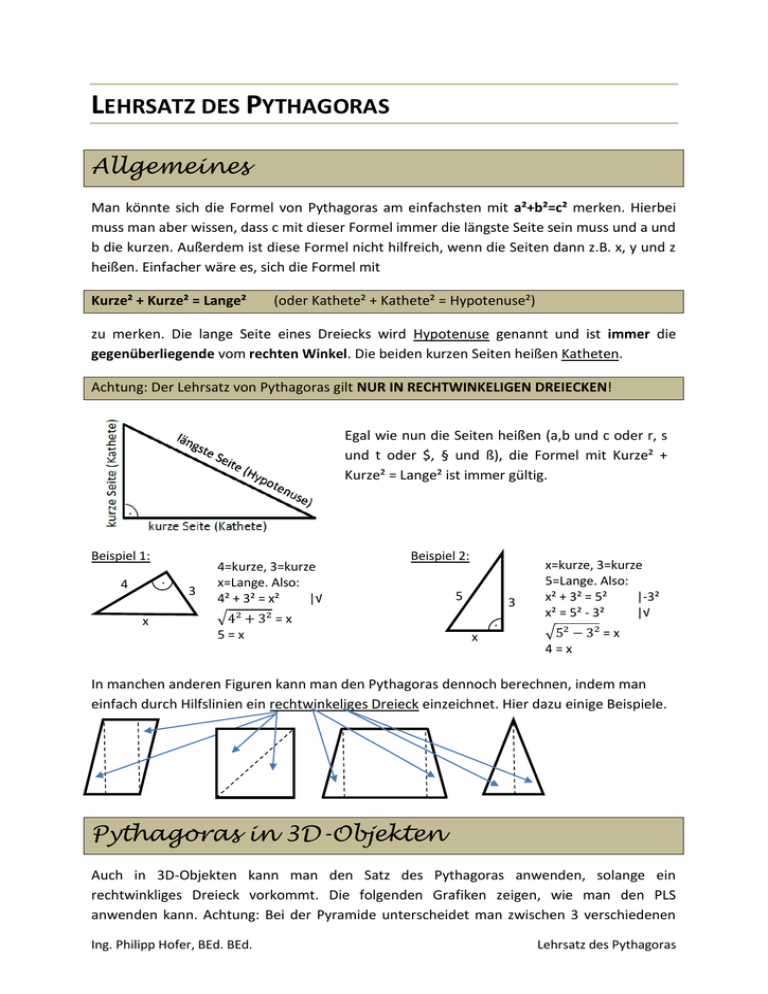
LEHRSATZ DES PYTHAGORAS
Allgemeines
Man könnte sich die Formel von Pythagoras am einfachsten mit a²+b²=c² merken. Hierbei
muss man aber wissen, dass c mit dieser Formel immer die längste Seite sein muss und a und
b die kurzen. Außerdem ist diese Formel nicht hilfreich, wenn die Seiten dann z.B. x, y und z
heißen. Einfacher wäre es, sich die Formel mit
Kurze² + Kurze² = Lange²
(oder Kathete² + Kathete² = Hypotenuse²)
zu merken. Die lange Seite eines Dreiecks wird Hypotenuse genannt und ist immer die
gegenüberliegende vom rechten Winkel. Die beiden kurzen Seiten heißen Katheten.
Achtung: Der Lehrsatz von Pythagoras gilt NUR IN RECHTWINKELIGEN DREIECKEN!
Egal wie nun die Seiten heißen (a,b und c oder r, s
und t oder $, § und ß), die Formel mit Kurze² +
Kurze² = Lange² ist immer gültig.
Beispiel 1:
.
4
x
3
4=kurze, 3=kurze
x=Lange. Also:
4² + 3² = x²
|√
√4² + 3² = x
5=x
Beispiel 2:
5
3
.
x
x=kurze, 3=kurze
5=Lange. Also:
x² + 3² = 5²
|-3²
x² = 5² - 3²
|√
√5² − 3² = x
4=x
In manchen anderen Figuren kann man den Pythagoras dennoch berechnen, indem man
einfach durch Hilfslinien ein rechtwinkeliges Dreieck einzeichnet. Hier dazu einige Beispiele.
Pythagoras in 3D-Objekten
Auch in 3D-Objekten kann man den Satz des Pythagoras anwenden, solange ein
rechtwinkliges Dreieck vorkommt. Die folgenden Grafiken zeigen, wie man den PLS
anwenden kann. Achtung: Bei der Pyramide unterscheidet man zwischen 3 verschiedenen
Ing. Philipp Hofer, BEd. BEd.
Lehrsatz des Pythagoras
Höhen, nämlich h (Gesamthöhe des Körpers), ha (Höhe des vorderen und hinteren Dreiecks)
und hb (Höhe der seitlichen Dreiecke. Die beiden Höhen ha und hb sind größer als die Höhe h.
d2
d3
a
a
a
d1
a
a
d1² = a² + a²
d2² = a² + a²
d3² = a² + a²
d² = d1² + a² = a² + a² + a²
d3
d2
d1
a
a
h
d
h
h
d1
b
a
d1
b
a
d1² = a² + b²
d
d2² = a² + h²
a
d3² = b² + h²
b
d² = d1² + h² = a² + b² + h²
s
s
h
hb
a
𝑎
hb² = (2)² + h²
b
ha
hb
b
a
𝑏
s² = hb² + (2)²
Ing. Philipp Hofer, BEd. BEd.
h
ha
b
a
𝑏
ha² = (2)² + h²
s
h
b
a
a
𝑎
s² = ha² + (2)²
𝑑
s² = ( 2 )² + h²
Lehrsatz des Pythagoras