Formeln und Wissenswertes zu Drei,- Vier- und n

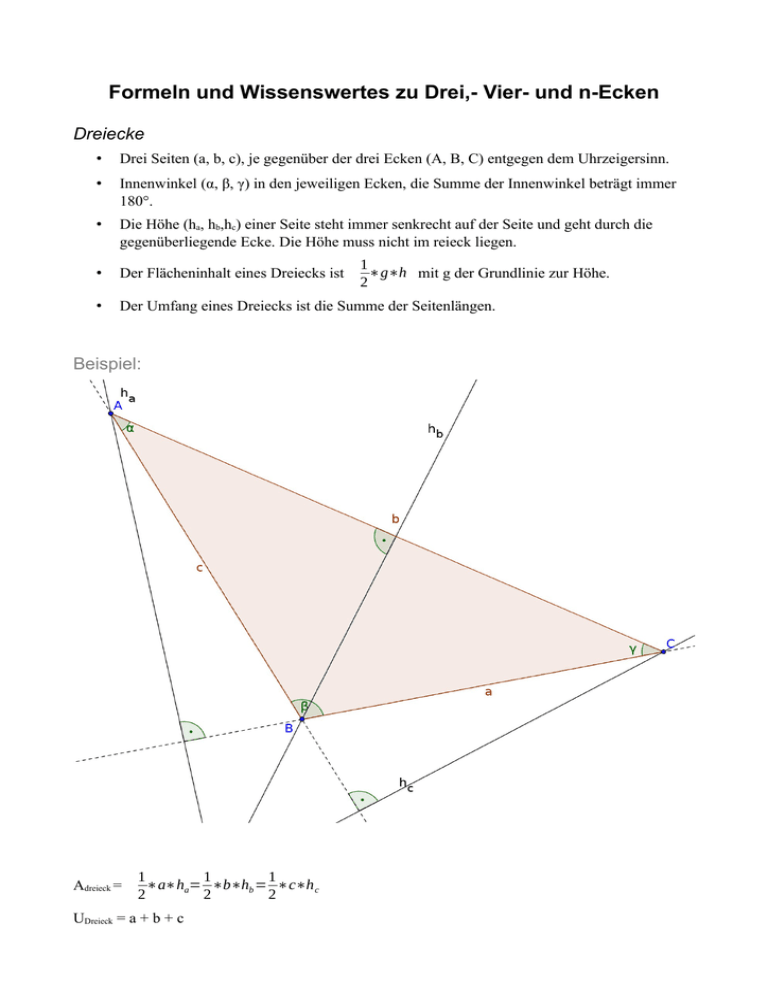
Formeln und Wissenswertes zu Drei,- Vier- und n-Ecken
Dreiecke
•
Drei Seiten (a, b, c), je gegenüber der drei Ecken (A, B, C) entgegen dem Uhrzeigersinn.
•
Innenwinkel (α, β, γ) in den jeweiligen Ecken, die Summe der Innenwinkel beträgt immer
180°.
•
Die Höhe (ha, hb,hc) einer Seite steht immer senkrecht auf der Seite und geht durch die
gegenüberliegende Ecke. Die Höhe muss nicht im reieck liegen.
•
Der Flächeninhalt eines Dreiecks ist
•
Der Umfang eines Dreiecks ist die Summe der Seitenlängen.
Beispiel:
Adreieck =
1
1
1
∗a∗ha= ∗b∗hb = ∗c∗h c
2
2
2
UDreieck = a + b + c
1
∗g∗h mit g der Grundlinie zur Höhe.
2
Unterschiedliche Vierecke
Auflistung:
•
Allgemeines Viereck: Eine Form mit 4 Ecken und 4 Seiten, die sich nicht kreuzen.
Summe der Innenwinkel ist 360° (die Summe der Innenwinkel 2er Driecke)
•
Rechteck: Alle Winkel betragen 90°, jeweils die gegenüberliegenden Seiten sind gleich lang
und parallel.
•
Quadrat: Alle Winkel betragen 90°, alle Seiten sind gleich lang, gegenüberliegende Seiten
sind parallel.
•
Raute: Gegenüberliegende Winkel sind gleich groß, alle Seiten sind gleich lang,
gegenüberliegende Seiten sind parallel.
•
Drachen (Rombus): Je zwei benachbarte Seiten sind gleich lang.
•
Parallelogramm: Gegenüberliegende Winkel sind gleich groß, gegenüberliegende Seiten
sind gleich lang und parallel.
•
Trapez: Zwei Seiten sind parallel.
Es gilt:
•
Jedes Quadrat ist: ein Rechteck, eine Raut, ein Parallelogramm, ein Drache.
•
Jede Raute ist ein Drache.
Formeln für Fläche und Umfang:
Rechteck
a·b
a und b sind Länge und Breite des Rechtecks
Quadrat
a2
a ist die Seitenlänge des Quadrates
Parallelogramm
g·h
g ist eine Seitenlänge, h der Abstand der parellelen Seite zu g
Trapez
½·h·(a + c)
a und c sind die Seitenlängen der zueiander parallelen Seiten,
h deren Abstand voneinander
Raute und
Rhombus
½·d1·d2 = a·h
= a²·sin α
d1 und d2 sind die Diagonalenlängen, α der Winkel, den die
Seiten a und d bilden, und h die Höhe auf der Seite a
Quelle: http://www.arndt-bruenner.de/mathe/geometrie/flaechen1.htm
Allegemeine Vielecke:
Jedes Vieleck lässt sich in Dreiecke / bekannte Vielecke zerlegen,
so dass man durch die Summe der Einzelflächen die
Gesamtfläche bestimmen kann.
Der Umfang ist wie immer die Summe aller Seitenlängen.
Quelle:
http://gfs.khmeyberg.de/0809/0809Klasse7dMa/0809Material7dMa/200901157dMa01.png
Regelmäßige n-Ecke (gleichseitige Vielecke)
Regelmäßige n-Ecke kann man in n gleichflächige Dreiecke
(Segmente) zerlegen (sternförmig vom Mittelpunkt aus). Hierfür
gilt für die Konstruktion:
Innenwinkel α:
α=
n−2
∗180 °
n
hier: n= 6, α = 120°
Mittelpunktswinkel (Zentriwinkel) μ:
μ=360
°
, hier μ=60°
n
Außerdem benötigt man zum Bestimmen der Fläche die
Seitenlänge a, sowie die Höhe ha ( hier ri ). Letztere muss evtl.
gemessen werden.
Quelle: http://de.wikipedia.org/wiki/Regelm%C3%A4%C3%9Figes_Polygon
Je höher die Anzahl der Ecken (n) wird, desto mehr ähnelt das n-Eck einem Kreis. Die beiden
Radien ri (Inkreis) und ra (Umkreis) werden immer ähnlicher und das Verhältnis von Umfang (n*a)
und doppeltem Innen- / Außenradius geht immer mehr gegen die Kreiszahl π.
Exkursion – Der Kreis
Ein Kreis kann als regelmäßiges n-Eck mit unendlich vielen Ecken angesehen werden. Das hat zur
Folge, dass die einzelnen Segmente unendlich klein werden und α gegen 180° geht. Da man dies
schlecht verstehen und unmöglich zeichnen kann ( ;-) ) gilt für Kreise:
Der Umfang eines Kreises:
UKreis = 2 * π * r = π * d
(mit Durchmesser d = doppelter Radius; π ≈ 3,14156 [TR])
Die Fläche eines Kreises:
AKreis = π * r² = π *
d
4
Der Kreis ist etwas kleiner (π/4) als das ihn umschließende Quadrat mit Seitenlänge d.