2016_02_03, Rationale Zahlen auf der Zahlengeraden

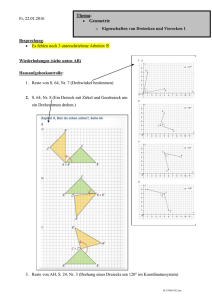
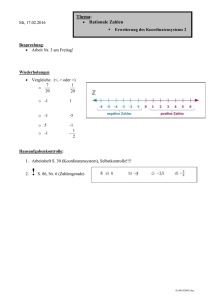
Mi, 03.02.2016
Thema:
 Rationale Zahlen (positive und negative Zahlen)
o Einführung
o Rationale Zahlen auf der Zahlengerade
Besprechung:
 Es fehlen immer noch 2 unterschriebene Arbeiten : Pejman, Marveth,

Arbeit Nr. 3:
Fr, 19.02.2016
Arbeit Nr. 4:
Fr, 03.06.2016
Wiederholungen
 Was versteht man unter einer „mathematischen Aussage“?
o Für ein n-Eck gilt für die Summe der Innenwinkel die Berechnungsformel: (n-2)*180°
o Jedes Quadrat ist ein Parallelogramm.
o Jede Raute ist ein Parallelogramm.
o 1 ist eine Primzahl.
o Jedes Parallelogramm ist eine Raute.
 Wie widerlegt man eine allgemeine Aussage in der Mathematik?
 Wie beweist man eine allgemeine Aussage in der Mathematik?
Hausaufgabenkontrolle:
1. Wiederholendes Lesen der Seiten 69, 70
2. S. 71, Nr. 1 (besondere Vierecke), Nr. 4 (besondere Dreiecke)
3. S. 72, Nr. 12 (mathematische Aussagen prüfen, besondere Vierecke) (Selbstkontrolle)
a. Jede Raute ist ein Drachen.
b. Jeder symmetrischer Drachen ist ein Parallelogramm.
c. Jedes Trapez ist ein Rechteck.
d. Rechteck ist ein Trapez.
D:\481356800.doc
Thema: Rationale Zahlen - Einführungsspiele
1. Bisher kennst du die Menge der positiven Zahlen (natürliche Zahlen, Brüche, Dezimalzahlen).
Nun kommen die Negativen zahlen hinzu. Man nennt die Gesamtheit aller positiver und
negativer Zahlen Menge der rationalen Zahlen (Bezeichnung: Q ).
2. Woher kennst du negative Zahlen aus dem Alltag?
3. Spiel: Guthaben und Schulden (siehe Buch S. 82)
4. [Spiel: Hin und her (siehe Buch S. 83)]
5. Gemeinsames Lesen S. 84
Hausaufgaben:
1. Sicher ins Kapitel III, S. 205, Nr. 1, 2, 3, 4, Nr. 5 freiwillig, Lösungen zur Selbstkontrolle auf
S. 237
2. S. 84 lesen.
D:\481356800.doc
Spielprotokolle von: _______________________
Datum:
Blau sind Gutscheine. Rot sind Schuldscheine.
1. 20 x blau und 20 x rot bedeutet Kontostand: 0
2. 11 x blau und 20 x rot bedeutet Kontostand:
3. 20 x blau und 11 x rot bedeutet Kontostand:
4. 25 x blau und 40 x rot bedeutet Kontostand:
Probespiel:
Alter Kontostand
Kontobewegung
Neuer Kontostand
1. Runde
0 (20 x blau, 20 x rot)
-
5
-5
2. Runde
-5
+
-1
-6
3. Runde
-6
4. Runde
5. Runde
Hauptspiel:
Alter Kontostand
1. Runde
Kontobewegung
Neuer Kontostand
0 (20 x blau, 20 x rot)
2. Runde
3. Runde
4. Runde
5. Runde
6. Runde
7. Runde
8. Runde
9. Runde
10. Runde
11. Runde
12. Runde
13. Runde
14. Runde
15. Runde
16. Runde
17. Runde
18. Runde
19. Runde
20. Runde
D:\481356800.doc
Wiederholungen:
1. Gesetze rund um Nebenwinkel, Gegenwinkel, Stufenwinkel.
o Die Summe der Innenwinkel im Dreieck beträgt
______________
o Die Summe der Innenwinkel im Viereck beträgt
______________
o Die Summe der Innenwinkel im Fünfeck beträgt ______________
o Die Summe der Innenwinkel im n-Eck beträgt
______________
2. Bestimme die roten Winkel α, β, γ. Begründe!
3. Zeichne die Symmetrieachse(n) in die Buchstaben ein.
D:\481356800.doc
4. Wie finde ich im Koordinatensystem den Punkt A mit den Koordinaten (1/3)?
5. Erkläre, wie man einen Punkt mit Hilfe von Geodreieck (und Zirkel) an einer Achse spiegeln
kann.
6.
7.
8.
9.
Zeichne jeweils ein Beispiel für Scheitel-, Neben- und Stufenwinkel.
Die Summe der Innenwinkel im n-Eck beträgt
______________
Die Summe der Innenwinkel im 42-Eck beträgt
______________
Beschrifte die Dreiecke und benenne die wichtigsten Eigenschaften einer Achsenspiegelung.
10. Achsenspiegelung: A(4/1), B(6/6), C(1/3), D(4/3)
o Zeichne das Viereck ABCD ein.
o Spiegle es an der Achse PQ mit P(0/0) und Q(6/6).
11. Bei einer Achsenspiegelung hat A(5/6) den Bildpunkt A´(1/4).
D:\481356800.doc
o Bestimme die Spiegelachse.
12. Drehungen
o Trage das Drehzentrum Z(3/1) sowie den Punkt A(7/2) in das
Koordinatensystem ein.
o Drehe den Punkt A um 75° um das Drehzentrum Z.
13.
D:\481356800.doc