2016_02_17, Rationalen Zahlen, Erweiterung des

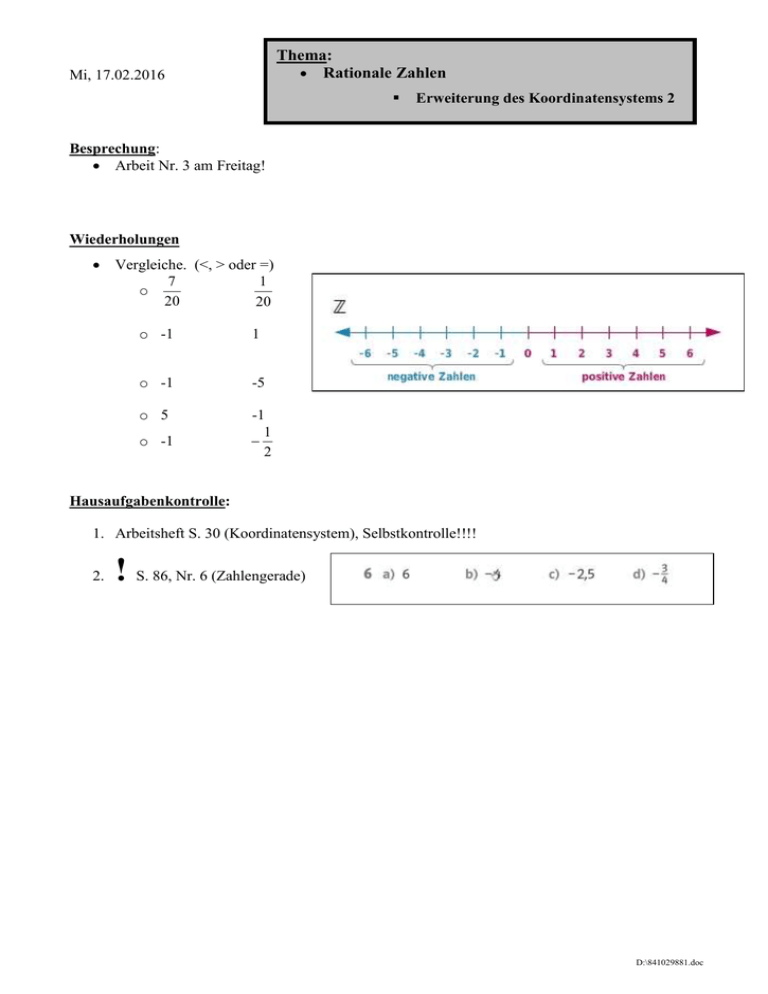
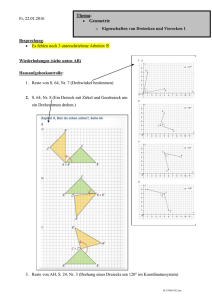
Thema:
 Rationale Zahlen
Mi, 17.02.2016

Erweiterung des Koordinatensystems 2
Besprechung:
 Arbeit Nr. 3 am Freitag!
Wiederholungen
 Vergleiche. (<, > oder =)
1
7
o
20
20
o -1
1
o -1
-5
o 5
-1
1

2
o -1
Hausaufgabenkontrolle:
1. Arbeitsheft S. 30 (Koordinatensystem), Selbstkontrolle!!!!
2.
! S. 86, Nr. 6 (Zahlengerade)
D:\841029881.doc
Themen:
Fragen zur Arbeit
Rationale Zahlen auf der Zahlengeraden 3
Welche Zahl liegt auf der Zahlengeraden in der Mitte von
a. 2 und 6
Abstand =
, also liegt ___________________________ in der Mitte
b. -5 und -1
Abstand =
, also liegt ___________________________ in der Mitte
c. -6 und 6
Abstand =
, also liegt ___________________________ in der Mitte
d. -4 und 2
Abstand =
, also liegt ___________________________ in der Mitte
e. -2 und 5
Abstand =
, also liegt ___________________________ in der Mitte
f. 2 und 5
Abstand =
, also liegt ___________________________ in der Mitte
g. -6 und 4
Abstand =
, also liegt ___________________________ in der Mitte
h. -3 und 5
Abstand =
, also liegt ___________________________ in der Mitte
i. -1 und 4
Abstand =
, also liegt ___________________________ in der Mitte
Übungen:
Übungen zu Erweiterung des Koordinatensystems
1. AB Rationale Zahlen: Figuren im Koordinatensystem (Niveau 1)
2. AB Rationale Zahlen: Figuren im Koordinatensystem (Niveau 2)
D:\841029881.doc
Anordnen
1. Einführungstext, S. 88 Mitte (Betrag, Gegenzahl, kleiner, größer)
2. Übungen
a. Arbeitsheft S. 31, Nr. 1 (Zahl und Gegenzahl auf der Zahlengeraden)
b. Arbeitsheft S. 31, Nr. 2, 3, 4, 5 (Zahl und Gegenzahl, Betrag)
c. S. 89, Nr. 3 und 5 mündlich am Smartboard
Hausaufgaben:
1. Lesen. Einführungstext, S. 88 (Betrag, Gegenzahl, kleiner, größer)
2. Arbeitsheft S. 31, Nr. 5 (Temperaturen aus einem Diagramm ablesen)
3. Arbeitsheft S. 32, Selbstkontrolle!!!!!!! (Rationale Zahlen vergleichen)
4. S. 86, Nr. 8, Selbstkontrolle, (Zahlengerade)
Bereite dich weiter gewissenhaft auf die Arbeit Nr. 3 am Freitag vor.
D:\841029881.doc
Wiederholungen:
1. Gesetze rund um Nebenwinkel, Gegenwinkel, Stufenwinkel.
o Die Summe der Innenwinkel im Dreieck beträgt
______________
o Die Summe der Innenwinkel im Viereck beträgt
______________
o Die Summe der Innenwinkel im Fünfeck beträgt ______________
o Die Summe der Innenwinkel im n-Eck beträgt
______________
2. Bestimme die roten Winkel α, β, γ. Begründe!
3. Zeichne die Symmetrieachse(n) in die Buchstaben ein.
D:\841029881.doc
4. Wie finde ich im Koordinatensystem den Punkt A mit den Koordinaten (1/3)?
5. Erkläre, wie man einen Punkt mit Hilfe von Geodreieck (und Zirkel) an einer Achse spiegeln
kann.
6.
7.
8.
9.
Zeichne jeweils ein Beispiel für Scheitel-, Neben- und Stufenwinkel.
Die Summe der Innenwinkel im n-Eck beträgt
______________
Die Summe der Innenwinkel im 42-Eck beträgt
______________
Beschrifte die Dreiecke und benenne die wichtigsten Eigenschaften einer Achsenspiegelung.
10. Achsenspiegelung: A(4/1), B(6/6), C(1/3), D(4/3)
o Zeichne das Viereck ABCD ein.
o Spiegle es an der Achse PQ mit P(0/0) und Q(6/6).
11. Bei einer Achsenspiegelung hat A(5/6) den Bildpunkt A´(1/4).
D:\841029881.doc
o Bestimme die Spiegelachse.
12. Drehungen
o Trage das Drehzentrum Z(3/1) sowie den Punkt A(7/2) in das
Koordinatensystem ein.
o Drehe den Punkt A um 75° um das Drehzentrum Z.
13. Was versteht man unter einer „mathematischen Aussage“?
o Für ein n-Eck gilt für die Summe der Innenwinkel die Berechnungsformel: (n2)*180°
o Jedes Quadrat ist ein Parallelogramm.
o Jede Raute ist ein Parallelogramm.
o 1 ist eine Primzahl.
o Jedes Parallelogramm ist eine Raute.
14. Wie widerlegt man eine allgemeine Aussage in der Mathematik?
15. Wie beweist man eine allgemeine Aussage in der Mathematik?
16. Addition und Subtraktion von rationalen Zahlen
a. 320 – (+200) =
b. -90 – (-50) =
c. -50 + (+60) =
d. 55 – (+85) =
17. Schreibe den Bruch als Dezimalbruch + als Prozentangabe
7
o  =
25
D:\841029881.doc
3

5
18. Schreibe als vollständig gekürzten Bruch
o 
o -9,3 =
o -0,125 =
19. Welche Zahl liegt auf der Zahlengeraden in der Mitte von
a. 2 und 6
Abstand =
, also liegt __________________________ in der
Abstand =
, also liegt __________________________ in der
Abstand =
, also liegt __________________________ in der
Abstand =
, also liegt __________________________ in der
Abstand =
, also liegt __________________________ in der
Mitte
b. -5 und -1
Mitte
c. -6 und 6
Mitte
d. -4 und 2
Mitte
e. -2 und 5
Mitte
20.
D:\841029881.doc