Einführung der rationalen Zahlen
Werbung
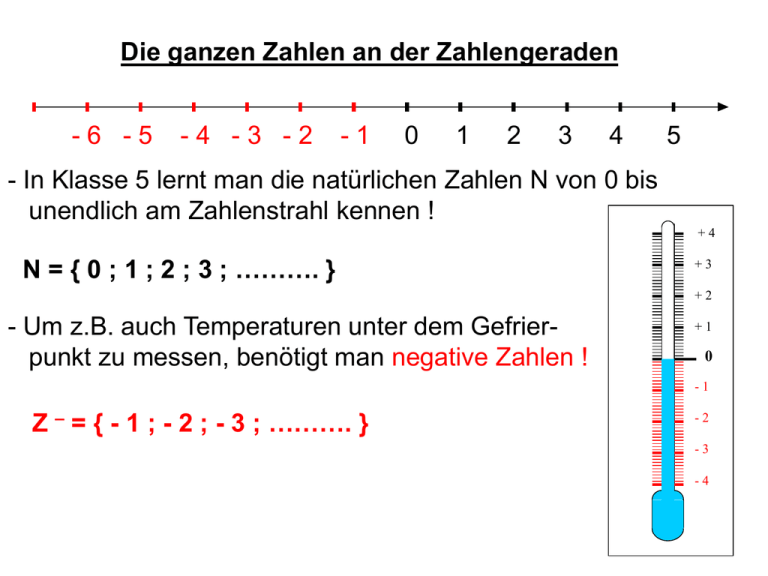
Die ganzen Zahlen an der Zahlengeraden
-6 -5
-4 -3 -2
-1
0
1
2
3
4
5
- In Klasse 5 lernt man die natürlichen Zahlen N von 0 bis
unendlich am Zahlenstrahl kennen !
+4
N = { 0 ; 1 ; 2 ; 3 ; ………. }
+3
+2
- Um z.B. auch Temperaturen unter dem Gefrierpunkt zu messen, benötigt man negative Zahlen !
+1
0
-1
Z – = { - 1 ; - 2 ; - 3 ; ………. }
-2
-3
-4
Merke:
Positive und negative Zahlen nennt man die
Menge Z der ganzen Zahlen !
Z = {….. …. ; - 3 ; - 2 ; - 1 ; 0 ; + 1 ; + 2 ; + 3 ; ……. }
Negative ganze Zahlen Z -
Positive ganze Zahlen Z +
Ganze Zahlen Z
Die rationalen Zahlen an der Zahlengeraden
-4
+4
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
Erweitert man die ganzen Zahlen mit positiven und negativen
Bruchzahlen, so erhält man die Menge Q der rationalen Zahlen.
Merke:
- Jede Zahl hat eine Gegenzahl !
- Zahl und Gegenzahl haben den selben Abstand
von der Null.
- Man nennt den Abstand einer Zahl von der Null
auch den Betrag der Zahl und man schreibt
|-4|=|+4|