ℕ ℤ ℚ ℝ - MindMeister

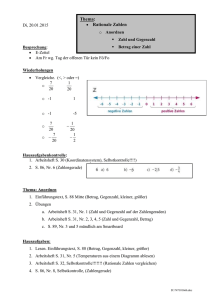
Zahlenmengen
Zahlenmengen
ℝ
ℚ
ℤ
ℕ
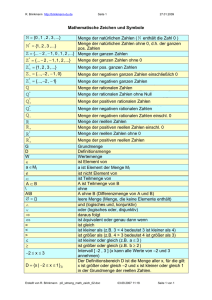
ℕ: Natürliche Zahlen
ℕ = {0, 1, 2, 3, 4, 5, … }
ℤ: Ganze Zahlen
ℤ = { … -3, -2, -1, 0, 1, 2, 3, … }
Die Menge der Natürlichen Zahlen ist echte Teilmenge der ganzen Zahlen: ℕ ᴄ ℤ.
ℚ: Rationale Zahlen
𝑎
ℚ = { 𝑏 | a ∈ ℤ und b ∈ ℤ \ {0} }
Die rationalen Zahlen lassen sich als abbrechende oder periodischen Dezimalzahlen
beschreiben. Die Menge der natürlichen Zahlen und die Menge der ganzen Zahlen
sind Teilmenge der rationalen Zahlen: ℕ ⊆ ℤ ⊆ ℚ
ℝ: Reelle Zahlen
Die Menge der reellen Zahlen enthält die rationalen Zahlen und die irrationalen
Zahlen, wie z.B. √3; π; e.
Die irrationalen Zahlen lassen sich nicht als abbrechende oder periodische
Dezimalzahlen schreiben,
Die Menge der rationalen Zahlen ist Teilmenge der reellen Zahlen: ℕ ⊆ ℤ ⊆ ℚ ⊆ ℝ
Primzahlen
Eine natürliche Zahl, welche nur durch sich selbst und durch 1 teilbar ist, heißt
Primzahl. Jede natürliche Zahl > 1 kann man eindeutig als Produkt von Primzahlen
darstellen. (Primfaktorzerlegung)
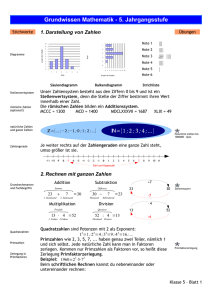
Primzahlen: 2, 3, 5, 7, 11, 13, 17, 19, …
Primfaktorzerlegung: 210 = 2 × 3 × 5 × 7
Zahlengerade
Wenn a < b, dann liegt der Punkt, der der Zahl a entspricht, auf der Zahlengeraden
links von dem Punkt, der der Zahl b entspricht.
Gegenzahl
Zu einer Zahl a heißt die Gegenzahl –a Gegenzahl von a. Die Punkte die der Zahl
und Gegenzahl entsprechen, haben auf der Zahlengeraden den selben Abstand von
der Null. Die Summe von Zahl und Gegenzahl ist 0: a + (-a) = 0.
Betrag einer Zahl
-a
0
Für den Betrag |a| einer reellen Zahl a gilt:
|a| =
a, falls a > 0
0, falls a = 0
-a, falls a < 0
a
Die Punkte, die Zahlen mit
demselben Betrag
entsprechen, sind auf der
Zahlengeraden gleich weit von
der Null entfernt