2015_01_27, Rationalen Zahlen, Addieren und Subtrahieren einer

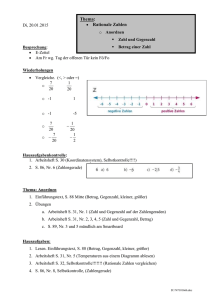
Thema:
 Rationale Zahlen
Di 27.01.2015
o Addieren und Subtrahieren einer positiven Zahl
(Gutscheine aufnehmen und abgeben)
Besprechung:
 Restliche Arbeiten (14!!!)
 E-Zettel
Wiederholungen
 2+5=
Hinweis auf Rechenzeichen und Vorzeichen.
 Das Plus-Vorzeichen bedeutet Guthaben.
 Das Minus-Vorzeichen bedeutet Schulden.
 Das Plus-Rechenzeichen bedeutet aufnehmen.
 Das Minus-Rechenzeichen bedeutet abgeben.
 -2 + 5 =
 2–5=
 -2 – 5 =
 Setze für □ eines der Zeichen < oder > oder = und für ∆ eine passende Ziffer.
a) -0,4 > -0,∆
b) -33,7 < ∆,6
c) 

2
1
□ 
6
5
Gib eine Zahl an, die zwischen den angegebenen Zahlen liegt.
a) 9,3 und 9,4
b) 
5
1
und 
6
2
c) -0,4 und -0,45
Hausaufgabenkontrolle:
1. S. 89, Nr. 5, 6, 7
2. S. 90, Nr. 14 (Whg. Winkelgesetze, Selbstkontrolle)
3. S. 90, Nr. 8, 9 (Anordnen) (Kannst das schon? Selbstkontrolle)
4. S. 86, Nr. 8, Selbstkontrolle, (Zahlengerade)
D:\481356958.doc
Thema: Addieren und Subtrahieren einer positiven Zahl
1. Beantworte (mündlich) die Fragen zu dem Spiel „Guthaben und Schulden“ auf S. 82.
a. Wie stellt man am Ende fest, wer gewonnen hat?
b. Kann das Spiel unentschieden ausgehen?
c. Wie geht man vor, wenn jemand nicht mehr genug Schuldscheine oder Gutscheine hat?
1.
-2 – 5 =
2.
-2 – (-5) =
d. Wie kann man das Spiel auch ohne Gutscheine spielen?
2. Tafel: Positive ganze Zahlen und positive Dezimalzahlen addieren und subtrahieren
a. -4 + 6 =
b. 15 – 21 =
c. -2,3 – 0,6 =
d. 3,4 – 5,5 =
3. Veranschaulichung am Zahlenstrahl
Gemeinsames lesen der S. 91
4. Übung, Arbeitsheft, S. 33, Nr. 1, 2, 3
5. Tafel: Positive Brüche addieren und subtrahieren
2
5
7
5
a.   
b. 
2 7
 
5 5
c. 
2 7
 
5 10
6. Übung, Arbeitsheft, S. 33, Nr. 4, 5, 6
Hausaufgaben:
1. Reste von Übung, Arbeitsheft, S. 33,
2. S. 92, Nr. 1, 2, 3, 4, 5, 6, (7)
D:\481356958.doc
Wiederholungen
1. Was versteht man unter einer „mathematischen Aussage“?
a. Für ein n-Eck gilt für die Summe der Innenwinkel die Berechnungsformel: (n-2)*180°
b. Jedes Quadrat ist ein Parallelogramm.
c. Jede Raute ist ein Parallelogramm.
d. 1 ist eine Primzahl.
e. Jedes Parallelogramm ist eine Raute.
2. Wie widerlegt man eine allgemeine Aussage in der Mathematik?
3. Wie beweist man eine allgemeine Aussage in der Mathematik?
4.
Zahl
Gegenzahl
Betrag
3
5,33
-7,5
1,2
5.
Markiere auf dem Zahlenstrahl
a. | | < 3
b. | | < 6
c. | | > 5
2
6. Welche der Zahlen -6,8; 65; -0,05;  9 ; -80; 0 hat den größten (kleinsten) Betrag?
3
7.
D:\481356958.doc