6 Dividieren von Dezimalzahlen
Werbung
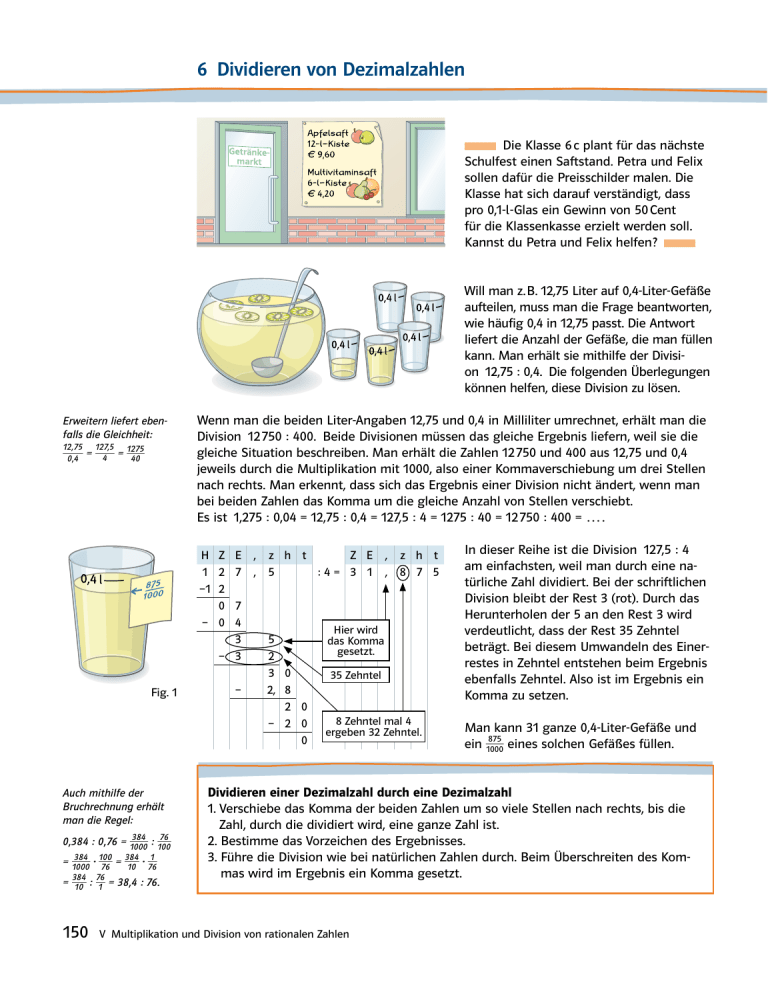
6 Dividieren von Dezimalzahlen Die Klasse 6 c plant für das nächste Schulfest einen Saftstand. Petra und Felix sollen dafür die Preisschilder malen. Die Klasse hat sich darauf verständigt, dass pro 0,1-ø-Glas ein Gewinn von 50 Cent für die Klassenkasse erzielt werden soll. Kannst du Petra und Felix helfen? Will man z. B. 12,75 Liter auf 0,4-Liter-Gefäße aufteilen, muss man die Frage beantworten, wie häufig 0,4 in 12,75 passt. Die Antwort liefert die Anzahl der Gefäße, die man füllen kann. Man erhält sie mithilfe der Division 12,75 : 0,4. Die folgenden Überlegungen können helfen, diese Division zu lösen. Erweitern liefert ebenfalls die Gleichheit: 12,75 0,4 127,5 4 1275 40 _ = _ = _ Wenn man die beiden Liter-Angaben 12,75 und 0,4 in Milliliter umrechnet, erhält man die Division 12 750 : 400. Beide Divisionen müssen das gleiche Ergebnis liefern, weil sie die gleiche Situation beschreiben. Man erhält die Zahlen 12 750 und 400 aus 12,75 und 0,4 jeweils durch die Multiplikation mit 1000, also einer Kommaverschiebung um drei Stellen nach rechts. Man erkennt, dass sich das Ergebnis einer Division nicht ändert, wenn man bei beiden Zahlen das Komma um die gleiche Anzahl von Stellen verschiebt. Es ist 1,275 : 0,04 = 12,75 : 0,4 = 127,5 : 4 = 1275 : 40 = 12 750 : 400 = … . H Z E 1 2 7 –1 2 0 7 – 0 4 3 – 3 Fig. 1 Auch mithilfe der ­Bruchrechnung erhält man die Regel: 384 76 _ 0,384 : 0,76 = _ 1000 : 100 384 100 384 1 _ · _ =_ 1000 · _ 76 = 10 76 384 76 = _ : _ 1 = 38,4 : 76. 10 150 – , , z h t Z E 5 :4= 3 1 5 2 3 0 2, 8 2 0 – 2 0 0 , , z h t 8 7 5 Hier wird das Komma gesetzt. 35 Zehntel 8 Zehntel mal 4 ­ergeben 32 Zehntel. In dieser Reihe ist die Division 127,5 : 4 am einfachsten, weil man durch eine natürliche Zahl dividiert. Bei der schriftlichen Division bleibt der Rest 3 (rot). Durch das Herunterholen der 5 an den Rest 3 wird verdeutlicht, dass der Rest 35 Zehntel beträgt. Bei diesem Umwandeln des Einerrestes in Zehntel entstehen beim Ergebnis ebenfalls Zehntel. Also ist im Ergebnis ein Komma zu setzen. Man kann 31 ganze 0,4-Liter-Gefäße und 875 ein _ 1000 eines solchen Gefäßes füllen. Dividieren einer Dezimalzahl durch eine Dezimalzahl 1. Verschiebe das Komma der beiden Zahlen um so viele Stellen nach rechts, bis die Zahl, durch die dividiert wird, eine ganze Zahl ist. 2. Bestimme das Vorzeichen des Ergebnisses. 3. Führe die Division wie bei natürlichen Zahlen durch. Beim Überschreiten des Kommas wird im Ergebnis ein Komma gesetzt. V Multiplikation und Division von rationalen Zahlen Hat die Zahl, durch die geteilt wird, mehr Nachkommastellen als die zu teilende Zahl, so muss man Nullen anhängen: 4,62 : 0,028 = 4620 : 28. Bei der Division von Dezimalzahlen kann eine Überschlagsrechnung nützlich sein. Dabei bieten sich die folgenden zwei Schritte an: 1. Verschiebe das Komma so, dass die Zahl, durch die geteilt wird, nur eine Stelle vor dem Komma hat. 2. Runde die Zahl, durch die geteilt wird, auf die Einerstelle. Runde nun die zu teilende Zahl so, dass du die Division im Kopf ausführen kannst. Beispiel 1 Kommaverschiebung vor der Division Berechne. a) 5,865 : (– 1,7) b) 15 : 1,25 Lösung: a) 5,865 : (– 1,7) = 58,65 : (– 17) = – 3,45 b) 15,00 : 1,25 = Å500 : 125 = 12 – 5Å – 125 å6 250 – 68 – 250 85 0 – 85 Bei der Kommaverschiebung um zwei Stel 0 len muss man zwei Nullen ­anhängen. Beispiel 2 Überschlag durch Kommaverschiebung und Runden Überschlage zuerst und überprüfe dann mit dem Taschenrechner: 1,9404 : 0,462. Lösung: Überschlag: Rechnung: 1,9404 : 0,462 = 19,404 : 4,62 ≈ 20 : 5 = 4 1,9404 : 0,462 = 4,2 Zuerst wird die Zahl, durch die geteilt wird, auf eine Stelle vor dem Komma gerundet: 5. Anschließend wird so gerundet, dass man eine durch 5 teilbare Zahl erhält: 20. Aufgaben 1 Das Ergebnis von 245 : 7 ist 35. Damit kannst du die folgenden Divisionen leicht berechnen. a) 24,5 : 7; 2,45 : 7; 0,245 : 7; 0,0245 : 7 b) 245 : 70; 24,5 : 70; 2,45 : 70; 0,245 : 70 2 Hier wurde einige Male falsch gerechnet. Verbessere die Fehler. Welche erkennt man durch Überschlagen? 3 Berechne im Kopf. Manchmal reicht ein Überschlag. a) 0,9 : 3 b)0,08 : (– 4) c) 9,0 : 3 d)(– 12,6) : 6 e) 3,6 : 9 0,12 : (– 6) 0,025 : 5 0,77 : 7 25,5 : 5 – 0,36 : 9 8,24 : 4 6,18 : (– 3) 18,27 : 9 0,039 : 13 0,084 : 12 4 t Überschlage zuerst und überprüfe dann mit dem Taschenrechner. a) 0,054 : 0,45 b)71,574 : 1,58 c) 13,224 : 23,2 d)1816,56 : 84,1 e) 27,318 : 0,087 V Multiplikation und Division von rationalen Zahlen 151 5 zu Aufgaben 5: – 3 O 200 L 15 E 4 N 50 P – 200 O 3500 S 60 P – 40 N – 50 E 1,96 L – 86,3 C 56,5 A 5,3 I 2,7 G 45,2 N 0,56 D 6 Überschlage und berechne dann schriftlich. a) 40,3 : 8 b) 127,5 : 4 c) 4,32 : (– 16) d) 1016,6 : 13 6,05 : (– 5) 322,8 : 5 54,3 : 12 – 623,9 : 17 34,2 : 9 – 337,8 : 6 100,5 : 15 11,04 : 90 e) 3,24 : 1,2 f) – 13,84 : 0,4 g) 9,216 : 3,6 h) 1,695 : 0,03 3,08 : 1,1 25,89 : (– 0,3) 29,148 : 8,4 13,6956 : 0,303 6,89 : 1,3 – 31,71 : (– 0,7) – 19,012 : (– 9,7) – 16,968 : (– 30,3) zu Aufgaben 6 e) bis h): 2,56 E Berechne im Kopf. Mit den Lösungen erhältst du am Rand das Lösungswort. a) 10 : 0,2 b)20 : 0,1 c) 36 : 0,6 d)0,8 : 0,2 e) 0,75 : 0,05 15 : (– 0,3) – 40 : 0,2 – 0,9 : 0,3 1,6 : (– 0,04) – 35 : (– 0,01) 45,3 H 3,47 N 2,8 R – 34,6 E Zur Erinnerung: _ 51 = 1 : 5 = Å,0 : 5 = 0,2 0 Å0 – Å0 0 7 Überschlage. Berechne wenn möglich im Kopf; ansonsten schriftlich. a) 5,75 : 0,5 b) 46,5 : 6,1 c) 3,6 : 0,6 d) 136,2 : 68,1 33,2 : 0,25 46,5 : 3,1 5,6 : 0,8 255,9 : 85,3 12,1 : 0,125 46,5 : 1,1 25,6 : 1,6 79,8 : 13,3 8 Rechne geschickt, indem du nur eine Rechnung schriftlich durchführst. a) 1,792 : 0,7 b) 15,12 : 3,6 c) 30,858 : 111 d) 540,1 : 49,1 1,792 : 0,07 151,2 : 36 30,858 : 11,1 54,01 : 49,1 179,2 : 0,7 1,512 : 3,6 308,58 : 0,111 5,401 : 0,491 17,92 : 0,07 1,512 : 0,36 3,0858 : 0,0111 0,5401 : 4,91 9 Schreibe mit Komma. 3 7 a) _51 b) _8 c) – _ 40 51 d) _ 12 e) _23 f) – _61 g) _91 h) _49 10 Ein Tunnel von 1,175 km Länge soll alle 30,5 m eine Lampe erhalten. Wie viele Lampen werden benötigt? Deute dein Ergebnis. 11 Ein Obstbauer hat 100 Liter Apfelsaft 8 mm gepresst und will ihn in 0,7-Liter-Flaschen abfüllen. Wie viele Flaschen kann er damit abfüllen? Wie viele Liter Apfelsaft bleiben übrig? 12 Kunststofffolien für die Küche sind etwa 0,05 mm dick. Bestimme die Anzahl der ­Lagen auf einer Rolle, die 8 mm dick gewickelt ist. Probiere es experimentell aus. 13 Zwei Dezimalzahlen werden dividiert. Wie ändert sich das Ergebnis, wenn man Bei Aufgabe 13 kann es hilfreich sein, „eine Tabelle anzulegen“. 152 a) bei einer Dezimalzahl das Komma um eine Stelle nach rechts verschiebt, b) bei der zu teilenden Dezimalzahl das Komma um eine Stelle nach rechts verschiebt und bei der anderen um eine Stelle nach links, c) bei beiden Dezimalzahlen das Komma um eine Stelle nach links verschiebt? V Multiplikation und Division von rationalen Zahlen Bist du sicher? 1 Berechne im Kopf. a) 5 : 0,2 b)– 4,5 : 0,5 c) 9,9 : 3,3 d)– 0,14 : (– 0,07) e) 9 : 0,003 2 Überschlage zuerst und berechne dann schriftlich. a) 156,96 : 0,24 b) – 27,318 : 0,087 c) 0,743 : (– 0,7) d) 3,95 : 0,32 3 An einer Baustelle werden 15,5 m3 Kies benötigt. Wie oft muss ein LKW, der 2,1 m3 Kies laden kann, fahren? 4 1 8 Schreibe als Dezimalzahl. 7 b)– _ 20 a) _ 7 c) _ 16 5 d) _43 e) – _6 14 Setze bei den Ergebnissen das Komma an die richtige Stelle. Manchmal musst du Nullen ergänzen. Schreibe auch deine Überschlagsrechnung auf. a) 26,292 : 4,2 = 626 b) 4,3296 : 0,82 = 35 c) 0,84 : 0,24 = 35 d) 518,49 : 4,2 = 12345 15 Der Rasen des Fußballfeldes im Weserstadion in Bremen ist 105 m lang und 68 m breit. Die Schnittbreite des Rasenmähers des Platzwarts ist 1,30 m. Wie oft muss der Platzwart beim Rasenmähen mindestens hin und her fahren? Welche Strecke legt er dabei zurück? 16 a) Herr Lind tankt 35,1 ø Benzin für 49,14 €. Wie viel Euro kostet 1 Liter? b) Seitdem Herr Lind das letzte Mal getankt hat, ist er 450 km gefahren und hat 35,1 ø Benzin verbraucht. Wie viel Liter Benzin hat er im Durchschnitt für 100 km gebraucht? 17 a) Wie oft passen die Körperlängen der Waldmaus und des Löwen in ihre Sprungweite? b) Finde heraus, wie das beim Grashüpfer, beim Riesenkänguru und beim Tiger ist. c) Wie weit könnte ein 1,55 m großes Kind jeweils springen, wenn es die Sprungkraft von Löwe, Maus usw. hätte? 18 Frau Cremer fährt mit einer Tankfüllung von 40 Litern einmal 700 km, das andere Mal 650 km. Vergleiche mit den Angaben im Prospekt. Internetrecherche kann helfen! Die Waldmaus Der Löwe kommt bis auf die nördlichsten Gebiete in ganz Europa und Asien vor. ist das imposanteste Raubtier Afrikas und Die Waldmaus kann im Rudel fast kommt auf die jedes Wild bis erbeuten. Körperlänge: Sprungweite: 9 cm 0,7 m nördlichsten Gebiete Körperlänge: 1,8 m in ganz Europa Sprungweite: 4,5und m Asien vor. 19 a) Wer ist im Mittel schneller: ein Eissprinter, der 500 m in 34,42 s läuft, oder ein RadKörperlänge: 9 cm fahrer, der in einer Stunde 45 km fährt? Sprungweite: 0,7 m b) Vergleiche einen Sprinter, der 100 m in 9,85 s läuft, und eine Eisschnelläuferin, die für 3000 m 3 min 57,7 s braucht. Die Waldmaus Der Löw kommt bis auf die nördlichsten Gebiete in ganz Europa und Asien vor. ist das im Raubtier kann im jedes Wil Körperlänge: Sprungweite: Körperlän Sprungw 9 cm 0,7 m Der Löwe ist das imposanteste Raubtier Afrikas und kann im Rudel fast jedes Wild erbeuten. Körperlänge: Sprungweite: 1,8 m 4,5 m 20 Ein Obsthändler bekommt eine Sendung mit 250 kg Äpfeln. Sie kostet 164,70 €. Beim Umpacken der Äpfel in 12,5-kg-Steigen stellt er fest, dass etwa 25 kg Äpfel angefault sind. Wie teuer muss der Händler eine Steige mindestens verkaufen, damit er pro Steige mindestens 4 € Gewinn macht? V Multiplikation und Division von rationalen Zahlen 153 Torraum Strafraum 16,50 m 7,5 cm Maße TippKick-Feld 124 cm Maße Fußballfeld 90 – 120 m Kick-Spielfigur in die Körpergröße eines 1,80 m großen Spielers? b) Das Tipp-Kick-Tor ist innen 9 cm breit und 6,5 cm hoch. Wie oft passen die Höhe und die Breite des Tors in ein richtiges Fußballtor, das 7,32 m breit und 2,44 m hoch ist? Vergleiche mit dem Verhältnis von Tipp-Kick-Spielfigur zu einem echten Spieler. c) Wie lang bzw. breit müsste ein Tipp-KickSpielfeld mindestens bzw. höchstens sein, sodass es im gleichen Maßstab verkleinert wurde wie eine Tipp-Kick-Spielfigur im Verhältnis zu einem 1,80 m großen Mann? Vergleiche mit den Angaben in Fig 1. 14 cm 21 a) Wie oft passt die Höhe einer Tipp- 40,32 m 34 cm 75 cm 45 – 90 m Fig. 1 22 a) Wie viele Gläser zu 0,2 Liter können Bei Aufgabe 22 c) kann es hilfreich sein, „eine Tabelle anzulegen“. mit dem Inhalt der Flasche gefüllt werden? b) Wie viel bekäme jeder, wenn der Flascheninhalt auf 8 Gläser verteilt wird? c) Wie viele 0,1-ø-; 0,2-ø-; 0,3-ø-; … Flaschen könnte man mit dem Inhalt füllen? Fig. 2 23 Für die Herstellung von Goldfolien werden Goldbarren ausgewalzt. Nun soll ein 4,5 cm langer, 3,4 cm breiter und 2,8 cm hoher Goldbarren zu einer rechteckigen Folie ausgewalzt werden. Die Folie ist 1,2 m lang und 75 cm breit. Wie dick ist die Folie geworden? 24 Ein Zimmer von 3,2 m Breite und 6,3 m Länge wird mit 0,5 cm dicken Korkplatten ausgelegt. Die Rechnung lautet: 20,16 kg Kork für Fußboden: 573,50 €. a) Wie viel kostet 1 m2 des Bodenbelages? b) Wie viel wiegt 1 m2 des Bodenbelages? 25 Jil möchte in ihrem Zimmer ein Aquarium aufstellen. Ihr Tisch, auf dem es aufgebaut werden soll, ist 1,8 m lang und 0,7 m breit. Jil möchte zudem, dass sich ihre Fische sehr wohl fühlen und liest daher in einem Fischbuch: „Für die Tiere eines Aquariums ist das Becken der Lebensraum. Für ein normales Becken verhält sich die Länge zur Breite und Höhe ungefähr im Verhältnis 10 : 5 : 6 bis 10 : 3 : 4. Die Zahl der Fische richtet sich nach dem Wasserinhalt des Beckens, also nicht nach dem errechneten Fassungsvermögen. Dabei muss das Volumen vom Bodengrund und Steinen abgezogen werden. Wer etwa anderthalb bis zwei Liter Wasser je Zentimeter Fisch rechnet, dürfte einigermaßen gut zurechtkommen.“ Ermittle mögliche Maße für Jils Aquarium. Lege dafür auch fest, welche und wie viele Fische in ihrem Aquarium leben sollen. 154 V Multiplikation und Division von rationalen Zahlen