- profi-L

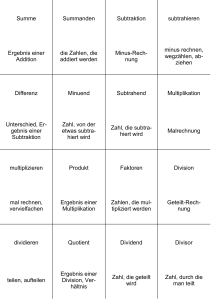
So dividiert man Brüche – oder so – oder so
Erklärungen und weitere Ideen zum Beitrag auf Seite 8/9
Die Botschaft wird vom Empfänger gemacht. Das gilt auch für Erklärungen. Die Lehrperson kann
noch so überzeugend formulieren – ob die Erklärung verstanden wird, entscheidet die/der
Lernende. Wenn sie nicht verstanden wird, sind Erklärungsvarianten immer von Vorteil.
Das im Beitrag vom Schüler vorgeschlagene Konzept „Brüche zum Dividieren gleichnamig
machen“ schliesst an die Division von Grössen an.
Die Frage, wie oft mal 75cm in 24km Platz haben, kann durch Gleichnamigmachen der beiden
Grössen und mit der Rechnung 24‘000m : 0.75m beantwortet werden: 32‘000 mal.
24 : 3 die Grössen „Fünfundzwanzigstel“ und „Viertel“
25 4
96 : 75 = 96 = 32 .
gleichnamig gemacht.
75
25
100 100
Entsprechend werden bei der Rechnung
Das Konzept, eine Division durch eine Multiplikation mit dem Kehrwert zu ersetzen, kann auf die
Einsicht abgestützt werden, dass Divisor und Quotient umgekehrt proportional sind, sowie auf der
Interpretation einer Division als Multiplikation mit einem Bruchteil.
24
24
24
24
:6
=4
:2
2
:3
=8
:2
2
: 1.5
= 16
:2
2
: 0.75
= 32
24 : 6 = 4
25
25
24  1 = 4
25 6 25
24 : 3 = 8
25
25
24  1 = 8
25 3 25
24 : 3 = 16
25 2 25
24  2 = 16
25 3 25
24 : 3 = 32
25 4 25
24  4 = 32
25 3 25
Der Divisor wird halbiert, der Quotient verdoppelt.
Die gleichen
Multiplikation
zweite Faktor
werden von
verdoppelt.
Rechnungen als
interpretiert. Der
und das Produkt
Zeile zu Zeile
Das Konzept „Zähler durch Zähler – Nenner durch Nenner“ basiert auf der Tatsache, dass die
Division die Umkehroperation zur Multiplikation ist.
Weil
24  4 = 24  4 = 96 ,
25 3 25  3 75
ist
96 : 4 = 96 : 4 = 24 .
75 3 75 : 3 25
Allenfalls muss vor dem Dividieren erweitert werden:
2 : 3 = 24 : 3 = 24 : 3 = 8 .
3 4
36 4
9
36 : 4