Vektorrechnung Ein Vektor ist eine gerichtete, orientierte Strecke im

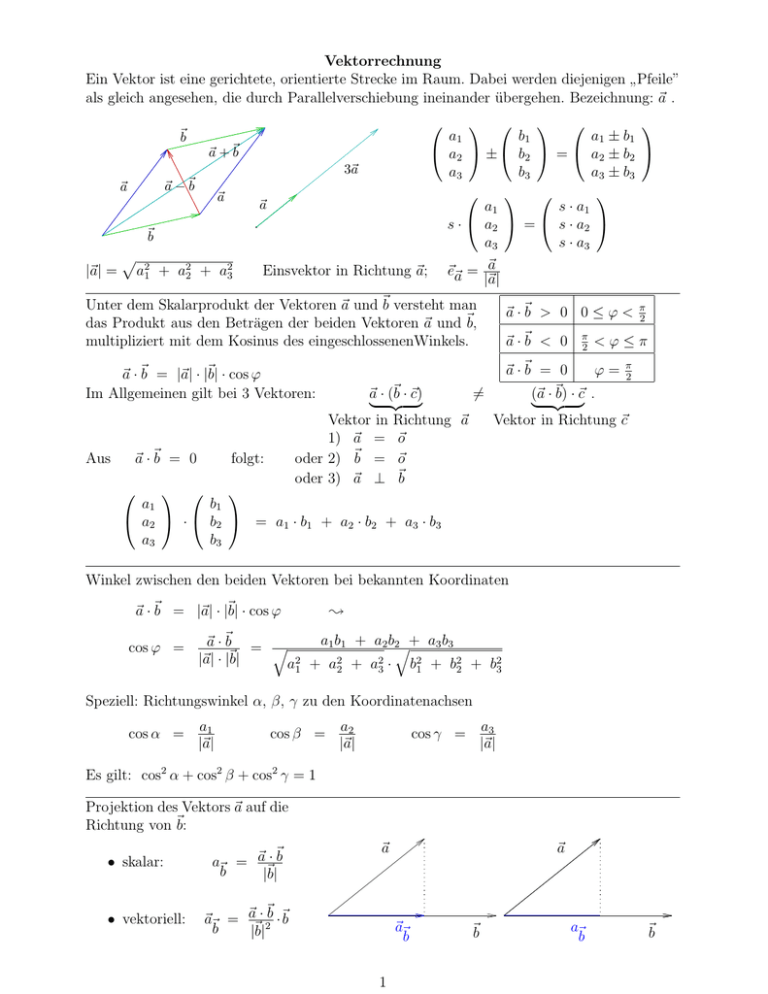
Vektorrechnung
Ein Vektor ist eine gerichtete, orientierte Strecke im Raum. Dabei werden diejenigen Pfeile”
”
als gleich angesehen, die durch Parallelverschiebung ineinander übergehen. Bezeichnung: ~a .

 
 

a1
b1
a1 ± b 1
 a2  ±  b 2  =  a2 ± b 2 
~a + ~b
3~a
a3
b3
a3 ± b 3
~
~a − b
~a

 

~a
~a
a1
s · a1
s ·  a2  =  s · a2 
~b
a3
s · a3
p
Einsvektor in Richtung ~a; ~e~a = ~a
|~a| = a21 + a22 + a23
|~a|
Unter dem Skalarprodukt der Vektoren ~a und ~b versteht man
~a · ~b > 0 0 ≤ ϕ < π2
~
das Produkt aus den Beträgen der beiden Vektoren ~a und b,
multipliziert mit dem Kosinus des eingeschlossenenWinkels.
~a · ~b < 0 π2 < ϕ ≤ π
~b
~a · ~b = 0
ϕ = π2
~a · (~b · ~c)
6=
(~a · ~b) · ~c .
| {z }
| {z }
Vektor in Richtung ~a
Vektor in Richtung ~c
1) ~a = ~o
oder 2) ~b = ~o
oder 3) ~a ⊥ ~b
~a · ~b = |~a| · |~b| · cos ϕ
Im Allgemeinen gilt bei 3 Vektoren:
Aus
~a · ~b = 0
folgt:

 
b1
a1
 a2  ·  b 2  = a1 · b 1 + a2 · b 2 + a3 · b 3
b3
a3

Winkel zwischen den beiden Vektoren bei bekannten Koordinaten
~a · ~b = |~a| · |~b| · cos ϕ
cos ϕ =
;
a1 b1 + a2 b2q+ a3 b3
~a · ~b = q
~
|~a| · |b|
a21 + a22 + a23 · b21 + b22 + b23
Speziell: Richtungswinkel α, β, γ zu den Koordinatenachsen
cos α =
a1
|~a|
cos β =
a2
|~a|
a3
|~a|
cos γ =
Es gilt: cos2 α + cos2 β + cos2 γ = 1
Projektion des Vektors ~a auf die
Richtung von ~b:
• skalar:
• vektoriell:
~
a~ = ~a · b
b
|~b|
~a
~
~a~ = ~a · 2b ·~b
~
b
|b|
~a
~a~
b
1
~b
a~
b
~b
Das mit ~a × ~b bezeichnete Vektorprodukt (Kreuzprodukt) steht senkrecht auf den Vektoren ~a und ~b , bildet
mit ~a, ~b in der Reihenfolge ~a , ~b , ~a ×~b ein Rechtssystem
und hat den Betrag
|~a × ~b| = |~a| · |~b| · | sin ϕ| ,
~a × ~b
~b
ϕ = ](~a, ~b) .
~a
~b
|~b| · sin ϕ
ϕ
~a
Der Betrag |~a × ~b| kann als die Maßzahl
der von den Vektoren ~a , ~b aufgespannten
Parallelogrammfläche gedeutet werden.
~a ⊥ ~b ; |~a × ~b| = |~a| · |~b|
Vekktorprodukt ist nicht kommutativ! ~a × ~b = −~b × ~a
Im Allgemeinen gilt für 3 Vektoren: ~a × (~b × ~c) 6= (~a × ~b) × ~c .
1) ~a = ~o
~
oder 2) ~b = ~o
Aus ~a × b = ~o
folgt
oder3) ~a k ~b .





a1
b1
a2 b 3 − a3 b 2
 a2  ×  b 2  =  a3 b 1 − a1 b 3 
oder Eselsbrücke“
”
a3
b3
a1 b2 − a2b1
~e1 ~e2 ~e3 a2 a3 − ~e2 · a1 a3
= a1 a2 a3 = ~e1 · b1 b3
b2 b3
b1 b2 b3 | {z }
| {z
a2 b3 −a3 b2
Spatprodukt
Wird das Vektorprodukt von zwei Vektoren ~b × ~c mit
dem Vektor ~a skalar multipliziert, so nennt man diese
Kombination Spatprodukt.
Schreibweise: [ ~a, ~b, ~c ] = ~a · (~b × ~c)
Das Spatprodukt lässt sich als (orientiertes) Volumen
des von den drei Vektoren aufgespannten Spats interpretieren.
mit ϕ = ](~a, ~b × ~c) .
~b × ~c
a1 b3 −a3 b1
+ ~e3 · a1 a2
b1 b2
}
| {z
a1 b2 −a2 b1
~a
h
ϕ
~c
Ap
~b
Die Eigenschaft [ ~a, ~b, ~c ] = 0 ist gleichwertig dazu, dass alle Vektoren in einer Ebene liegen.
Wird beim Spatprodukt die Reihenfolge der Vektoren verändert, so kann sich höchstens das
Vorzeichen ändern.
• Werden zwei Vektoren vertauscht (dritter Vektor bleibt auf seiner Position), so ändert
sich das Vorzeichen.
• Bei zyklischer Vertauschung“ bleibt das Vorzeichen erhalten.
” 
 

a1 a2 a3 a1
b2 c 3 − b3 c 2
~a · (~b × ~c) =  a2  ·  b3 c1 − b1 c3  = b1 b2 b3 c1 c2 c3 b1 c 2 − b2 c 1
a3
2
}
Gerade im Raum
g : ~x = ~x0 + λ~u (λ ∈ IR)
Punkt“ +
Richtung“
”
”
Durchläuft λ alle reellen Zahlen, so durchläuft ~x alle Punkte der Gerade.
Ebene in Parameterdarstellung
E:
~x = ~x0 + λ~u + µ~v
(λ, µ ∈ IR)
Punkt“ +
zwei Richtungen“
”
”
Durchlaufen λ, µ alle reellen Zahlen, so durchläuft ~x alle Punkte der Ebene.
Ebene; lineare Gleichung

 

x
n
1
1
~x = ~x0 + λ~u + µ~v | · ~n = ~u × ~v ;
 x2  ·  n2  = n1 · x1 + n2 · x2 + n3 · x3 = d
~n · ~x = ~n · ~x0 = d (= konstant )
x3
n3
(1 + λ) + 2λ + (1 − 2λ) = 3 ; λ = 1
Schnitt Ebene - Gerade
 




1
1
2
 


~s =  0  + 1 ·  1  =  1 
1
1
1
−2
−1
g : ~x =  0  + λ 1 
cos π2 − α = sin(α) = ~n · ~u
1
−2

  |~n|· |~u|
x1 = 1 + λ
1
1
x2 = λ
 1  · 2 
x3 = 1 − 2λ
−2
1
√ √
= 16
sin(α) =
E : x1 + 2x2 + x3 = 3
6· 6
E1 :
x1 + 2x2 + x3 = 3
Schnitt zweier Ebenen
E2 :
4x1 − x2 + 2x3 = 3
x1 = 1 − 5λ
x3 kann
1 2
1
1 2 1 3
3
x2 = 1 − 2λ
∼
;
frei gewählt
4 −1 2 3
0 −9 −2 −9
x3 =
9λ
werden!
 


1
−5
~x =  1  + λ −2  ( λ ∈ IR ) Schnittgerade
0
9
Schnittwinkel zweier Ebenen cos ϕ = ~n1 · ~n2
|~n1 | · |~n2 |
Abstand Punkt - Ebene
E : x1 + 2x2 + x3 = 3 ;

g⊥ :

1
~n =  2 
1



3
1



5
~x =
+ λ 2 
2
1

⇐⇒
P (3|5|2)
x1 = 3 + λ
x2 = 5 + 2λ
x3 = 2 + λ
(3 + λ) + 2(5 + 2λ) + (2 + λ) = 3 ; λ
 
 
 

3
1
1
~l =  5  − 2 2  =  1  ; LP
~ =
2
1
0
√
~ | = 2 6
; d = |LP
3
= −2


3
5  −
2
;
;

 
1
2


1
4 
=
0
2