Blatt 0

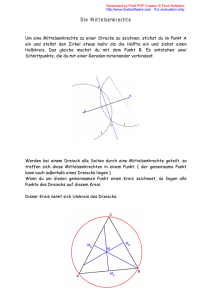
Prof. Dr. Felix Leinen
Geometrie, Algebra und Zahlentheorie“ im WS 15-16
”
23. Oktober 2015
ÜBlatt 0
Dieses Blatt soll in Ihrer ersten GAZ-Übungsstunde (2. Veranstaltungswoche) bearbeitet werden.
Bringen Sie hierzu einen Zirkel und ein maßstabloses Lineal mit.
1. Führen Sie, ausgehend von zwei verschiedenen Punkten in der Zeichenebene, die folgenden Konstruktionen mit Zirkel und Lineal im Stil der alten Griechen aus.
(a) Konstruktion eines allgemeinen Dreiecks“, das weder gleichschenklig noch rechtwinklig ist.
”
(b) Konstruktion des Umkreises Ihres allgemeinen Dreiecks.
(c) Konstruktion des Außendreiecks Ihres allgemeinen Dreiecks: die Seiten des Außendreiecks
sollen durch die Ecken Ihres allgemeinen Dreiecks verlaufen, parallel zur der jeweiligen Ecke
gegenberliegenden Seite Ihres allgemeinen Dreiecks.
(d) Welche speziellen Geraden Ihres allgemeinen Dreiecks sind zugleich die Mittelsenkrechten
des Außendreiecks ?
2. Wir betrachten ein vollkommen beliebiges Dreieck in der Zeichenebene. Weisen Sie nach, daß
(a) ..... alle drei Mittelsenkrechten des Dreiecks durch einen gemeinsamen Punkt verlaufen.
Welche Lage hat dieser Punkt in Bezug auf den Umkreis des Dreiecks?
(b) ..... alle drei Winkelhalbierenden des Dreiecks durch einen gemeinsamen Punkt verlaufen.
In Bezug auf welchen Kreis am Dreieck hat dieser Schnittpunkt eine ausgezeichnete Lage?
(c) ..... die drei Höhen des Dreiecks durch einen gemeinsamen Punkt verlaufen.
3. Imitieren Sie das Argument im Satz von Hippasos um zu
zeigen, daß Seite und Diagonale eines Quadrats in keinem
ganzzahligen Verhältnis zueinander stehen.
Dabei könnte die nebenstehende Skizze hilfreich sein.