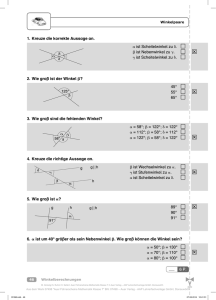
Lerninhalte selbst- ständig erarbeiten Mathematik 5

Download
Regina Nizold
Lerninhalte selbstständig erarbeiten
Mathematik 5
Figuren (Fläche, Umfang)
Sekund
arstufe
N
Regina
Lö
dig zum
s u n g sw
eg
albwert
ringe H
e
g
e
in
e
d
, haben
ken un
werden rufbar. Entdec
atheichtert
b
M
a
n
r
e
h
ht me
rientiert r verstanden
Zeit nic
etenzo
sse
s komp
e
iese be
in
d
e
n
e
e
nn
st, werd
lb
e
s
n
eranngege
blem h
eues Pro des wichtige
n
in
e
er an
Für je
iß, wie
andes.
ehrere
cht we
dieses B
u der m
n
z
e
,
rt
e
a
rt
ik
arten
a
e
k
rt
n
a
e
ip
K
b
T
a
ie
le pk
ine Aufg ll aus, wie vie
e
em
h
in
ic
e
s
s
ndet
bei in
dividue
eitet da
hlen in
e
ä
rb
d
a
w
n
r
r
e
e
le
h
d
ü
– je
ntsprec
r
langen
arten e
Zu jede
g zu ge
ie Tippk
d
ruppe.
g
n
rn
te
e
tellt,
L
ie
s
r
b
e
e
g
e
d
g
is
r
e
n
W
üle
gu
alle Sch arte zur Verfü
iten für
ungsk
s
ö
L
e
atheig die m en aus.
dem ein n kann.
e
stständ
nz
rd
lb
e
e
te
s
e
w
p
t
tt
ri
m
nutz
den Ko
für Sch
il
b
tt
ri
d
h
n
c
u
n
hüler S
trategie
sungss
ckeln Lö
gsstufe
Jahrgan
en der
m
e
h
T
tigen
en wich enkarte
ab
fg
u
A
r
e
de
benkart
a
fg
der Au
olische
Downloadauszug
aus dem Originaltitel:
schu
n für
llehreri
Mathe
matik
u n d Ka
th
I
izold
5
beiten
r
a
r
e
g
i
ständ
t
s
b
l
e
s
alte
Lerninh
k
i
t
a
m
e
h
t
a
M
chritt
für S
Schritt
n
e
t
r
a
k
p
Mit Tip
sung
igen Lö
t
h
ic
r
r
zu
Lerninhalte selbstständig erarbeiten
Mathematik 5
Figuren (Fläche, Umfang)
Dieser Download ist ein Auszug aus dem Originaltitel
Lerninhalte selbstständig erarbeiten Mathematik 5
Mit Tippkarten Schritt für Schritt zur richtigen Lösung
Über diesen Link gelangen Sie zur entsprechenden Produktseite im Web.
http://www.auer-verlag.de/go/dl7139
Figuren (Fläche, Umfang)
55
UMFANG DES QUADRATS
U=4·a
oder
U=a+a+a+a
Beim Quadrat sind alle
vier Seiten gleich lang!
Den Umfang eines Quadrats erhältst du, indem du eine Seitenlänge misst und diese
mal 4 nimmst.
2
b) Finde Beispiele für quadratische Formen im Klassenzimmer oder in der Schule.
UMFANG DES QUADRATS
U = 4 · 2 cm = 8 cm
U = 4 · 3 cm = 12 cm
b) Tafelseite, Bodenfliese, Stromkasten, zwei aneinandergelegte Geodreiecke, ...
a) Umfang Quadrat 1:
Umfang Quadrat 2:
UMFANG DES QUADRATS
Kopfumfang  Weite der Baseballkappe
Hasengehege  Länge des Maschendrahts
Bauchumfang  Länge des Gürtels
Folgende Beispiele sollen dir helfen:
Woher kennst du den Begriff „Umfang“?
1
M
us
A te
ns r
ic zu
ht r
a) Wie groß ist der Umfang (U) dieser Quadrate?
UMFANG DES QUADRATS
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
56 Figuren (Fläche, Umfang)
UMFANG DES RECHTECKS
Beim Rechteck sind jeweils
zwei Seiten gleich lang!
Rechteck 2: U = 2 · 3 cm + 2 · 1,5 cm = 6 cm + 3 cm = 9 cm
Rechteck 1: U = 2 · 2 cm + 2 · 1 cm = 4 cm + 2 cm = 6 cm
UMFANG DES RECHTECKS
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
U=2·a+2b
oder
U=a+b+a+b
UMFANG DES RECHTECKS
Der Umfang ist die Strecke, die die Maus zurücklegt, wenn sie einmal um das
Rechteck läuft.
1
M
us
A te
ns r
ic zu
ht r
Den Umfang eines Rechtecks erhältst du, indem du beide Seitenlängen misst und
diese mal 2 nimmst.
2
Berechne den Umfang (U) der Rechtecke.
UMFANG DES RECHTECKS
Figuren (Fläche, Umfang)
57
BEKANNTE FIGUREN ERKENNEN
Hier siehst du die jeweilige Idealfigur:
2
BEKANNTE FIGUREN ERKENNEN
Die vier Figuren Dreieck, Kreis, Parallelogramm und Rechteck haben sich jeweils
zweimal versteckt:
BEKANNTE FIGUREN ERKENNEN
Auch die letzte bekannte Figur hat jeweils gleich lange Seiten, die sich gegenüberliegen, aber nur in Ausnahmefällen rechte Winkel.
Bei der dritten Figur sind immer die gegenüberliegenden Seiten gleich. Auch sie hat
rechte Winkel.
Eine andere Figur hat vier gleich lange Seiten und nur rechte Winkel.
Eine Figur hat zwar keine Ecken, aber einen Mittelpunkt.
1
M
us
A te
ns r
ic zu
ht r
Hier haben sich vier bekannte Figuren mehrfach versteckt. Welche Figuren sind es?
Male sie an.
BEKANNTE FIGUREN ERKENNEN
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
58 Figuren (Fläche, Umfang)
RECHTECKE UND QUADRATE ZEICHNEN
b)
a)
c)
RECHTECKE UND QUADRATE ZEICHNEN
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Ein rechter Winkel
ist 90° groß!
RECHTECKE UND QUADRATE ZEICHNEN
Beim Quadrat sind alle
vier Seiten gleich lang!
Wenn nur ein Wert angegeben ist, musst du ein Quadrat zeichnen.
1
M
us
A te
ns r
ic zu
ht r
Quadrate und Rechtecke haben immer rechte Winkel. Du kannst sie ganz leicht anzeichnen, wenn du die Mittellinie deines Geodreiecks verwendest.
2
Benutze ein Geodreieck und einen Bleistift.
c) a = 4,5 cm
b) a = 4 cm; b = 3 cm
a) a = 3 cm
Zeichne Rechtecke oder Quadrate mit diesen Maßen:
RECHTECKE UND QUADRATE ZEICHNEN
Figuren (Fläche, Umfang)
59
TRAPEZ UND PARALLELOGRAMM VERVOLLSTÄNDIGEN
Zeichne erst die parallelen Linien ein.
2
b) ein Trapez:
a) ein Parallelogramm:
Vervollständige
TRAPEZ UND PARALLELOGRAMM VERVOLLSTÄNDIGEN
TRAPEZ UND PARALLELOGRAMM VERVOLLSTÄNDIGEN
b)
a)
Hier gibt es jeweils unterschiedliche Möglichkeiten!
TRAPEZ UND PARALLELOGRAMM VERVOLLSTÄNDIGEN
Bei einem Trapez müssen nur zwei Seiten parallel zueinander sein. Die Seiten
müssen nicht gleich lang sein.
Bei einem Parallelogramm sind die einander gegenüberliegenden Seiten jeweils
parallel und gleich lang.
1
M
us
A te
ns r
ic zu
ht r
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
60 Figuren (Fläche, Umfang)
PARALLEL ODER ORTHOGONAL?
a
b
c
e
d
Die Geraden e und d sowie b und c sind parallel.
b ist orthogonal zu f,
c ist orthogonal zu f.
PARALLEL ODER ORTHOGONAL?
Beispiel:
Parallele Linien haben an jeder Stelle den gleichen Abstand zueinander.
PARALLEL ODER ORTHOGONAL?
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Beispiel:
f
1
M
us
A te
ns r
ic zu
ht r
Orthogonale Linien stehen im rechten Winkel zueinander.
2
Überprüfe mit deinem Geodreieck,
welche Geraden parallel sind
und welche orthogonal.
PARALLEL ODER ORTHOGONAL?
Figuren (Fläche, Umfang)
61
2·a+2·b=?
Folgende Gleichung soll dir helfen:
Was kannst du mit a und b ausrechnen?
a = 3,50 m Länge
b = 3 m Breite
HOPPELS NEUES GEHEGE – WAS MUSS BERECHNET WERDEN?
Mache dir eine Skizze.
2
Wie viele Latten und Nägel muss Lea kaufen?
Außerdem braucht Lea noch Latten, an denen sie den Draht befestigen kann, und
Nägel. Für einen Meter Draht benötigt sie jeweils zwei Latten und vier Nägel.
Was muss sie berechnen?
Lea möchte das Gehege für ihren Hasen Hoppel neu einzäunen. Sie überlegt, wie viel
Meter Draht sie für das rechteckige Gehege besorgen muss, wenn es 3 m breit und
3,50 m lang ist.
HOPPELS NEUES GEHEGE – WAS MUSS BERECHNET WERDEN?
HOPPELS NEUES GEHEGE – WAS MUSS BERECHNET WERDEN?
Lea muss insgesamt 26 Latten und 52 Nägel kaufen.
4 Nägel · 13 m = 52 Nägel
2 Latten · 13 m = 26 Latten
Sie muss also 13 Meter Draht besorgen.
U = 2 · 3 m + 2 · 3,5 m = 6 m + 7 m = 13 m
Lea muss den Umfang (U) des Geheges berechnen.
HOPPELS NEUES GEHEGE – WAS MUSS BERECHNET WERDEN?
Notiere sie noch einmal gesondert.
Unterstreiche alle Angaben, die zum Berechnen des neuen Gehegezauns brauchst.
1
M
us
A te
ns r
ic zu
ht r
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
62 Figuren (Fläche, Umfang)
ZUSAMMENHANG ZWISCHEN UMFANG UND FLÄCHENINHALT
24 cm
12 cm
4 cm
2 cm
1 cm
1 cm
2 cm
6 cm
12 cm
24 cm
50 cm
28 cm
20 cm
28 cm
50 cm
Umfang
Je quadratischer seine Form ist, desto geringer wird der Umfang sein.
Der Umfang des Rechtecks ist dann am größten, wenn es lang und schmal ist.
ZUSAMMENHANG ZWISCHEN UMFANG UND FLÄCHENINHALT
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Querseite
Längsseite
Mögliche Tabelle:
Ordne die Rechtecke nach der Größe ihrer Längsseite, Querseite und ihrem Umfang.
Trage deine Ergebnisse in eine Tabelle ein.
2
Fällt dir etwas auf?
ZUSAMMENHANG ZWISCHEN UMFANG UND FLÄCHENINHALT
Mögliches Rechteck bestehend aus 24 Quadraten:
1
M
us
A te
ns r
ic zu
ht r
Schneide aus Kästchenpapier 24 Quadrate aus. Jedes Quadrat soll eine Seitenlänge
von 1 cm haben. Lege daraus alle möglichen Rechtecke.
Miss die Seiten der verschiedenen Rechtecke und berechne ihren Umfang.
ZUSAMMENHANG ZWISCHEN UMFANG UND FLÄCHENINHALT
Figuren (Fläche, Umfang)
63
GISELA GÄNSEBLÜMCHENS NEUES BEET (FLÄCHE AUFTEILEN)
Mögliche Beete in Rechteckform:
2
b) Wie viele Möglichkeiten hat sie höchstens, wenn
das Beet quadratisch werden soll?
a) Wie könnte das Beet aussehen? Finde verschiedene
Möglichkeiten.
Gisela Gänseblümchen will ein neues Beet anlegen. Sie will es
mit Fertigrasen bepflanzen. Ein Stück Fertigrasen ist 50 cm
m lang
und ebenso breit. Sie hat insgesamt 12 Stücke zur Verfügung.
gung.
Das Beet soll eine rechteckige Form haben.
GISELA GÄNSEBLÜMCHENS NEUES BEET (FLÄCHE AUFTEILEN)
GISELA GÄNSEBLÜMCHENS NEUES BEET (FLÄCHE AUFTEILEN)
b) Sie hat keine einzige Möglichkeit, da die Anzahl der Rasenstücke nicht zum
Quadrat gelegt werden kann.
Ein Beet von etwa gleicher Breite und Länge wäre 4 Stücke lang und 3 Stücke breit
oder umgekehrt.
4 · 50 cm = 200 cm Länge
3 · 50 cm = 150 cm Breite
a) Wenn sie ein ganz schmales Beet haben möchte, könnte sie den Fertigrasen zum
Beispiel 1 Stück breit auslegen. Das Beet wäre dann 6 Meter lang.
12 · 50 cm = 6 000 cm
GISELA GÄNSEBLÜMCHENS NEUES BEET (FLÄCHE AUFTEILEN)
Lege die Streifen in alle möglichen Rechtecke.
Mache eine Skizze oder schneide dir entsprechende Papierstreifen zurecht.
1
M
us
A te
ns r
ic zu
ht r
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
64 Figuren (Fläche, Umfang)
FLÄCHEN VERGLEICHEN
b)
a)
c) 16 cm2
b) 15 cm2
a) 12 cm2
Ermitteln der Lösung durch Auszählen der Quadratzentimeter:
FLÄCHEN VERGLEICHEN
Wichtig ist, dass diese Teile alle gleich groß sind.
Um die Flächengrößen miteinander zu vergleichen, kannst du sie in kleinere Teile
zerlegen.
FLÄCHEN VERGLEICHEN
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Zähle dann die Quadrate zusammen.
c)
1
M
us
A te
ns r
ic zu
ht r
Jedes Quadrat hat eine Seitenlänge von 1 cm und
eine Fläche von 1 cm2.
Teile alle Flächen in kleine Quadrate.
2
Welche Fläche
ist am größten?
FLÄCHEN VERGLEICHEN
Figuren (Fläche, Umfang)
65
WIE VIEL FARBE BRAUCHT DIE WAND? (FLÄCHEN BERECHNEN)
Dann zieht er die Türfläche von der Wandfläche ab:
A Wand – B Tür = Fläche, die zu streichen ist
Das Gleiche macht er mit der Tür:
B Tür = a ž b
Hausmeister Knauser berechnet zuerst die Wandfläche. Dazu multipliziert er die
Länge und die Breite:
A Wand = a ž b
2
b) Wie viel Farbe braucht er für die Fläche,
wenn er pro Quadratmeter 2 Liter Farbe benötigt?
a) Wie groß ist die Fläche, die Hausmeister Knauser
mit Farbe bestreichen soll?
Eine normale Tür hat
die Standardmaße
75 cm · 200 cm.
Er braucht 45 Liter Farbe.
b) 22,5 m2 · 2 l = 45 l
Die zu streichende Fläche ist 22,5 m2 groß.
A Wand – B Tür = 24 m2 – 1,5 m2 = 22,5 m2
B Tür = 0,75 m · 2 m = 1,5 m2
a) A Wand = 3 m · 8 m = 24 m2
WIE VIEL FARBE BRAUCHT DIE WAND? (FLÄCHEN BERECHNEN)
Sind alle Angaben vorhanden?
Die Wand ist 3 m hoch und 8 m lang.
In der Wand befindet sich eine Tür, die nicht mitgestrichen werden soll.
Mache eine Skizze.
WIE VIEL FARBE BRAUCHT DIE WAND? (FLÄCHEN BERECHNEN)
Unterstreiche alle Angaben, die du zur Berechnung der Wandfläche brauchst.
1
Hausmeister Knauser soll eine Wand in der Klasse 5a mit Magnetfarbe streichen,
damit die Schüler daran Bilder aufhängen können. Da die Farbe sehr teuer ist,
versucht er, möglichst genau zu berechnen, wie viel Farbe er für die Wand benötigt.
WIE VIEL FARBE BRAUCHT DIE WAND? (FLÄCHEN BERECHNEN)
M
us
A te
ns r
ic zu
ht r
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
66 Figuren (Fläche, Umfang)
f) einer CD-Hülle
e) einer Tischplatte
d) eines Baugrundstückes
c) eines Kartoffelackers
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Finde Beispiele.
?
1 ha
b) eines Kinderzimmers
a) eines Heftes
1 m2
1 dm2
Der Flächeninhalt
beträgt
WERTE UND EINHEITEN ZUORDNEN
Welche Einheiten sind eher klein, welche groß?
Welche Abmessungen haben
WERTE UND EINHEITEN ZUORDNEN
16,8 cm2.
f) einer CD-Hülle
2
1,6 m2.
etwa 6 dm2.
e) einer Tischplatte
d) eines Baugrundstückes
16 m2.
c) eines Kartoffelackers
beträgt
3 ha.
etwa 450 m2.
WERTE UND EINHEITEN ZUORDNEN
Sieh dir die Einheiten genau an.
1
M
us
A te
ns r
ic zu
ht r
b) eines Kinderzimmers
a) eines Heftes
Der Flächeninhalt
Hier sind die Zuordnungen durcheinandergeraten! Finde die richtigen Verbindungen.
WERTE UND EINHEITEN ZUORDNEN
16,8 cm2.
1,6 m2.
etwa 450 m2.
3 ha.
16 m2.
etwa 6 dm2.
Figuren (Fläche, Umfang)
67
10 m 10 m
Haus
WIE VIEL RASEN MÄHT LEON?
Reicht einmal Mähen für das Fahrrad?
Teile die errechnete Fläche durch 10 und multipliziere das Ergebnis mit seinem Lohn,
damit du weißt, was er für die gesamte Fläche bekommt.
Leon erhält für 10 m2 genau 10 Euro.
2
b) Wie oft muss er diese Rasenfläche mähen, bis er sich das neue Fahrrad für 400 €
kaufen kann?
a) Wie groß ist die Fläche, die Leon mähen muss?
30 m
WIE VIEL RASEN MÄHT LEON?
400 € : 50 € = 8
Um das Fahrrad kaufen zu können, muss Leon achtmal den Rasen mähen.
b) 500 m2 : 10 m2 = 5
5 · 10 € = 50 €
Leon erhält für einmal Mähen 50 €.
a) Rasenfläche A Rasen
20 m · 30 m = 600 m2
Hausfläche B Haus
10 m · 10 m = 100 m2
2
A – B = 500 m
Leon muss eine Fläche von 500 m2 mähen.
WIE VIEL RASEN MÄHT LEON?
Wie groß ist die Fläche des Hauses B Haus insgesamt?
Wie groß ist die Rasenfläche A Rasen insgesamt?
Beachte, dass er das Haus nicht mitberechnen darf.
Berechne zuerst, wie viel Rasen er mähen muss.
1
M
us
A te
ns r
ic zu
ht r
Leon will sein Taschengeld aufbessern, weil er sich ein neues Fahrrad wünscht.
Er bietet seinem Vater an, regelmäßig den Rasen zu mähen. Als Lohn möchte er
10 Euro für 10 Quadratmeter Rasen bekommen.
WIE VIEL RASEN MÄHT LEON?
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
20 m
68 Figuren (Fläche, Umfang)
WIE VIEL PLATZ HAT DAS BÜRO? (FLÄCHEN BERECHNEN)
b) 67 200 m2 : 2 000 = 33,6 m2
Jeder Angestellte hat 33,6 m2 Platz zur Verfügung.
a) 1 200 m2 · 56 = 67 200 m2
Die Büros haben alle zusammen eine Fläche von 67 200 m2.
WIE VIEL PLATZ HAT DAS BÜRO? (FLÄCHEN BERECHNEN)
Liste sie noch einmal gesondert auf.
Unterstreiche alle Angaben, die du zur Lösung der Aufgaben benötigst.
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
b) Bereche zuerst die Fläche, die alle Büros zusammen haben. Teile sie dann durch
die Anzahl der Angestellten.
a) Wenn 1 Stockwerk eine Fläche von 1 200 m2 hat, haben 56 Stockwerke eine Fläche
von ...
2
b) Wie viel Platz hat jeder Angestellte zur Verfügung,
wenn alle gleich viel Platz bekommen?
a) Wie viel m2 Fläche haben alle Büros zusammen?
WIE VIEL PLATZ HAT DAS BÜRO? (FLÄCHEN BERECHNEN)
Kläre unbekannte Begriffe.
1
M
us
A te
ns r
ic zu
ht r
Der Frankfurter Main Tower hat eine Höhe von 200 m.
Insgesamt gibt es 56 Geschosse über und fünf unter
der Erde. In jedem der oberirdischen Geschosse befinden
sich 1 200 m2 Bürofläche.
Im gesamten Gebäude arbeiten etwa 2 000 Menschen.
WIE VIEL PLATZ HAT DAS BÜRO? (FLÄCHEN BERECHNEN)
Figuren (Fläche, Umfang)
69
WIE LANG IST DIE AUSSENLINIE? (UMFANG BERECHNEN)
U=2ža+2žb
Zu b): Der Weg, den der Platzwart gehen muss, entspricht dem Umfang
des Spielfeldes.
2
b) Wie weit muss der Platzwart gehen, um die gesamte Außenlinie des Feldes
nachzuziehen?
a) Wie lang ist die kurze Linie des Spielfeldes?
Das Fußballfeld des FC Wursthausen hat eine Fläche von 7 140 m2. Der Platzwart
zieht regelmäßig die Außenlinie nach.
Die lange Seite des Spielfeldes misst 105 m.
WIE LANG IST DIE AUSSENLINIE? (UMFANG BERECHNEN)
WIE LANG IST DIE AUSSENLINIE? (UMFANG BERECHNEN)
Der Platzwart muss eine 346 m lange Außenlinie ziehen.
b) U = 2 ž 105 m + 2 ž 68 m = 210 m + 136 m = 346 m
Die kurze Linie des Spielfeldes ist 68 m lang.
a) 7 140 m2 : 105 m = 68 m
WIE LANG IST DIE AUSSENLINIE? (UMFANG BERECHNEN)
7 140 m2 = 105 m ž ?
A=ažbb=A:a
b=?
a = 105 m
A = 7 140 m2
Zu a): Berechne zuerst die kurze Linie des Spielfeldes.
1
M
us
A te
ns r
ic zu
ht r
Regina Nizold: Lerninhalte selbstständig erarbeiten Mathematik 5 © Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
M
us
A te
ns r
ic zu
ht r
Impressum
© 2013 Auer Verlag
AAP Lehrerfachverlage GmbH
Alle Rechte vorbehalten.
Das Werk als Ganzes sowie in seinen Teilen unterliegt dem deutschen Urheberrecht. Der Erwerber
des Werkes ist berechtigt, das Werk als Ganzes oder in seinen Teilen für den eigenen Gebrauch
und den Einsatz im Unterricht zu nutzen. Die Nutzung ist nur für den genannten Zweck gestattet,
nicht jedoch für einen weiteren kommerziellen Gebrauch, für die Weiterleitung an Dritte oder für
die Veröffentlichung im Internet oder in Intranets. Eine über den genannten Zweck hinausgehende
Nutzung bedarf in jedem Fall der vorherigen schriftlichen Zustimmung des Verlages.
Die AAP Lehrerfachverlage GmbH kann für die Inhalte externer Sites, die sie mittels eines Links
oder sonstiger Hinweise erreichen, keine Verantwortung übernehmen. Ferner haftet die AAP
Lehrerfachverlage GmbH nicht für direkte oder indirekte Schäden (inkl. entgangener Gewinne), die
auf Informationen zurückgeführt werden können, die auf diesen externen Websites stehen.
Autor: Regina Nizold
Illustrationen: Julia Flasche, Steffen Jähde, Stefan Leuchtenberg, Thorsten Trantow
www.auer-verlag.de