Angewandte Mathematik

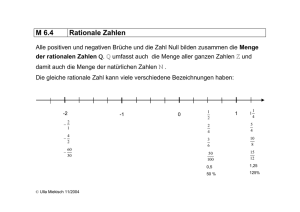
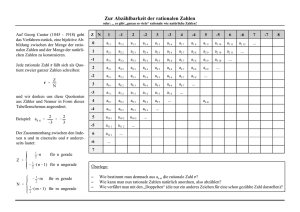
Angewandte Mathematik
Angewandte Mathematik
Ausgewählte Kapitel
Clemens Aigner, 2011
Clemens Aigner, 2011
Inhaltsverzeichnis
1
1.1
1.2
1.3
1.4
1.5
2
2.1
2.2
2.3
Folgen und Reihen, 9
Begriffe, 11
1.1.1
Folge, 11
1.1.2
Reihe, 11
Arithmetische Folge, 13
1.2.1
Definition, 13
1.2.2
Beispiel, 13
1.2.3
Berechnen von Zahlen der Folge, 13
Geometrische Folge, 15
1.3.1
Definition, 15
1.3.2
Beispiel, 15
1.3.3
Berechnen von Zahlen der Folge, 15
Arithmetische Reihe, 17
1.4.1
Definition, 17
1.4.2
Berechnung von Zahlen der Reihe, 17
Geometrische Reihe, 19
1.5.1
Definition, 19
1.5.2
Berechnung von Zahlen der Reihe, 19
1.5.3
Unendliche geometrische Reihe, 20
Rationale Zahlen, 23
Einleitung, Definitionen, 25
2.1.1
Definition „rationale Zahlen“, 25
2.1.2
Definition „irrationale Zahlen“, 25
2.1.3
Definition „reelle Zahlen“, 26
Reihenentwicklung, 27
2.2.1
Was bedeutet Reihenentwicklung?, 27
2.2.2
Zahlendarstellung mit Nennwerten, 27
2.2.3
Definition „periodische Zahlen“, 29
Periodische Zahlen, 31
2.3.1
Wiederholung, 31
2.3.2
Reihendarstellung rationaler Zahlen, 31
2.3.3
Zusammenfassung, 33
2.3.4
Periodische Zahlen im Zweiersystem, 33
5
Angewandte Mathematik - Ausgewählte Kapitel
3
3.1
3.2
3.3
6
Anhang, 37
Stichwortverzeichnis, 39
Abbildungsverzeichnis, 41
Konfiguration, 43
3.3.1
Dokumentversion, 43
3.3.2
Vorlagenversion, 43
3.3.3
History, 43
1
Folgen und Reihen
Clemens Aigner, 2011
1.1
1
Begriffe
Wir klären zuerst einmal Begriffe ab.
1.1.1
Folge
Definition
Eine Folge ist eine geordnete Menge von Zahlen.
Beispiel
1 3 12 8 6 9 0 -4 7
Hinweis
„Geordnet“ bedeutet bei einer Folge nicht, dass die Zahlen aus
dieser Menge selbst der Größe nach geordnet sind. „Geordnet“
bedeutet vielmehr, dass das erste Element dieser Menge von
Zahlen stets das erste ist, das zweite Element stets das zweite und
so weiter. Wir können diese Folge daher auch anders schreiben:
a0
a1
a2
a3
a4
a5
a6
a7
a8
1.1.2
=
=
=
=
=
=
=
=
=
1
3
12
8
6
9
0
-4
7
Reihe
Beispiel
Wir nehmen wieder unsere Folge von vorhin her.
1.1
Begriffe
11
1
Angewandte Mathematik - Ausgewählte Kapitel
a0
a1
a2
a3
a4
a5
a6
a7
a8
=
=
=
=
=
=
=
=
=
1
3
12
8
6
9
0
-4
7
Wir definieren nun eine weiter Folge aus Zahlen sn, die wie folgt
aus den Zahlen der obigen Folge gebildet wird:
s0
s1
s2
s3
s4
s5
=
=
=
=
=
=
a0
a0 +
a0 +
a0 +
a0 +
...
a1
a1 + a2
a1 + a2 + a3
a1 + a2 + a3 + a4
s0
s1
s2
s3
s4
=
=
=
=
=
1
1
1
1
1
+
+
+
+
3
3
3
3
=
+
+
+
4
12 = 16
12 + 8 = 24
12 + 8 + 6 = 30
Wir haben durch diese systematische Summierung von Zahlen
einer Folge an eine weitere Folge sn gebildet.
Eine Folge, die durch eine solche Aufsummierung von
Folgengliedern entsteht, wird auch als Reihe bezeichnet.
Die Zahl, die durch Aufsummierung einer bestimmten Anzahl von
Zahlen einer Folge entsteht, wird als Partialsumme dieser Folge
bezeichnet.
Eine konkrete Zahl einer Reihe ist gleich der entsprechenden
Partialsumme der zugehörigen Folge.
Definition
Eine Reihe ist eine Folge, die aus den Partialsummen einer
bestimmten Folge besteht.
12
1
Folgen und Reihen
Clemens Aigner, 2011
1.2
1
Arithmetische Folge
Unsere erste spezielle Folge.
1.2.1
Definition
Eine arithmetische Folge ist eine Folge, bei der aufeinander
folgende Zahlen dieser Folge stets jeweils die gleiche Differenz
zueinander haben.
1.2.2
Beispiel
a0
a1
a2
a3
a4
=
=
=
=
=
5
8
11
14
17
Die Differenz zweier aufeinander folgender Zahlenwerte in dieser
Folge ist also offensichtlich hier 3.
1.2.3
Berechnen von Zahlen der Folge
Im Prinzip kann man sich hier jeden vorhandenen Zahlenwert einer
Folge ausrechnen, wenn man neben der Differenz von jeweils zwei
Zahlen dieser Folge auch zum Beispiel die erste Zahl dieser Folge
weiß.
Die soeben gezeigte Folge lässt sich also so eindeutig definieren:
a0 = 5
d = 3
a0 ist hierbei die erste Zahl der Folge, d die Differenz von jeweils
zwei aufeinander folgenden Zahlen in dieser Folge.
1.2
Arithmetische Folge
13
1
Angewandte Mathematik - Ausgewählte Kapitel
Wenn eine arithmetische Folge durch a0 und d definiert ist, so
lassen sich alle weiteren Zahlen an dieser Folge wie folgt
ausrechnen:
an = a0 + n * d
14
1
Folgen und Reihen
Clemens Aigner, 2011
1.3
1
Geometrische Folge
Noch eine spezielle Folge
1.3.1
Definition
Eine geometrische Folge ist eine Folge, bei der aufeinander
folgende Zahlen dieser Folge stets jeweils den gleichen Quotienten
zueinander haben.
1.3.2
Beispiel
b0
b1
b2
b3
b4
=
=
=
=
=
2
-6
18
-54
162
Der Quotient zweier aufeinander folgender Zahlenwerte in dieser
Folge ist also offensichtlich hier -3.
1.3.3
Berechnen von Zahlen der Folge
Im Prinzip kann man sich hier jeden vorhandenen Zahlenwert
dieser Folge ausrechnen, wenn man neben dem Quotienten von
jeweils zwei Zahlen dieser Folgen auch zum Beispiel die erste Zahl
dieser Folge weiß.
Die soeben gezeigte Folge lässt sich also so eindeutig definieren:
b0 = 2
q = -3
b0 ist hierbei die erste Zahl der Folge, q der Quotient von jeweils
zwei aufeinander folgenden Zahlen in dieser Folge.
1.3
Geometrische Folge
15
1
Angewandte Mathematik - Ausgewählte Kapitel
Wenn eine geometrische Folge durch b0 und q definiert ist, so
lassen sich alle weiteren Zahlen bn dieser Folge wie folgt
ausrechnen:
bn = b0 * qn
16
1
Folgen und Reihen
Clemens Aigner, 2011
1.4
1
Arithmetische Reihe
Zur arithmetischen Folge gibt es auch eine arithmetische Reihe.
1.4.1
Definition
Eine arithmetische Reihe ist die auf eine arithmetische Folge
aufbauende Reihe.
1.4.2
Berechnung von Zahlen der Reihe
Zur Berechnung von Zahlen der Reihe greifen wir auf die
Berechnungsformel für eine allgemeine Zahl der Folge zurück. Für
diese allgemeine Zahl an der Folge gilt.
an = a0 + n * d
Wir wollen nun eine Formel zur Bestimmung der Zahlen sn der
Reihe finden, wenn a0 und d bekannt sind.
s0 = a0
s1 = a0 + a1 =
= a0 + a0 + d =
= 2 * a0 + d
s2 = a0 + a1 + a2 =
= a0 + a0 + d + a0 + 2 * d =
= 3 * a0 + 3 * d
s3 = a0 + a1 + a2 + a3 =
= a0 + a0 + d + a0 + 2 * d + a0 + 3 * d =
= 4 * a0 + 6 * d
Wir sehen hier eine gewisse Systematik, können aber noch keine
allgemein gültige Formel aufstellen. Wir probieren daher einen
anderen Weg.
Auf jeden Fall gilt (so wurde ja definiert):
sn = a0 + a1 + a2 + ... + an-2 + an-1 + an
1.4
Arithmetische Reihe
17
1
Angewandte Mathematik - Ausgewählte Kapitel
Wir multiplizieren mit 2, die rechte Seite der Gleichung schreiben
wir aber als Addition mit sich selbst:
2 * sn = a0 + a1 + a2 + ... + an-2 + an-1 + an +
+ a0 + a1 + a2 + ... + an-2 + an-1 + an
Nun ordnen wir die in der zweiten Zeile der Formel stehenden
Zahlen genau umgekehrt an:
2 * sn = a0 + a1 + a2 + ... + an-2 + an-1 + an +
+ an + an-1 + an-2 + ... + a2 + a1 + a0
Wir betrachten nun jeweils zwei genau untereinander stehende
Zahlen. Konkret kann man ja sagen, dass jeweils die Zahl ai und
die Zahl an-i untereinander steht. Es gilt:
ai = a0 + i * d
Ebenso gilt
an-i = a0 + (n – i) * d
Die Summe der beiden Zahlen ist ...
ai + an-i = a0 + i * d + a0 + (n – i) * d = 2 * a0 + n * d
... und damit von i unabhängig.
Insgesamt gibt es n + 1 „Paare“ von Zahlen untereinander stehen,
die aufsummiert werden. Es gilt daher:
2 * sn = (n + 1 ) * (2 * a0 + n * d)
Die allgemeine Zahl einer arithmetischen Reihe ergibt sich somit
aus a0 und d der dazu gehörenden Folge zu:
sn = ((n + 1) / 2) * (2 * a0 + n * d)
18
1
Folgen und Reihen
Clemens Aigner, 2011
1.5
1
Geometrische Reihe
Nun das selbe in „geometrisch“: Zur geometrischen Folge gibt es
auch eine geometrische Reihe.
1.5.1
Definition
Eine geometrische Reihe ist die auf eine geometrische Folge
aufbauende Reihe.
1.5.2
Berechnung von Zahlen der Reihe
Zur Berechnung von Zahlen der Reihe greifen wir auf die
Berechnungsformel für eine allgemeine Zahl der Folge zurück. Für
diese allgemeine Zahl an der Folge gilt.
bn = b0 * qn
Es gilt (nach der Definition einer Reihe):
sn = b0 + b1 + b2 + ... + bn-1 + bn
Anders aufgeschrieben (nur mehr mit b0 und q):
sn = b0 + b0 * q + b0 * q2 + ... + b0 * qn-1 + b0 * qn
Herausheben:
sn = b0 * (1 + q + q2 + ... + qn-1 + qn)
[I]
Das sei die Gleichung [I]. Nun bilden wir eine zweite Gleichung
[II], indem wir diese Gleichung mit q multiplizieren.
q * sn = b0 * (q + q2 + q3 ... + qn + qn+1)
[II]
Wir schreiben jetzt Gleichung [I] und Gleichung [II]
untereinander, und zwar so, dass immer die gleichen Potenzen von
q untereinander stehen:
sn = b0 * (1 + q + q2 + q3.+ ... + qn)
q * sn = b0 * (
q + q2 + q3 + ... + qn + qn+1)
1.5
Geometrische Reihe
[I]
[II]
19
1
Angewandte Mathematik - Ausgewählte Kapitel
Nun bilden wir die Differenz, wir subtrahieren die Gleichung [II]
von der Gleichung [I]:
sn * (1 – q) = b0 * (1 – qn+1)
Wir sehen, dass sich hier sehr viele Zahlen bei der Subtraktion
gegenseitig aufheben, und so können wir nach einfacher
Umformung das Ergebnis schreiben:
sn = b0 * (1 – qn+1) / (1 - q)
1.5.3
Unendliche geometrische Reihe
Es gibt geometrische Folgen, die unendlich viele Elemente haben.
Genauer gesagt kann das ja jede Folge sein, da sich jedes
beliebige Element bn mit noch so großem Index n ja aus b0 und q
errechnen lässt.
bn = b0 * qn
Diese Formel kennen wir ja bereits.
Nun lassen wir den Index n immer größer werden, also gegen
unendlich gehen.
Es lässt sich zeigen, dass hierbei bei immer größer werdenden n
die Werte von sn genau dann stets endlich bleiben, wenn der
Betrag von q kleiner als 1 ist.
Die geometrische Reihe nähert sich dabei in mathematischem Sinn
einem Grenzwert. Dieser Grenzwert lässt sich einfach angeben,
indem wir unsere Formel für die endliche geometrische Reihe
hernehmen ...
sn = b0 * (1 – qn+1) / (1 - q)
... und darin n gegen unendlich gehen lassen. Für ein q mit Betrag
kleiner als 1 gilt, dass qn (und damit auch qn+1) gegen 0 geht, wenn
n gegen unendlich geht.
Es gilt also:
s = b0 / (1 – q)
Das ist die Summe einer unendlichen geometrischen Folge mit
Anfangswert b0 und Quotient q, wobei q dem Betrag nach kleiner
als 1 sein muss.
20
1
Folgen und Reihen
2
Rationale Zahlen
Clemens Aigner, 2011
2.1
2
Einleitung, Definitionen
Um welche Zahlen geht es?
2.1.1
Definition „rationale Zahlen“
Definition, Formulierung 1
Eine rationale Zahl ist eine Zahl, die sich als Quotient von zwei
ganzen Zahlen darstellen lässt.
Definition, Formulierung 2
Eine rationale Zahl ist eine Zahl, zu der es mindestens eine ganze
Zahl gibt, sodass das Produkt aus diesen beiden Zahlen ganzzahlig
wird.
Hinweis
Ganze Zahlen (also Zahlen ohne Kommastellen) sind stets auch
rationale Zahlen. Die Menge der ganzen Zahlen ist eine Teilmenge
der rationalen Zahlen.
2.1.2
Definition „irrationale Zahlen“
Definition, Formulierung 1
Irrationale Zahlen sind Zahlen, die nicht als Quotient zweier ganzer
Zahlen dargestellt werden können.
Definition, Formulierung 2
Eine irrationale Zahl ist eine Zahl, für die es keine einzige ganze
Zahl gibt, sodass das Produkt aus diesen beiden Zahlen ganzzahlig
wird.
2.1
Einleitung, Definitionen
25
2
Angewandte Mathematik - Ausgewählte Kapitel
2.1.3
Definition „reelle Zahlen“
Die Menge der reellen Zahlen ist die Vereinigungsmenge der
Menge der rationalen Zahlen mit der Menge der irrationalen
Zahlen.
26
2
Rationale Zahlen
Clemens Aigner, 2011
2.2
2
Reihenentwicklung
Wir lernen nun eine spezielle, wenngleich auch durchaus
gebräuchliche Darstellung von reellen Zahlen kennen.
2.2.1
Was bedeutet Reihenentwicklung?
Für jede reelle Zahl existieren Reihenentwicklungen.
Die Reihenentwicklung einer Zahl bedeutet die Angabe einer Folge
von Zahlen, deren Summe exakt gleich der gleich der zu
entwickelnden Zahl ist.
Diese Folge von Zahlen hat nicht immer eine endliche Länge,
besteht also nicht immer aus endlich vielen Zahlen. In vielen Fällen
ist die Folge von Zahlen, deren Summe gleich der zu
entwickelnden Zahl ist, unendlich lang, besteht also aus unendlich
vielen Elementen.
2.2.2
Zahlendarstellung mit Nennwerten
Die Darstellung einer reellen Zahl mit Hilfe von Nennwerten ist
eine spezielle Reihenentwicklung einer reellen Zahl.
Die reelle Zahl wird als Summe von rationalen Zahlen dargestellt.
Der Nenner jeder dieser rationalen Zahlen ist jeweils ein
Stellenwert der Darstellung im jeweiligen Zahlensystem.
Beispiel 1
Gegeben ist die rationale Zahl Zahl 3/8. Reihenentwicklung dieser
Zahl wird durch Ausführen der Division erstellt. Konkret wird hier
in diesem Beispiel das Zehnersystem verwendet.
2.2
Reihenentwicklung
27
2
Angewandte Mathematik - Ausgewählte Kapitel
3 : 8 = 0,375
30
60
40
0
Die Zahl 3/8 lässt sich also so schreiben:
3
3
7
5
= 1  2 3
8 10 10 10
Beispiel 2
Gegeben ist die rationale Zahl 2/3. Die Dezimalbruchentwicklung
dieser Zahl wird durch Ausführen der Division erstellt, auch hier
kommt wieder das Zehnersystem zum Einsatz.
2 : 3 = 0,66
20
20
2
Wir sehen hier, dass wir offensichtlich unendlich viele Stellen rechts
vom Komma benötigen, um diese Zahl exakt darzustellen. Wir
schreiben für die Zahl 2/3 also:
2
6
6
6
=


...
3 101 102 103
Durch die abschließenden Punkte soll hier angezeigt werden, dass
es sich hierbei um eine Reihe aus unendliche vielen Zahlen
handelt. Die gleichen Punkte können wir auch so schreiben:
2/3 = 0,666...
Beide Schreibweisen mit den Punkten sind aber unschön. Konkret
wird ja nur ausgesagt, dass hier noch etwas fehlt, es wird aber
nicht ausgesagt, was denn hier eigentlich fehlt.
Aus diesem Grund hat sich eine andere Schreibweise eingebürgert.
Wir schreiben nur den ersten der unendlich vielen gleichen
Zahlenwerte (Nennwerte), und machen einen Strich darüber:
2/3 = 0,6
Beispiel 3
Wir betrachten den gleichen Sachverhalt mit der rationalen Zahl
5/7.
5 : 7 = 0,714285
50
10
30
20
60
40
5
Wir sehen hier erst nach einigen Divisionsschritten, dass wieder
der gleiche Rest wie schon zuvor einmal auftritt. Aus rechnerischen
Gründen wiederholt sich daher die Zahlenfolge ab diesem
Zeitpunkt immer wieder:
28
2
Rationale Zahlen
Clemens Aigner, 2011
2
5/7 = 0, 714285 714285 714285 ...
Auch hier schreiben wir wieder mit einem Strich darüber:
5/7 = 0,714285
Beispiel 4
Wir betrachten nun den gleichen Sachverhalt mit der rationalen
Zahl 82/300.
82 : 300 = 0,2733
820
2200
1000
1000
100
Nun sehen wir, dass nach einigen Schritten stets der gleiche Rest
auftritt, was natürlich dazu führt, dass ab dieser Stelle auch stets
der gleiche Nennwert auftritt. Wir schreiben die Zahl daher so:
82/300 = 0,273
Der Strich über dem letzten Nennwert bedeutet, dass sich ab da
genau dieser Nennwert wiederholt.
Beispiel 5
Nun nehmen wir eine irrationale Zahl her, konkret die Wurzel aus 3
(√3). Wir rechnen wieder:
√3 = 1,73205
200 : 27
1100 : 343
07100 : 3462
017600 : 34640
1760000 : 346405
027975
Wir können wieder mit unseren Punkten arbeiten:
√3 = 1,73205...
 3=1
7
10
1

3
10
2

2
3
10

0
10
4

5
10
5
...
Unsere Darstellung mit dem Strich über den Zahlen können wir
aber vergessen. Wir wissen nämlich nicht, ob sich hier eine
Zahlenfolge wiederholt
Das wussten wir nur bei den Beispielen mit den rationalen Zahlen.
Dort hat das Auftreten eines Divisionsrests, der schon vorher
einmal aufgetreten ist, automatisch gleiche Nennwerte wie zuvor
erzwungen.
2.2.3
Definition „periodische Zahlen“
Begriff
Wir bezeichnen reelle Zahlen als periodisch, wenn ihre
Reihenentwicklung mit Hilfe von Stellenwerten eines
Zahlensystems ein wiederkehrendes Muster erzeugt.
2.2
Reihenentwicklung
29
2
Angewandte Mathematik - Ausgewählte Kapitel
Rationale Zahlen und Periodizität
Rationale Zahlen sind stets periodische Zahlen.
Beweis
Der Beweis dafür wurde schon begonnen:
• Wir wissen ja, dass eine Periode dadurch entsteht, dass bei der
Division ein Rest auftritt, der bereits vorher schon einmal
aufgetreten ist.
Das ist aber noch kein Beweis, dass ein Rest wiederholt auftritt. Es
ist aber tatsächlich so, und zwar aus folgendem Grund:
• Bei einer Division durch eine Zahl n können nur Reste im
Bereich von 0 bis n-1 auftreten. Es gibt also n verschiedene
Reste. Und damit muss spätestens nach n Schritten ein Rest
auftreten, der vorher schon einmal aufgetreten ist.
Hinweis
Wenn bei der Division der Rest 0 auftritt, sind (auf Grund der
Rechenregeln der Division) alle weiteren Nennwerte gleich 0. Die
Zahl hat also endlich viele (von 0 verschiedene) Stellen und ist
daher auf den ersten Blick keine periodische Zahl.
Auf den zweiten Blick sieht die Sache anders aus. Eine Zahl mit
endlich vielen Stellen kann als periodische Zahl angesehen werden,
wobei die Periode aus der Zahl 0 besteht. Beispiel:
3/8 = 0,375 = 0,3750
In diesem Sinne kann also mit Sicherheit gesagt werden, dass jede
rationale Zahl eine periodische Zahl ist. Umgekehrt ist auch jede
periodische Zahl automatisch eine rationale Zahl.
Irrationale Zahlen und Periodizität
Es sei ohne Beweis angegeben, dass irrationale Zahlen niemals
periodische Zahlen sind.
30
2
Rationale Zahlen
Clemens Aigner, 2011
2.3
2
Periodische Zahlen
Wir wollen nun periodische (also rationale) Zahlen näher
beleuchten.
Unser Ziel ist es, aus der Kenntnis der Reihenentwicklung einer
rationalen Zahl (mit oder ohne Periode) auf die Darstellung als
Bruch ganzer Zahlen zu schließen.
2.3.1
Wiederholung
Entwicklung reeller Zahlen
Wir haben schon festgestellt, dass alle reellen Zahlen (also sowohl
die rationalen als auch die irrationalen Zahlen) stets in eine Reihe
aus rationalen Zahlen entwickelt werden können.
• Eine spezielle Reihenentwicklung ist dabei die, bei der die
Nenner der Zahlen der Reihe die Potenzen der Basis eines
Zahlensystems sind. Wir haben uns bisher auf diese eine
Reihenentwicklung beschränkt und werden das auch weiter tun.
Entwicklung rationaler Zahlen
Dies Reihen, die rationale, also periodische Zahlen darstellen,
haben noch eine weitere Eigenschaft, nämlich:
• Die Zähler der auftretenden Zahlen der Reihe kehren nach
einem periodischen Muster wieder.
2.3.2
Reihendarstellung rationaler Zahlen
Beispiel 1
Wir nehmen einmal eine ganz einfache periodische Zahl z her:
z = 0,3
Oder, anders geschrieben:
2.3
Periodische Zahlen
31
2
Angewandte Mathematik - Ausgewählte Kapitel
z=
3
10
1

3
10
2

3
10
3

3
10
4

3
10
5
...
Wir sehen hier eine unendliche geometrische Reihe. Eine
unendliche geometrische Reihe ist durch ihren Anfangswert b0 und
durch den Quotienten von zwei aufeinander folgenden Werten q
bestimmt.
Für unseren Fall gilt:
b1 = 3/10
q = 1/10
Es gilt daher:
3
3
10
10 3 1
z=
=
=
= =
1−q
1
9 9 3
1−
10 10
b1
Wir haben hier also mit der Formel für die unendliche geometrische
Reihe die Reihendarstellung einer rationalen Zahl in die
Bruchdarstellung umgewandelt.
Beispiel 2
Wir nehmen einmal eine ganz einfache periodische Zahl z her:
z = 0,27
Oder, anders geschrieben:
z=
2
10
1

7
10
2

2
10
3

7
10
4

2
10
5

7
10
6
...
Bruchdarstellung - Möglichkeit 1
Eine Möglichkeit, hier eine Bruchdarstellung für z zu gewinnen, ist,
hier zwei Reihen z1 und z2 zu sehen, wobei z = z1 + z2 gilt.
z 1=
z 2=
2
10
1

2

7
10
2
10
3

4

7
10
2
10
5
...
6
...
7
10
Berechnung von z1 - es gilt:
b11= 2/10
q1 = 1/100
2
2
10
10 20
z 1=
=
=
=
1−q 1
1
99 99
1−
100 100
b 11
Berechnung von z2 - es gilt:
b12= 7/100
q2 = 1/100
7
7
100
100 7
z 2=
=
=
=
1−q 2
1
99 99
1−
100 100
b 12
Berechnung von z:
32
2
Rationale Zahlen
Clemens Aigner, 2011
z=z 1 z 2=
2
20 7 27
 =
99 99 99
Bruchdarstellung - Möglichkeit 2
z=
2
10
1

7
10
2

2
10
3

7
10
4

2
10
5
7

10
6
...
Wir fassen jeweils 2 Terme zusammen:
z=
2
10
1

7
10
2

2
3

1

10
7
10
4

2
⋅
2
10
5

7
6
10
...
Herausheben:
z=
2
10
1

7
10
2

2
10
7
10
1
2
10

2
10
1

7
10
2
⋅
1
10
4
...
Noch einmal herausheben:
z=
2
10
1

7
10
2
⋅1
1
10
2

1
10
4
...
Wir erkennen daher:
b1= 2/10 + 7/100 = 27/100
q = 1/100
Berechnung von z:
27
27
100
100 27
z=
=
=
=
1−q
1
99 99
1−
100 100
b1
2.3.3
Zusammenfassung
Mit den Regeln für die unendliche geometrische Reihe ist es
möglich, eine periodische (rationale) Zahl, die in einer
Reihendarstellung vorliegt, als Bruchzahl darzustellen.
Die Methode dazu ist, aus der Reihendarstellung eine unendliche
geometrische Reihe herauszulösen und auf diese dann die
Summenformel anzuwenden.
2.3.4
Periodische Zahlen im Zweiersystem
Der soeben gezeigte Zusammenhang zwischen der
Reihendarstellung einer periodischen Zahl und ihrer Darstellung als
Bruchzahl gilt natürlich für alle Zahlensysteme. Im Speziellen gilt
er auch für das Zweiersystem.
Als Beispiel dazu wollen wir eine im Zweiersystem dargestellte
periodische Zahl als Bruchzahl aus ganzen, im Zehnersystem
dargestellten Zahlen darstellen.
Gegeben sei die im Zweiersystem dargestellte periodische Zahl z.
z = 0,1001
z=
1
1
2

0
2
2

0
2
3

1
2
4

1
5
2
...=
1
2
1

1
4
2

1
5
2
2.3

1
8
2

1
2
9

1
2
12
...
Periodische Zahlen
33
2
Angewandte Mathematik - Ausgewählte Kapitel
Herausheben, so wie vorhin:
z=
1
2
1

1
4
2
⋅1
1
4
2

1
8
2

1
12
2
...
Wir erkennen :
b1= 1/2 + 1/16 = 9/16
q = 1/16
Berechnung von z:
9
9
16
16 9 3
z=
=
=
=
=
1−q
1
15 15 5
1−
16 16
b1
Man beachte, dass die ganze Rechnung im Zehnersystem
ausgeführt wurde und das Ergebnis daher klarerweise bereits im
Zehnersystem dargestellt ist.
34
2
Rationale Zahlen
3
Anhang
Clemens Aigner, 2011
3.1
3
Stichwortverzeichnis
3.1
Stichwortverzeichnis
39
Clemens Aigner, 2011
3.2
3
Abbildungsverzeichnis
3.2
Abbildungsverzeichnis
41
Clemens Aigner, 2011
3.3
3
Konfiguration
Vorlagenversion, Dokumentversion
3.3.1
Dokumentversion
Version 1.0 - 15.2.2011
3.3.2
Vorlagenversion
Version 1.7 - 2.2.2011
3.3.3
History
Version 1.0 – 15.2.2011
Erstentwurf
3.3
Konfiguration
43