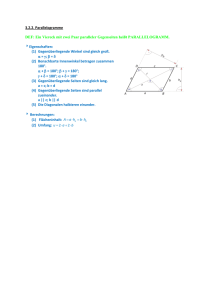
Die Höhen schneiden einander im Höhenschnittpunkt H. Der

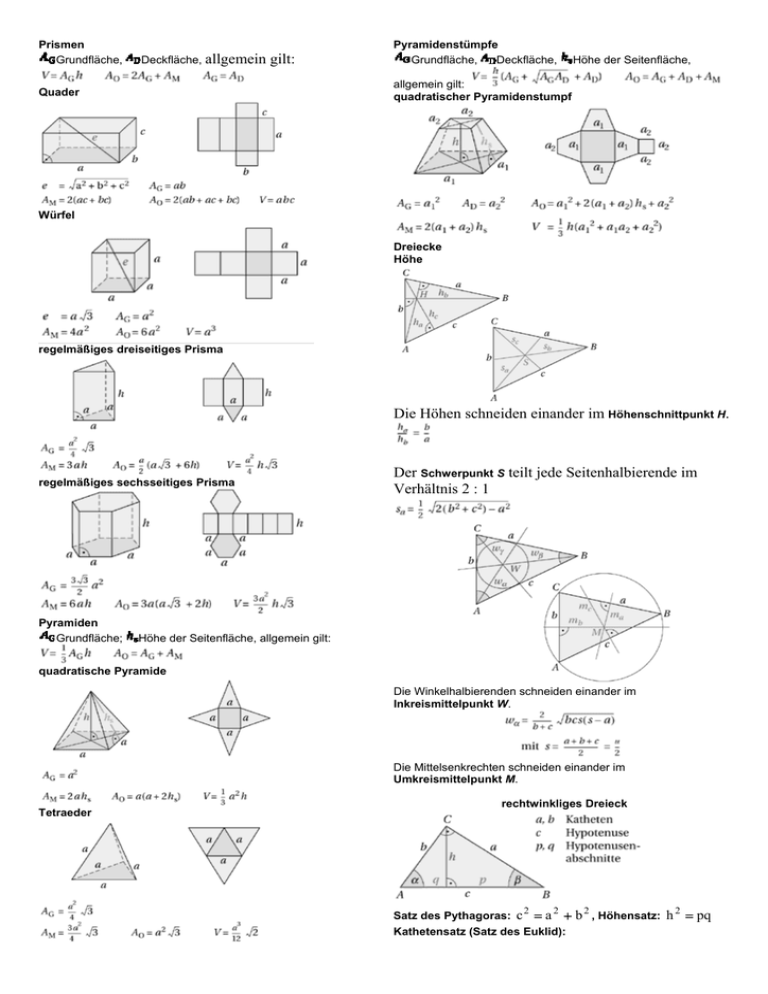
Prismen
Grundfläche,
Deckfläche, allgemein
gilt:
Pyramidenstümpfe
Grundfläche,
Deckfläche,
Höhe der Seitenfläche,
allgemein gilt:
quadratischer Pyramidenstumpf
Quader
Würfel
Dreiecke
Höhe
regelmäßiges dreiseitiges Prisma
Die Höhen schneiden einander im Höhenschnittpunkt H.
regelmäßiges sechsseitiges Prisma
Pyramiden
Grundfläche;
Der Schwerpunkt S teilt jede Seitenhalbierende im
Verhältnis 2 : 1
Höhe der Seitenfläche, allgemein gilt:
quadratische Pyramide
Die Winkelhalbierenden schneiden einander im
Inkreismittelpunkt W.
Die Mittelsenkrechten schneiden einander im
Umkreismittelpunkt M.
Tetraeder
rechtwinkliges Dreieck
Satz des Pythagoras: c = a +
Kathetensatz (Satz des Euklid):
2
2
b 2 , Höhensatz: h 2 = pq
Trapez
gleichseitiges Dreieck
Mindestens zwei Seiten sind zueinander parallel.
m Mittelparallele (Mittellinie)
Parallelogramm
(Rhomboid)
Alle Höhen, Seitenhalbierenden und Winkelhalbierenden
schneiden einander im gleichen Punkt und sind gleich lang.
Vierecke u Umfang; A Flächeninhalt; e, f Diagonalen
Rechteck
Die Diagonalen halbieren einander.
Gegenüberliegende Winkel sind gleich groß. Gegenüberliegende
Seiten sind zueinander parallel und gleich lang.
Drachen
Die Diagonalen sind gleich lang und halbieren einander.
Alle Innenwinkel sind gleich groß (90°). Gegenüberliegende
Seiten sind zueinander parallel und gleich lang.
Quadrat
Die Diagonalen sind zueinander senkrecht, gleich lang und
halbieren einander.
Alle Innenwinkel sind gleich groß (90°). Alle Seiten sind gleich
lang.
Die Diagonalen sind zueinander senkrecht.
Mindestens zwei gegenüberliegende Winkel sind gleich groß.
Strahlensätze
Wird ein Strahlenbüschel
von Parallelen (zueinander
parallelen Geraden) und geschnitten, so entstehen
Strahlenabschnitte und Parallelenabschnitte.
Rhombus
(Raute)
Die Diagonalen sind zueinander senkrecht und halbieren
einander.
Alle Seiten sind gleich lang. Gegenüberliegende Seiten sind
zueinander parallel.
1.
Abschnitte auf einem Strahl verhalten sich zueinander wie
die gleichliegenden Abschnitte auf einem anderen Strahl:
2.
Gleichliegende Parallelenabschnitte verhalten sich
zueinander wie die zugehörigen Abschnitte auf einem
gemeinsamen Strahl:
3.
Abschnitte auf einer Parallelen verhalten sich zueinander wie
die zugehörigen Abschnitte auf der anderen Parallelen: