Formelsammlung als PDF herunterladen

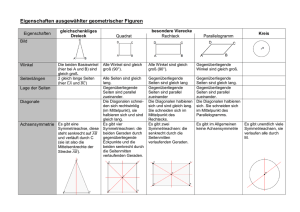
maths2mind®
Seite 90 von 183
Geometrie ebener Figuren und Körper
Kapitel: Vierecke
U  a  a  a  a  4a;



A  a  a  a2 ;
d  e  f  a  2;
267
Quadrat
a
ri  ;
2

d a

2
2
U  4  a;
ru 
A  a  ha  b  hb ;
268
Raute bzw. Rhombus
A


ef
 a2  sin  ;
2
e 2  f 2  4a2 ;

h h
ri  a  b ;
2 2


U  2(a  b);
269
271
Deltoid bzw.
Drachenviereck
Parallelogramm bzw.
Rhomboid
A
ef
;
2

U  a  b  a  b  2(a  b);

A  a  ha  b  hb  a  b  sin  ;

e 2  f 2  2(a2  b2 );

ha  b  sin  ;

U  a  b  a  b;
272
Trapez
A
ac
 h;
2


478
Diagonale
Alle 4 Seiten a sind gleich lang: gleichseitig
Alle 4 Innenwinkel sind rechte Winkel: rechtwinkelig
Die beiden Diagonalen sind gleich lang,
rechtwinkelig zu einander und halbieren einander
Der Schnittpunkt der beiden Diagonalen M, ist
sowohl der Inkreis- als auch
derUmkreismittelpunkt
Alle 4 Seiten sind gleich lang.
Die einander gegenüber liegenden Seiten sind
parallel, die einander gegenüber liegenden Winkel
sind gleich groß.
Der Schnittpunkt der beiden Diagonalen M, ist der
Inkreismittelpunkt
Es gibt 2 Paare gleich langer benachbarter Seiten.
Die Diagonalen stehen im rechten Winkel
zueinander und die Diagonale „e“ halbiert die
Diagonale „f“.
Die einander gegenüber liegenden Seiten sind
parallel, die einander gegenüber liegenden Winkel
sind gleich groß
Gegenüberliegende Seiten sind gleich lang und
parallel.
Gegenüberliegende Winkel sind gleich groß, je 2
benachbarte Winkel ergeben zusammen 180°.
Die beiden Diagonalen halbieren einander im
Schnittpunkt M.
2 Seiten (die Grundseiten) sind zueinander parallel
(a, c), die längere Seite (a) bezeichnet man als Basis,
die beiden nicht parallelen Seiten (b, d) nennt man
Schenkel.
Die Höhe h ist der Abstand der beiden parallelen
Seiten.
Die beiden Diagonalen (e, f) schneiden einander im
gleichen Verhältnis.
Als Diagonale bezeichnet man die
kürzest mögliche Verbindung zweier
einander gegenüber liegender
Eckpunkte in Vielecken.
Stand vom: 10.04.2016
Die jeweils aktuellste Version findet sich auf: maths2mind.com
Für dieses Werk nehmen wir u.a. §40f und §6 UrhG in Anspruch.
Es darf unentgeltlich weitergegeben, jedoch nicht verändert werden.