Das 3 x 3 Geobrett

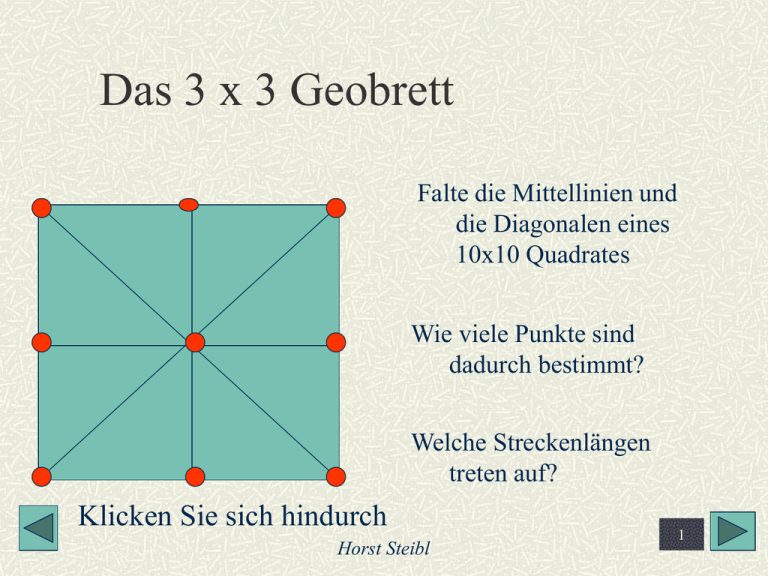
Das 3 x 3 Geobrett
Falte die Mittellinien und
die Diagonalen eines
10x10 Quadrates
Wie viele Punkte sind
dadurch bestimmt?
Welche Streckenlängen
treten auf?
Klicken Sie sich hindurch
Horst Steibl
1
Längen auf dem Geobrett
Wie lang sind die Dreiecksseiten eines 10 x 10 Quadrates?
10;10;14
10;11;11
7;11;11
7;10;11
7;7;10
5;11;14
5;5;7
5;7;11
Horst Steibl
2
Die 11-er-Linie
die goldene Linie im Quadrat
½
x² = 1² + ( ½ )²
x
1
x = 5/4 = ½ * 5
x= 1,118...
½
Und damit haben wir die Konstante des goldenen
Schnittes t = ½ + ½ *  5 =1,618...
Die 11-er-Linie im 10 x 10 Quadrat ist also 11,18.. cm lang
Horst Steibl
3
Flächeninhalt der Dreiecke
½
4/8
1/8
¼
¼ - 1/8
Horst Steibl
½
-¼
3/8
4
Gleich oder verschieden?
Die vier möglichen Drehlagen
Wie viele Lagemöglichkeiten hat das (10,11,14) - Dreieck?
Horst Steibl
5
Spiegelbilder
1
4
3
2
Wo liegen die Drehlagen des ersten Dreiecks?
Gib die Anzahl der möglichen Lagen für jedes Dreieck an
Horst Steibl
6
Winkel
Gleich oder verschieden
spitzer als....
Wo liegt der spitzeste Winkel?
ein Rechter
Horst Steibl
stumpfer als...
7
Die 10 Klassen gleich großer Winkel
Zeichne (falte) die 8 Dreiecke auf 4 Blättchen.
Suche den spitzesten Winkel und kennzeichne ihn mit 1.
Beachte dabei "Im Dreieck gilt: der kürzesten Seite liegt
der spitzeste Winkel gegenüber". Suche alle Winkel der 8
Dreiecke, die genauso groß sind, und kennzeichne sie
ebenfalls mit der 1.
Horst Steibl
8
10
........
2
7
5
1
8
6
3
4
9
Suche den nächst größeren Winkel, kennzeichne ihn in den
entsprechenden Dreiecken mit 2.
Fahre entsprechend fort. Du musst 10 verschiedene Winkel
finden.
Färbe die spitzen Winkel rot, die stumpfen Winkel grün, die rechten
(R) blau.
Vervollständige: Es gibt 10 Klassen verschieden großer Winkel.
Davon sind ... kleiner als 45, ... größer als 45 und kleiner als 90 ,
... sind größer als 90.
Miß die 10 Winkelgrößen.
9
Horst Steibl
Ordnung der Winkelgrößen
Beginne mit dem kleinsten
<1 + <2 = 45°
<3 = 2*<1
9
1
10
<4 = 2*<2
<5 = 45°
2
8
5
<6 = <1 + 45°
<7 = <2 + 45°
3
4
<8 = 90°
<9 = 90° +<2
<10= 90° + 45°
6
Horst Steibl
7
10
Die exaktenWinkelwerte
Im dunkelblauen Dreieck
(in der Reihenfolge der Berechnung)
9
<2 ; tan a = ½ ; a = 26,52°
10
1 2
<1 + <2 = 45°= <3
<1 = 45°- 26,52° = 18,44°
8
3
<4 = 2 * <1= 36,88°
5
<5=2* <2 = 63,4°
4
<6= 45° + <1= 63,44°
<7 = 45° + <2= 71,66°
<8 = 90°
7
6
<9 = 90° + <2= 116,52°
Horst Steibl
<10 = 90° + 45°=135
11
Vierecke und ihre Diagonalen
Welche Diagonaleigenschaften findest du jeweils?
Was ist hier?
Senkrecht, halbiert, gleich lang, ...
Und hier?
Horst Steibl
12
Haus der Vierecke
definiert über die Diagonaleigenschaften
e halbiert f
e,f teilen im gl. Verh.
e,f gl. Verhältnis
e,f gl. Verhältnis
e,f gl. Verhältnis
e,fVerhältnis
gl. Verhältnis
e,f gl.
e halbiert f
e halbiert
f
e halbiert
f
e,f gl. Verhältnis
e halbiert
e halbiert
f f
e halbiert f
e,f gl. Verhältnis
e,fe,f
gl. gl.
Verhältnis
e halbiert f
Verhältnis
e
halbiert
f
e
halbiert
f
e halbiert f
gleich
lang
gleich
lang
e halbiert
f f
gleich
lang
e halbiert
senkrecht
senkrecht
f
halbiert
e
e e,f
gleich
lang
f
senkrecht
e
halbiert
f
halbiert
ff halbiert
e halbiert
f ee f
gl.
Verhältnis
gleich
lang
e,f
gl. Verhältnis
gleich
lang
e,f
gl.
Verhältnis
e
halbiert
e
halbiert
ff
e halbiert
f e halbiert
esenkrecht
halbiert
f
f halbiert
e
senkrecht
e
halbiert
f
f
halbiert
e
e,f teilene,fim
gl.
Verh.
e,f
gl.
Verhältnis
gleich lang
gl. Verhältnis
halbiert
f ehalbiert
e
ee lotrecht
f f f
f halbiert e e halbiert
halbiert
f
e,f
gl.
Verhältnis
gleich lang
senkrecht
fehalbiert
e gleich lang
f
;
e halbiert
f ef
halbiert
e,f
gl.
Verhältnis
gleich
lang
gleich lang
esenkrecht
halbiert f
senkrecht
f
halbiert
e
f
halbiert
e
e halbierte,ffe,f
gl. gl.
Verhältnis
Verhältnis
e halbiert
f f
e halbiert
f halbiert gleich
e lang
senkrecht
gleich lang
senkrecht
e lotrecht f
gleich
lang
senkrecht
e halbiert
f
e
halbiert
f
gleich
lang
senkrecht
e halbiert
e halbiert f e halbiert f
gleich
lang f
senkrecht
f halbiert
e
f halbiert
ehalbiert
halbiert
halbiert
e halbiert
gleich lang
senkrecht
fehalbiert
fehalbiert
eehalbiert
f f ef
e halbiert
f ef f
ef
fgleich
halbiert
fsenkrecht
halbiert
e halbiert f
e halbiert
ffgleich
halbiert
elang
f halbiert
e e ef halbiert
halbiert
ee
f halbiert
lang
egleich
lotrecht
f senkrecht
f halbiert
e
f halbiert e
egleich
halbiert
esenkrecht
halbiert f
senkrecht
lang
senkrecht
langf
lang
senkrecht
fehalbiert
fehalbiert
gleich
lang
senkrecht
halbiert
f eff ; gleich
e halbiert
f ef
halbiert
halbiert
e ehalbiert
senkrecht
e halbiert
flanglang
13
senkrecht
egleich
halbiert
f
gleich
halbiert
e e
f halbiert
e e
f halbiert
f
halbiert
gleich
lang
f f halbiert
e f halbiert
Horst
Steibl
ehalbiert
gleich lang
fe
halbiert
e halbiert
f ef
senkrecht
e halbiert f
se
eh
5 Größen notwendig
Hasse-Diagramm: ...ist Teilmenge von...
4 Größen
1 def. Eigensch.
e,f gl. Verhältnis
e halbiert f
2 def. Eig.
3 Größen
gleich lang
e,f gl. Verhältnis
e halbiert f
f halbiert e
senkrecht
e halbiert f
3 def. Eigensch
2 Größen notw.
gleich lang
e halbiert f
f halbiert e
senkrecht
e halbiert f
f halbiert e
4 definierende Eigernschaften
senkrecht
gleich lang
Horst
Steibl
e halbiert
f
1 Konstruktionsgöße
14
Ein Gleich-Recht-Diagoneck
Begründe den Namen!
2 Elfer-Strecken lotrecht
als Diagonalen:
Hypothese:
Das Mittenviereck eines
Gleich-Recht-Diagonecks
ist ein Quadrat.
Allgemein gilt:
Das Mittenviereck eine
beliebigen Vierecks ist ein.....
Ein Viereck heiße RechtEin Viereck heiße Gleichwenn....
Diagoneck, wenn...
HorstDiagoneck,
Steibl
15
Das Mittenviereck eines Vierecks ist immer
ein Parallelogramm
D
Vergleiche die Diagonalen
mit den Parallelogramseiten
C
Warum sind die roten Parallelogramseiten parallel zur roten Diagonale
und genau halb so lang?
A
Deute das Dreieck ACD als
Strahlensatzfigur
Horst Steibl
16
Der Drittel-Punkt
5cm
3,7cm
9,4cm
Zeichne die Figur mit den Diagonalen
4,7cm im 10-er-Blättchen und miss die
Diagonalabschnitte. Was fällt auf?
7,4cm
Wie heißt die rote Figur? Welcher
Satz kommt zur Anwendung?
10cm
Allgemein gilt: Im Trapez teilen die Diagonalen einander
im Verhältnis der parallelen Seiten.
Hier teilen sie sich also im Verhältnis 2 : 1
Zeichne den Drittel-Punkt und falte zum 9-er-Feld
Horst Steibl
17
Der Fünftel-Punkt
Begründe die Ähnlichkeit
1
2
3
4
der bunten Dreiecke.
Die Katheten stehen also im
Verhältnis 1 : 2
Damit teilt der Fünftel-Punkt die
11-er-Strecken einmal 1 : 4 und
zum anderen 2 : 3
Zeichne einen solchen Fünftel-Punkt und falte
zum 25-er-Feld
Horst Steibl
18
Die goldigen Vierecke
die durch vier 11-er-Linien bestimmten Vierecke
Bringe auf dem Geo-Brett zwei 11-er-Parallelogramme zum Schnitt. Es gibt drei verschiedene
Vierecke?
Den Flächeninhalt der Raute über der
Mittellinie kannst du leicht bestimmen!
Warum ist das Quadrat ein Quadrat? Schätze
den Flächeninhalt (als Bruchteil von 1).
Zeichne die Figuren, zerschneide geeignet und
lege so, dass die Bruchteile deutlich werden.
Bei dem Quadrat und der Raute über der
Diagonalen musst du die Dreiecke umlegen.
Horst Steibl
19
Die Drachen über der Diagonale und über der Mittellinie
Diese Bruchteile sind nicht ganz so einfach
Die Fläche dieses Dreiecks kennst du aus
der Quadrataufgabe. Sie ist ¼ des kleinen
Quadrates also 1/..
Wenn du von dem 5,10,11-Dreieck
das blaue abziehst, bleiben für das
rote Viereck also...
Um dieses ockerfarbige Dreieck zu
bestimmen, muss man den Drittel-Punkt
kennen Dieser drittelt jede Querlinie,also
auch die Linie, auf der die Höhe liegt.
½ * 1/3 * 1/2 = 1/ 12
Warum sind die noch abzuschneidenden
Dreiecke jeweils 1/5?
20
Horst Steibl
Trapeze
Bestimme den Flächeninhalt als Bruchteil von 1
Bedenke: der Drittel-Punkt
drittelt,
der Fünftel-Punkt fünftelt jede
Querstrecke in Streifen, damit
kennst du die Dreieckshöhe
Bestimme für die parallelen
Seiten den Bruchteil der
Elferlinien und berechne A
Es gibt noch zwei kleine Vierecke,
nach der Formel a = m * h
die sind zwei großen ähnlich.
Welche sind das?
Horst Steibl
21
Die goldigen Vierecke auf dem Geobrett
Ordne die Namen den
Figuren zu:
Quadrat
Raute über der Diagonalen
Raute über der Mittellinie
Drachen über der Diagonalen
Drachen über der Mittellinie
Rechtwinkliges Trapez
Trapez
Horst Steibl
22
Bruchteile
4 *(1/4 * 1/5)
1/
6
*½
1/
3
?
1/
20
?
+ 3 /20
Und wo ist dies Viereck?1 – 1/4 – 1/5 - 1/12 =4/15
Horst Steibl
23
Die Mittelsenkrechten von vier 11-er-Linien
erzeugen ein Quadrat
Falte die Kantenmitten.
Bringe die Ecke r. u. auf die obere
Mitte.
Drehe das Blatt um 90°.
Bringe die Ecke r. u. auf die obere
Mitte (insgesamt also viermal).
Färbe das mittlere Quadrat rot.
Falte die 4 dazu parallelen 11-erLinien.
Färbe ein Eckquadrat blau.
Horst Steibl
24
Berechnung des mittleren Quadrates
Klicke dir zunächst den ganzen Text her
Die 11-er-Linie halbiert die
Hälfte der MS, also
¼g
Der Pfeil
ist aber 1/5g
Dreieck ist ähnlich, Katheten
also 1 : 2
¼g - 1/5g = 1/20g; somit zweite
Kathete 1/10g
Die obere Hälfte von g setzt
sich zusammen aus
1/5g + 1/10g + 1/5g
Damit berechnet sich das
mittlere Quadrat
(1/5 * ½ 5 * a)²= 1/20 a²
Horst Steibl
25
Die Mittelsenkrechten der 11-er-Linien
erzeugen ein Quadrat ¼ von 1/5
Quadrat der 11-er-Linien
1/5 des Quadrates
d(P20;P19)*d(P20;P19)
Aktueller Wert : 20
11,18
11,18 cm
cm
2,236
2,236 cm
cm
1,118
1,118 cm
cm
d(P10;P21)*d(P10;P21)
Aktueller Wert : 5
Quadrat aus den
Mittelsenkrechten
der 11-er-Linien
1/20 des großen
1/4 des kleinen
d(P21;P20) * d(P21;P20)
Aktueller Wert : 1,25
4,472 cm
Eckquadrat
1/80 des ganzen
1/4 des roten
Quadrates
Horst Steibl
26