Der Satz von Haga
Werbung
Slide 1
Der Satz von Haga
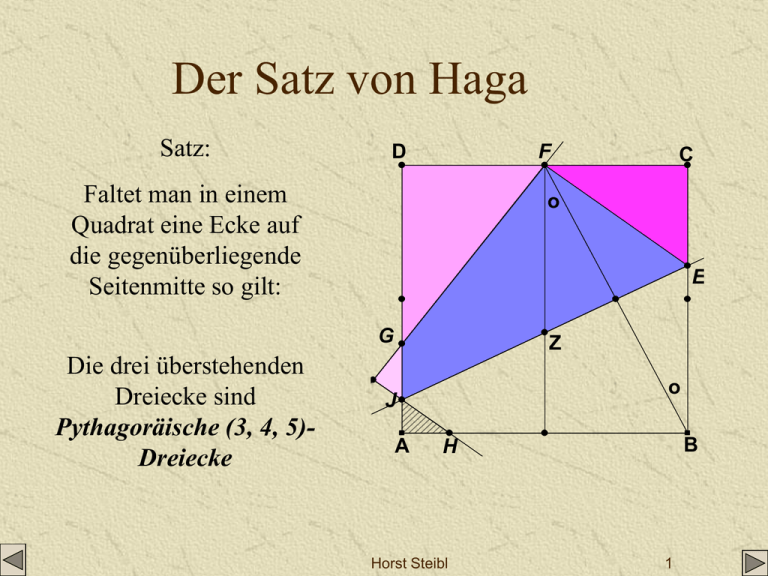
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 2
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 3
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 4
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 5
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 6
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 7
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 8
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 9
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 10
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 2
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 3
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 4
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 5
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 6
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 7
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 8
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 9
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10
Slide 10
Der Satz von Haga
Satz:
D
F
Faltet man in einem
Quadrat eine Ecke auf
die gegenüberliegende
Seitenmitte so gilt:
o
E
G
Die drei überstehenden
Dreiecke sind
Pythagoräische (3, 4, 5)Dreiecke
C
Z
o
J
A
B
H
Horst Steibl
1
y
5,5
Das (3,4,5)-Dreieck auf 5dem Geobrett
4,5
3
1
4
2
Das (5, 10, 11)Dreieck wird durch die
4 11-er-Linie) in zwei zum
Höhe (zweite
Ausgangdreieck ähnliche Dreiecke geteilt.
3,5
Die Katheten stehen in allen drei (blau,
lila, lila-blau)
3 Dreiecken im Verhältnis
1 : 2. Damit ergibt sich für das lila und das
2,5 1 : 2 = 2 : 4. Die eine 11blaue Dreieck
Linie wird 2also im Verhältnis 1: 4, die
andere im Verhältnis 2 : 3 geteilt. Die
Hypotenuse1,5
des grünen Dreiecks ist damit
5 solcher Einheiten lang
1
Damit ist gezeigt, dass das
grüne Dreieck ein
-5ägyptisches
-4,5 -4 -3,5
-3 -2,5 -2 -1,5
(3,4,5)-Dreieck
ist
0,5
-1
-0,5
Horst Steibl
0,5
-0,5
1
1,5
2
2,5
2
3
3,5
y
5,5
Die Winkel im ägyptischen Dreieck
5
oo
o i
i
o
4,5
Den spitzesten
Winkel im
(5,10,11)-Dreieck
nennen
4
wir Tom (o) , den spitzen
Winkel3,5
im(5,11,14)-Dreieck
nennen3 wir Tim (i).
î + o = 2,5
45°
R=o+i+i+o
Damit gilt:2 Genau dann ist ein
rechtwinkliges Dreieck ein ägyptisches
1,5 ein spitzer Winkel ein
Dreieck, wenn
oo-Winkel1 oder ein ii-Winkel ist
Ein gestreckter Winkel kann zerlegt werden in oiiooiio
bzw. iooiiooi. Gestreckter
0,5
Winkel heißt also 4 o + 4 i. Ein rechter Winkel hat immer 2 o und 2 i Winkel.
Dreieck
immer-14 o-0,5
und 4 i. 0,5 1 1,5 2 2,5 3 3,5
-5 Die
-4,5Winkelsumme
-4 -3,5 -3 im
-2,5
-2 -1,5
-0,5
Horst Steibl
3
4
Trigonometrische Einsichten
26,6 °
53,1 °
Im blauen Dreieck gilt:
o = arc tan( ½ ) = 26,6..
Im lila Dreieck gilt:
oo = arc tan ( 4/3 ) = 53,1..
Damit ist auch gezeigt:
2 * arc tan ( ½ ) = arc tan ( 4/3 )
Horst Steibl
4
Der Satz von Haga
D
F
C
oo
ii
ii o o
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
Z
o
B
Falte die Mittelparallele des
Quadrates (C auf D). Öffne und
falte B aufo F. Öffne und falte E auf
o
Z. Du hast im rechten
Doppelquadrat (bzw Halbquadtrat)
die Diagonale und deren
Mittelsenkrechte gefaltet. Öffne
und falte wieder B auf F. Knicke
die überstehenden Dreiecke um und
wieder zurück.
Begründe die Winkelangaben in der
Reihenfolge ihres Erscheinens
Horst Steibl
5
Begründung
Der spitzeste Winkel im (5,10,11)-Dreieck laut Definition o
Durch Faltung o = o
D
F
C
oo
ii
ii o o
ii rechter Winkel
Doppelquadrat
o rechten
o
oo 2. Winkel im rechtwinkligen Dreieck
oo
iio
E
oii
ii
G ooiioo
ii oii
oo iio
J
oo
A
H
ii rechter Winkel im blauen Viereck
oo rechter Winkel im linken Doppelquadrat
ii 2. Winkel im rechtwinkligen Dreieck
ii Scheitelwinkel
Z
oo 2. Winkel im rechtwinkligen Dreieck
o
ooiioo gestreckter Winkel
B
iio oii Winkelsumme im stumpfwinkligen Dreieck
oii Winkelsumme im blauen Viereck
Alles klar?
oo Scheitelwinkel
iio gestreckter Winkel
Horst Steibl
6
Längen der Abschnitte auf den Quadratseiten
D
F
C
E
G
Wir gehen von einem Quadrat mit der
Seitenlänge 1 aus. Wie lang sind die Seiten
der ägyptischen Dreiecke? Oder: Wie teilen
o
E, G und J dieo Quadratseiten?
CE = ?
DG = ?
Z
GJ =?
J
A
H
¼ * ½ *3 = 3/8
1/
2/
*
½
*
4
=
3
3
1/
8
* 1/3 * 5 = 5 / 24
1/
8
* 1/3 * 3 = 3 / 24 = 1/8
B
JA = ?
Begründe die Rechnung!!!
Horst Steibl
7
Begründung der Berechnung
D
F
C
E
G
DG = ?
1/
J
H
FC sind 4 Einheiten. Eine Einheit ist
also ¼ * ½ . Davon muss ich 3
o
Einheiten
für o
CE haben
¼ * ½ *3 = 3/8
DF entspricht 3 Einheiten. Eine Einheit ist also
1/ * ½ . Für DG brauche ich 4 davon .
3
Z
A
CE = ?
2/
*
½
*
4
=
3
3
B
Die Dreiecke GKJ und AHJ sind kongruent. Der Strecke GA entsprechen also
5 + 3 = 8 Einheiten. GA ist 1/3. GJ somit 5/8 * 1/3 und JA somit 3/8 * 1/3 .
Horst Steibl
8
Noch ein ägyptisches Dreieck!!!
D
F
C
E
G
Z
J
A
H
B
Faltet man dieozwei überstehenden
großen ägyptischen Dreiecke nach
o einem
innen, so setzen sich diese zu
weiteren ägyptischen Dreieck
zusammen.
Der spitze Winkel bei E berechnet sich iio
– oo ~ 10,2... °, der stumpfe Winkel bei G
mit
ooiioo – ii = oooo = 106,5..°, der
Winkel bei J ist oii = 63,.. °. Damit ergibt
sich die Winkelsumme im blauen Dreieck
iiooooii
Berechne die Seitenlängen des Dreiecks GEF
Horst Steibl
9
Berechnung der Seitenlängen des Dreiecks GEF
D
F
C
EF sind 5 Einheiten von den 4
Einheiten von FC
6,25 cm
o o
5 cm
8,33 cm
E
L
3,75 cm
25/24
1,042
L
G
EF = EB = 5 * 1/4 * ½ = 5/8
Z 10,42 cm
FL == ½
6,67 cm
J
A
H
B
GL = DG = 2/3
EL = EC =3/8
FG =5 * 1/3 * ½ = = 5/6
GE = 2/3 + 3/8 = 25/24
Horst Steibl
10