Optische Abbildungen
Werbung
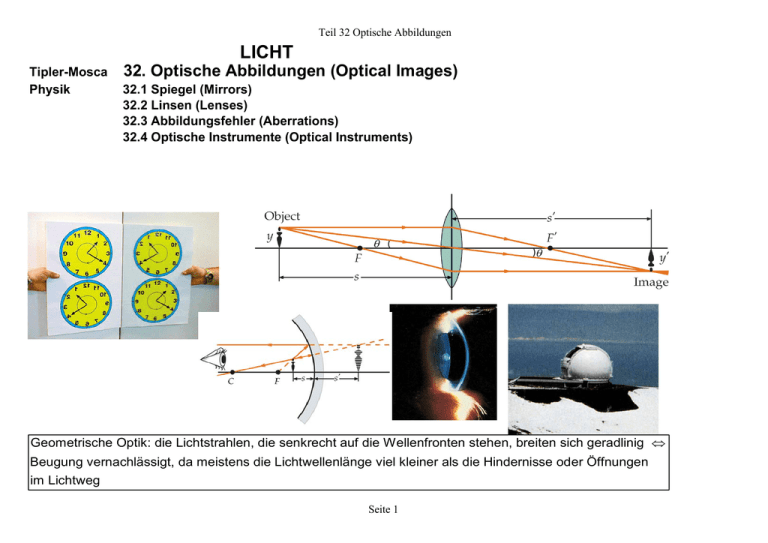
Teil 32 Optische Abbildungen LICHT Tipler-Mosca Physik 32. Optische Abbildungen (Optical Images) 32.1 Spiegel (Mirrors) 32.2 Linsen (Lenses) 32.3 Abbildungsfehler (Aberrations) 32.4 Optische Instrumente (Optical Instruments) Geometrische Optik: die Lichtstrahlen, die senkrecht auf die Wellenfronten stehen, breiten sich geradlinig ⇔ Beugung vernachlässigt, da meistens die Lichtwellenlänge viel kleiner als die Hindernisse od er Öffnungen im Lichtweg Seite 1 Teil 32 Optische Abbildungen Seite 2 Teil 32 Optische Abbildungen 32.1 Spiegel (Mirrors) Ebene Spiegel Bilderzeugung beim ebenen Spiegel: Lichtstrahlenbündel von einer Punktquelle P (Gegenstand) wird am ebenen Spiegel reflektiert ⇒ nach der Reflexion laufen die Strahlen so auseinander, als gingen sie vom Punkt P' (Bild des Gegenstands) hinter der Ebene des Spiegels aus (virtuelles Bild). virtuelles Bild Spiegelsymmetrie rechte Hand ⇒ Spiegelbild linke Hand Abbildung eines rechtwinkeligen kartesischen Koordinatensystems durch einen ebenen Spiegel ⇒ Richtung der z-Achse (ez ) durch Spiegelung umgekehrt ( − ez ) ⇒ aus rechtshändigem Koordinatensystem ex × ey = ez linkshändiges Koordinatensystem ex × ey = −ez Seite 3 ⇒ Teil 32 Optische Abbildungen virtuelles Bild Konstruktion des Spiegelbildes eines Pfeils beim ebenen Spiegel ⇒ das virtuelle Bild hinter der Spiegelebene hat von dieser den selben Abstand (Bildweite b ) wie der Gegenstand vor ihr (Gegenstandsweite g ), das Bild ist aufrecht und gleich groß wie der Gegenstand g b Mehrfachabbildungen entstehen, wenn zwei ebene Spiegel gegeneinander geneigt sind (Winkelspiegel). Wie viele Mehrfachbilder an zwei zueinander geneigten Spiegel entstehen, hängt ab vom Winkel zwischen beiden Spiegeln und von der Position des Gegenstands relativ zu ihnen. virtuelles Bild Ein waagrechter Strahl trifft auf zwei senkrecht stehenden Spiegel, die einen rechten Winkel einschließen ⇒ der austretende Strahl verläuft parallel zur Einfallsrichtung, unabhängig von Einfallswinkel am ersten Spiegel. Drei Spiegel senkrecht zueinander angeordent ⇔ Retroreflektor oder Katzenauge Seite 4 Teil 32 Optische Abbildungen Sphärischer Spiegel Konkavspiegel Zur Berechnung der Bildweite b aus der Gegenstandsweite g und dem Krümmungsradius r Dreieck PCA: aus α + θ + 180° − β = 180° ⇒ β = α + θ , achsennahe Strahlen Dreieck PP'A: aus α + 2θ + 180° − γ = 180° ⇒ γ = α + 2θ optische Achse ⇒ Elimination von θ ⇒ 2β = α + γ ⇒ achsennahe Strahlen ⇒ ⇒ α≈ reelles Bild g, β ≈ r, γ ≈ b ⇒ 1 1 2 + = g b r g b optische Achse Krümmungsmittelpunkt Sphärische Abberation: Strahlen, die nicht achsennah sind, werden nicht im Bildpunkt P' reflektiert ⇒ Bild unscharf Alle achsennahen Strahlen, die vom Gegenstandspunkt P ausgehen, gelangen nach der Reflexion am Hohlspiegel zum Bildpunkt P' Seite 5 reelles Bild Teil 32 Optische Abbildungen Zur Berechnung des Abstands y ' des Bildpunkts von der optischen Achse g b Scheitelpunkt des Spiegels Parallele Strahlen (ebene Wellenfronten) werden in einem Punkt auf der Brennebene reflektiert, wobei die Wellenfronten kugelförmig werden. Brennebene für PSP' ⇒ zwei rechtwinkelige Dreiecke ⇒ y' b ähnliche Dreiecke ⇒ =− y g aus 1 1 2 + = für g g b r r ⇒ 1 2 r = ⇒ b = = f Brennweite b r 2 1 1 1 + = g b f Seite 6 Brennweite Teil 32 Optische Abbildungen Reflexion ebener Wellen an einem Konvexspiegel. Die abgehenden Wellenfronten sind kugelförmig und scheinen vom Brennpunkt F hinter dem Spiegel auszugehen Umkehrbarkeit des Lichtweges Beispiel 32.1: Abbildung durch einen Konkavspiegel Punktförmiger Gegenstand bei g = 12 cm und y = 3 cm vor einem Konkavspiegel mit r = 6 cm. Gesucht: a) Brennweite f , b) Bildweite b, c) Abstand y ' des Bildpunkts von der optischen Achse ⇒ Teil a) f = r 2 = ( 6 cm ) 2 = 3 cm, 1 1 1 1 1 1 1 1 1 + = ⇒ + = ⇒ = − g b f 12 cm b 3 cm b 3 cm 12 cm y' b b 4 cm Teil c) aus Gl. (32.2) =− ⇒ y ' = − y = − ( 3 cm ) = −1 cm y g g 12 cm Teil b) aus Gl. (32.4) Seite 7 ⇒ b = 4 cm, Teil 32 Optische Abbildungen Bildkonstruktion bei sphärischen Spiegeln achsenparalleler Strahl Brennpunktstrahl Konstruktion des Bilds am Hohlspiegel mit Hilfe von drei Hauptstrahlen: der achsenparallele Strahl, der Brennpunktstrahl, der Mittelpunktstrahl Mittelpunktstrahl Näherungsweise Konstruktion des Bild eines Hohlspiegels Seite 8 Teil 32 Optische Abbildungen g b Konkavspiegel mit Gegenstand zwischen Brennpunkt und Spiegel ⇔ g < f ⇒ Bild ist virtuell und aufrecht, und scheint hinter dem Spiegel auszugehen ⇔ b < 0. Vorzeichenkonvention für Konkav- oder Konvexspiegel zur Verwendung von 1 1 1 + = g b f g b Ein reelles Bild kann nur vor dem Spiegel entstehen, also auf der selben Seite wie das reflektierte Licht (und der Gegenstand). Virtuelle Bilder entstehen nur hinter dem Spiegel, wo sich kein Strahl vom Gegenstand ausbreiten kann. Seite 9 Teil 32 Optische Abbildungen Das Verhältnis der Bildhöhe P'Q' = y ' zur Gegenstandshöhe PQ = y nennt man Vergrößerung oder Abbildungsmaßstab (Lateralvergrößerung) =− beim ebenen Spiegel: r = ∞ ⇒ b = −g Vergrößerung m = − b g = +1 ⇒ b g Konvexspiegel Bildkonstruktion beim Konvexspiegel ⇒ das Bild ist virtuell, aufrecht und verkleinert g b Konvexspiegel zur Überwachung Seite 10 Teil 32 Optische Abbildungen Beispiel 32.2 Abbildung durch einen Konvexspiegel Gegenstand mit y = 2 cm steht mit g = 10 cm vor einem Konvexspiegel mit r = −10 cm. Gesucht: a) Bildweite b, b) Bildhöhe y ' ⇒ g 1 1 1 r Teil a) mit Gl. (32.4) + = und Gl. (32.3) f = ⇒ g b f 2 1 1 1 3 −10 cm 1 + = ⇒ =− ⇒ b = −3.33 cm, f = = −5 cm ⇒ 10 cm b 2 10 cm b −5 cm y' b −3.33 cm Teil b) aus Gl. (32.5) m = =− =− = +0.333 ⇒ y g 10 cm y ' = my = +0.333 ( 2 cm ) = 0.666 cm zur Übung Beispiel 32.3: Ermitteln die Bildweite mögliches Prüfungsbeispiel Seite 11 b Teil 32 Optische Abbildungen 32.2 Linsen (Lenses) Entstehung des Bildpunktes P' durch Brechung der Lichtstrahlen aus dem Gegenstandspunkt P an einer spährischen Oberfläche Durch Brechung erzeugte Bilder aus dem Snellius'schem Brechungsgesetz n1 sinθ1 = n2 sin θ 2 ⇒ für kleine Winkel n1θ1 = n2θ 2 ⇒ g b für Dreieck ACP' θ 2 + γ + 180° − β = 180° ⇒ β = θ 2 + γ = = ( n1 n2 ) θ1 + γ ⇒ für Dreieck ACP α + β + 180° − θ1 = 180° ⇒ θ1 = α + β ⇒ Elimination von θ1 β = ( n1 n2 )(α + β ) + γ ⇒ ⇒ n1α + n2γ = ( n2 − n1 ) β ⇒ ⇒ n1α + n1β = n2 β + n2γ für kleine Winkel α ≈ g , β ≈ r ,γ ≈ b n2 > n1 ⇒ n1 n2 n2 − n1 + = g b r g b Bei der Brechung entstehen reelle Bilder, vom Gegenstand aus gesehen, hinter der Brechfläche (Transmissionsseite). Virtuelle Bilder entstehen vor der brechenden Fläche (Einfallsseite). Seite 12 Teil 32 Optische Abbildungen Vorzeichenkonvention für die Brechung g b Beispiel 32.4: Vergrößerung durch eine brechende Oberfläche y −y ' und tan θ 2 = ⇒ g b y −y ' für kleine Winkel θ1 = und θ 2 = , g b aus dem Snellius'schen Brechungsgesetz ⇒ n1 sinθ1 = n2 sinθ 2 aus der Bildkonstruktion tan θ1 = b für kleine Winkel n1θ1 = n2θ2 g ⇒ θ1 und θ2 eingesetzt ⇒ n1 Vergrößerung m = =− n1b n2 g Seite 13 nb y' =− 1 y n2 g −y ' y = n2 g b ⇒ ⇒ Teil 32 Optische Abbildungen Beispiel 32.5: Kater und Goldfisch mögliches Prüfungsbeispiel Beispiel 32.6: Scheinbare Tiefe im Wasser mögliches Prüfungsbeispiel Seite 14 Teil 32 Optische Abbildungen Dünne Linsen Betrachtung einer dünnen Linse mit Brechzahl n, umgeben von Luft mit Brechzahl 1. Die Krümmungsradien beider Linsenoberflächen sind r1 und r2 . An beiden Seiten einer Linse tritt Brechung auf. Gegenstand mit Abstand g von der ersten Oberfläche (bzw. von der dünnen Linse) ⇒ Bildweite b1 durch 1 n n −1 + = Brechung an der ersten Oberfläche aus Gl. (32.6) g b1 r1 g b1 b g2 ⇒ an der ersten Oberflächen gebrochenes Licht wird erneut gebrochen ⇒ die Strahlen treffen so auf die n 1 1− n n 1 1− n zweite Oberfläche, als gingen sie von P1' aus ⇒ g 2 = −b1 ⇒ bzw. + = + = ⇒ g2 b r2 r2 −b1 b Addition der beiden Gleichungen ⎛1 1⎞ 1 = ( n − 1) ⎜ − ⎟ f ⎝ r1 r2 ⎠ ⇒ ⎛1 1⎞ 1 1 n − 1 1− n + = + = ( n − 1) ⎜ − ⎟ ⇒ für g = ∞ und b = f ⇒ g b r1 r2 ⎝ r1 r2 ⎠ 1 1 1 + = g b f Zur Beachtung: Vorzeichenkonvention für Brechung unterscheidet sich von der Konvention für Reflexion ⇒ bei Linsen ist b positiv für Bilder auf der Transmissionsseite; für die Brennweite gemäß Gl. (32.11) gilt die Vorzeichenkonvention für eine einzelne brechende Oberfläche ⇔ r ist positiv, wenn der Krümmungsmittelpunkt auf der gleichen Seite der Oberfläche liegt wie das gebrochene Licht ⇒ für eine Bikonvexlinse ist r1 positiv und r2 negativ, so daß f positiv ist Seite 15 Teil 32 Optische Abbildungen Brennpunkt Wellenfronten einer ebenen Welle beim Durchlaufen einer Bikonvexlinse Brennpunkt (Sammellinse, falls Brechzahl des Linsematerials > Brechzahl des umgebenden Mediums) Strahlen einer ebenen Welle beim Durchlaufen einer Sammellinse Wellenfronten einer ebenen Welle beim Durchlaufen einer Bikonkavlinse (Zerstreuunslinse, falls Brechzahl des Linsematerials > Brechzahl des umgebenden Mediums ⇒ f negativ) Brennpunkt Lichtstrahlen, die vom Brennpunkt einer Sammellinse ausgehen, treten Strahlen einer ebenen Welle beim Brennpunkt Durchlaufen einer Sammellinse achsenparallel aus Wenn parallele Strahlen unter einem kleinen Winkel zur Achse der Sammellinse einfallen ⇒ Fokussierung in der Brennebene Seite 16 Teil 32 Optische Abbildungen 1 Der Kehrwert der Brennweite einer Linse nennt man Brechkraft D = , f -1 Einheit Dioptrie (dpt) = m , Die Brechkraft einer Linse ist ein Maß für ihre Fähigkeit, paralleles Licht zu bündeln. Beispiel 32.7: Die Brennweite einer Linse Bikonvexe dünne Linse aus Glas mit n = 1.5, r1 = 10 cm und r2 = −15 cm; gesucht: Brennweite f ⇒ aus Gl. (32.11) ⎛1 1⎞ 1 1 ⎛ 1 ⎞ ⎛ 1 ⎞ = ( n − 1) ⎜ − ⎟ = (1.5 − 1) ⎜ − = 0.5 ⎟ ⎜ 6 cm ⎟ f ⎝ 10 cm −15 cm ⎠ ⎝ ⎠ ⎝ r1 r2 ⎠ ⇒ f = 12 cm Beispiel 32.8: Die Brechkraft einer Linse Linse mit r1 = 10 cm und r2 = 13 cm und mit n = 1.5; gesucht: a) Brennweite f , b) Brechkraft D ⇒ Teil a) aus Gl. (32.11) ⎛1 1⎞ 1 1 ⎞ ⎛ 1 = ( n − 1) ⎜ − ⎟ = (1.5 − 1) ⎜ − ⎟= f r r 10 cm 13 cm ⎝ ⎠ 2 ⎠ ⎝ 1 3 ⎛ ⎞ = 0.5 ⎜ = 0.01154 cm-1 = 1.154 m-1 = 1.15 dpt ⇒ f = 86.7 cm ⎟ ⎝ 130 cm ⎠ 1 Teil b) D = = 1.15 dpt f Seite 17 Teil 32 Optische Abbildungen Die Bildkonstruktion bei Linsen achsenparalleler Strahl Bildkonstruktion mit Hilfe der Hauptstrahlen Mittelpunktstrahl Brennpunktstrahl Bei der Sammellinse ist das Bild reell und umgekehrt. y' b Vergrößerung der Sammellinse aus tanθ = =− y g Fresnel'sche Linse ⇒ Materialersparnis Seite 18 Teil 32 Optische Abbildungen Beispiel 32.9: Durch eine Linse erzeugtes Bild Gegenstand mit y = 1.2 cm steht g = 4 cm vor einer bikonvexen Linse mit f = 12 cm. Gesucht: Bildweite, Bildhöhe, Bild virtuell oder reell? Einzeichnen des achsenparallelen Strahls rechnerisch: 1 1 1 + = ⇒ g b f 1 1 1 1 1 1 = − = − =− b f g 12 cm 4 cm 6 cm ⇒ b = −6 cm; aus Gl. (32.12) Einzeichnen des Mittelpunktstrahls ⇒ Bild virtuell, aufrecht, vergrößert aus Gl. (32.14) m = −6 cm y b =− =− y' g 4 cm ⇒ m = +1.5 ⇒ y ' = my = ( +1.5 )(1.2 cm ) = 1.8 cm Einzeichnen des Brennpunktstrahls Seite 19 Teil 32 Optische Abbildungen Dicke Linsen Für die Bildkonstruktion bei dünnen Linsen können die Brechungen an den beiden Oberflächen der Linse durch eine einzelne Brechung an der Mittelebene der Linse ersetzt werden. Ist die Linse zu dick, dann muß man anstelle der Mittelebene mit zwei sogenannten Hauptebenen arbeiten, auf die sich Brennweite, Gegenstandsweite und Bildweite beziehen. Experimentelle Bestimmung der Hauptebenen: paralleles Licht lässt man nacheinander auf beide Seiten der Linse auftreffen, und der jeweilige Brennpunkt wird ermittelt ⇒ der Schnittpunkt der rückwärtigen Verlängerung des austretenden Strahles mit der Verlängerung des ankommenden parallelel Strahles liegt auf der betreffenden Hauptebene. siehe auch www.wikipedia.de Mehrere Linsen Mehrere Linsen befinden sich hintereinander auf der optischen Achse ⇒ Konstruktion des Endbildes: Ermittlung des von der ersten Linse entworfenen Bildes ⇒ dieses Bild ist Gegenstand für die Abbildung durch die zweite Linse ⇒ siehe Beispiel 32.10 und 32.11 Linsenkombinationen Zwei dünne Linsen mit Brennweiten f1 und f2 stehen auf derselben Achse dicht beieinander ⇒ Brennweite der Kombination: 1 1 1 = + f f1 f2 ⇒ Brechkraft: D = D1 + D2 , siehe Beispiel 32.12: Seite 20 Teil 32 Optische Abbildungen Beispiel 32.10: Durch eine zweite Linse erzeugtes Bild Gegenstand mit y = 1.2 cm steht g = 4 cm vor einer bikonvexen Linse mit f1 = 12 cm. Eine zweite Linse mit f2 = 6 cm wird 12 cm rechts von der ersten Linse plaziert. Gesucht: Bildweite b des Endbilds. Konstruktion für die erste Linse rechnerisch: aus Gl. (32.12) 1 1 1 + = ⇒ g1 b1 f1 1 1 1 1 1 1 = − = − =− b1 f1 g1 12 cm 4 cm 6 cm ⇒ b1 = −6 cm ⇒ Bild der Linse 1 ist Gegenstand für Linse 2 ⇒ g 2 = 18 cm ⇒ aus 1 1 1 + = ⇒ g 2 b2 f2 1 1 1 1 1 1 = − = − = b2 f2 g 2 6 cm 18 cm 9 cm Seite 21 ⇒ b2 = 9 cm Teil 32 Optische Abbildungen Beispiel 32.11: Kombination von Linsen mögliches Prüfungsbeispiel Beispiel 32.12: Zwei dicht beieinander stehende Linsen Zwei Linsen mit derselben Achse stehen dicht beieinander. Zu zeigen: aus Gl. (32.12) für die erste Linse 1 1 1 = + f f1 f2 ⇒ 1 1 1 + = , g b1 f1 für die zweite Linse mit g 2 = −b1 ⇒ 1 1 1 + = −b1 b f2 ⇒ Kombination der beiden Ausdrücke ⇒ 1 1 1 1 ++ = + g b f1 f2 Seite 22 Teil 32 Optische Abbildungen 32.3 Abbildungsfehler (Aberrations) Abbildungsfehler ⇔ wenn nicht alle von einem punktförmigen Gegenstand ausgehendne Strahlen in einem einzigen Bildpunkt fokussiert werden. Sphärische Aberration bei einer sphärischen Linse ⇔ achsenferne Strahlen werden nicht in einem Punkt fokussiert ⇒ der Einfluß der sphärischen Aberration kann verringert werden durch Ausblendung der achsenfernen Strahlen ⇒ Nachteil: das Bild ist weniger lichtstark die spharische Aberration kann vermieden werden durch geeignete Form der Linsen- bzw. Spiegelkrümmung ⇒ z.B. beim Spiegel ⇒ Parabolspiegel, bei Linsen ⇒ asphärische Linsen Astigmatismus schiefer Bündel: tritt auf wenn Strahlenbündel mit einem Winkel zur Achse einfallen ⇒ sie werden nicht in der Brennebene fokussiert ⇒ ein ausgedehnter Gegenstand wird zu den Bildrändern hin zunehmend unscharf abgebildet ⇒ Verzeichnung. Chromatische Aberration: tritt nur bei Linsen auf, nicht bei Spiegeln ⇔ rührt von der Disperion her ⎛1 1⎞ 1 = ( n − 1) ⎜ − ⎟ ⇒ für violettes Licht ist die Brennweite f etwas geringer als für rotes Licht. f ⎝ r1 r2 ⎠ Verringerrung der chromatischen Aberration erreicht durch Kombination von Linsen aus unterschiedlichen Materialien. ⇔ Seite 23 Teil 32 Optische Abbildungen 32.4 Optische Instrumente (Optical Instruments) Das Auge Schnittbild des menschlichen Auges Stäbchen (für das Dämmerungssehen) und Zäpfchen (für das Farbsehen) Ziliarmuskel Form der Augenlinse durch Ziliarmuskel veränderbar, im entspannten Zustand maximale Brennweite ca. 2.5 cm = Abstand Hornhaut - Netzhaut ⇒ je näher der Gegenstand, desto stärker die Krümmung der Augenlinse ⇔ Verringerung der Brennweite (Akkomodation). Nahpunkt (deutliche Sehweite) ⇔ ein dem Auge näher gebrachter Gegenstand wird gerade noch scharf wahrgenommen, altersabhängig, Standardwert 25 cm. Ein neuronales Netz bestehend aus 1920 Sensoren zur Bilderkennung bei Roboter Seite 24 Teil 32 Optische Abbildungen Beispiel 32.13: Die Brennweite des Systems Hornhaut-Linse Gesucht: Brennweitenveränderung der Augenlinse, wenn ein Gegenstand aus großer Entfernung zum Nahpunkt (25 cm) bewegt wird ⇒ 1 1 1 aus Abbildungsgleichung Gl. (32.12) + = ⇒ für g = ∞ ⇒ b = f = 2.5 cm, g b f 1 1 1 1 11 + = ⇒ = ⇒ f = 2.27 cm ⇒ für g = 25 cm und b = 2.5 cm ⇒ f 25 cm 25 cm 2.5 cm f Δf = 2.27 cm - 2.5 cm = −0.23 cm Weitsichtiges Auge ⇒ Korrektur mittels Sammellinse Kurzsichtiges Auge ⇒ Korrektur mittels Zerstreuungslinse Astigmatismus: liegt vor, wenn das System Hornhaut-Linse nicht kugelförmig ist, sondern in unterschiedlichen Ebenen verschieden starke Krümmungen aufweist ⇒ Bild eines punktförmigen Gegenstands als ku rze Linie ⇒ Korrektur mit eher zylindrisch gestaltete Brillengläsern. Seite 25 Teil 32 Optische Abbildungen Die Größe, in der uns ein Gegenstand erscheint, entspricht der Bildhöhe auf der Netzhaut ⇒ y' y aus φ = und θ = mit nLuft sinθ = nAuge sinφ ⇒ für kleine Winkel 2.5 cm g y y' 2.5 cm y = nAuge ⇒ y'= θ = nAugeφ ⇒ ∼y nAuge g g 2.5 cm Beispiel 32.14: Lesebrillen Nahpunkt einer Person ohne Brille 75 cm, mit Brille 25 cm ⇔ die Brille erzeugt von einem Gegenstand in 25 cm Entfernung ein virtuelles Bild 75 cm vor der Linse; gesucht: a) Brechkraft der Brille, b) Vergrößerung, c) auf welche der beiden Arten entsteht das größere Bild auf der Netzhaut? f = 37.5 cm f = 37.5 cm Teil a) Wirkung der Sammellinse: g = 25 cm, b = −75 cm ⇒ 1 1 1 1 1 1 1 2 + = ⇒ + = ⇒ = b g f 25 cm −75 cm f f 75 cm ⇒ D = 2.67 dpt bzw. f = 37.5 cm Seite 26 Teil b) Vergrößerung m = − b − 75 cm =− =3 g 25 cm Teil 32 Optische Abbildungen Die Lupe Die scheinbare Größe eines Gegenstands kann mit Hilfe einer Sammellinse vor dem Auge gesteigert werden ⇔ Lupe: Sammellinse, die man vor dem Auge hält, wobei g < f ⇒ die Linse erzeugt ein virtuelles Bild beim Nahpunkt des Auges. b y' ⇒ Bildhöhe y ' = my g y ⇒ Winkel θ , unter dem das Bild dem Auge erscheint Mit Vergrößerung m = näherungsweise: θ = g = b b y my y = = b g b g Gegenstand im Nahpunkt erscheint unter Winkel θ0 ≈ y xnp Gegenstand befindet sich im Brennpunkt der Linse ⇒ die Lichtstrahlen treffen parallel auf das Auge ⇒ das Bild kann mit dem entspannten Auge betrachtet werden ⇒ wenn f < xnp , dann erlaubt die Sammellinse den Gegenstand näher an das Auge zu heranführen ⇒ y vergrößert sich ⇒ Bildhöhe auf der f Netzhaut vergrößert sich. Sehwinkel θ = Winkelvergrößerung oder Vergrößerung der Lupe: m = xnp θ = f θ0 Beispiel 32.15: Winkelvergrößerung einer einfachen Lupe mögliches Prüfungsbeispiel Seite 27 Teil 32 Optische Abbildungen Das Mikroskop Schema eines aus zwei Sammellinsen bestehenden Mikroskops ⇒ Objektiv: erzeugt ein reelles, vergrößertes und umgekehrtes Zwischenbild; Okular: dient als Lupe, mit der das Zwischenbild betrachtet wird ⇔ das Zwischenbild befindet sich im Brennpunkt des Okulars ⇒ die Lichtstrahlen treten parallel aus dem Okular Tubuslänge aus tanβ = y y' =− fo L ⇒ Vergrößerung des Objektivs mo = mit Vergrößerung des Okulars Me = xnp fe y' L =− , y fo ⇒ Gesamtvergrößerung M Beispiel 32.16: Das Mikroskop Mikroskop mit Objektivlinse fo = 1.2 cm und Okularlinse fe = 2 cm, die 20 cm voneinander liegen; gesucht: a) Vergrößerung für ein Nahpunkt xnp = 25 cm, b) Lage des Gegenstandes für Endbild im Unendlichen ⇒ Teil a) aus Gl. (32.22) M = − M=− L xnp fo fe mit L = 20 cm − fo − fe = 20 cm − 1.2 cm − 2 cm = 16.8 cm ⇒ 16.8 cm 25 cm L xnp =− = −175 1.2 cm 2 cm fo fe Teil b) aus Gl. (32.12) 1 1 1 mit b = fo + L = 1.2 cm + 16.8 cm = 18.0 cm ⇒ + = g b fo 1 1 1 1 1 1 = ⇒ = − = 0.778 cm-1 ⇒ g = 1.29 cm + g 1.2 cm 18.0 cm g 18.0 cm 1.2 cm Seite 28 Teil 32 Optische Abbildungen Das Teleskop Mit dem Teleskop werden Gegenstände betrachtet, die weit entfernt sind; Wirkung des Teleskopes: es wird ein reelles Bild des Gegenstands erzeugt, das dem Betrachter viel näher ist als der Gegenstand. Die Vergrößerung des Teleskops ist gleich der erzielten Winkelvergrößerung θ e θo ⇒ mit tanθ o = und tanθ e = y' ≈ θe fe y y' =− ≈ θo g fo ⇒ da y ' < 0 ⇔ Bild ist umgekehrt ⇒ Vergrößerung des Teleskops M Bei dieser Anordnung befindet sich der Beobachtungsbereich hinter dem Objektivspiegel. Spiegelteleskop mit Konkavspiegel als Objektiv Seite 29 Teil 32 Optische Abbildungen Galileis Teleskop, 17. Jahrhundert Hubble Weltraumteleskop http://astro.uchicago.edu/yerkes/index.html Very Energetic Radiation Imaging Telescope Array System http://hubblesite.org/ European Southern Observatory Yerkes Observatory Herschels Teleskop, 1780 http://veritas.sao.arizona.edu/ http://www.eso.org/ Seite 30 Keck Observatory http://www.keckobservatory.org/ Teil 32 Optische Abbildungen Seite 31 Teil 32 Optische Abbildungen Seite 32 Teil 32 Optische Abbildungen Alonso-Finn Physics 32. Reflexion, Brechung und Polarisation 32.1 Einführung 32.2 Strahlen und Wellenoberflächen 32.3 Reflexion und Brechung von ebenen Wellen 32.4 Reflexion und Brechung von Kugelwellen 32.5 Reflexion und Transmission von transversalen Wellen auf einer Saite 32.6 Reflexion und Brechung von elektromagnetischen Wellen 32.7 Ausbreitung von elektromagnetischen Wellen in einem anisotropen Medium 32.8 Reflexion und Brechung an metallischen Oberflächen 33. Wellengeometrie 33.1 Einführung 33.2 Reflexion an einer sphärischen Oberfläche 33.3 Brechung an einer sphärischen Oberfläche 33.4 Linsen 33.5 Optische Instrumente 33.6 Das Prisma 33.7 Dispersion 33.8 Chromatische Aberration Seite 33











