Vorlesung 8

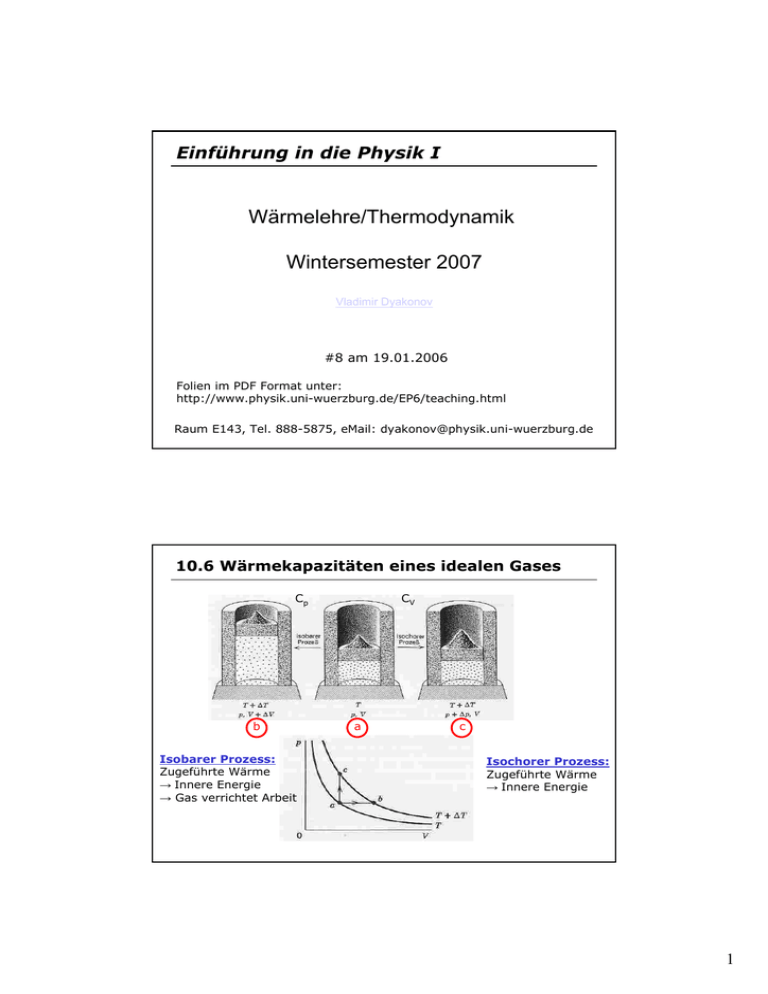
Einführung in die Physik I
Wärmelehre/Thermodynamik
Wintersemester 2007
Vladimir Dyakonov
#8 am 19.01.2006
Folien im PDF Format unter:
http://www.physik.uni-wuerzburg.de/EP6/teaching.html
Raum E143, Tel. 888-5875, eMail: [email protected]
10.6 Wärmekapazitäten eines idealen Gases
CV
Cp
b
Isobarer Prozess:
Zugeführte Wärme
→ Innere Energie
→ Gas verrichtet Arbeit
a
c
Isochorer Prozess:
Zugeführte Wärme
→ Innere Energie
1
10.6 Wärmekapazitäten eines idealen Gases
Bei dem Vergleich der molaren Wärmekapazitäten von Gasen fallen
eine Reihe von Besonderheiten ins Auge:
1) Cp & CV besitzen jeweils für einatomige, zweiatomige und
mehratomige Gase charakteristische Werte
2) Erstaunlich:
Differenz Cp-CV ist bei nahezu allen Gasen eine
Zahl nahe bei R, der allg. Gaskonstante
f=3
f=5
f=7
10.6 Energieerhaltungssaz
2
10.6 Wärme & Arbeit
Beispiel: Gas in einem Behälter
Arbeit
F = p· A
-Gas dehnt sich gegen den Stempeldruck aus
r r
dW = F ⋅ ds = pAds = pdV
Reibungsfreier
Kolben
Isolierende
Wand
p
-Verrichtete ges. Volumensänderungsarbeit:
W = ∫ dW =
Ve
∫ pdV
Wärme
Va
Wärmereservoir
T
10.6 Einschub: äußere/innere Arbeit an Gasen
pi =
pa =
pa> pi
Pa< pi
pa
Reibungsfreier
Kolben
innere Gasdruck
beliebiger Aussendruck
Kompression
Expansion
Verrichtete Arbeit in jedem Fall immer:
V
dW = − pa dV
(„Unendlich langsamer“) Spezialfall pa≈pi:
pi
dW = − pa dV = pi dV
Vorteil: Man kann für pa ≈pi die
Zustandsgleichung verwenden
Fazit: Begrifflich ist zwischen pa und pi streng zu unterscheiden; es besteht
nur numerische Gleichheit zwischen beiden Drücken!
3
10.6 Einschub: äußere/innere Arbeit an Gasen
V2
W = − ∫ pa dV
p a = const .
V2
= − pa ∫ dV = − pa (V2 − V1 )
V1
V1
Konvention: dV < 0; dW > 0
dV > 0; dW < 0
Fläche u. d. Kurve
Geleistete mechanische Arbeit ist wegabhängig und nicht allein durch
die Zustandsgrößen des Anfangs- und Endzustands bestimmt. W ist
keine Zustandsgröße !
10.6 Wärme & Arbeit
Beispiel: Gas in einem Behälter
Isotherme Zustandsänderung
p
pa
p
1
a
Anfangszustand
pa
1
Isotherme
2
pe
Endzustand
Isotherme
Va
Ve
V
pe
b
Va
2
Isotherme
Ve
V
Die von einem System geleistete Arbeit (gelieferte, empfangene
Wärme) hängt nicht nur vom Ausgangs- und Endzustand ab,
sondern auch von den Zwischenzuständen, also vom Weg, auf dem
das System geführt wird
4
10.6 Wärme & Arbeit
Beispiel: Gas in einem Behälter
p
Arbeit ist das Integral unter dem Weg im pV-Diagramm
p
p
a
a
pa
1
pe
pa
b
Va
2
pe
Isotherme
Ve
V
a
1
Va
pa
b
2
1
pe
Isotherme
Ve
V
b
Va
2
Ve
Isother
e
V
10.6 Molare Wärmekapazitäten bei konst. Volumen
- Erwärmung bei konstantem Volumen kann nur erreicht werden,
wenn man gleichzeitig den äußeren Druck erhöht
• Wärmeenergie wird nur in innere Energie umgesetzt
∆Q = ∆U
• Für ein Mol des Gases gilt:
∆Q = cνV · ∆T = ∆U
5
10.6 Molare Wärmekapazitäten bei konst. Druck
- Um eine Erwärmung bei konstantem Druck zu erreichen, muss man
das Gas sich ausdehnen lassen
- Bei Zufuhr an Wärmeenergie erhöht sich das Volumen
(Festkörper, Gas, Flüssigkeit)
• Wärmeenergie wird
(1) in innere Energie umgesetzt und es wird
(2) mechanische Arbeit verrichtet
∆Q = ∆U + ∆Wmech
• ∆Wmech= F ∆x = p A ∆x = p ∆V
• Für ein Mol des Gases gilt:
∆Q = cνV · ∆T + p ∆V
10.6 Molare Wärmekapazitäten bei konst. Druck
• Allg. Gasgleichung für ein Mol des Gases:
vor Expansion:
pV=RT
nach Expansion:
p (V+∆V) = R (T+∆T)
Subtraktion:
p ∆V = R ∆T
• daraus folgt:
∆Q = cνV · ∆T + p ∆V
= cνV · ∆T + R ∆T
cνp
=(cνV + R) ∆T = cνp ∆T
= molare Wärmekapazität bei konstantem Druck
(= cmol, oder cm in d. Literatur)
CνP=CνV+R
6
10.7 Hauptsätze der Thermodynamik
Vorbemerkungen:
•
Thermodynamisches System: System von
Atomen/Molekülen, das mit der Umgebung im
Energieaustausch in Form von Wärme und/oder
mechanischer Arbeit steht.
•
Hauptsätze der Thermodynamik behandeln die Frage:
Wie ändert sich der Zustand eines Systems beim
Energieaustausch mit der Umgebung ?
•
Die Hauptsätze der Thermodynamik sind mathematisch nicht
beweisbar, sondern Erfahrungstatsachen, die aus
Beobachtungen abgeleitet sind.
•
Zustand eines Systems: Gesamtheit seiner Eigenschaften,
die durch äußere Randbedingungen festgelegt sind.
•
Gleichgewichtszustand eines Systems: Eigenschaften
ändern sich nicht mit der Zeit (stationärer Zustand)
•
Gleichgewichtszustand des Systems eindeutig bestimmt
durch die Zustandsgrößen: P, V, T
10.7 1. Hauptsatz der Thermodynamik
Nebenbemerkungen: Zustandsfunktion
•
•
Man ändere den Zustand eines Systems vom Zustand
A nach Zustand B so langsam, dass immer
thermodynamisches Gleichgewicht herrscht.
Dann hängt die dabei zugeführte Wärmemenge ∆Q
von der Vorgehensweise bei der Zustandsänderung ab
(Wegabhängigkeit von ∆Q )
Auch die aufgewendete Arbeit ∆W hängt vom Weg ab
•
d.h. Q, W sind Wegfunktionen
•
Die Änderung der Inneren Energie ∆U hängt aber nur
vom Startpunkt (Zustand A) und vom Endpunkt
(Zustand B) ab (wegunabhängig).
•
U nennt man deshalb eine Zustandsfunktion
7
10.7 1. Hauptsatz der Thermodynamik
Veranschaulich:
pa
1
- System geht von 1 nach 2
(irgendwie)
Anfangszustand
- System leistet W/ empfängt Q
Isotherme
2
pe
Endzustand
Isotherme
Va
Ve
V
- Q & W sind wegabhängig, d.h.
prozessabhängig !
- Innere Energie U = Q+W ist
wegunabhängig
- U hängt nur vom Anfangs& Endzustand ab, wobei beide
Gleichgewichtszustände sind
10.7 1. Hauptsatz der Thermodynamik
Die einem System von außen zugeführte Wärmemenge ∆Q führt zu
•
•
Erhöhung ∆U der inneren Energie U und damit Erhöhung ∆T
der Temperatur T
Expansion des Volumens V gegen den äußeren Druck, wobei
vom System die Arbeit ∆W verrichtet wird
Gleichung des 1. Hauptsatzes:
∆Q = ∆U - ∆W
• 1. Haupsatz ist der Energieerhaltungssatz der Thermodynamik:
∆U = ∆Q + ∆W
Summe der einem System von außen zugeführten Wärme und der
zugeführten Arbeit ist gleich der Zunahme der inneren Energie
8
10.7 1. Hauptsatz der Thermodynamik
dU = δ Q + δ W
Differentielle Form des 1. Hauptsatzes
Vorzeichenkonvention:
Dem System zugeführte Energie δQ und am System geleistete Arbeit
δW werden positiv gezählt, entzogene Energien und abgegebene
Arbeit erscheinen negativ
(NB: Vorzeichenkonvention ist leider nicht einheitlich in der Literatur)
• Der 1. Hauptsatz kann auf jeden Vorgang in der Natur angewendet
werden, sofern er nur zwischen 2 Gleichgewichtszuständen stattfindet
• Eine periodisch arbeitende Wärmekraftmaschine (Dampfmaschine,
Ottomotor) hat nach einem Arbeitszyklus im Idealfall ihre innere
Energie ∆U nicht geändert, ∆U = 0, ⇒ ∆Q = -∆W :
• „Es ist unmöglich, eine periodisch arbeitende Maschine zu bauen,
die ohne Energiezufuhr ∆Q ständig Arbeit ∆W verrichtet“.
• Unmöglichkeit eines „Perpetuum mobile 1. Art“
10.7 1. Hauptsatz der Thermodynamik
Robert Mayer 1814-1878 (Mediziner)
Als er eines Tages nach Indonesien reiste bemerkte er, dass in dem tropischen
Klima das Venenblut eine dem arteriellen Blut ähnliche Färbung annahm. Durch
diese Beobachtung angeregt, begann er mit einer Untersuchung des
menschlichen Wärmehaushalts. Seine Ergebnisse fasste er zum
Ersten Hauptsatz der Thermodynamik zusammen:
Energie kann nicht
vernichtet werden.
Sie kann lediglich
in eine andere
Form von Energie
umgewandelt
werden.
Man kann keine Maschine
konstruieren (Perpetuum
Mobile erster Art), die
nichts weiter tut als
Energie zu erzeugen.
Mayers Theorie wurde jedoch nicht anerkannt, da Beweise fehlten. Erst Joule
konnte diese Theorie wenig später und unabhängig von Mayer genauer
nachweisen. Erst Jahre später wurde Mayer nach schweren Depressionen und
einem Selbstmordversuch auch als Entdecker anerkannt und erhielt viele
Auszeichnungen und wurde sogar in den Adel aufgenommen (von Mayer).
9
10.7 Formulierungen des 1. Hauptsatzes
• Energiesatz der Mechanik beantwortet die Frage, wie sich die
Energie eines mechanischen Systems ändern läßt: durch Arbeit
∆W= ∆E = ∆(Etr + Erot + Ep + Eschw)
Energie eines mechanischen Systems kann durch Zufuhr bzw. Abfuhr
von Arbeit geändert werden.
• In der Thermodynamik wird die Energieübertragungsform „Wärme“
ins Geschehen mitaufgenommen:
∆U = ∆Q + ∆W
Die innere Energie U eines thermodynamischen Systems kann durch
Zufuhr von Arbeit ∆W oder durch Zufuhr von Wärme ∆Q vergrößert
werden (1. Hauptsatz)
Energiezufuhr: mechanischen, elektrischen, magnetischen Weg;
Strahlung
10.7 Formulierungen des 1. Hauptsatzes
•
•
•
Wärme und Arbeit sind Übertragungsformen der Energie.
Im System selbst steckt dann weder Arbeit noch Wärme; nur die
Energie (innere Energie) des Systems hat sich bei der Übertragung
geändert.
Deswegen ist es falsch zu sagen: Wärme wird im System
gespeichert (Wärmekapazität)
Formen der Energieübertragung:
1) Mechanische Volumenarbeit: dW =- pdV; (Kolben)
2) Wärme: dQ= CV dT; (Flamme, Wärmebad, Heizspirale)
Konvention:
Positive ∆W, ∆Q
Negative ∆W, ∆Q
⇔
⇔
Vergrößerung der inneren Energie
Verkleinerung der inneren Energie
10
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
Beispiele zum ersten Hauptsatz
Genauere Betrachtung der möglichen Zustandsänderungen, die jeweils
nach der primären Zustandsvariablen, die sich bei dem Prozess nicht
ändert, klassifiziert werden
1) Isochore Prozesse
∆V = 0 Î
V = konstant
2) Isobare Prozesse
∆p = 0 Î
p = konstant
3) Isotherme Prozesse
∆T = 0 Î
T = konstant
4) Adiabatische Prozesse
∆Q = 0 Î
S = konstant
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
a) Isochorer Prozesse (V = constant)
Isochore Zustandsänderung bedeutet, der Stempel bleibt in Ruhe
∆V = 0
Î
dx = 0
Î
∆W = 0
d.h. es wird keine äußere Arbeit verrichtet
11
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
a) Isochorer Prozesse (V = constant)
Die von außen dem System zugeführte Wärmemenge dQ wird
vollständig in innere Energie dU umgesetzt (Temperaturerhöhung)
∆Q = ∆U
= CV ∆Τ
Definitionsgleichung:
Spezifische
Wärmekapazität bei
konstantem Volumen
⎛ ∂U ⎞
CV = ⎜
⎟
⎝ ∂T ⎠V
Verbindet stoffcharakteristische Größe mit Zustandsgrößen
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
b) Isobarer Prozess (p = constant)
Die von außen dem System zugeführte Wärmemenge dQ wird in
Arbeit dW und innere Energie dU umgewandelt
∆Q = ∆U
+ ∆W
12
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
b) Isobarer Prozess (p = constant)
Bei Wärmezufuhr unter konstantem Druck dehnt sich das Gas aus und
verrichtet mechanische Arbeit
∆W = F ∆x
= p A ∆x
= p ∆V
∆Q = ∆U + p ∆V = cp m ∆T
cp: Wärmekapazität eines Gase bei konstantem Druck.
•
Neue Zustandsgröße: Enthalpie H
H = U + p V (Zustandsgröße)
dH = dU + p dV + dp V = dU + p dV = dQ
⎛ ∂H ⎞
CP = ⎜
⎟
⎝ ∂T ⎠ P
Bei isobarer Zustandsänderung ist die Enthalpiezunahme gleich
der zugeführten Wärmemenge
Zustandsgröße H wird oft verwendet bei Phasenumwandlungen,
chemischen Reaktionen oder anderen Prozessen, die mit p = const.
ablaufen
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
c) Isothermer Prozess (T = constant)
•
Weil U ~ T: dU ≡ 0 !
∆Q = ∆W
•
dQ = p dV
Die von außen dem System zugeführte Wärmemenge dQ wird
vollständig in Arbeit dW umgewandelt, die das System wieder nach
außen abgibt.
•
Arbeitsleistung bei isothermer Zustandsänderung (Ausdehnung: d.h.
V1 < V2):
p ⋅ V = R ⋅ T = const.
W =Q=
V2
V2
V1
V1
1
V2
∫ p(V )dV = RT ∫ V dV = RT ln V
1
13
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
c) Isothermer Prozess (T = constant)
•Da U ~ T: dU ≡ 0 ! (Innere Energie ändert sich nicht,
wohl aber die Energiedichte !!!)
p
p1
∆Q = ∆W
1
• dQ = p dV
Die von außen dem System zugeführte
Wärmemenge dQ wird vollständig in
Arbeit dW umgewandelt, die das System
wieder nach außen abgibt.
2
p2
V1
V2
W =Q=
V
V2
• Arbeitsleistung bei isothermer Zustandsänderung
(Ausdehnung: d.h. V1 < V2):
V2
V
1
dV = RT ln 2
V
V1
V1
∫ p(V )dV = RT ∫
V1
10.7 Anwendungen des 1. Hauptsatz der Thermodynamik
d) Adiabatischer Prozess (Q = constant)
∆U = ∆W
•
dQ ≡ 0 !
•
Hierbei findet kein Austausch von Wärmeenergie mit der
Umgebung statt !
bei schnellen Änderungen von V, p (Wärmeaustausch hängt nach)
bei thermischer Isolation
-
T
Thermische Isolation
Luftpumpe
14