5. ¨Ubung (KW 48)

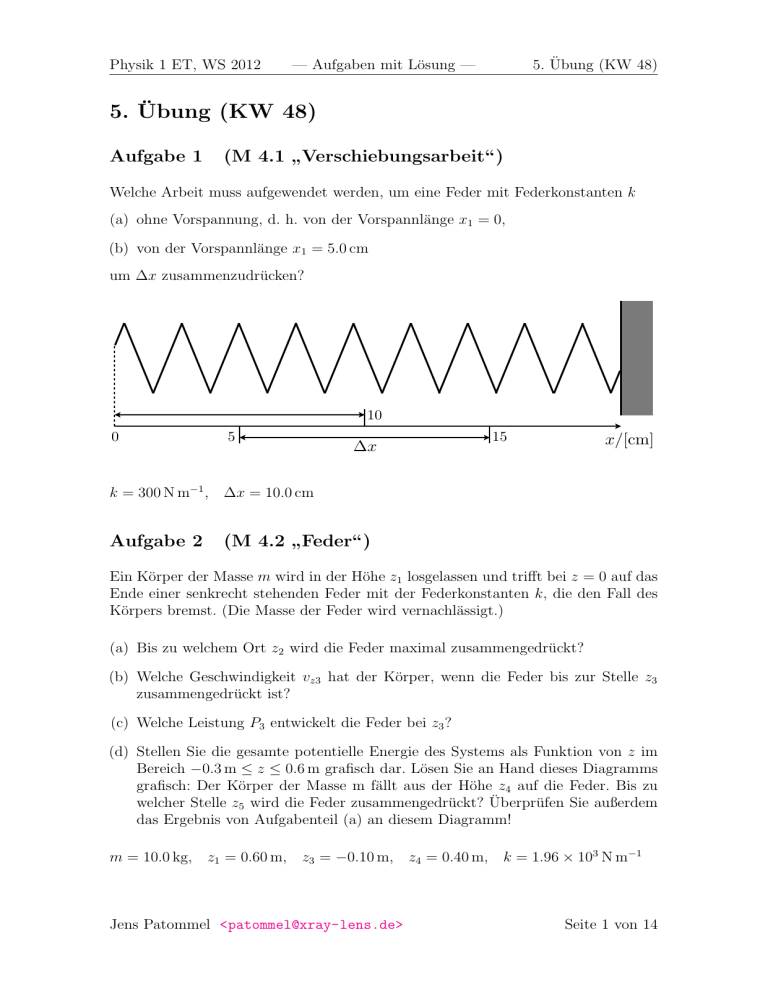
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
5. Übung (KW 48)
Aufgabe 1
(M 4.1 Verschiebungsarbeit“)
”
Welche Arbeit muss aufgewendet werden, um eine Feder mit Federkonstanten k
(a) ohne Vorspannung, d. h. von der Vorspannlänge x1 = 0,
(b) von der Vorspannlänge x1 = 5.0 cm
um ∆x zusammenzudrücken?
10
0
5
x
15
x/[cm]
k = 300 N m−1 , ∆x = 10.0 cm
Aufgabe 2
(M 4.2 Feder“)
”
Ein Körper der Masse m wird in der Höhe z1 losgelassen und trifft bei z = 0 auf das
Ende einer senkrecht stehenden Feder mit der Federkonstanten k, die den Fall des
Körpers bremst. (Die Masse der Feder wird vernachlässigt.)
(a) Bis zu welchem Ort z2 wird die Feder maximal zusammengedrückt?
(b) Welche Geschwindigkeit vz3 hat der Körper, wenn die Feder bis zur Stelle z3
zusammengedrückt ist?
(c) Welche Leistung P3 entwickelt die Feder bei z3 ?
(d) Stellen Sie die gesamte potentielle Energie des Systems als Funktion von z im
Bereich −0.3 m ≤ z ≤ 0.6 m grafisch dar. Lösen Sie an Hand dieses Diagramms
grafisch: Der Körper der Masse m fällt aus der Höhe z4 auf die Feder. Bis zu
welcher Stelle z5 wird die Feder zusammengedrückt? Überprüfen Sie außerdem
das Ergebnis von Aufgabenteil (a) an diesem Diagramm!
m = 10.0 kg, z1 = 0.60 m, z3 = −0.10 m, z4 = 0.40 m, k = 1.96 × 103 N m−1
Jens Patommel <[email protected]>
Seite 1 von 14
Physik 1 ET, WS 2012
Aufgabe 3
— Aufgaben mit Lösung —
5. Übung (KW 48)
(M 4.7 Bus“)
”
Ein vollbesetzter Bus hat die Masse m.
(a) Welche Arbeit W10 bringt der Motor bei jedem Anfahren bis zum Erreichen der
Geschwindigkeit v1 auf ebener Straße auf?
(b) Welche maximale Leistung P1 und welche durchschnittliche Leistung P̄ wären
erforderlich, wenn das Anfahren auf einer ebenen Strecke s1 gleichmäßig beschleunigt erfolgen würde?
m = 10 t, v1 = 30 km h−1 , s1 = 100 m
Aufgabe 4
(M 4.8 Schleifenbahn“)
”
Ein Körper (Masse m) soll, nachdem er von einer Feder (Federkonstante k) abgeschossen wurde, eine Schleifenbahn vom Radius r reibungsfrei durchlaufen.
r
m
(a) Um welches Stück x0 muss man die Feder spannen, damit der Körper die Schleifenbahn gerade noch durchläuft, ohne herunterzufallen?
(b) Wie groß ist die Zwangskraft der Schiene, wenn der Körper gerade in die Kreisbahn eingelaufen ist (F1 ) bzw. die Kreisbahn gerade verlassen hat (F0 )?
m = 20 g, k = 4.8 N cm−1 , r = 0.50 m
Aufgabe 5
(M 4.13 zweite kosmische Geschwindigkeit“)
”
Man berechne die zweite kosmische Geschwindigkeit! (Mit anderen Worten: Mit
welcher Geschwindigkeit v muss ein Körper die Erdoberfläche verlassen, wenn er die
Erdanziehung gerade noch überwinden soll?)
Jens Patommel <[email protected]>
Seite 2 von 14
Physik 1 ET, WS 2012
Aufgabe 6
— Aufgaben mit Lösung —
5. Übung (KW 48)
(M 4.6 Pumpe“)
”
Aus einem Salzbergwerk soll eine Pumpe Salzsole der Dichte ρ auf die Höhe h heben.
Mit welcher Leistung P muss die Pumpe betrieben werden, wenn sie die Stromstärke
I (Volumen durch Zeit) erzeugen soll?
ρ = 1.15 g cm−3 , h = 50 m, I = 360 l min−1
Aufgabe 7
(M 4.10 Kugelrutsch“)
”
Vom höchsten Punkt einer Kugel (Radius r) gleitet eine Punktmasse reibungsfrei
und löst sich an einer bestimmten Stelle von der Kugeloberfläche. Um welchen
Höhenunterschied h liegt diese Stelle tiefer als der höchste Punkt?
m
h
m
r
r
Jens Patommel <[email protected]>
Seite 3 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
Lösung zu Aufgabe 1
Die von der Umgebung an einem System verrichtete Arbeit ist definiert als das
Wegintegral über das Skalarprodukt d~r · F~a (~r) entlang des Weges C, wobei C vom
Punkt A zum Punkt B verläuft und F~ die von außen auf das System ausgeübte
Kraft darstellt:
Z
Z
~
~
WA→B
= d~r · Fa (~r) = dr Fa (~r) cos ^ d~r, Fa (~r) .
C
C
C
Wenn eine Feder zusammengedrückt wird, muss die von der Feder ausgeübte Kraft
F~F kompensiert werden, d. h. von außen muss die Kraft F~a = −F~F aufgebracht
werden. Diese von außen aufgebrachte Kraft verläuft während des gesamten Vorgangs parallel zum Weg (F~a ||d~r) und zeigt stets in dieselbe Richtung wie dieser
(F~a0 = d~r0 ).1 Wird eine Feder, die bei x = 0 entspannt ist, von x1 auf x2 zusammengedrückt, so gilt für die an der Feder verrichtete Arbeit:
Wx1 →x2
Zx1
Zx2
Zx2
= dx Fa (x) cos ^(d~r, ~r) = dx Fa (x) cos(0) = dx kx = 12 k x22 − x21
x0
∆x=x2 −x1
=⇒
x1
2
W∆x (x1 ) = 12 k (x1 + ∆x) −
(a) W0.10 m (0.00 m) =
1
2
x1
x21
2
= 21 k(∆x) + kx1 ∆x = W∆x (0) + kx1 ∆x .
· 300 N m−1 · (0.10 m)2 = 1.5 J
(b) W0.10 m (0.05 m) = W0.10 m (0.00 m) + 300 N m−1 · 0.05 m · 0.10 m = 3.0 J
Lösung zu Aufgabe 2
(a) Die Gesamtenergie Eges setzt sich zusammen aus der potentiellen Energie Eg
im Schwerefeld der Erde, der potentiellen Energie EF der Feder und der kinetischen
Energie Ekin . Am Anfang ist die Feder entspannt und der Körper befindet sich in
Ruhe, deshalb sind die Federenergie und die kinetische Energie am Anfang 0, die
Gesamtenergie beträgt also am Anfang
Eges1 = Eg1 = mgz1 .
Wenn die Feder (bei z2 ) maximal zusammengestaucht ist, ist der Körper in Ruhe,
die kinetische Energie ist dann wiederum Null. Die Gesamtenergie im Zustand der
maximal gestauchten Feder beträgt
Eges2 = Eg2 + EF2 = mgz2 + 21 kz22 .
1
Die Schreibweise ~v 0 verwende ich stellvertretend für den Einheitsvektor, der in dieselbe Richtung weist wie ~v , d. h. ~v 0 ≡ |~~vv| .
Jens Patommel <[email protected]>
Seite 4 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
Es gilt der Energieerhaltungssatz, wonach die Gesamtenergie konstant ist:
⇐⇒
Eges1 = Eges2
=⇒ mgz1 = mgz2 + 21 kz22
mg
mg
z22 + 2
z2 = 2
z1 .
k
k
Diese quadratische Gleichung kann man durch quadratische Ergänzung oder mittels
p-q-Formel nach z2 auflösen:
s
!
mg
kz1
−1 ± 1 + 2
.
z2 =
k
mg
Das positive Vorzeichen bedeutet eine Streckung und das negative Vorzeichung eine
Stauchung der Feder, wobei das positive Vorzeichung nur dann eine gültige Lösung
ergibt, wenn der Körper bei der Aufwärtsbewegung mit der Feder fest verbunden
bleibt (mittels eines Kopplungsmechanismus, zum Beispiel durch Magnetkraft). Ist
der Körper nur lose mit der Feder verbunden, wird er sich von ihr lösen, sobald die
Gleichgewichtslage erreicht ist. Darum brauchen wir uns aber keine Gedanken zu
machen, denn gefragt ist nach der Position der maximalen Federstauchung, nicht
nach der maximalen Streckung. Die Lösung lautet also
s
!
kz1
mg
1+ 1+2
z2 = −
k
mg


s
−1
−2
10 kg · 9.81 m s 
1.96 kN m · 0.6 m 
=−
1+ 1+2
−1
1.96 kN m
10 kg · 9.81 m s−2
= −30.0 cm .
(b) Die Position z3 liegt zwischen z2 und 0, also in jenem Bereich, wo sowohl die
Federenergie als auch die kinetische Energie zur Gesamtenergie beitragen. Nach dem
Energieerhaltungssatz gilt
2
mgz1 = mgz3 + 12 kz32 + 21 mvz3
r
k
⇐⇒ vz3 = ± 2g(z1 − z3 ) − z32
m
s
=±
29.81 m s−2 (0.6 m − 0.1 m) −
(2.1)
1.96 kN m−1
(0.1 m)2
10 kg
= ±3.4 m s−1 .
Das positive Vorzeichen der Geschwindigkeit bedeutet, dass sich der Körper auf dem
Weg nach oben und das negative Vorzeichen, dass sich der Körper auf dem Weg nach
untern befindet.
Jens Patommel <[email protected]>
Seite 5 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
(c) Die Leistung ist die Zeitableitung der Arbeit bzw. Energie, die Momentanleistung der Feder beträgt somit
1 dz(t)2
dWF (t)
d 1
2
kz(t) = 2 k
PF (t) =
=
dt
dt 2
dt
2
KR 1 dz dz(t)
= 2k
= 12 k · 2z(t) · vz (t)
dz dt
r
k
(2.1)
= kz(t) vz (t) = ±kz(t) 2g [z1 − z(t)] − z(t)2 ,
| {z }
m
FF (z(t))
wobei ich die Kettenregel df (g(x))
= dfdg(g) dg(x)
und Gleichung (2.1) mit z3 ≡ z(t)
dx
dx
verwendet habe. Zum Zeitpunkt t3 mit z3 = z(t3 ) entwickelt die Feder die Leistung
P3 = PF (t3 )
r
k
= ±kz(t3 ) 2g [z1 − z(t3 )] − z(t3 )2
m
r
k
= ±kz3 2g [z1 − z3 ] − z32
m
= ±1.96 kN · 0.1 m · 3.4 m s−1
= ±0.67 kW .
E/J
Epot
Eges1
50
Ekin,max
Ekin (z3 )
Eges2
10
z2 z5
z3
0.1
z4
0.5
z1
z/m
10
Jens Patommel <[email protected]>
Seite 6 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
E/J
Eges
50
Epot
Ekin
10
z3
z2
0.1
z1
0.5
z/m
10
E/J
Eges
50
Epot
EF
Ekin
10
z3
z2
0.1
0.5
10
z1
z/m
Eg
Lösung zu Aufgabe 3
(a) Die vom Motor zum Anfahren des Busses zu verrichtende Arbeit ist die Differenz aus kinetischer Energie Ekin1 nach Erreichen der Geschwindigkeit v1 und der
kinetischen Anfangsenergie Ekin0 :
W10 = Ekin1 − Ekin0 = 12 mv12 − 0 = 347 kJ .
Jens Patommel <[email protected]>
Seite 7 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
(b) Die momentane Leistung P (t) berechnet sich aus der Zeitableitung der zur
Beschleunigung verrichteten Arbeit, also der kinetischen Energie:
dW 0 (t)
dt
d 1
2
mv(t)
=
dt 2
dv 2 dv(t)
= 21 m
dv dt
1
= 2 m · 2v(t) · a(t)
= m v(t) a(t)
= ma0 v(t) .
P (t) =
(3.1)
Im letzten Schritt wird ausgenutzt, dass die Beschleunigung konstant erfolgt. Wir
suchen das Maximum der Leistung im Zeitintervall [0, t1 ]. Dazu bilden wir die erste
Zeitableitung:
dP (t)
d
=
ma0 v(t)
dt
dt
dv(t)
= ma0
dt
2
= ma0 > 0 .
Die Zeitableitung der Leistung ist für alle t positiv, P (t) ist somit eine streng monoton wachsende Funktion und hat ihr Maximum am rechten Rand bei t1 . Es gilt
somit für die maximale Leistung:
P1 = P (t1 ) = ma0 v(t1 ) = ma0 v1 .
(3.2)
Die Beschleunigung erhält man aus der Bewegungsgleichung für konstante Beschleunigung
v(t) = a0 t,
s(t) = 12 a0 t2 ,
indem man dort die Zeit t1 einsetzt:
v1 = a0 t1 ,
s1 = 12 a0 t21
und t1 eliminiert:
t1 =
v1
a0
=⇒
s1 =
1
a
2 0
⇐⇒
a0 =
2
1 v1
2
s1
(3.3)
v1
a0
2
(3.4)
Dies setzen wir in (3.2) ein und erhalten für die maximale Leistung
P1 = ma0 v1 = 21 m
v13
= 28.9 kW.
s1
Jens Patommel <[email protected]>
Seite 8 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
Den zeitlichen Mittelwert hgi[t0 ,t1 ] einer physikalischen Größe g(t) über ein Zeitintervall [t0 , t1 ] definiert man ganz allgemein als folgendes Integral:
hgi[t0 ,t1 ]
1
=
t1 − t0
Zt1
dt g(t).
t0
Dies wenden wir an, um die durchschnittliche Leistung beim Beschleunigen des
Busses zu bestimmen, wobei wir beachten, dass die Leistung als Zeitableitung der
Arbeit definiert ist:
1
P̄ =
t1 − t0
1
=
t1 − t0
1
=
t1 − t0
Zt1
dt P (t)
t0
Zt1
dW
dt
dt
t0
W
Z(t1 )
dW
W (t0 )
W (t1 ) − W (t0 )
t1 − t0
1
mv 2
= 2 1.
t1
=
Die Zeit t1 wird errechnet, indem wir (3.4) in (3.3) einsetzen,
(3.4) ∧ (3.3)
=⇒
t1 = 2
s1
,
v1
so dass wir für die Durchschnittsleistung schlussendlich erhalten:
P̄ = 41 m
v13
= 12 P1 = 14.45 kW .
s1
Lösung zu Aufgabe 4
Bei dieser Aufgabe wird vorausgesetzt, dass der Körper auf der Fahrbahn lose aufliegt, so dass die Zwangskraft, die die Fahrbahn auf den Körper ausübt, immer nur
abstoßend ist, niemals anziehend (anders als bei einer Achterbahn, bei der die Räder
der Waggons von den Führungssschienen fest umschlossen sind). Für den Looping
bedeutet dies, dass die Zwangskraft immer nur zum Kreismittelpunkt wirken kann,
nicht aber vom Mittelpunkt weg. Daraus ergibt sich die Bedingung dafür, dass der
Körper eine vollständige Schleifenbahn durchführt, nämlich dass die dafür erforderliche Zwangskraft der Fahrbahn immer nur zum Mittelpunkt weisen oder bestensfalls
Null sein darf.
Jens Patommel <[email protected]>
Seite 9 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
(a) Wir berechnen die für die Schleife erforderliche Zwangskraft, indem wir die
Radialkomponente der Gravitationskraft bestimmen:
F~g,r = (F~g~er )~er
= (−mg~ez~er )~er
= [−mg~ez (cos α ~ex + sin α ~ez )] ~er


= −mg cos α ~ez~ex −mg sin α ~ez~ez  ~er
|{z}
|{z}
=0
=1
= −mg sin α ~er .
Die Radialkomponente der Zentripetalkraft beträgt
2
v
F~r = −m ~er ,
r
so dass für die Radialkomponente der Zwangskraft
v2
v2
~
~
~
FZ,r = Fr − Fg,r = −m ~er + mg sin α ~er = mg sin α − m
~er
r
r
(4.1)
folgt. Da die Zwangskraft nur abstoßend wirkt, muss der Klammerausdruck negativ
oder Null sein (Zwangskraft in Richtung Mittelpunkt, wohingegen ~er vom Mittelpunkt weg zeigt). Wir fordern also
v2
≤0
r
1
mv 2 ≥ 12 mgr sin α
2
mg sin α − m
⇐⇒
sin α≤1
1
mv 2
2
=⇒
≥ 12 mgr
Der Looping wird gerade so durchlaufen, wenn das Gleichheitszeichen gilt:
1
mv 2
2
= 12 mgr
(4.2)
Über den Energieerhaltungssatz kann man nun ausrechnen, wie stark die Feder
gespannt werden muss:
1
kx2
2
= 12 mv 2 + mgh
h=2r 1
= 2 mv 2 + 2mgr
(4.2) 1
= 2 mgr + 2mgr
= 25 mgr
r
=⇒ |x| =
5
mgr
=
k
r
5
(4.3)
20 g · 9.81 m s−2 · 0.5 m
= 3.2 cm .
4.8 N cm−1
(b) Wenn der Körper die Schleife gerade verlassen hat, bewegt er sich mit konstanter
Geschwindigkeit unbeschleunigt fort, die Gesamtkraft F~ges = F~g + F~Z0 ist also Null,
so dass die Zwangskraft
F~Z0 = −F~g = mg ~ez = 20 g · 9.81 m s−2 ~ez = 196 mN
Jens Patommel <[email protected]>
Seite 10 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
beträgt.
Wenn der Körper die Schleifenbahn gerade betreten hat, ist die Radialkomponente
durch (4.1) gegeben mit α = −90°. Weil die Zwangskraft immer nur senkrecht zur
Bahnebene wirkt, ist ihre Tangentialkomponente Null, und somit folgt
2
v
(4.1)
~er
F~Z1 = F~Z,r1 = mg sin α − m
r
v2
= mg sin α − m
[cos α ~ex + sin α ~ez ]
r


 
2
v
α=−90°
= mg sin(−90°) −m  cos(−90°) ~ex + sin(−90°) ~ez 
| {z }
| {z }
| {z }
r
=−1
=0
=−1
2
v
= mg + m
~ez .
(4.4)
r
Die Geschwindigkeit am Schleifeneingang berechnen wir mit dem Energieerhaltungssatz 12 mv 2 = 21 kx2 unter berücksichtigung von (4.3):
1
mv 2
2
2
⇐⇒
(4.4)
=⇒
(4.3) 5
mgr
2
= 12 kx2 =
v
= 5g
r
F~Z1 = (mg + 5m) ~ez = 6mg ~ez = 6F~Z0 = 1177 mN .
Lösung zu Aufgabe 5
Wieder haben wir es mit einem schönen Beispiel zu tun, bei dem die Nützlichkeit
des Energieerhaltungssatzes zutage tritt. Ohne EES müsste man die Bewegungsgleichung aufstellen, indem man mit Hilfe des Newtonschen Gravitatinsgesetztes
m1 m2 0
F~1→2 = −F~2→1 = −γ
~r
|~r12 |2 12
die Beschleunigung ~a(t) = r̈(t) berechnet, was bei Wahl eines geeigneten Bezugssystems auf eine Differentialgleichung der Form
z̈(t) = −γ
mE
,
z 2 (t)
z(0) = RE ,
ż(0) = v0
führt (Abschuss des Objektes radial zur Erde in Richtung ~ez , Erdmittelpunkt im Koordinatenursprung). Daraus würde man die Geschwindigkeits-Zeit-Funktion v(t) =
ż(t) ermitteln und v0 so bestimmen, dass für alle endlichen Zeitpunkte v(t) > 0 gilt,
das heißt, dass die Geschwindigkeit erst im Grenzfall t → ∞ Null wird.
Viel eleganter und einfacher ist es jedoch, die Aufgabe mit Hilfe des Energieerhaltungssatzes zu lösen, denn uns intersessiert ja nicht die komplette Flugbahn des
Jens Patommel <[email protected]>
Seite 11 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
Objetks, sondern nur dessen Anfangs- und Endgeschwindigkeiten. Die Energiebilanz
lautet
⇐⇒
Wpot,0 + Wkin,0 = Wpot,1 + Wkin,1
mmE 1 2
mmE 1 2
+ 2 mv0 = −γ
+ 2 mv1
−γ
z0
z1
v1 =0
1
1
z0 =RE
2
−
.
=⇒
v0 = 2γmE
RE z1
(5.1)
Diese Gleichung gibt an, wie groß die Anfangsgeschwindigkeit sein muss, damit das
Geschoss in der Höhe z1 zur Ruhe kommt (Umkehrpunkt). Wir möchten allerdings,
dass das Objekt gar nicht zur Erde zurück kommt, z1 muss also im Unendlichen
liegen. Die zweite kosmische Geschwindigkeit ergibt sich somit als der Grenzert für
z → ∞:
s
r
q
1
1
mE
(5.1)
−
= 2γ
v̂0 =
lim v02 (z1 ) =
lim 2γmE
z1 →∞
z1 →∞
RE z1
RE
s
6 × 1024 kg
= 2 × 6.67 × 10−11 m3 kg−1 s−2
= 11.2 km s−1 .
6.37 × 106 m
Lösung zu Aufgabe 6
Die Leistung der Pumpte ergibt sich als Zeitableitung der von der Pumpe verrichteten Arbeit:
dW (t)
dm(t)gh
dm(t)
dρV (t)
dV (t)
=
= gh
= gh
= ρgh
= ρghI(t)
dt
dt
dt
dt
dt
= 1.15 g cm−3 · 9.81 m s−2 · 50 m · 360 l min−1 = 3.38 kW .
P (t) =
Lösung zu Aufgabe 7
Aus dem Energieerhaltungssatz ergibt sich die Geschwindigkeit des Körpers in der
Höhe h unterhalb des höchsten Punktes:
mgh = 12 mv 2
⇐⇒ v 2 = 2gh .
Jens Patommel <[email protected]>
(7.1)
Seite 12 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
Die Zwangskraft der Unterlage auf den Körper ergibt sich in der Höhe h aus der
Radialbeschleunigung und der Radialkomponente der Gewichtskraft zu
⇐⇒
F~r = F~Z + F~g,r
F~Z = F~r − F~g,r
v2
= −m ~er + [mg ~ez~er ] ~er
r
h
(7.1)
=
−2mg ~er + mg [~ez (cos α ~ex + sin α ~ez )] ~er
r
h
= −2mg ~er + mg [cos α ~ex~ez + sin α ~ez~ez ] ~er
r
h
= −2mg ~er + mg sin α ~er
r
h
= mg sin α − 2
~er .
r
(7.2)
Der Körper hebt ab, sobald die Zwangskraft der Unterlage auf den Körper Null
wird:
(7.2)
⇐⇒
F~Z = 0
h
2 = sin α .
r
(7.3)
m
h
m
↵
r
h
r
↵
Andererseits gilt zwischen dem Winkel α und der Höhe h der geometrische Zusammenhang
r−h
,
r
was wir in (7.3) einsetzen und nach h auflösen:
sin α =
h
r−h
=
r
r
h
h
2 =1−
r
r
1
h = 3r .
2
⇐⇒
⇐⇒
Jens Patommel <[email protected]>
Seite 13 von 14
Physik 1 ET, WS 2012
— Aufgaben mit Lösung —
5. Übung (KW 48)
Quellen
Die Aufgaben sind entnommen aus: Peter Müller, Hilmar Heinemann, Heinz Krämer,
Hellmut Zimmer, Übungsbuch Physik, Hanser Fachbuch, ISBN: 978-3-446-41785-4
http://www.hanser-fachbuch.de/buch/Uebungsbuch+Physik/9783446417854
Die Übungs- und Lösungsblätter gibt es unter
http://newton.phy.tu-dresden.de/~patommel/Physik_1_ET
Die Homepage zur Vorlesung findet sich unter
http://www.iapp.de/iapp/lehre/materialien/?v=pe
Jens Patommel <[email protected]>
14