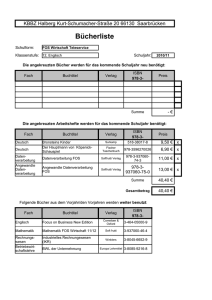
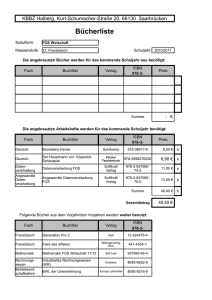
Document

DATENVERARBEITUNG FÜR TPH II
LVA Nr. 138.074
Methoden zur numerischen Lösung
gewöhnlicher Differentialgleichungen
Teil 2
H. Leeb
Inhalt
Gegenstand dieser Vorlesung und den beiden zugehörigen Übungseinheiten sind die
grundlegenden Verfahren zur numerischen Lösung von gewöhnlichen Differentialgleichungen.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Einschrittverfahren für Differentialgleichungen 1. Ordnung
Konsistenz und Konvergenz von Lösungsalgorithmen
Runge-Kutta-Verfahren
Rundungsfehler
Das Numerov-Verfahren
Mehrschrittverfahren (Korrektor- und Prediktorverfahren)
Extrapolationsverfahren
Anwendungen:
• Das Pendel (Übung 1)
• Bindungszustände in einem Zentralpotential (Übung 2)
• Streulösungen der radialen Schrödingergleichung (Übung 2)
• Transmission und Reflexion am eindimensionalen Potentialwall (Übung 2)
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
2
Wiederholung Einschrittverfahren
Explizites Einschrittverfahren:
Aus der Kenntnis der Lösung yh(xi) läßt sich direkt der Wert an der nächsten
Stützstelle yh(xi+1) berechnen [xi,xi+1 sind Stützstellen, h=xi+1-xi Schrittweite]
(
)
y h ( xi +1 ) = y h ( xi ) + h Φ xi , y h ( xi ) ; h mit y h ( x0 ) = ya
Die Funktion Φ(x,y;h) ist charakteristisch für das verwendete Einschrittverfahren
VORTEIL:
Die numerische Lösung im Intervall [a,b] erfolgt auf einem Gitter von Stützpunkten
xi, i=0,1, …, N mit x0=a, xN=b, welche bei einem Einschrittverfahren nicht
notwendigerweise äquidistant sein müssen. Die Schrittweite ist h bzw. hi=xi+1-xi
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
3
Probleme der Quantenmechanik
Probleme der Quantenmechanik erfordern die Lösung der Schrödingergleichung
Beispiel: Schrödingergleichung −  2 d 2 + V (x )ψ (x ) = Eψ (x )


2
m
dx
2
in einer Dimension


und Randbedingungen


2
d

2m
 2 + 2 (E − V (x ))ψ (x ) = 0



 dx 
w( x )


Gewöhnliche Differentialgleichung zweiter Ordnung
ψ ′′(x ) + w(x )ψ (x ) = 0
und Randbedingungen
Im Prinzip kann man diese Differentialgleichung durch ein Runge-Kutta-Verfahren
lösen. Meist verwendet man für die Lösung das Numerov Verfahren
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
4
Das Numerov Verfahren
Bekannt auch unter Fox-Goodwin-Verfahren
Man betrachtet die Differentialgleichung
Äquidistante Stützstellen:
0
u ′′ ( x ) + w ( x )u ( x ) =
x=
x min + j ∆ mit =
j 0,1,2,,N und u ( x j =
) uj
j
Darstellung der zweiten Ableitung mittels Taylorreihe:
1 2
1 3
1 4 (iv )
1 5 (v )
6
′
′′
′′′
±
∆
+
∆
±
∆
+
∆
±
∆
+
∆
u n ±=
u
u
u
u
u
u
O
(
)
n
n
n
n
n
n
1
2
6
24
120
Summation führt zu
=
u n′′
u n +1 − 2u n + u n −1
∆2
∆ 2 (iv )
− un + O ∆4
12
( )
Darstellung der vierten Ableitung mittels Differentialgleichung:
( iv )
un
w n +1u n +1 − 2w nu n + w n −1u n −1
2
′′
=
− (wu ) =
−
+
∆
O
∆2
138.074 Datenverarbeitung für TPH II
( )
Gewöhnliche Differentialgleichungen
5
Das Numerov Verfahren
Zusammenfassung aller Terme
u n +1 − 2u n + u n −1
u n′′ =
∆2
Zweischrittformel
w n +1u n +1 − 2w nu n + w n −1u n −1 
∆2 
4
−
−
+
∆
=
−w nu n
1
O
(
)


2
∆
12 

( )
 ∆2



 ∆2

∆2
1
w
u
2
10
w
u
1
w
0
+
−
−
+
+



n +1  n +1
n  n
n −1  u n −1 =
12
 12



 12

Algorithmus für praktische Rechnung
Qn +1 =
12u n − 10Qn − Qn −1
 ∆2

w
mit Qn =+
1

n u n
 12

Die Kenntnis der Lösung bei zwei Funktionswerten (Rand- oder Anfangsbedingung) ist für eine eindeutige Bestimmung von u erforderlich
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
6
Anwendung des Numerov-Verfahrens
Anfangs-/Randwertproblem:
u0=a, u1=b
 ∆2 
 ∆2 
Q0 = 1 + w0  u0 , Q1 = 1 + w1  u1
 12 
 12 
Q 2 = 12u1 − 10Q1 − Q0
u2 =
Q2
 ∆2 
1 + w2 
 12 
u0
u1
u2
Q3 = 12u2 − 10Q2 − Q1


Qn +1 = 12un − 10Qn − Qn −1
un +1 =
Qn +1

 ∆2
1 + wn +1 

 12
un+1

Hinweis: Für u“+wu =0 lässt sich in der RB un=0 oft die Linearität ausnützen.
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
7
Mehrschrittverfahren
Numerov Verfahren ist spezieller Algorithmus für gewöhnliche DifferentialGleichungen zweiter Ordnung  keine einfache Erweiterung von Einschritt V.
Nachstehend die Entwicklung von Algorithmen, die als Erweiterung von
Einschrittverfahren angesehen werden können.
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
8
Konstruktion von Mehrschrittverfahren
In einem Mehrschrittverfahren zur Lösung des Anfangswertproblems
y′ = f ( x, y ) mit y ( x0 ) = ya
Wird zu r >1 gegebenen Näherungswerten ηk für y(xk) k=j, j+1,…, j+r-1 ein neuer
Näherungswert für ηj+r für y(xj+r) berechnet.
y ′ = f ( x, y ) ⇒
x p+k
∫ dt f (t , y(t )) = y(x ) − y(x )
p+k
p− j
x p− j
Man ersetzt f(x,y) durch ein Polynom, welches an äquidistanten Stützstellen
xj=x0+jh die Funktion f(x,y) wiedergibt.
q
x p+k
i =0
x p− j
y (x p + k ) − y (x p − j ) = ∑ f (x p −i , y p −i ) ∫ dx Li (x ) mit Li (x ) =
q
(x − x )
∏ (x
 = 0 , ≠ i
p −
p −i
− x p − )
q
Mehrschrittverfahren
η p + k = η p − j + h∑ β qi f p −i
i =0
q
( + s ) für i = 0,1,2,..., q
1
β qi = ∫ dxLi (x ) = ∫ ds ∏
h x p− j
 = 0 , ≠ i ( − i )
−j
x p+k
138.074 Datenverarbeitung für TPH II
k
Gewöhnliche Differentialgleichungen
9
Prediktorverfahren
Verfahren von Adams-Bashforth:
k=1, j=0, q=0,1,2,…
η p +1 = η p + h[β q 0 f p + β q1 f p −1 +  β qq f p − q ]
1
β qi = ∫ ds
0
( + s )
∏
 = 0 , ≠ i ( − i )
q
für i = 0,1,2,..., q
βqi \ i
0
β0i
1
2β1i
3
-1
12β2i
23
-16
5
24β3i
55
-59
37
-9
720β4i
1901
-2774
2616
-1274
1
2
3
4
251
Verfahren von Nyström:
k=1, j=1, q=0,1,2,…
η p +1 = η p −1 + h[β q 0 f p + β q1 f p −1 +  β qq f p − q ]
1
β qi = ∫ ds
−1
( + s )
∏
 = 0 , ≠ i ( − i )
q
für i = 0,1,2,..., q
Beide Verfahren erlauben unabhängig
von der Funktion f(x,y) die explizite
Berechnung des nächsten Schritts
 Prediktorverfahren
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
10
Korrektorverfahren
Verfahren von Adams-Moulton:
k=0, j=1, q=0,1,2,…
η p = η p −1 + h[β q 0 f p + β q1 f p −1 +  β qq f p − q ]
0
β qi = ∫ ds
−1
( + s )
∏
 = 0 , ≠ i ( − i )
q
für i = 0,1,2,..., q
βqi \ i
0
β0i
1
2β1i
1
1
12β2i
5
8
-1
24β3i
9
19
-5
1
720β4i
251
646
-264
106
1
2
3
4
-19
Verfahren von Milne-Thompson:
k=0, j=2, q=0,1,2,…
η p = η p − 2 + h[β q 0 f p + β q1 f p −1 +  β qq f p − q ]
0
β qi = ∫ ds
−2
( + s )
∏
 = 0 , ≠ i ( − i )
q
für i = 0,1,2,..., q
Beide Verfahren erlauben für eine
allgemeine Funktion f(x,y) keine explizite
Berechnung des nächsten Schritts
 Korrektorverfahren
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
11
Allgemeine Mehrschrittverfahren
Allgemeine Form eines r-Schrittverfahren:
η j + r + ar −1η j + r −1 +  + a0η j = hF (x j ,η j + r ,η j + r −1 ,,η j ; h; f )
Bisher besprochen: Lineare Mehrschrittverfahren
F hängt linear von f ab
F (x j ;η j + r ,η j + r −1 ,  ,η j ; h; f ) =b r f (x j + r ,η j + r ) +  +b 0 f (x j ,η j )
Beispiel: r=q+1-Schrittverfahren von Adams-Bashforth
aq = −1, aq −1 =  = a0 = 0
bq +1 = 0
+s
bq −1 = β qi= ∫ ds ∏
 = 0 , ≠ i  − i
0
1
138.074 Datenverarbeitung für TPH II
q
Gewöhnliche Differentialgleichungen
12
Konsistenz von Mehrschrittverfahren
Analog zum Einschrittverfahren: Definition des lokalen Diskretisierungsfehlers
r −1
1


τ (x, y; h ) =  z (x + rh ) − hF ( x; z ( x + rh ), , z ( x ) ; h; f ) − ∑ ai z (x + ih ) 
h
i =0


Konsistenz eines Mehrschrittverfahrens
Mehrschrittverfahren konsistent, falls ∀ f ∈F 1 (a, b ) eine Funktion σ(h)
existiert mit lim σ (h ) = 0 , sodass
h →0
∀ x ∈ [a, b]
Verfahren p-ter Ordnung, falls für f ∈ Fp (a, b ) gilt σ (h ) = O(h p )
τ (x, y; h ) ≤ σ (h )
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
13
Konvergenz von Mehrschrittverfahren
Analog zum Einschrittverfahren: Definition des globalen Diskretisierungsfehlers
exakte Lösung
Fehler an den r Stützstellen

e( x, ε ; h ) = η ( x, ε ; h ) − y ( x )



ε i = ηi − y (xi )
Numerische Lösung
Konvergenz eines Mehrschrittverfahrens
Mehrschrittverfahren heißt konvergent, falls
limη ( x, ε ; hn ) = y ( x ),
n →∞
hn =
x − x0
mit n = 1, 2, 
n
Falls für alle x ∈ [a, b], f ∈ F1 (a, b ) und ∀ ε (z, h ) für welche ρ (h ) existiert,
die Beziehung gilt
ε (z , h ) ≤ ρ (h ) ∀ z ∈ Rh , lim ρ (h ) = 0.
h →0
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
14
Extrapolationsverfahren
Grundlage: asymptotische Entwicklung des globalen Diskretisierungsfehlers
Beispiel: Anfangswertproblem: y′ = f (x, y ) mit
Numerischer
Algorithmus
zur Integration
der Differentialgleichung
y ( x0 ) = y0 und x0 ∈ [a, b]
η (x0 ; h ) = y0
η (x0 + h; h ) = y0 + h f (x0 , y0 )

η (x + h; h ) = η (x − h; h ) + 2h f ( x,η (x; h ))

Der Algorithmus führt zu folgender Näherung η(x;h) der exakten Lösung y(x):
η (x; h ) = y (x ) + ∑ h 2 k [uk (x ) + (− 1x / h ) vk (x )]+ E2 N + 2 (x; h )
N
k =1
Fehler:
[
(
)
] ( )
e( x; h ) = η ( x; h ) − y ( x ) = h 2 u1 ( x ) + − 1x / h v1 ( x ) + O h 4
Oszillation mit n=x/h
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
15
Graggsche Funktion und Extrapolation
Graggsche Funktion:
Einsetzen des
Algorithmus
liefert
Entwickeln von
y ( x ± h ), uk ( x ± h ),
uk ( x ± h ) liefert
S ( x; h ) =
S ( x; h ) =
1
[η (x − h; h ) + 2η (x; h ) + η (x + h; h )]
4
N
1
2
{y(x ) + [ y(x + h ) + y(x − h )]}+ ∑ h 2 k {uk (x ) + 12 [uk (x + h ) + uk (x − h )]}
1
2
= (− 1)
x/h 1
2
1
2
k =1
∑ h {v (x ) − [v (x + h ) + v (x − h )]}+ O(h
N
2k
k
k =1
1
2
k
k
[
2 N +2
)
] (

1 d 2 y  N 2k ~
x/h ~
2 N +2
S ( x; h ) = y ( x ) + h u1 ( x ) +
 + ∑ h uk (x ) + (− 1) vk (x ) + O h
2
2 dx x  k = 2


2
Der führende Term der Entwicklung
enthält keinen oszillierenden Faktor
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
16
)
Graggscher Algorithmus: Anwendung
_
Gesucht: Lösung von y‘=f(x,y) an der Stelle x=x0+H
Algorithmus:
Rekursion für h = H
n
x1 = x0 + h

x j +1 = x j + h
η 0 = y0
η1 = y0 + hf (x,η 0 )

η j+1 =η j −1+2hf (x j ,η j ) für j = 1,2,, n − 1
Bildung der Graggschen Funktion: S ( x ; h ) = 12 [η n + η n −1 + hf (x = xn ,η n )]
Durchführung: _
Berechnen von S(x;hi) für eine Folge von Schrittweiten hi=H/ni mit ni=2,4,6,…
S ( x ; h ) = y ( x ) + a1h 2 +  + ak h 2 k
Anwendung des Neville Algorithmus für Extrapolation auf h=0 liefert
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
17
Vergleich der Algorithmen
Einschrittverfahren
Vorteil: optimierte variable Schrittweite
Nachteil: starre Ordnung, hoher Aufwand
Mehrschrittverfahren
Vorteil: bei linearen Problemen, geringerer Aufwand
Nachteil: starre Ordnung, feste Schrittweite, erste Schritte
mit Einschrittverfahren
Extrapolationsverfahren
Vorteil: keine feste Ordnung, hohe Genauigkeit mit geringem
Aufwand, einfach für komplexe Probleme
Nachteil: bei einfachen Problemen wirken sich Vorteile nicht aus
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
18
Computational Physics - Probleme der Quantenmechanik
Mikroskopische Systeme werden im Rahmen der Quantenmechanik
durch die Wellenfunktion beschrieben, welche sich als Lösung der
Schrödingergleichung unter vorgegebenen Anfangs- bzw. Randbedingungen ergibt. Zur numerischen Lösung versucht man die
Dimension des Problems durch geeignete Entwicklungen (z.B.
Partialwellenentwicklung) zu reduzieren.
Typische Fragestellungen der Quantenmechanik sind:
(1) Bindungszustände der radialen Schrödingergleichung
(2) Streulösung der radialen Schrödingergleichung
(3) Reflexion und Transmission am Potentialwall
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
19
Radiale Schrödingergleichung: Probleme
Viele Fragestellungen in quantenmechanischen Problemen erfordern die
2

 


2
Lösung der Schrödingergleichung.
(
)
(
)
(
)
ψ
ψ
V
r
r
E
r
−
∇
+
=


 2m


Für zentralsymmetrische Probleme V (r ) = V (r )
Partialwellenentwicklung
Radiale Schrödingergleichung
∞

u (r )
ψ (r ) = ∑  P (cos θ )
r
 =0
 2 d 2

(
)
−
+
V
r

 u (r ) = Eu (r )
2
 2m dr

Anwendungsbeispiele:
Berechnung von Bindungszuständen
Bindungszustände im H-Atom
Bindungszustände von Neutronen im Gravitationsfeld
Berechnung von Streuzuständen
Streuung von Neutronen an einem Kernpotential – Levinson-Theorem
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
20
Eigenschaften der radialen Schrödingergleichung
Die radiale Schrödingergleichung hat eine Singularität bei r=0
∞
Fuchssche Klasse: für r  0 gilt u (r ) = ∑ an r α + n = a0 r α + a1r α + a2 r α + 2 + 
n =0
Einsetzen des verallgemeinerten Potenzreihenansatz führt auf
∞
2m

α + n−2
α + n−2
α +n 
(
)(
)
(
)
(
(
)
)
+
+
−
1
−
+
1
+
−
α
n
α
n
a
r
a
r
E
V
r
a
r



=0
∑
n
n
n
2


n =0 
Koeffizientenvergleich für n=0 führt auf Bestimmungsgleichung für α
α (α − 1) − ( + 1) = 0 ⇒ α = 12 ± ( + 12 )
Differentialgleichung mit
Singularität bei r=0
a0 r  +1
reguläre Lösung
u (r ) r
→ −
→0
irreguläre Lösungen
 a0 r
Anfangswertproblem für regulären Lösung: u (r = 0) = 0, u (r = ∆r ) = g ≠ 0
Anfangswertproblem für irreguläre Lösung: u (r = R1 ) = g1 , u (r = R2 ) = g 2
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
∆r > 0
∆r < 0
21
Anwendung des Numerov Verfahrens
u ′′(x ) + w(x )u (x ) = 0
2m
( + 1)
x → r , u (x ) → u (r ) und w (x ) → w(r ) = 2 (E − V (r )) −
r2

Man betrachtet die Differentialgleichung
x min + j ∆ mit =
j 0,1,2,,N und u ( x j =
Äquidistante Stützstellen: x =
) uj
j
Zweischrittformel
 ∆2



 ∆2

∆2
1
w
u
2
10
w
u
1
w
0
+
−
−
+
+



n +1  n +1
n  n
n −1  u n −1 =
12
 12



 12

Algorithmus für praktische Rechnung
Qn +1 =
12u n − 10Qn − Qn −1
 ∆2

mit Qn =+
w n u n
1
 12

Die Kenntnis der Lösung bei zwei Funktionswerten (Rand- oder Anfangsbedingung) ist für eine eindeutige Bestimmung von u erforderlich
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
22
Spezialfall: reguläre Lösung für p-Wellen
Bei einer regulären Lösung ist u0=0. Damit wird in den meisten Fällen Q0=0.
Aufgrund der Singularität im Zentrifugalwall der radialen Schrödingergleichung kann es aber zu endlichen Werten kommen.
( + 1) 
 2m
 +1
 +1
 −1
(
(
)
)
(
)
=
−
+

→
⇒
=
−
=
−


0
1
u (r ) r
a
r
w
u
E
V
r
a
r
a
r


0
0 0
0
0
2
→0
r2 

0
für  = 0,2,3, 

 2
⇒ Q0 =  ∆
1
2
(
)
(
)
−
=
−
=
∆
=
=
∆
=
∆

a
u
r
u
r
2
für
1
mit
a
0
0
 12
6
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
23
Bindungszustände der radialen Schrödingergleichung
Beispiel H-Atom
  2  d 2  (  + 1) 

Wellenfunktion u ( r )
E u (r )
−
 2−
 + V ( r )  u (r ) =
2
r
 2m  dr

Energie E

Umformung


2
 (  + 1)
2me
d

2
2
+
+
−
=
=
k
U
r
u
r
k
E
(
)
(
)
0
mit
 dr 2

2
2

r



w( r )


Beispiel: H-Atom
Coulombpotential
r
V (r ) = −
Elektron
138.074 Datenverarbeitung für TPH II
Zα f c
r
Z
Ordnungszahl, Zahl der Protonen
α f = 1./137.035989
Feinstrukturzahl
c=197.327053 eVnm
me c 2 = 0.51099906 MeV Ruhemasse des Elektrons
Gewöhnliche Differentialgleichungen
24
Problemangepasste Einheiten
Die numerische Lösung physikalischer Probleme sollte mit angepassten
Einheiten erfolgen.
=
ρ
r
c
a0 =
=
mit Bohrradius
0, 05291772 nm
2
a0
α f me c
Transformation der Differentialgleichung führt auf


 d2
 (  + 1) 2 Z 
 2 +ε −
 u ( ρ ) =
+
0
2
ρ
ρ 
 d ρ 


w ( ρ )
Dimensionslose Form
der Differentialgleichung
Die Energie ist in Einheiten der Bohrenergie E0 gegeben
=
ε
E
E0
mit E0
=
1
me c 2α 2f 13.59829 eV
=
2
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
25
Berechnung von Bindungszuständen
Eine charakteristische Eigenschaft
von Bindungszuständen ist, dass sie
∞
2
quadrat-integrabel sind, d.h.
dρ u~ (ρ ; ε ) = C mit 0 ≤ C < ∞
∫
0
Bedingung an Bindungswellenfunktion im Asymptotischen:
Damit dieses Integral endlich bleibt, muss die Lösung für asymptotische r Werte verschwinden, d.h.wir suchen Lösungen mit der Eigenschaft
(
u~ (ρ ) ρ
→ C exp − − ε ρ
→∞
)
mit ε < 0
Bedingung an Bindungswellenfunktion im Ursprung:
Der Bindungszustand muss aber gleichzeitig auch eine reguläre Lösung
sein, d.h. der Wert von u~ (ρ ; ε ) muss am Ursprung verschwinden.
Beide Bedingungen können gleichzeitig nur für diskrete ε-Werte erfüllt
werden, welche numerisch durch mehrmalige gezielte Versuche (EinfachSchießverfahren) iterativ bestimmt werden.
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
26
Radiale Schrödingergleichung – Beispiel H-Atom
  2  d 2  (  + 1) 

Wellenfunktion u ( r )
E u (r )
−
 2−
 + V ( r )  u (r ) =
2
r
 2m  dr

Energie E

Umformung


2
 (  + 1)
2me
d

2
2
+
+
−
=
=
k
U
r
u
r
k
E
(
)
(
)
0
mit
 dr 2

2
2

r



w( r )


Beispiel: H-Atom
Coulombpotential
r
V (r ) = −
Elektron
138.074 Datenverarbeitung für TPH II
Zα f c
r
Z
Ordnungszahl, Zahl der Protonen
α f = 1./137.035989
Feinstrukturzahl
c=197.327053 eVnm
me c 2 = 0.51099906 MeV Ruhemasse des Elektrons
Gewöhnliche Differentialgleichungen
27
Eigenschaften der radialen
Schrödingergleichung - Reguläre Lösung
In physikalischen Problemen sind wir meist an regulären Lösungen interessiert,
d.s. Lösungen mit endlicher Wahrscheinlichkeitsdichte bei r = 0.


 d2
 (  + 1) 2 Z 
 2 +ε −
 u ( ρ ) =
+
0
2
ρ
ρ 
 d ρ 


w ( ρ )
c 0 ρ  +1 reguläre Lösung
Differentialgleichung mit
⇒ u ( ρ ) 
→
ρ →0
−
Singularität bei r=0
d
ρ
irreguläre Lösung
 0
Für die numerische Bestimmung der regulären Lösung muss man
folgende Startwerte für den Numerov Algorithmus festlegen:
u0= 0 und u=
g ≠0
1
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
28
Das Einfach-Schießverfahren
Bindungszustände sind durch diskrete Energieigenwerte charakterisiert, welche man
iterativ bestimmen muss.
Start der Nullstellenbestimmung: Wahl von ε < 0 und Berechnung von
(
u ( ρN=
exp − −ε ρN
) u=
N
(
)
)
(
uN=
und u ( ρN −=
exp − −ε ρN −1
1)
−1
(
)
)
bzw. um = n  i −ε ρm − i j  i −ε ρm  mit m = N ,N − 1


Lösen der Differentialgleichung: von außen nach innen, d.h.
D0
QN −2 ,uN −2 ,QN −3 ,uN −3 ,,Q1,u1,Q 0
Berechnung von D0:
D=
Q0 (ε ,  ) +
0 (ε ,  )
u1
6
δ 1
Bestimmung der Nullstelle von D0: Die Nullstelle
D0 bestimmt die Energie des Bindungszustands
138.074 Datenverarbeitung für TPH II
0 ε
ε Bindungszustand
Gewöhnliche Differentialgleichungen
29
Streulösungen und die Bestimmung der Streuphasen
Die asymptotische Form der radialen Wellenfunktion für Streulösungen ist bei
vorgegebener Bahndrehimpulsquantenzahl und potentialen endlicher Reichweite
u (r , k )
= A[cos(δ ) ˆj (kr ) − sin (δ )nˆ (kr )] =
r →∞



Streuphase
sphärische Besselfunktion
π

Riccati-Form ˆj (kr ) = kr j (kr ) = sin kr −  
r →∞

2

r →∞
A sin (kr + δ  )
sphärische Besselfunktion
π

Riccati-Form nˆ (kr ) = kr n (kr ) = − cos kr −  
r →∞

2
Man integriert numerisch die Wellenfunktion r=0 ausgehend über h,2h,… bis r1
bzw. r2 und erhält numerisch die Werte u1=u(r1,k) bzw. u2=u(r2,k). Die Streuphase
erhält man durch Vergleich mit der asymptotischen Form von u(r,k):
ˆj (kr1 ) − tan (δ  )nˆ (kr1 )
u1 ˆj (kr2 ) − u2 ˆj (kr1 )
u1
=
⇒ tan (δ  ) =
u2 ˆj (kr2 ) − tan (δ  )nˆ (kr2 )
u1nˆ (kr2 ) − u2 nˆ (kr1 )
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
30
Beispiel: Levinson Theorem
Levinson Theorem:
Für eine gegebene Partialwelle nimmt die absolute Streuphase δ(E) bei der
Energie E=0 hat den Wert δ(0)=nπ an, wobei n die Anzahl der Bindungszustände des Potentials in der Partialwelle ist. Bei Existenz eines halbgebundenen Zustands (Bindungszustand bei E=0) nimmt die Streuphase den
Wert δ(0)=(n+0.5)π an.
Die numerische Rechnung bestimmt die Streuphase δ modulo π.
Unter der absoluten Streuphase versteht man die stetige Kurve δ(E) zwischen
E=0 und E unendlich, δ
Resonanzen
nπ
wobei δ  0 für
absolute
Streuphase
E unendlich
Numerisch bestimmte
Streuphase
π
138.074 Datenverarbeitung für TPH II
E
Gewöhnliche Differentialgleichungen
31
Quantenmechanik in einer Dimension
Wir betrachten ein Teilchen der Masse m, welches sich in einem
Potential V(x) bewegt
 2 ∂ 2

∂
+ V ( x ) ψ ( x, t ) = i ψ ( x, t )

2
∂t
2m ∂x



Hamilton Operator
explizit zeitunabhängig
Energie E ist eine
Erhaltungsgröße
Betrachtung stationärer Zustände
ψ ( x, t ) = u ( x ) e
E
−i t

 d2

2mE
2m
2
2
=
u ( x ) 0 mit
k
, =
U ( x)
V ( x)
 2 + k − U ( x ) =
2
2


 dx

138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
32
Das eindimensionale Streuproblem
 2

 d + k 2 − U ( x )  Ψ (k , x) =
0
2
 dx  
w( x )


Allgemeine Lösung für U=0
Ψ=
A exp ( ikx ) + B exp ( −ikx )
0 ( x)
V
R(k) e-ikx
T(k)eikx
eikx
0
I
a
II
x
III
Ψ und Ψ‘ sind stetig
Ψ I (=
x) exp ( ikx ) + R(k ) exp ( −ikx )
138.074 Datenverarbeitung für TPH II
Ψ III ( x) =
T ( k ) exp ( ikx )
Gewöhnliche Differentialgleichungen
33
Berechnung von R(k) und T(k)
Um R(k) und T(k) für einen Strahl einfallend von links numerisch zu bestimmen,
müssen folgende Schritte durchgeführt werden.
1.
Man startet im Bereich III (x>a), in welchem man u(x) bis auf eine
u ( x ) = eikx
Konstante kennt, setzt man an:
2.
Man löst die Schrödingergleichung numerisch von x > a bis x < 0 mit
dem Ansatz von 1.
3.
Im Bereich I (x<0) hat die Lösung die analytische Form
u ( x )
=
1 ikx R ( k ) − ikx
e +
e
T (k )
T (k )


α (k )
β (k )
Durch Vergleich der numerischen mit der analytischen Form lassen
sich R(k) und T(k) bestimmen.
138.074 Datenverarbeitung für TPH II
Gewöhnliche Differentialgleichungen
34
Berechnung von R(k) und T(k)
Man drückt die numerische Lösung an zwei Stützstellen x1, x2 < 0 durch die
analytische Form aus,
u ( x1=
) u=1
1 ikx1 R ( k ) − ikx1
e +
e
T (k )
T (k )
u ( x2=
) u=2
1 ikx2 R ( k ) − ikx2
e +
e
T (k )
T (k )
Aus diesem Gleichungssystem kann
man den Reflexions- und den
Transmissionkoeffizienten
berechnen.
eikx1 u2 − eikx2 u1
R ( k ) = − − ikx1
e u2 − e − ikx2 u1
1 ikx1
e + R ( k ) e − ikx1 
=
T (k )
u1
r (q) = R (k )
138.074 Datenverarbeitung für TPH II
2
Reflektivität
Gewöhnliche Differentialgleichungen
35
Praktische Anwendung: Neutronenreflektometrie
Aufbau eines Reflektometers
(Röntgenstrahlung, Neutronen)
Einfallender
Strahl
Reflektierter
Strahl
e
ikx
R(k ) e − ikx
0
V(x)
a
Transmittierter
Strahl
138.074 Datenverarbeitung für TPH II
x
Gewöhnliche Differentialgleichungen
T (k ) eikx
36