Kettengetriebe

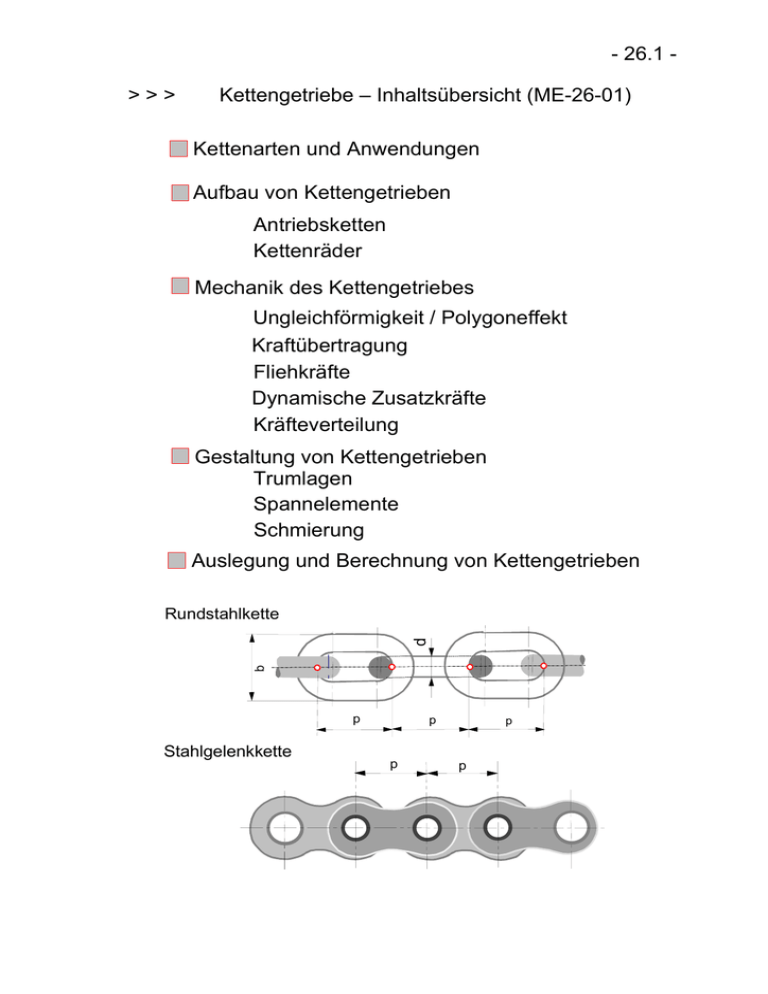
- 26.1 >>>
Kettengetriebe – Inhaltsübersicht (ME-26-01)
Kettenarten und Anwendungen
Aufbau von Kettengetrieben
Antriebsketten
Kettenräder
Mechanik des Kettengetriebes
Ungleichförmigkeit / Polygoneffekt
Kraftübertragung
Fliehkräfte
Dynamische Zusatzkräfte
Kräfteverteilung
Gestaltung von Kettengetrieben
Trumlagen
Spannelemente
Schmierung
Auslegung und Berechnung von Kettengetrieben
b
d
Rundstahlkette
p
Stahlgelenkkette
p
p
p
p
- 26.2 -
Kettengetriebe - Allgemeines
>>>
Kettengetriebe – Merkmale (ME-26-02)
Anwendungen:
Übertragung großer Kräfte bei geringen Geschwindigkeiten (Hubschlitten am Gabelstapler,
Schiffshebewerke)
Tragen großer Lasten mit Lastketten
Leistungsübertragung bei Geschwindigkeiten bis
1 m/s mit Förderketten (Rolltreppen, Transferförderer)
Übertragung hoher Leistungen
Kettengetriebe mit Antriebsketten
- 26.3 -
Kettenarten und Anwendungen
Arten:
Lastketten
Förderketten
Antriebsketten
Bauformen:
i Rundstahlketten
i Stahlgelenkketten
i Spezialketten in der Fördertechnik, wie Kreuzgelenkkette, Steckkette und Gliederbandkette
i Fahrwerksraupen
i Antriebsketten: Rollen- u. Hülsenketten
Anwendungen:
∆
Lastanschlagketten
∆
Ankerketten
∆
Kettenhubgeräte
∆
Kreiskettenförderer (v < 1 m/s)
- 26.4 -
Stahlgelenkketten
Definition:
Gelenkketten sind solche Ketten, die in jeder Teilung ein
Gelenk besitzen. Stahlgelenkketten sind Gelenkketten aus
Stahl.
Bauformen:
i
i
i
i
i
i
i
i
>>>
Gallkette
Flyerkette
Blockkette
Ziehbankkette
Buchsenkette
Hülsenkette
Rollenkette
Zahnketten
Stahlgelenkketten (Beispiele) (ME-26-04)
Gallkette:
Gallkette (Erfinder französischer Ingenieur)
Als Antriebskette entwickelt, hierfür heute nicht
mehr verwendet
>
Lastkette (hohe Bruchlast)
>
Förderkette
- 26.5 Spezialketten in der Fördertechnik (ME-26-05)
Flyer-Kette
Aufbau:
Bolzen-Laschenpakete (Schnittigkeit)
Eigenschaften:
>
>
>
>
Sehr hohe Bruchlast
geringe Geschwindigkeit
kein Zahneingriff möglich
kleiner Umlenkradius
Anwendung
Reine Lastkette, z. B.: Hubschlitten am Gabelstapler
Rotary-Kette
Bei der Rotary-Kette sind alle Laschen gekröpft.
Vorteile:
-
Gliederzahl der geschlossenen Kette beliebig (gerade und ungerade).
Die Kette ist elastisch und stoßdämpfend.
Anwendung:
-
Tiefbohranlagen nach dem Rotary-System
Raupenantriebe von Baumaschinen.
- 26.6 Spezialketten in der Fördertechnik (ME-26-05)
Gabelkette
Aufbau:
Je Glied ein Gabelkopf mit Bolzengelenk und ein einfaches
Gliedende.
Eigenschaften/Anwendungen:
Sehr robust und unempfindlich gegen abrasiven Schmutz.
In zweisträngiger Form mit Stegen stellt sie die Grundform
des Trogketten oder Kratzerförderer dar.
Kreuzgelenkkette
Aufbau:
Jedes Teil besitzt ein Kreuzgelenk, das Schwenk- (Knick-)
Bewegungen in zwei ineinander senkrechten Ebenen ermöglicht.
Anwendungen:
Räumliche Transferfördereinrichtungen
- 26.7 -
Aufbau von Kettengetrieben (ME-26-07)
Zweiwellengetriebe
Im einfachsten Fall besteht ein Kettengetriebe (Beispiel
Fahrrad) aus 2 parallelen Wellen im Abstand a mit Antriebskettenrad und Kette. Es können ein- und mehrsträngige Ketten auch in paralleler Anordung (bis zu 6 Strängen)
eingesetzt werden.
>>>
Aufbau von Kettengetrieben – Zweiwellengetriebe
(ME-26-07)
Bei stoßfreiem Betrieb wird ein ruhiger Lauf erreicht, wenn
der Neigungswinkel der Zentralen etwa 30° beträgt und das
Lasttrum oben liegt. Bei einem relativen Kettendurchhang
von
f/a = 0,01 .... 0,03
reicht die Stützkraft aus dem Eigengewicht der Kette für ein
ordnungsgemäßes Eingreifen der Kettenräder. Ansonsten
sind Führungs- und Spanneinrichtungen notwendig. Nachspannmöglichkeiten für die Längung infolge Verschleiß in
den Gelenken sind allemal erforderlich.
Die Anordnung erfolgt im Leertrum, möglichst von außen
nach innen durch eine Feder mit flacher Kennlinie oder hydraulisch belastet. Das von außen angesetzte Spannrad wird
im Abstand von 1/3 der Trumlänge vom Antriebsrad angesetzt. Bei der Anordnung von innen nach außen wird das
Spannrad etwa in der Mitte angesetzt. Der Spannweg ist so
zu bemessen, daß 3 % Kettenlängung kompensiert werden
können.
- 26.8 >>>
Nockenwellenantrieb eines Verbrennungsmotors
(ME-26-08)
Anwendungsbeispiel
BMW VANOS
- 26.9 -
Mehrwellengetriebe
Der Umschlingungswinkel von 120° reicht aus, um die
Nutzkraft zwischen Rad und Kette zu übertragen (etwa 10
bis maximal 14 Zähne im Eingriff). Daher eignen sich Kettengetriebe ganz besonders gut zur Gestaltung von Mehrwellengetrieben. Bei Umlenk- und Spannrädern genügen 3
Zähne im Eingriff.
>>>
Aufbau von Kettengetrieben (ME-26-09)
- Mehrwellengetriebe -
Bei Längenzunahme der Kette infolge von Gelenkverschleiß wird durch Spanneinrichtungen, die ständig mit einer Vorspannkraft auf die Kette wirken, ausgeglichen. Mit
Spanneinrichtungen können Trumschwingungen und damit
einhergehende Störeingriffe verhindert werden.
Die Zähnezahlen für Spannräder richten sich nach der Kettengeschwindigkeit:
Zs < 9 für handbetriebene Einrichtungen
Zs = 9 ... 13 für v ≤ 4 m/s
Zs = 14 - 16 für 4 m/s ≤ ∨ ≤ 7 m/s
Zs = 17 für ∨ > 7 m/s
Je größer die Zähnezahl des Spannrades ist, desto ruhiger
wird der Lauf der Kette. Häufig wird Zs = Z1 gewählt. Zur
Vermeidung/Verminderung von Kettenschwingungen werden Leiträder, Führungsschienen beim Nockenwellenantrieb, Stützräder in Obertrum oder auch Stützschienen bei
Kettenfahrzeugen eingesetzt. Grundsätzlich sollen Ketten
gut geschmiert sein, wozu Schmiereinrichtungen eingesetzt
werden.
- 26.10 -
Antriebsketten
Definition:
Antriebsketten sind Zugmittel, mit denen Bewegungen und
Kräfte zwischen Kettenrädern übertragen werden.
>>>
Antriebsketten I – Bauformen (ME-25-10)
Aufbau:
Innenglied / Außenglied
Ein- oder mehrsträngig
Innenglied:
2 Laschen mit eingenieteten Buchsen
Außenglied:
Lasche mit eingenieteten Bolzen und Verschlußlasche
In Verbindung mit dickwandigen Rollen ergibt sich die Rollenkette.
Die Gleitbewegung der Buchse beim Einlauf in das Kettenrad wird in eine Drehbewegung umgesetzt.
-
Verschleiß wird geringer
höhere zulässige Kettengeschwindigkeit
Hülsenketten:
v
≤ 12 m/s
Rollenketten:
v bis 35 m/s, bei besonderen Maßnahmen
- 26.11 >>>
Antriebsketten II – Gelenkverschleiß (ME-26-11)
26-11
Folie ME-26-11.dsf
- 26.12 >>>
Antriebsketten III (ME-26-12)
-
Kettenkonstruktionen für höhere Geschwindigkeiten und Leistungen -
Verminderung der Kettenmasse
Rollenkette mit Hohlbolzen
Verminderung der Gelenkreibung
Rollenkette mit Kunststoffhülse
außerdem z. B. durch Zahnketten mit Wälzgelenk
Verminderung der Teilung und Erhöhung der
Belastbarkeit durch Mehrstrangketten (bis zu 6 Stränge)
Zweifachrollenketten
mit Hohlbolzen
Dreifachrollenketten
- 26.13 Verschlußglieder
>>>
Antriebsketten IV (ME-26-13)
- Verschlußglieder -
Verschlußglieder sind für alle Kettenkonstruktionen erhältlich:
-
Einfache Verschlußglieder für gerade Gliedzahlen
der geschlossenen Kette
-
gekröpfte Doppelglieder für ungerade Gliedzahlen.
Hinweis:
Gerade Gliedzahlen bevorzugen !
(Biegespannung im gekröpften Doppelglied; allerdings treten Laschenbrüche selten auf.)
- 26.14 >>>
Antriebsketten für höhere Geschwindigkeiten
- Ablegereife – (ME-26-14)
Antriebsketten
- Ablegereife Die Kette ist, wie auch alle anderen Zugmittel, ein Verschleißteil
mit begrenzter Lebensdauer. Unter günstigen Betriebsbedingungen wird eine Volllastlebensdauer von 15 000 Betriebsstunden
erreicht. Hauptsächlich tritt Verschleiß an den Gelenken auf, wodurch Teilung und Kettenlänge zunehmen. Deswegen steigt die
Kette auf.
Aufsteigen der Kette
Mit zunehmender Längung der Kette wächst die Gefahr des Überspringens. Die Teilungsfehler addieren sich bei sehr großen Zähnezahlen. Deswegen wird die Zähnezahl bei Großrädern beschränkt.
max z2 = 120
Wegen der Mindestzähnezahl beim Ritzel und der maximalen Zähnezahl beim Rad ist das Übersetzungsverhältnis bei Leistungsgetrieben
beschränkt:
i = z2 / z1 <
- 7
Ablegereife der Kette
Die Ablegereife der Kette ist erreicht, wenn die relative Kettenlängung
∆ l / l = 0,03
beträgt. Bei hohen Anforderungen werden die Ketten bereits bei relativen Kettenlängungen von 1% erneuert.
- 26.15 >>>
Kettenräder (ME-26-15)
Kettenräder
p
d0 =
p. z
p
=
sin ( 180°/ z )
π
k
rk
Kettenräder für
Rollenkettengetriebe
1
da = Kopfkreis- /
p = Teilung
d 0 = Teilkreis- /
γ
do
du
rc
hm
f
φ
Hi
lfs
d
da
γ
es
se
r
γ
= 1/2 Teilungswinkel
= Flankenwinkel
r1 = Radius- Fußausrundung
rK = Zahnkopfradius
ds
k = Kopfhöhe
B3
bz
e
zweifach
ds
einfach
ds
e
bz
bz
bz
bz
bz
e
dreifach
ds
B2
B1
Werkstoffe: GG: St 60; St 70; St gehärtet
Zähnezahlen :
Primzahlen bevorzugen !
Für geringe Ansprüche an die Laufruhe z 1-< 17;
für Leistungsgetriebe und höhere Ansprüche z1 =19...25...(30)
Wegen geringer Geschwindigkeiten werden in der Fördertechnik größere
Ungleichförmigkeiten in Kauf genommen: Polygonrad eines Plattenbandförderers mit z= 6; Kettennuss eines Kettenhebezeuges mit z=5.
p
- 26.16 Mechanik des Kettentriebes
Bei konstanter Umlaufgeschwindigkeit des treibenden Kettenrades wird die Trumgeschwindigkeit ungleichmäßig
Polygoneffekt.
>>>
Mechanik des Kettentriebes I (ME-26-16)
Das Trum wird von demjenigen Gelenk der Kette geführt,
das als letztes in den Eingriff mit dem Kettenrad gelangt ist:
-
Das Trum wird gehoben und gesenkt.
>
Transversalschwingungen
-
Das Trum wird in Längsrichtung ungleichförmig
bewegt.
>
Longitudinalschwingungen
-
Die Vorgänge wiederholen sich mit der Zahneingriffsfrequenz.
- 26.17 Geschwindigkeitsbetrachtung
Die Umfangsgeschwindigkeit des Trumführungspunktes ist
konstant:
v u = r0 ⋅ ω = const
Die Tangentialkomponente, die der Längsgeschwindigkeit
(vl) des Trums entspricht, ergibt sich aus dem aktuellen
Stellungswinkel α des Trumführungspunktes:
v l = vu ⋅ cos α
Der Maximalwert der tangentialen Trumgeschwindigkeit (vl)
liegt vor, wenn α = 0 ist, also:
v l max = v u = r0 ⋅ ω
Die Radialkomponente (vq) der Trumgeschwindigkeit hängt
ebenfalls vom aktuellen Stellungswinkel des Trumführungspunktes ab:
v q = v u ⋅ sin α ;
Maximalwert bei
α = −φ
Null bei
α=0
Minimalwert bei
α = + φ( v r < 0 )
- 26.18 -
Umgleichförmigkeit der Kraft- und Bewegungsübertragung
>>>
Mechanik des Kettentriebes II (ME-26-18)
Die Geschwindigkeitsänderungen in tangentialer und radialer Richtung verlaufen periodisch.
Periodenwinkel:
α = − φ bis α = + φ
Der Periodenwinkel ist der Zentriwinkel des treibenden Kettenrades zwischen zwei aufeinanderfolgenden Zähnen, also
2 φ.
Im weiteren wird nur noch die Trumgeschwindigkeit in
Längsrichtung betrachtet.
- 26.19 Auswirkung der Ungleichförmigkeit im Lasttrum auf die
Drehbewegung der Welle 2
Bei einem Kettentrieb mit i = 1, also z1 = z2 und gerader
ganzzahliger Gliedzahl im ziehenden Trum ist die Drehbewegung der Welle 2 genauso gleichförmig wie die der Welle
1:
δ=0
Die Ungleichförmigkeit im Trum hebt sich am Rad 2 auf.
Ist die Gliederzahl im Lasttrum ungerade, so nimmt die Ungleichförmigkeit zu:
>>>
Mechanik des Kettentriebes III (ME-26-19)
- Ungleichförmigkeitsgrad -
Mit zunehmender Zähnezahl z1 wird die Ungleichförmigkeit
der Welle 2 erheblich besser.
- 26.20 Die Ableitung der Trumgeschwindigkeit nach der Zeit ergibt
die Kettenbeschleunigung.
al =
dv l
in Trumlängsrichtung
dt
> > > Mechanik des Kettentriebes IV (ME-26-20)
- Kettenbeschleunigung -
Die maximale Beschleunigung ergibt sich zu:
max al = p ⋅ ω2
2
Diese hängt ab von:
Maßnahmen zur Erzielung geringer Kettenbeschleunigung.
d0 groß, damit ω klein wird.
z groß, damit p klein wird.
Die Beschleunigungen führen zu Trägheitskräften. Diese
Kräfte sind wegen der Längselastizität der Kette und dem
Schmierstoff in den Gelenken tatsächlich geringer als die
rechnerischen Werte. Sie führen aber zur Erregung von
Kettenschwingungen. Die Erregerfrequenz ist die Zahneingriffsfrequenz.
- 26.21 -
Fliehkraft
Die Fliehkraft ist Zugkraft, die sich über der gesamten Kettenlänge auswirkt. Sie entsteht infolge des Umlaufs der Kette an den Kettenrädern.
> > > Herleitung der Fliehkraft (ME-26-21)
Die Fliehkraft ist eine Blindkraft, die mit v2 ansteigt. Die
Fliehkraft belastet die Kette insbesondere die Kettenglenke,
wodurch die optimale Kettengeschwindigkeit gering wird.
vopt = 5 ... 8 ... 10 m/s je nach Kettenkonstruktion.
- 26.22 -
Kräfte am Kettenrad
Umfangskraft über den Drehwinkel (ME-26-22)
Bei konstantem Drehmoment ändert sich die Umfangskraft
mit der wirksamen Hebellänge r am Kettenrad:
rmin ≤ r ≤ rmax = r0
Die Umfangskraft schwingt periodisch zwischen Fu,max und
Fu,min
Der Mittelwert der Umfangskraft Fu ergibt ein flächengleiches Rechteck über dem Periodenwinkel 2 ϕ :
)
+ϕ
1
) )
⋅ ∫) Fu (α )dα
Fu =
2 ⋅ ϕ −ϕ
Bei praktischen Berechnungen genügt der Nennwert:
Fu ≈
2 ⋅ Md
d0
mit einem Fehler < 1,4 % bei z1 = 19.
- 26.23 -
Kraftübertragung zwischen Kette und Kettenrad
Die nachfolgende Herleitung berücksichtigt nicht etwaige
Fliehkräfte, ferner wird Kraft im ziehenden Trum gleich der
Nutzkraft gesetzt F1 ≈ Fu .
> > > Kraftübertragung zwischen Kettenrad und Kette (Rollenkette) (ME-26-23)
Betrachtet wird zunächst das erste Kettenglied im Zahneingriff am Lasttrum.
Die Änderung der Zugkraft, zwischen beiden Gelenken ergibt sich
für Gleichgewicht:
r ausrdem Kräfteplan
r
Fu1 = FN1 + Fu2
Nach dem Sinussatz ergibt sich:
Fu2 = Fu1 ⋅
sin(ϕ + γ − α )
sin(2ϕ + γ )
An allen davorliegenden Gelenken spielt der Winkel α keine
Rolle mehr:
sin γ
Fu,i+1 = Fu,i ⋅
sin(2ϕ + γ )
1424
3
const
Ergebnis:
Die Zugkräfte in den einzelnen Gliedern werden nach einer
geometrischen Reihe von Zahn zu Zahn abgebaut (5 Eingriffszähne genügen!). Über dem Umfang des Rades in radialer Richtung dargestellt, ergibt sich eine Spirale (ähnlich
dem Trumkraftabbau auf dem Wirkbogen einer Treibriemenscheibe).
- 26.24 -
Trumkraftverteilung beim Kettenantrieb
> > > Kräfte am Kettentrieb (ME-26-24)
Vorstellung:
Hinterradantrieb am Fahrrad
Nutzkraft:
Bewegungswiderstände des Fahrrades:
-
Rollwiderstand
-
Steigungswiderstand
-
Beschleunigungswiderstand
Kräfte im Leertrum, F2:
-
Stützkraft
-
Fliehkraft
Kräfte im Lasttrum, F1:
-
Kraft im Leertrum
+ - Umfangskraft
+
Vorspannkraft
+ - dynamische Zusatzkräfte
∑ = Fres , schwellend
}
∑ Fw = Fu