Messung des Konzentrationsfeldes verdunstender binärer

Messung des Konzentrationsfeldes
verdunstender binärer Mikropartikel
mittels linearer Raman-Spektroskopie
Dissertation
zur
Erlangung des Grades
Doktor-Ingenieur
der
Fakultät für Maschinenbau
der Ruhr-Universität Bochum
von
Helge Moritz
aus Braunschweig
Bochum 1999
Dissertation eingereicht am:
17. November 1998
Tag der mündlichen Prüfung:
08. Februar 1999
Erster Referent:
Prof. Dr. techn. Gustav Schweiger
Zweiter Referent:
Prof. Dr.-Ing. Cameron Tropea
III
Vorwort
Diese Dissertation entstand während meiner wissenschaftlichen Tätigkeit an der
Ruhr-Universität Bochum am Lehrstuhl für Laseranwendungstechnik und Meßsysteme
im Rahmen des Teilprojektes A1 „Raman-Spektroskopie an Aerosolen“ im Sonderforschungsbereich 209 „Stoff- und Energietransport in Aerosolen“ sowie des
Forschungsprojektes „Entwicklung und Erprobung eines optischen Meßverfahrens zur
Untersuchung transienter Reaktionen und Transportprozesse in Mehrphasensystemen“
(DFG Schw 184/19-1). Der Deutschen Forschungsgemeinschaft möchte ich für die
großzügige finanzielle Unterstützung dieser Projekte danken.
Das erfolgreiche Gelingen dieser Arbeit wurde durch die hilfreiche Unterstützung
einiger Personen begünstigt. Ich möchte mich daher bei all denjenigen bedanken, die zu
dieser Arbeit beigetragen haben.
An erster Stelle gilt mein Dank Herrn Prof. Dr. techn. Gustav Schweiger für die
Aufnahme in seine Arbeitsgruppe sowie besonders für die Unterstützung und Anleitung
zu dieser Arbeit.
Herrn Prof. Dr.-Ing. Cameron Tropea (Fachgebiet Strömungslehre und Aerodynamik,
Technische Universität Darmstadt) danke ich für die freundliche Übernahme des
Korreferates.
Ferner möchte ich allen Kollegen des Lehrstuhls für Laseranwendungstechnik und
Meßsysteme für die freundliche Zusammenarbeit und ihre Hilfsbereitschaft danken.
Dabei möchte ich besonders die Zusammenarbeit mit Dr. Thomas Kaiser und Dr. Stefan
Lange hervorheben, die einen entscheidenden Anteil an der Evaluation der
experimentellen Ergebnisse meiner Dissertation haben. Von Herrn Dr. Reinhard Vehring
VORWORT
IV
übernahm ich die Bearbeitung des Teilprojektes A1 im SFB 209. Für die Einweisung in
den Versuchsstand möchte ich mich bei ihm bedanken. Außerdem danke ich Dorothee
Lemken und Andreas Hangkamer-Kühnen, die als studentische Mitarbeiter für mich
tätig waren.
Zu guter Letzt möchte ich mich auch bei meiner Frau Claudia und meinen Kindern
Anika, Meike und Björn für ihr Verständnis und ihre Geduld während der Zeit der
Erstellung dieser Arbeit bedanken.
Bochum, im November 1998
Helge Moritz
INHALTSVERZEICHNIS
V
Inhaltsverzeichnis
Vorwort
III
Nomenklatur
VIII
1 Einleitung
1
2 Grundlagen der Lichtstreuung
4
2.1
Die Raman-Streuung
5
2.1.2 Historisches, Übersicht
5
2.1.2 Klassische Darstellung des linearen Raman-Effekts
6
Der Schwingungs-Raman-Effekt für ein zweiatomiges
homonukleares Molekül
6
Der Schwingungs-Raman-Effekt für ein mehratomiges Molekül 8
Der Rotations-Raman-Effekt
11
Das Termschema
11
2.1.3 Quantenmechanische Darstellung des Raman-Effekts
Einleitung
Die Polarisierbarkeitstheorie von Placzek
Die Energieniveaus der Schwingungen
Die Besetzung von Schwingungsniveaus
Die Intensität des Raman-Streulichts der differentelle Ramanstreuquerschnitt
Der Einfluß der Flüssigphase
Der Rotations-Raman-Effekt
Abweichungen von den Näherungen
13
13
14
18
19
2.1.4 Anwendungen der Raman-Streuung
Temperaturbestimmung von Gasen
Messung von Konzentrationen
27
28
29
20
22
23
25
INHALTSVERZEICHNIS
VI
2.2
Die Mie-Streuung
Die Maxwellschen Gleichungen
Anwendung auf sphärische Partikel
Streuung an sphärischen Partikeln
Strukturresonanzen
32
33
35
37
39
2.3
Raman-Streuung an Mikropartikeln
Einführung
Modellierung
Geometrische Optik
Strukturresonanzen
Ramanstreuung bei Konzentrationsgradienten
Nichtlineare Effekte
44
44
44
45
46
50
55
3 Transportprozesse an Mikropartikeln
58
3.1
58
Einleitung
3.2
Transportprozesse innerhalb von Mikropartikeln
59
3.3
Transportprozesse mit Berücksichtigung der Gasphase
62
3.4
Dampfdruck
66
3.5
Die Löslichkeit von Gasen in Flüssigkeiten
68
3.6
Fazit
71
4 Der experimentelle Aufbau
Bisherige experimentelle Untersuchungen
74
74
4.1
Übersicht
76
4.2
Die Erzeugung einer Kette von Mikrotropfen
Einführung, Theorie
Der Schwingblendengenerator
Erfahrungen, Praxis
Kontrolle der Tropfenkette
79
79
82
86
87
4.3
Der optische Aufbau
91
4.3.1 Die Anregung zur Raman-Streuung
91
4.3.2 Die Detektionseinheit
Der Spektrograph
Die CCD-Kamera
92
92
93
4.3.3 Der Bildverstärker
Übersicht
94
94
INHALTSVERZEICHNIS
Beschreibung der Einzelkomponenten
4.4
4.5
5.2
96
Meßdatenerfassung und Auswertung
100
4.4.1 Hard- und Software
100
4.4.2 Die zweidimensionale Spektroskopie
101
Weitere experimentelle Aufbauten
106
4.5.1 Das Versorgungssystem des SBG
106
4.5.2 Messung von Tropfengeschwindigkeit und -aufenthaltsdauer
Tropfengeschwindigkeit aus Beugungmuster
Doppellichtschrankenmethode
Tropfenaufenthaltsmessungen
111
112
113
115
4.5.3 Der Tropfenkettenmonitor
119
4.5.4 Strömungsvisualisierung
122
5 Messungen und Ergebnisse
5.1
VII
124
Die Partikelphase
124
5.1.1 Messung
124
5.1.2 Kalibrierung
126
5.1.3 Linienintensität
128
5.1.4 Auswertung
131
5.1.5 Ergebnisse
131
Die Gasphase
136
5.2.1 Messung
136
5.2.2 Auswertung
139
5.2.3 Ergebnisse
142
5.2.4 Fazit
144
6 Zusammenfassung und Ausblick
146
Anhänge:
A
Ramanspektren einiger Substanzen
B
Kalibrierung der Massendurchflußregler
150
157
Literaturverzeichnis
166
NOMENKLATUR
VIII
Nomenklatur
Lateinische Großbuchstaben
Symbol
A
A, B, C, D
A1, A2
An, Bn
B
r
B
B0
Bv
C
C
C
De
Dv
DAB
E
r
E
r
E0
F
Fv
G
r
H
H
I
I0
J
L
r
M
Bezeichnung
SI-Einheit
Fläche
m2
Dampfdruckkonstanten
Raman-Intensität in den spektralen Bereichen 1 bzw. 2 W/m2
Entwicklungskoeffizient
Wegkonstante
m
magnetische Induktion
Vs/m2
Rotationskonstante
cm-1
Rotationskonstante
cm-1
Effizienz
Mischungsverhältnis
Gaskorrekturfaktor
Dissoziationsenergie
cm-1
Rotationskonstante
cm-1
Diffusionskoeffizient von A in B
m2/s
Energie
J, 1/cm
elektrischer Feldvektor
V/m
Amplitude des einfallenden Feldes
V/m
Fläche
m2
Energie eines Rotationszustands
1/cm
Energie eines Schwingungszustands
1/cm
magnetischer Feldvektor
A/m
Henry-Koeffizient
N/m2
Strahlungsflußdichte
W/m2
einfallende Strahlungsflußdichte
W/m2
Rotationsquantenzahl
Korrekturfaktor für das lokale Feld
Lösung der vektoriellen Wellengleichung
NOMENKLATUR
IX
MJ
r
N
N
N
NA
Nn
P
P
Pnl
r
P
r
Pfi
magnetische Quantenzahl
Lösung der vektoriellen Wellengleichung
Molekülanzahl
Anzahl der Atome eines Moleküls
Avogadro-Konstante
Anzahl der Moleküle im Zustand n
Druck, Partialdruck
Strahlungsleistung
Legendre-Polynom
S
T
V
V
Korrekturfaktor der molekularen Struktur
Temperatur
Volumen
Vergrößerung der Abbildung
Dipolmomentoperator
Amplitude des Übergangsmoments
1/mol
N/m2
W
Cm
Cm
K
m3
Lateinische Kleinbuchstaben
a
Partikelradius
m
a
Abstand zweier Doppeldioden
m
a, b, c, d
relative Signalanteile
an
isotroper Anteil des Polarisierbarkeitstensors
Asm/V
an
Mie-Koeffizienten der gestreuten Felder
b
Partikelradius, Sprungstelle der Gewichtungsfunktion
m
bn
Mie-Koeffizienten der gestreuten Felder
bv n
Nullpunktsamplitude der Normalschwingung n
c
c
c0
cP
c∗A
cn
r
c
d
d
dn
f
f
f
fP
Lichtgeschwindigkeit
molare Dichte, Konzentration
Anfangskonzentration
spezifische isobare Wärmekapazität
scheinbare mittlere Konzentration der Spezies A
Mie-Koeffizienten der inneren Felder
konstanter Vektor
Durchmesser
Abstand der Beugungsstreifen
Mie-Koeffizienten der inneren Felder
Freiheitsgrad
Brennweite
Frequenz, AnregungsGeometriefaktor für die Ramanstreuung
m/s
mol/l
mol/l
J/kg K
mol/l
m
m
m
Hz
NOMENKLATUR
X
g
gi
h
h
ir
k
k
k
k0
l
l
m
m
r
n
n
n
n
n
r
p
r
pind
r
p perm
Normschwerebeschleunigung
Grad der Entartung
Plancksches Wirkungsquantum
h = h/2π
imaginäre Einheit i2 = -1
Wellenvektor
Boltzmannkonstante
Löslichkeitskoeffizient, temperaturabhängig
Wellenzahl im Vakuum
Ordnung einer Resonanz
Länge, Abstand zwischen Partikelmittelpunkten
Masse
komplexer Brechungsindex
Einheitsvektor / Normalenvektor
ganzzahlige Ordnung diverser Funktionen
Modennummer einer Resonanz
Brechungsindex
Besetzungszahl, relative Anzahl
Dipolmoment
induziertes Dipolmoment
permanentes Dipolmoment
p
q
qn
qn.0
r
r
r
s
t
v
v
w
x
x
x
z
zn
Druck
Abstand zwischen zwei Atomkernen
Normalschwingung eines Moleküls
Amplitude der Normalschwingung
Ortskoordinate / Radius
Ortsvektor
Abstand
Zeit
Schwingungsquantenzahl
Geschwindigkeit
Gewichtungsfunktion
Mieparameter
Gewichtungsfaktor
Molenbruch
Abstand zum Schwingblendengenerator
eine der sphärischen Besselfunktionen
m/s2
Ws2
Ws2
m-1
Ws/K
m-1
m
kg
Asm
Asm
Asm
N/m2
m
m
m
m
s
m/s
m
NOMENKLATUR
XI
Griechische Großbuchstaben
Φ
Ω
Ψ
Ψ
ψn
ξn
·
·⋅
·×
·2
Strahlungsleistung
Raumwinkel
Wellenfunktion
Lösung der skalaren Wellengleichung
Riccati-Besselfunktion erster Art
Riccati-Besselfunktion dritter Art
Gradient
Divergenz
Rotation
Laplace-Operator
W
sr
Griechische Kleinbuchstaben
α
α
α
αδε
α0
αM
Polarisierbarkeit
Winkel
Polarisierbarkeitstensor
Komponente des Polarisierbarkeitstensor
permanente Polarisierbarkeit
Amplitude der Polarisierbarkeitsänderung
β
ε
ε
ε0
εr
φ
γ
γ
γn
η
κ
λ
λ
µ
µ
µr
µ0
ν
Hyperpolarisierbarkeitstensor
Cm2/V
relativer Abstand zwischen Tropfen
absolute Dielektrizitätskonstante = εrε0
As/Vm
Elektrische Feldkonstante
As/Vm
Dielektrizitätszahl
Ortskoordinate / Streuwinkel
rad
Oberflächenspannung
J/m2
zweiter Hyperpolarisierbarkeitstensor
Cm2/V
anisotroper Anteil des Polarisierbarkeitstensors
Asm/V
Wechselwirkungsparameter
Diffusionskoeffizient oder Temperaturleitfähigkeit
m2/s
Wellenlänge, Störm
3
Löslichkeitskoeffizient
Nm /Tonne at
reduzierte Masse
= µ0µr, absolute magnetische Permeabilität
Vs/Am
relative magnetische Permeabilität
magnetische Feldkonstante im Vakuum
Vs/Am
Wellenzahl
cm-1
Cm2/V
rad
2
Cm /V
Cm2/V
Cm2/V
Cm2/V
NOMENKLATUR
XII
~
ν
ν
θ
ρ
ρ
ρn
σ
σ
σ
τ
ω
ωe
ωexe, ωeye
ωn
Wellenzahl-, Ramanverschiebung
Frequenz
Ortskoordinate / Streuwinkel
Ladungsdichte
Substanzdichte
Polarisationsgrad
totaler Streuquerschnitt
elektrische Leitfähigkeit
Standardabweichung
charakteristische Zeit
Kreisfrequenz
Schwingungsfrequenz eines Moleküls
Anharmonizitätskonstanten
Eigenfrequenz der Normalschwingung
Indizes
∞
0
A, B
AS
c
D
e
e
el., e
EP
f
fl
g
ges
i
i
inc
kal, K
l
LM
max
min
n
n
Unendlich
einfallend
Spezies, Stoff
Anti-Stokes
kritisch, critical
Diffusion
gerade, even
Gleichgewicht, equilibrium
elektronisch
Einzelpartikel
Enzustand, final
flüssig
gasförmig
gesamt
Anfangszustand, initial
Laufvariable
einfallend, incident
kalibriert
Ordnung einer Resonanz
Lösungsmittel
maximal
minimal
= 3N-f, Freiheitsgrad
Modennummer einer Resonanz
cm-1
Hz
As/m3
kg/m3
m2
A/Vm
s
Hz
cm-1
cm-1
Hz
NOMENKLATUR
N
o
obs
opt
P
rot, r
res
s
S
S
sca, s
shift
t
t
TK
vibr., v
vp
XIII
Norm...
ungerade, odd
beobachtet, observiert
optimal
Partikel
Rotation
resonant
Strahl, FlüssigkeitsStandard
Stokes
gestreut, scattered
Verschiebung
transmittiert
Tropfen
Tropfenkette
Vibration
Dampf, vapor
Konstanten (aus Handbook of chemistry and physics [LID 92]):
Lichtgeschwindigkeit im Vakuum
Normschwerebeschleunigung
Magnetische Feldkonstante
Elektrische Feldkonstante
Plancksches Wirkungsquantum
Drehimpulsquantum
Boltzmann-Konstante
Avogadro-Konstante
Gaskonstante
c =
g =
µ0 =
ε0 =
h =
h =
k =
NA =
R =
2.997 924 58 . 108 m/s
9.806 65 m/s2
12.566 370 614 . 10-7 As/Vm
8.854 187 817 . 10-12 As/Vm
6.626 175 5 . 10-34 Js
h/2π = 1.054 572 66 . 10-34 Js
1.380 658 . 10-23 J/K
6.022 136 7 . 1023 mol-1
8.314 510 J/(mol K)
1. EINLEITUNG
1
1 Einleitung
Aerosole und Sprays, also Systeme aus gasgetragenen flüssigen oder festen
Mikropartikeln, spielen eine bedeutende Rolle in vielen natürlichen und technischen
Prozessen. Aufgrund ihrer großen Oberfläche, relativ zum Volumen, haben sie
besondere physikalische und chemische Eigenschaften, die den Energie- und
Stoffaustausch mit der Umgebung empfindlich beeinflußen. Beispiele hierfür sind die
Gemischaufbereitung in Verbrennungsprozessen, die Reinigung von Gasen in der
chemischen Verfahrenstechnik, die Medikamentierung lungengängiger Arzneimittel und
Trocknungsprozesse in der Lebensmittel- und Baustoffindustrie. Ferner sind Aerosole
für das lokale und globale Klima von Bedeutung.
Die experimentelle Untersuchung von Energie- und Stofftransportprozessen in
Aerosolen und Sprays ist von großer Bedeutung, selbst wenn die Berechnung solcher
Prozesse weitere Fortschritte macht. Notwendig sind die experimentellen Untersuchungen nicht nur für die Überprüfung der theoretischen Ansätze und deren
Weiterentwicklung; sie sind auch deswegen von Bedeutung, weil sich in Mikrotropfen
Zustände einstellen können (Übersättigung, Unterkühlung), die bei Proben, die mit
festen Wänden in Kontakt sind, nicht beobachtet werden. Eine Bestimmung der für die
Berechnung der Transportprozesse notwendigen Gleichgewichtskonzentration an der
Phasengrenze oder der Stoffeigenschaften im Tropfen auf andere Weise (Probennahme
mit anschließender Analyse), ist - im Gegensatz zur Untersuchung dieser Prozesse direkt
am Tropfen (in situ) - daher sehr problematisch. Bis jetzt ist dies mit keiner Meßtechnik
erreichbar.
1. EINLEITUNG
2
In dieser Arbeit wird eine optische Methode zur Bestimmung der instationären
Konzentrations- und Temperaturprofile in Tropfen und deren Umgebung realisiert: Mit
der zweidimensionalen Raman-Spektroskopie lassen sich zumindest in ausgewählten
Systemen diese Profile mit ausreichender Genauigkeit messen. Dies wird am Beispiel
des Desorptionsprozesses von Acetylen aus einer linearen Kette von Acetontropfen
demonstriert. Ein wesentlicher Aspekt ist dabei die Messung der Gaskonzentration
zwischen den Tropfen. Dazu wurde im Rahmen dieser Dissertation die gepulste
zweidimensionale Spektroskopie entwickelt. Es wird gezeigt, daß sich mit ihr die
Gasverteilung um Tropfen messen läßt, die sich durch eine Atmosphäre bewegen.
Für die Bestimmung der chemischen Konzentration innerhalb der Tropfen wird ein
spezielles Auswerteverfahren vorgestellt, mit der die radiale Gewichtung der
Streustrahlung aus den Tropfen festgestellt wird. Es zeigte sich nämlich, daß nicht alle
Bereiche innerhalb der Tropfen gleich viel zur Streustrahlung beitragen. Tritt ein
Konzentrationsgradient auf, wie es bei Transportprozessen immer der Fall ist, so würden
bei Nichtberücksichtigung dieser Gewichtung falsche mittlere Konzentrationen ermittelt
werden. In dieser Arbeit wird gezeigt, daß das meiste Streulicht aus den oberflächennahen Bereichen der Tropfen kommt.
Bei der Erstellung dieser Arbeit wurde versucht, die zum Teil komplexen
Zusammenhänge leicht verständlich, aber dennoch so vollständig wie möglich
darzustellen. Zusätzlich wurde Wert darauf gelegt, daß man sich mit der zitierten
Literatur einen guten Überblick über aktuelle ähnliche Arbeitsgebiete verschaffen kann.
Mit der Beschreibung der Grundlagen der Lichtstreuung beginnt das Kapitel 2. Hier
wird zunächst die Raman-Streuung klassisch und quantenmechanisch vorgestellt, um
dann auf die Lichtstreuung an sphärischen Partikeln überzuleiten: Die Mie-Streuung und
die Raman-Streuung an sphärischen Mikropartikeln. Im Kapitel 3 werden die
Transportprozesse an Mikropartikeln und die damit verbundenen Begriffe erläutert.
Kapitel 4 beschreibt detailliert den Versuchsaufbau. Zunächst wird hier die Erzeugung
der Tropfenkette mit einem Schwingblendengenerator und dessen Funktionsweise
dargestellt.
Danach
wird
der
optische
Aufbau
vorgestellt,
um
dann
zur
Meßdatenerfassung und Auswertung zu kommen. Hier wird auch die zweidimensionale
1. EINLEITUNG
3
Raman-Spektroskopie erläutert. Zum Schluß dieses Kapitels werden noch einige
kleinere Zusatzaufbauten beschrieben. Kapitel 5 betrifft die Messungen und daraus
gewonnene Ergebisse. Dabei werden die Messungen, die Auswertungen sowie die
Ergebnisse der Tropfenphase und der Gasphase getrennt voneinander beschrieben. Den
Abschluß dieser Arbeit bilden die Zusammenfassung und ein Ausblick.
2. GRUNDLAGEN DER LICHTSTREUUNG
4
2 Grundlagen der Lichtstreuung
Die Wechselwirkung zwischen Licht und Atomen, Molekülen oder einem von ihnen
gebildeten Verband wird unter anderem als Lichtstreuung bezeichnet. Durch sie ändern
sich im allgemeinen Intensität, Richtung und Polarisation des Lichtes. Dies kann durch
Reflexion, Brechung und Beugung des Lichts (Photonen) geschehen. Aber auch die
Energieentnahme von einer einfallenden Lichtwelle und die nachfolgende Wiederaustrahlung eines Teils der Energie wird Lichtstreuung genannt. Wesentlich für diese
Form der Lichtstreuung ist, daß die durchstrahlte Materie für das einfallende Licht eine
ungeordnete, körnige Struktur besitzt (einzelne Teilchen oder starke Inhomogenitäten).
Wird bei der Lichtstreuung nur der Impuls (Änderung der Richtung des gestreuten
Lichtes), nicht aber die Energie (Wellenlängenänderung des gestreuten Lichtes) des
Lichtes geändert, so spricht man von elastischer Lichtstreuung. Ändert sich neben dem
Impuls auch die Energie des gestreuten Lichtes, so handelt es sich um inelastische
Lichtstreuung. Kohärente Lichtstreuung liegt vor, wenn zwischen dem gestreuten Licht
verschiedener Streuteilchen eine feste Phasenbeziehung zum einfallenden Licht und
damit auch untereinander vorliegt, so daß sie miteinander interferieren und detektiert
werden können.
Je nach den theoretischen oder experimentellen Annahmen, unter denen die
Lichtstreuung jeweils beschrieben werden kann, wird zwischen verschiedenen Formen
der Lichtstreuung unterschieden
[Ber 93]
. Im Fall der inelastischen Lichtstreuung können
dies die Raman-, Brillouin- und die Compton-Streuung sein. Manchmal wird auch die
DIE RAMAN-STREUUNG
5
Fluoreszenz dazugezählt. Beispiele der elastischen Lichtstreuung sind die Mie-,
Rayleigh- und Resonanz-Streuung sowie der Tyndall-Effekt.
In den folgenden Abschnitten dieses Kapitels werden die Raman- und die MieStreuung behandelt.
2.1 Die Raman-Streuung
2.1.1 Historisches, Übersicht
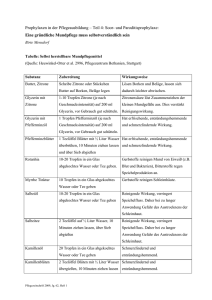
Der Raman-Effekt wurde 1923 von dem österreichischen Physiker Adolf Gustav
Stephan Smekal (daher auch manchmal Smekal-Raman-Effekt genannt) vorausgesagt
[SME 23]
. Der experimentelle Nachweis gelang 1926 [ARD 90] durch den indischen Physiker
Sir (seit 1929) Chandrasekhara Venkata Raman (Bild 2.1) und seinen Mitarbeitern
Krishnan und Venkateswaran
[RAM 28]
. Raman erhielt für diese Entdeckung 1930 den
Nobelpreis für Physik. Im selben Jahr wie Raman
veröffentlichten die beiden russischen Physiker
G.S. Landsberg
und
L.J. Mandelschtam
Nachweis des Raman-Effekts am Quarz
den
[LAN 28]
.
Zur Untersuchung des Raman-Effekts wurden bis
Mitte
der
intensiven
sechziger
Jahre
Spektrallinien
hauptsächlich
des
Quecksilbers
(QuecksilberhochdruckQuecksilberniederdrucklampen)
die
und
zur
Anregung
eingesetzt. Heute wird dazu fast ausschließlich
Laser-Strahlung verwendet.
Die praktische Anwendung des Raman-Effekts
findet sich in der Raman-Spektroskopie. Hierüber
existieren Monographien, von denen einige erwähnt
Bild 2.1: C. V. Raman.
2. GRUNDLAGEN DER LICHTSTREUUNG
6
seien: Schrader
Moser
[BRA 62]
[SCH 95]
, Long
[LON 77]
, Herzberg
und Anderson
[HER 91]
, Weber
[WEB 79]
, Brandmüller und
[AND 73]
. Über die Raman-Spektroskopie hinausgehende
Literatur, die einen guten Überblick über die Spektroskopie und Optik im allgemeinen
liefern, sind Demtröder
[SCH 94]
und Mayinger
[DEM 91]
, Bergmann-Schäfer
[MAY 94]
[BER 93]
, Hollas
[HOL 95]
, Schmidt
zu erwähnen.
2.1.2 Klassische Darstellung des linearen (spontanen) RamanEffekts
Das Erscheinungsbild des Raman-Effekts liegt im Auftreten von schwachen Linien
im
Spektrum,
die
relativ
zur
Anregungswellenlänge
frequenz-
bzw.
wellenlängenverschoben sind. Diese Linien sind charakteristisch für die streuenden
Moleküle (Gase, Flüssigkeiten oder Kristalle) und deren thermodynamischen Zustand
(z.B. der Temperatur). Die wesentlichen Merkmale der Raman-Streuung lassen sich am
einfachsten mit der klassischen Darstellung erklären.
Der Schwingungs-Raman-Effekt für ein zweiatomiges homonukleares Molekül 1
Fällt das elektrische Feld
r
r
E = E 0 cos( 2πν 0 t )
(2.1)
einer monochromatischen Lichtwelle auf die Elektronen eines Moleküls, werden diese
gegen die sehr viel schwereren Kerne in Schwingung versetzt (ν0 Frequenz der
Lichtwelle). Es entsteht ein oszillierender Dipol mit dem elektrischen Dipolmoment
r
r
p = αE .
1
(2.2)
Das einfachste Modell eines Moleküls ist das zweiatomige homonukleare Molekül, das auch Hantel-
Modell genannt wird. Darunter versteht man ein System (Molekül), das aus zwei Massenpunkten
(Atomen) besteht, die durch einen masselosen Stab verbunden sind. Beispiele hierfür sind das
Stickstoffmolekül N2 und das Sauerstoffmolekül O2.
DIE RAMAN-STREUUNG
7
α ist die Polarisierbarkeit des Moleküls und hängt von der Wellenlänge des einfallenden
Lichts sowie vom Bindungszustand und den Symmetrieeigenschaften des Moleküls ab.
Schwingen die Kerne der Moleküle gegeneinander, so kann sich die Polarisierbarkeit
mit der Molekülfrequenz νM ändern:
α = α 0 + α M cos( 2πν M t ) .
(2.3)
Hier sind α0 die mittlere (permanente) Polarisierbarkeit und αM die Amplitude der
Polarisierbarkeitsänderung des Moleküls. Setzt man die Gln. 2.1 und 2.3 in Gl. 2.2 ein
und formt die trigonometrischen Beziehungen um [BRO 81, S.233], so erhält man
r
r
p = α 0 E0 cos( 2πν 0 t )
r
+ 1 2 α M E0 {cos[2π( ν 0 − ν M )t ] + cos[2π( ν 0 + ν M )t ]} .
(2.4)
Das elektrische Dipolmoment enthält nunmehr drei Frequenzen, die das Molekül auch
emittiert. Der erste Term beschreibt die elastische Streuung mit der Frequenz ν0 des
einfallenden Lichtes. Dieser Fall entspricht der Rayleigh-Streuung. Im zweiten und
dritten Term treten die Frequenzen
νS = ν 0 − ν M
und
(2.5)
ν AS = ν 0 + ν M
(2.6)
auf, die der Stokes- bzw. Anti-Stokes-Frequenz der Raman-Streuung entsprechen.
Die totale Strahlungsleistung Φ eines schwingenden Dipols ergibt sich nach der
r
klassischen Elektrodynamik [JAC 83, LON 77] aus dem Dipolmoment p (Gl. 2.4) zu
Φ =
(ε0:
1
ω4 r2
p
4 πε 0 3 c 3
Dielektrizitätskonstante
Kreisfrequenz).
im
(2.7)
Vakuum,
c:
Lichtgeschwindigkeit,
ω = 2πν:
2. GRUNDLAGEN DER LICHTSTREUUNG
8
Der Schwingungs-Raman-Effekt für ein mehratomiges Molekül
Betrachtet man Moleküle mit mehr als zwei Atomen, so müssen die Lagen und
Schwingungen der Atome untereinander berücksichtigt werden. Ein Molekül mit
N Atomen besitzt 3N-f Freiheitsgrade (f=5 für lineare und f=6 für nichtlineare Moleküle)
für die Schwingungen der Atomkerne. Jede Bewegung eines Moleküls kann als
Kombination
dieser
unabhängigen
Schwingungen,
den
sogenannten
Normal-
schwingungen, zerlegt werden. Die verschiedenen Normalschwingungen liefern zu einer
Bewegung unterschiedliche Beiträge. Sind die Schwingungsamplituden klein, so können
die Moleküle als harmonische Oszillatoren aufgefaßt werden. Jede Normalschwingung
kann dann wie folgt durch Normalkoordinaten qn ausgedrückt werden:
qn ( t ) = qn,0 cos( ω n t )
mit
ω n = 2πν n .
(2.8)
Hier sind ω n die Eigenfrequenzen der Schwingungen und qn,0 deren Amplituden.
Weiterhin ist die Polarisierbarkeit richtungsabhängig und kann nicht mehr als Skalar
(s. Gl. 2.2) betrachtet werden, wie es nur für isotrope Moleküle möglich ist, sondern
muß als Tensor zweiter Stufe ( α ) beschrieben werden. Dessen Komponenten (αδε)
hängen von der Molekülsymmetrie ab. Das induzierte Dipolmoment ergibt sich damit zu
r
r
pind = α E .
(2.9)
Existiert ein bereits vorhandenes permanentes Dipolmoment, so ergibt sich das gesamte
Dipolmoment zu
r
r
r
p = pperm + pind .
(2.10)
Unter der obigen Voraussetzung kleiner Schwingungsamplituden lassen sich das
permanente Dipolmoment und die ortsabhängigen Komponenten der Polarisierbarkeit
α in eine Taylorreihe nach den Normalkoordinaten qn um die Gleichgewichtslage des
Moleküls (qn=0) entwickeln, die nach dem ersten Glied abgebrochen wird:
r
r
pperm = pperm (qn = 0) +
3N − f
∑
n =1
r
⎛ ∂pperm ⎞
⎜
⎟
⎝ ∂qn ⎠ q
qn + ...
n
=0
(2.11)
DIE RAMAN-STREUUNG
9
3N − f
∑
α δε = α δε ( qn = 0) +
n =1
⎛ ∂α δε ⎞
⎜
⎟
⎝ ∂qn ⎠ q
qn + ...
n
(2.12)
=0
Setzt man die Gln. 2.1, 2.8, 2.9, 2.11 und 2.12 in Gl. 2.10 ein, so erhält man für das
gesamte zeitabhängige Dipolmoment
r
r
p( t ) = pperm (qn = 0)
3N − f
+
∑
n =1
r
⎛ ∂pperm ⎞
⎟
⎜
⎝ ∂qn ⎠ q
permanent
qn,0 cos(ω n t )
n
infrarot
=0
r
+ α ( qn = 0) E0 cos(ω 0 t )
elastisch
⎡
⎤
r
⎛ ∂α ⎞
1
E0 qn,0 ⎢cos(ω 0 − ω n )t + cos(ω 0 + ω n )t ⎥ .
+
⎜
⎟
244
3 144244
3⎥
2 n =1 ⎝ ∂qn ⎠
⎢⎣ 144
qn = 0
Stokes
Anti − Stokes ⎦
144444444444424444444444443
3N − f
∑
Raman
(2.13)
Gl. 2.13 zeigt (wie auch schon in Gl. 2.4 gesehen), daß eine einfallende
monochromatische Lichtwelle mit der Frequenz ω0 ein Dipolmoment in den Molekülen
erzeugt, in dem weitere Frequenzen auftreten. In diesen Frequenzen können die
Moleküle auch wieder Licht (elektromagnetische Strahlung) abstrahlen. Der erste Term
entspricht dem permanten (mittleren) Dipolmoment, das nicht zum Streulicht beiträgt.
Die übrigen Terme dieser Gleichung beschreiben unterschiedliche Beiträge der
Moleküle zum Streulicht: Term 2 trägt zur Absorption von Infrarot-Strahlung bei. Daher
werden üblicherweise Infrarot-Spektren in Absorption aufgenommen und die
Transmission über der (absoluten) Wellenzahl aufgetragen. Die hier auftretenden
Frequenzen stammen von den Eigenfrequenzen ω n der Moleküle. Voraussetzung ist
r
allerdings ein sich änderndes Dipolmoment ([∂pperm ∂qn ]q n = 0 ≠ 0) . Homonukleare
zweiatomige Moleküle haben deshalb kein Infrarot-Spektrum. Term 3 entspricht dem
2. GRUNDLAGEN DER LICHTSTREUUNG
10
gewöhnlichen Hertz´schen Dipol2 bzw. der elastischen (Rayleigh-) Streuung mit der
einfallenden Frequenz ω
0.
Die Raman-Streuung wird durch den letzten Term
beschrieben. Hier treten die beiden Mischfrequenzen auf, die sich um ± ω
n
zur
einfallenden Frequenz ω 0 unterscheiden. Bei der Erhöhung der Frequenz um ω n spricht
man von Anti-Stokes-Raman-Linien und bei der Erniedrigung um denselben Betrag von
Stokes-Raman-Linien.
Man
sieht,
daß
das
Raman-Spektrum
nur
von
der
Frequenzverschiebung und nicht von der Frequenz des einfallenden Lichts abhängt. Mit
anderen Worten, die Messung eines Raman-Spektrums ist von der Anregungsfrequenz
(oder -wellenlänge) unabhängig.3 Üblicherweise hat man es in der Raman-Spektroskopie
ν (oder auch Wellenzahl- bzw. Ramanverschiebung
mit der Wellenzahldifferenz ∆~
genannt) zu tun, die wie folgt definiert ist:
ω0 − ωn
∆ν
∆ω
1
1
∆~
ν =
=
=
=
−
c
λ0 λn
2π c
2π c
(2.14)
Hier ist c die Lichtgeschwindigkeit und λ die Wellenlänge. Die Einheit der Wellenzahl
ist cm-1.
Notwendig für das Auftreten von Raman-Streuung ist eine Änderung des
Polarisierbarkeitstensors mit den Normalkoordinaten ([∂α ∂qn ]q n = 0 ≠ 0) . Ob ein
Molekül Raman-aktiv oder infrarot-aktiv ist, hängt also von unterschiedlichen
physikalischen Phänomenen ab. Für Strukturuntersuchungen von Molekülen ergänzen
sich die beiden Spektroskopiearten.
2
Beim Hertz´schen Dipol handelt es sich um zwei entgegengesetzt geladene, gleichgroße elektrische
Ladungen, deren Ladungsschwerpunkte sich mit der Frequenz ω0 periodisch ändern. Dabei werden
elektromagnetische Wellen abgestrahlt.
3
Zur Überprüfung, ob eine Linie durch Raman-Streuung oder einen anderen Streumechanismus, z.B.
Fluoreszenz, entstanden ist, können die Spektren einer Substanz bei zwei verschiedenen Anregungswellenlängen erzeugt werden. Die Linien des Raman-Spektrums werden bei derselben Frequenz- oder
Wellenzahlverschiebung erscheinen. Fluoreszenzspektren werden sich im allgemeinen bei Anregungen
durch verschiedene Wellenlängen unterscheiden.
DIE RAMAN-STREUUNG
11
Der Rotations-Raman-Effekt
Die vorhergehenden Betrachtungen über das Auftreten von Raman-Linien beziehen
sich auf die Schwingungen bzw. Vibrationen zwischen den Atomkernen der Moleküle.
Man spricht daher auch vom Vibrations-Raman-Effekt. Die Polarisierbarkeit kann sich
jedoch auch bei der Rotation des Moleküls ändern und man erhält den Rotations-RamanEffekt. Der Formalismus zu dessen Beschreibung ist derselbe, jedoch ändert sich die
Polarisierbarkeit mit der doppelten Rotationsfrequenz. Meistens treten Vibrationen und
Rotationen gleichzeitig auf und man erhält den Rotations-Vibrations-Raman-Effekt.
Termschema
Ein Termschema, in dem die Energieniveaus eines Moleküls aufgetragen sind,
verdeutlicht die möglichen Raman-Übergänge. Das in Bild 2.2 dargestellte Termschema
zeigt zwei Schwingungsniveaus (v = 0 und 1), wobei jedem Schwingungsniveau
Rotationsniveaus (hier nur die ersten 5 Rotationsniveaus J = 0 bis 4 eingezeichnet)
überlagert sind. In einer vereinfachten Darstellung kann man sich die Anregung zur
Raman-Streuung so vorstellen, daß das Molekül durch den Laserstrahl in ein virtuelles
Niveau (gestrichelte Linie) angehoben wird. Nach einer kurzen Lebensdauer relaxiert
das Molekül in einen niedrigeren Zustand, wobei ein Photon emittiert wird. Je nachdem,
in welches Niveau das Molekül dabei übergeht, wird der Übergang bezeichnet: Ramanoder Rayleighstreuung, Stokes- oder Anti-Stokes-Übergang, Schwingungs- oder
Rotationsübergang oder eine Kombination davon.
Die hier dargestellte klassische Beschreibung des Raman-Effekts kann das Auftreten
von zusätzlichen Frequenzen (Linien) im Streulicht richtig vorhersagen, nicht jedoch
deren Intensität. Besonders der Unterschied zwischen den Intensitäten der Stokes- und
der Anti-Stokes-Linien ist nicht erklärbar. Hierzu muß das Molekül mit seinen
Energiezuständen quantenmechanisch beschrieben werden.
2. GRUNDLAGEN DER LICHTSTREUUNG
12
Bild 2.2: Vereinfachte Darstellung der Raman-Übergänge in einem Termschema.
Mit v sind die Vibrations- und mit J die Rotationsniveaus gekennzeichnet.
DIE RAMAN-STREUUNG
13
2.1.3 Quantenmechanische Darstellung des Raman-Effekts
Einleitung
Eine vollständige Beschreibung mikrophysikalischer Systeme, wie sie z.B. Moleküle,
Atome und Atomkerne bilden, ist mit den Methoden der klassischen Physik nicht
möglich. Dazu sind die Methoden der Quantenmechanik nötig, die berücksichtigt, daß
das mikrophysikalische Geschehen nicht stetig, sondern sprunghaft (gequantelt) ist. So
ändert sich der Energieinhalt eines mikrophysikalischen Systems nicht kontinuierlich,
sondern nur portionsweise um den Betrag hν (h Planck´sches Wirkungsquantum,
ν Frequenz), oder das Vielfache davon. Mikrophysikalische Systeme können daher nur
ganz bestimmte (diskrete) Energiestufen oder -zustände einnehmen. Die energetische
Breite der Energiezustände ∆E hängt von der mittleren Lebensdauer τ des Zustands ab
und wird durch die Heisenberg´sche Unschärferelation ∆E ⋅ τ ≥ h 2
(h = h 2π )
beschrieben. Durch diese Unbestimmtheit eines Anfangszustandes wird eine exakte
Vorausberechnung mikrophysikalischer Systeme unmöglich. Die Quantenmechanik
bedient sich daher statistischer Methoden zu deren Beschreibung und berechnet
(Übergangs-)
Wahrscheinlichkeiten.
Dort
sind
die
Energiezustände,
die
ein
Mikroteilchen einnehmen kann, durch Wellenfunktionen ψ festgelegt (Welle-TeilchenDualismus).
Das
Quadrat
des
Betrages
dieser
Wellenfunktion
gibt
die
Wahrscheinlichkeitsdichte an, mit der sich das Mikroteilchen zu einer bestimmten Zeit
an einem bestimmten Ort befindet. Ändert sich der Energiezustand eines Mikroteilchens,
z.B. durch Emission oder Absorption von Strahlung, so wird der Übergang von der
ursprünglichen
Wellenfunktion Ψi
Wellenfunktion Ψf
(final
state,
(initial
state,
Endzustand)
Anfangszustand)
durch
die
zur
neuen
Amplitude
Übergangsmoments definiert:
r
Pfi =
r
Ψ f P Ψi =
∫
r
Ψ *f P Ψi d 3 x .
(2.15)
des
2. GRUNDLAGEN DER LICHTSTREUUNG
14
Die Klammerdarstellung wird Diracsche-Braket-Notation genannt. Die neue Wellenr
funktion ist komplex konjugiert. P ist der Dipolmomentoperator und das Integral
erstreckt sich über die Raumkoordinaten d3x.
Die Polarisierbarkeitstheorie von Placzek
Die quantenmechanische Beschreibung des Raman-Effekts wurde erstmals von
Placzek [PLA 34] durchgeführt. In seiner semiklassischen Polarisierbarkeitstheorie wird die
elektromagnetische Strahlung weiterhin klassisch als Dipolstrahlung behandelt, das
Molekül jedoch quantenmechanisch. Eine Vereinfachung der quantenmechanischen
Beschreibung des Moleküls läßt sich erreichen, indem die Gesamtwellenfunktion, die
den Zustand eines Moleküls beschreibt, faktorisiert wird (Born-OppenheimerNäherung) [BOP 27]:
Ψ = Ψel (qe , qn ) ⋅ Ψvibr (qn ) ⋅ Ψrot (qn ) .
(2.16)
Die Gesamtwellenfunktion kann also in Einzelwellenfunktionen aufgespalten werden,
wenn diese (näherungsweise) unabhängig voneinander sind. Die elektronische
Wellenfunktion Ψel ist abhängig von den Elektronenkoordinaten qe und den
Normalkoordinaten qn der Kerne, während die Vibrationswellenfunktion Ψvibr und die
Rotationswellenfunktion Ψrot nur von den Normalkoordinaten abhängen. Durch die
Aufspaltung der Gesamtwellenfunktion können die Einzelwellenfunktionen getrennt
voneinander betrachtet werden.
Für die Beschreibung des Vibrations-Raman-Effekts betrachtet man nur die
r
Vibrationswellenfunktion Ψv 1 und ersetzt den Dipolmomentoperator P in Gl. 2.15
durch
den
induzierten
Dipolmomentoperator
(Gl. 2.9).
Man
erhält
für
Übergangsmoment
r
Pfi =
1
Ψv f
r
α Ψv i ⋅ E 0 .
(2.17)
Im Folgenden wird die Indizierung von vibr und rot nur durch die Anfangsbuchstaben durchgeführt.
das
DIE RAMAN-STREUUNG
15
Die Matrixelemente des Polarisierbarkeitstensors α fi für den Übergang f ← i sind
bestimmt durch
(α δε ) fi =
Ψv f α δε Ψv i .
(2.18)
Jede Komponente des Polarisierbarkeitstensors kann, wie in der klassischen Betrachtung
(Gl. 2.12), in eine Taylorreihe nach den Normalkoordinaten qn um die Gleichgewichtslage des Moleküls (qn=0) entwickelt werden:
(α δε ) fi = (α δε ) q n = 0 Ψv f Ψv i
+
∑
n
⎛ ∂α δε ⎞
⎟
⎜
⎝ ∂qn ⎠ q
n
=0
Ψv f qn Ψv i
+ ... .(2.19)
Auch hier wurde die Taylorreihe nach dem linearen Glied abgebrochen.
Der Schwingungszustand eines Moleküls kann in erster Näherung durch einen
harmonischen Oszillator dargestellt werden. Die Vibrationswellenfunktion kann dann
als
Produkt
der
Wellenfunktionen
des
harmonischen
Oszillators
für
jede
Normalkoordinate dargestellt werden. Die Vibrationswellenfunktionen des Anfangsund Endzustandes lassen sich dann wie folgt schreiben:
∏
Ψv i =
Ψv i,n (qn )
n
Ψv f =
∏
(2.20)
Ψv f ,n ( qn )
n
mit n = 1, ... , 3N-f . Die Größen vf,n und vi,n werden Schwingungsquantenzahlen genannt
und können nur ganzzahlige Werte annehmen. Setzt man Gl. 2.20 in Gl. 2.19 ein, so
erhält man
(α δε ) fi = (α δε ) q n = 0
∏ Ψv
f ,n
( qn )
n
+
∑
n
⎛ ∂α δε ⎞
⎜
⎟
⎝ ∂qn ⎠ q
∏
Ψv i,n ( qn )
n
n
=0
∏ Ψv
n
f ,n
( qn ) qn
∏
n
Ψv i ,n (qn ) . (2.21)
2. GRUNDLAGEN DER LICHTSTREUUNG
16
Gl. 2.21 läßt sich aufgrund der Eigenschaften der Wellenfunktionen des harmonischen
Oszillators vereinfachen. Einzelheiten dazu sind aus den Standardmonographien über
die Quantenmechanik [z.B. MES 76, GRE 84] zu entnehmen. Das Skalarprodukt des ersten
Terms verschwindet nur dann nicht, wenn Anfangs- und Endzustand identisch sind:
∏ Ψv ∏
f ,n
n
Ist für alle n
⎧0
= ⎨
⎩1
Ψv i,n
n
für v f , n ≠ v i , n
für v f , n = v i , n
.
(2.22)
vf,n = vi,n , d.h. die Schwingungsquantenzahl ändert sich bei einem
Übergang nicht, liegt Rayleigh-Streuung vor. Für das Matrixelement des zweiten Terms
von Gl. 2.21 gilt folgende Fallunterscheidung:
∏ Ψv
f ,n
( qn ) qn
n
∏
Ψv i ,n (qn )
n
⎧
0
⎪
= ⎨bv n v f , n + 1
⎪ b
v f ,n
⎩ vn
für
für
v f ,n = vi ,n
für
v f ,n = vi ,n − 1
v f , n = v i , n + 1 ,(2.23)
wobei
bv n 2 =
h
(2.24)
8π 2 µν n
die Nullpunktsamplitude der Normalschwingung n mit der Frequenz νn und µ die
reduzierte Masse des Moleküls darstellt. bv n ist das quantenmechanische Analogon zur
Amplitude qn,o der Normalkoordinate in der klassischen Behandlung. Der zweite Term
von Gl. 2.21 beschreibt die Raman-Streuung. Soll die n-te Mode einen Beitrag zur
Raman-Streuung liefern, so muß sich bei einem Übergang die Vibrationsquantenzahl um
den Betrag 1 ändern (Auswahlregel):
v f ,n = vi ,n + 1
v f ,n = vi , n − 1
(Stokes − Streuung)
.
(Anti − Stokes − Streuung)
(2.25)
Zusätzlich darf kein Term des Produkts verschwinden. Dies wird erreicht, indem für alle
Moden, außer der n-ten Mode, die Vibrationsquantenzahl von Anfangs- und Endzustand
gleich sein müssen:
DIE RAMAN-STREUUNG
v f , j = vi , n
17
j≠n.
für
(2.26)
Weiterhin kommt als notwendige Bedingung hinzu, daß mindestens eine Komponente
des abgeleiteten Polarisierbarkeitstensors ungleich Null ist.
Für die Matrixelemente des Polarisierbarkeitstensors folgt dann:
⎛ ∂α ⎞
(α δε ) v i ,n +1, v i ,n = ⎜ δε ⎟
⎝ ∂qn ⎠ q
⎛ ∂α ⎞
(α δε ) v i ,n −1, v i,n = ⎜ δε ⎟
⎝ ∂qn ⎠ q
n
n
=0
=0
bv n
v i, n + 1 (Stokes-Streuung)
bv n
v i, n
(2.27)
(Anti-Stokes-Streuung) . (2.28)
Man erhält also je einen Polarisierbarkeitstensor für den Stokes- und den Anti-StokesFall, die, verknüpft mit den Gln. 2.9, 2.7 und 2.14, die totale Strahlungsleistung Φ für
ein Molekül und eine Molekülschwingung liefern:
2
ΦS =
ν S4 ⎛ ∂α δε ⎞
1 16π 4 ~
bv2n ( v i , n + 1) E 02
⎜
⎟
3
4 πε 0
⎝ ∂q n ⎠ q = 0
3c
n
(2.29)
2
Φ AS
ν 4AS ⎛ ∂α δε ⎞
1 16π 4 ~
bv2n v i , n E 02
=
⎜
⎟
3
4 πε 0
⎝ ∂q n ⎠ q = 0
3c
n
(2.30)
Die Indizes S und AS stehen entsprechend für den Stokes- bzw. den Anti-Stokes-Fall.
Ersetzt man die Amplitude des elektrischen Feldes durch die Strahlungsflußdichte2
I0 =
1 ε0
1
E 02 = cε 0 E 02 ,
2 µ0
2
(2.31)
so erhält man
2
Häufig auch Intensität (SI-Einheit W/m2) genannt; manchmal auch mit dem Formelzeichen D
bezeichnet.
2. GRUNDLAGEN DER LICHTSTREUUNG
18
2
ΦS
⎛ ∂α ⎞
= const . ⋅ ~
ν S4 I 0 ⎜ δε ⎟
⎝ ∂q n ⎠ q
n
=0
bv2n ( v i , n + 1)
(2.32)
bv2n vi , n
(2.33)
2
Φ AS
⎛ ∂α ⎞
= const . ⋅ ~
ν 4AS I 0 ⎜ δε ⎟
⎝ ∂q n ⎠ q
n
=0
mit einer Zusammenfassung der Konstanten:
1
const . =
8π 3 µ 02
3
3c 3ε 02
.
(2.34)
Aus den Gln. 2.32 und 2.33 sieht man, daß sich die Strahlungsleistung für den Stokesund den Anti-Stokes-Fall unterscheiden. Diese Unterscheidung wird in der klassischen
Betrachtung des Raman-Effekts nicht gemacht.
Die Energieniveaus der Schwingungen
Eine weitere schon oben gemachte Unterscheidung ist, daß die Schwingungen des
Moleküls nur ganz bestimmte Energien bzw. Energiezustände / -niveaus einnehmen. Die
energetische Lage des Schwingungszustands mit der Schwingungsquantenzahl v unter
Annahme einer harmonischen Schwingung für ein zweiatomiges Molekül ist,
ausgedrückt in Schwingungstermen [HER 91]:
G ( v) =
Ev
1⎞
⎛
= ωe ⎜ v + ⎟
⎝
hc
2⎠
.
(2.35)
Hier ist Ev die Energie des Schwingungszustands v und ω e = νn/c die Schwingungskonstante des Moleküls in Wellenzahlen.
DIE RAMAN-STREUUNG
19
Die Besetzung von Schwingungsniveaus
In der Spektroskopie werden im allgemeinen nicht einzelne Moleküle untersucht,
sondern ein Ensemble von N Molekülen pro Volumeneinheit. Die Besetzung von
Energieniveaus ist für die Moleküle statistisch und abhängig von der Temperatur. Dies
wird im thermischen Gleichgewicht durch das Boltzmannsche-Verteilungsgesetz
beschrieben:
Nn = N
gn
∑ gi e − E
i
kT
e
−
En
kT
.
(2.36)
i
Nn ist die Anzahl der Moleküle im Niveau n mit der Energie En. k ist die Boltzmann-
Konstante und T die Temperatur. Die Summe geht über alle Niveaus, die besetzt werden
können. gi ist der Grad der Entartung (Anzahl der Energieniveaus mit derselben Energie,
auch als statistisches Gewicht bezeichnet) des Niveaus i.
Betrachtet man nur Schwingungszustände, dann kann für alle Schwingungsniveaus
gi = 1 gesetzt werden und für En und Ei setzt man das entsprechende G(v) aus Gl. 2.35.
Damit erhält man die relative Anzahl nv (oder auch Besetzungszahl) der Moleküle im
Zustand Ev [LEI 84]:
nv =
Nv
=
N
1
∞
e
−
G ( v ) hc
kT
(2.37)
∑ e −G( v )hc kT
v =0
Für Stickstoff (ω e = 2360 cm-1) erhält man demnach bei Raumtemperatur (T = 293 K)
folgende Besetzungszahlen für die unteren drei Schwingungsniveaus: nv=0 = 99.9988 %,
nv=1 = 10-5, nv=2 = 10-10, ... . Man sieht, daß sich fast alle Stickstoffmoleküle im
Schwingungsgrundzustand befinden. Für die meisten anderen Moleküle bekommt man
qualitativ das gleiche Ergebnis. Eine Folge dieser ungleichmäßigen Besetzung der
Niveaus ist ein entsprechend seltener Anti-Stokes-Übergang, da sich dazu ein Molekül
mindestens im ersten Schwingungsniveau aufhalten muß.
2. GRUNDLAGEN DER LICHTSTREUUNG
20
Die Intensität des Raman-Streulichts - der differentielle Ramanstreuquerschnitt
Betrachtet man ein Ensemble von Molekülen, so ist die Intensität (Strahlungsflußdichte) des gestreuten Raman-Lichts in den Beobachtungsraumwinkel Ωobs wie folgt
definiert [MAY 94]:
I =
dσ n
Ω obs N v l I 0 .
dΩ
(2.38)
Der Ausdruck dσn/dΩ wird differentieller Streuquerschnitt genannt und beinhaltet die
oben erarbeiteten Ergebnisse bzgl. des Streuverhaltens. σn ist der totale Streuquerschnitt
für die Normalschwingung n mit der Wellenzahlverschiebung ~ν und l ist die Länge des
n
Beobachtungsvolumens. Gl. 2.38 gilt für eine gemittelte Intensität I0 der anregenden
Strahlung entlang l. Weiterhin wird angenommen, daß der differentielle Streuquerschnitt
im Beobachtungsraumwinkel Ωobs konstant ist. Für die experimentell häufig eingesetzte
90°-Geometrie3 wird der differentielle Streuquerschnitt von Schrader
[SCH 95]
wie folgt
angegeben:
(~
ν0 − ~
νn ) 4
h
⎛ dσ n ⎞
⎛ 2 7 2⎞
⎜ an + γ n ⎟
⎜
⎟ = 3 2 ~
~
⎝ dΩ ⎠ S
45 ⎠
2 cε 0 νn [1 − exp( − hcνn / kT )] ⎝
(2.39)
(~
ν0 + ~
νn ) 4
h
⎛ dσ n ⎞
⎛ 2 7 2⎞
= 3 2 ~
⎜ an + γ n ⎟ .
⎜
⎟
~
⎝ dΩ ⎠ AS
45 ⎠
2 cε 0 νn [exp( − hcνn / kT ) − 1] ⎝
(2.40)
bzw.
In den rechten Klammertermen der Gln. 2.39 und 2.40 wird die Änderung des
Polarisierbarkeitstensors in einen isotropen Anteil (an) und einen anisotropen Anteil (γn)
aufgespalten. Die Streuquerschnitte sind proportional zur 4. Potenz der Wellenzahlverschiebung. Deshalb soll die Wellenzahl der anregenden Strahlung ~ν möglichst groß
0
(bzw. deren Wellenlänge möglichst klein) sein, um einen möglichst großen Streuquerschnitt zu erhalten. Allerdings fluoreszieren viele Moleküle, wenn sie mit
3
Linear polarisiertes einfallendes Licht, Beobachtung bei 90° zum Polarsationsvektor und zur
Ausbreitungsrichtung des einfallenden Lichts.
DIE RAMAN-STREUUNG
21
ultraviolettem und blauem Licht angeregt werden, was zu einer ungünstigen
Überlagerung des Raman-Spektrums mit der Fluoreszenz führt. Wird von der 90°Geometrie abgewichen, so muß den Gln. 2.39 und 2.40 der Faktor
2ρn + (1 − ρn ) sin 2 Θ
1 + ρn
(2.41)
hinzugefügt werden. Θ ist der Winkel zwischen der Beobachtungsrichtung und dem
Polarisationsvektor der einfallenden Strahlung. ρn ist der Polarisationsgrad der
Ramanlinie und ist definiert als
ρn =
3γ 2n
45an2 + 4 γ 2n
.
(2.42)
Aus ihm können Informationen über den Polarisierbarkeitstensor gewonnen werden.
Das Intensitätsverhältnis der Stokes- und der Anti-Stokes-Linien (Übergänge), sowie
das Verhältnis der Streuquerschnitte, wird im wesentlichen durch die Besetzung der
Energieniveaus (Gl. 2.36 und 2.37) bestimmt und ist damit abhängig von der Temperatur
[SCH 95]
:
~
hcν n
4
⎛~
IS
ν0 − ~
νn ⎞
(dσ n dΩ) S
=
= ⎜~
⎟ e kT .
I AS
νn ⎠
(dσ n dΩ) AS
⎝ ν0 + ~
(2.43)
Soll aus dieser Gleichung die Temperatur bestimmt werden, so muß berücksichtigt
werden, daß in vielen Fällen der spektrale Abstand zwischen der Stokes- und der AntiStokes-Linie groß ist und dann die spektrale Empfindlichkeit des Detektorsystems
Berücksichtigung finden muß.
Der Einfluß der Flüssigphase
Die bisherigen Betrachtungen gelten nur für den Fall, daß der Brechungsindex des
streuenden Mediums gleich eins ist. Dies ist streng genommen nur im Vakuum möglich,
2. GRUNDLAGEN DER LICHTSTREUUNG
22
kann aber in guter Näherung auch für Gase angenommen werden 4. In Flüssigkeiten ist
der Brechungsindex n deutlich größer als eins, so daß das lokale Feld am Ort des
r
r
streuenden Moleküls D0 höher ist als das Feld der anregenden Strahlung E0 :
r
r
D0 = ε r ε 0 E 0
und
n =
ε rε0 =
ε
(2.44)
mit der absoluten Dielektrizitätskonstante ε, die sich aus der stoffabhängigen
Dielektrizitätszahl εr und der elektrischen Feldkonstante ε0 zusammensetzt. Durch einen
Korrekturfaktor, der zu den Gln. 2.39 und 2.40 multipliziert wird, lassen sich die
bisherigen Betrachtungen auf Flüssigkeiten erweitern
[ECK 66]
[KAI 92]
. Eckhardt und Wagner
schlugen den folgenden Ausdruck für diesen Faktor vor:
ns (ns2 + 2) 2 ⋅ (n02 + 2) 2
L =
,
n0
81
(2.45)
wobei n0 und ns die Brechungsindizes der Flüssigkeit für die einfallende Wellenlänge
bzw. für die gestreute Wellenlänge sind.
Zusätzlich zur Erhöhung des inneren Feldes ändert sich das Raman-Spektrum in der
Flüssigphase. Durch intermolekulare Wechselwirkungen werden die Raman-Linien
verschoben, verbreitert [z.B. MEL 89] und auch deren Intensität beeinflußt [SCH 81]. In einigen
Fällen erscheinen sogar neue Raman-Linien
[WAL 62]
. Auch die Änderung von
thermodynamischen Zuständen kann sich auf ein Raman-Spektrum auswirken. Vehring
et al.
[VEH 92, VEH 95b]
maßen die Temperatur von Wassertropfen im Mikrometerbereich
anhand der Bandendeformation der OH-Schwingung des Wassers.
Der Rotations-Raman-Effekt
Der prinzipielle Formalismus des Rotations-Raman-Effekts und des SchwingungsRaman-Effekts sind sich sehr ähnlich und soll deshalb nicht nochmal wie oben
geschehen hergeleitet werden. Vielmehr werden einige Fakten zusammengestellt, die im
weiteren Verlauf der Arbeit wichtig sind. Der Einfachheit halber soll hier nur der lineare
4
Als Beispiel sei der Brechungsindex von Luft angegeben (15°C, 1 bar, λ im sichtbaren Spektrum)
[LID 92]
: nLuft = 1.00028.
DIE RAMAN-STREUUNG
23
Rotator betrachtet werden, wozu auch das Stickstoff- und das Sauerstoffmolekül gezählt
werden.
Die Rotationsterme berechnen sich nach [HER 91]
Fv ( J ) =
E rot , v
= Bv J ( J + 1) − Dv J 2 ( J + 1) 2 ,
hc
(2.46)
wobei J = 0, 1, 2, ... die Rotationsquantenzahl ist und Bv und Dv Rotationskonstanten
sind, die von einer Schwingung v abhängen. Eine strenge Auswahlregel für Übergänge
zwischen Rotationszuständen existiert wegen der Zentrifugalverzerrung des Moleküls
nicht. Rotationsübergänge mit der gleichen Änderung der Rotationsquantenzahl ∆J faßt
man in sogenannten Zweigen zusammen und bezeichnet sie wie folgt:
∆J
...
-2
-1
0
1
2
...
Zweig ...
O
P
Q
R
S
...
(2.47)
Bei dem Fall ∆J = 0 (Q-Zweig) handelt es sich um einen reinen Schwingungsübergang.
Die Besetzung der Rotationsniveaus ergibt sich nach der Boltzmann-Statistik unter
der Voraussetzung, daß sich alle Moleküle im Schwingungsgrundzustand v = 0 befinden
zu [LEI 84]
nJ
NJ
=
=
N
g J (2 J + 1)
∑ gJ (2 J + 1) e − F ( J )hc kT
v
− Fv ( J )hc
e kT
.
(2.48)
J
Der Faktor (2J+1) berücksichtigt die Entartung der Rotationsquantenzahl J durch die
raumquantisierten magnetischen Quantenzahlen MJ = J, J-1, ... , -J. gJ ist das statistische
Gewicht des Kernspins. Für heteronukleare zweiatomige Moleküle ist es für alle
Rotationsniveaus eins und für homonukleare Moleküle nimmt es für gerade und
ungerade Rotationsquantenzahlen verschiedene Werte an. Aus Tab. 2.1 können die
statistischen Gewichte gJ einiger Moleküle entnommen werden. Man sieht, daß sich für
das Sauerstoffmolekül (16O2) nur Niveaus mit ungerader Rotationsquantenzahl ergeben
und
für
das
Stickstoffmolekül
(14N2)
die
Rotationslinien
mit
gerader
2. GRUNDLAGEN DER LICHTSTREUUNG
24
Rotationsquantenzahl doppelt so intensiv wie die der ungeraden Rotationsquantenzahlen
sind (siehe dazu auch die Ramanspektren im Anhang A, S. 151).
Tabelle 2.1: Statistisches Gewicht des Kernspins gJ für einige Moleküle [LEI 84, LON 77].
gJ
Molekül
Lineare Moleküle mit
gerades J
ungerades J
1
1
unterschiedlichen Kernen, z.B.
CO, NO, CH, CN, NH, OH
16
O2, 18O2
0
1
14
N2, D2
6
3
H2, T2, 19F2, C2H2
1
3
35
Cl2
3
5
CO2
1
0
Abweichungen von den Näherungen
Bei dem bisher Dargestellten sind einige Näherungen gemacht worden. Im Folgenden
sollen diese, deren Abweichungen und einige Spezialfälle diskutiert werden:
1. Das induzierte Dipolmoment wurde in Gl. 2.9 linear proportional zum elektrischen
Feld dargestellt. Für sehr hohe anregende Felder, wie sie mit Lasern leicht erreicht
werden können, genügt diese lineare Näherung nicht mehr:
DIE RAMAN-STREUUNG
r
r
pind = α E +
25
1
2
r
βE 2 +
r
1
γE 3
6
+ ... .
(2.49)
Neben dem Polarisierbarkeitstensor α treten hier noch der Hyperpolarisierbarkeitstensor β und der zweite Hyperpolarisierbarkeitstensor γ auf. Mit Hilfe der nichtlinearen Terme werden die nichtlinearen Raman-Effekte, wie z.B. die stimulierte
Raman-Streuung (SRS; manchmal auch induzierte Raman-Streuung genannt), die
kohärente anti-Stokes Raman-Spektroskopie (CARS) und der Hyper-Raman-Effekt,
erklärt.
Die
Größenordnung
der
Polarisierbarkeitstensoren
ist
ungefähr
α : β : γ = 1 : 10 −8 : 10 −15 . Der Hyperpolarisierbarkeitstensor β ist nur bei
speziellen Kristallen wichtig, während der zweite Hyperpolarisierbarkeitstensor γ für
die oben erwähnten nichtlinearen Effekte von Bedeutung ist.
2. Die Molekülschwingungen sind nicht rein harmonisch. Die Potentialkurve des
harmonischen Oszillators beschreibt eine Parabel, was eine unendlich große
potentielle Energie bei zunehmenden Atomabständen (bei einem dissoziierenden
Molekül)
zur
Folge
hätte.
Eine
Möglichkeit,
die
Anharmonizität
der
Molekülschwingung zu berücksichtigen, besteht in der Verwendung des MorsePotentials [MOR 29] für die potentielle Energie:
V (q ) = De (1 − e − a ( q − q e ) ) 2 .
Hier
ist
q
der
Abstand
zwischen
(2.50)
zwei
Atomkernen
mit
dem
Gleichgewichtsabstand qe. Für q → ∞ wird V = De, der Dissoziationsenergie. Die
Konstanten a und De sind charakteristisch für den jeweiligen elektronischen Zustand
des Moleküls.
Durch die Anharmonizität werden die Wellenfunktionen und die Termenergien
beeinflußt. Um dies zu berücksichtigen, werden die Termenergien des harmonischen
Oszillators (s. Gl. 2.35) als Potenzreihe von (v + 1/2) entwickelt:
G ( v) = ω e ( v + 21 ) − ω e xe ( v + 21 ) 2 + ω e ye ( v + 21 ) 3 + ... ,
(2.51)
2. GRUNDLAGEN DER LICHTSTREUUNG
26
wobei ωexe, ωeye, ... Anharmonizitätskonstanten sind. Im Unterschied zum
harmonischen
Oszillator
sind
die
energetischen
Abstände
zwischen
den
Termenergien nicht mehr äquidistant. Weiterhin sind die Wellenfunktionen des
anharmonischen Oszillators asymmetrisch.
Eine weitere Folge der Anharmonizität ist die Erweiterung der Auswahlregel für
Schwingungsübergänge (s. Gl. 2.25) auf
∆v = ±1, ±2, ±3, ... .
(2.52)
Schwingungsübergänge mit ∆v > ⏐±1⏐ werden als Oberschwingungen oder Obertöne
bezeichnet.
Das Morse-Potential (Gl. 2.61) läßt sich in der Nähe des Minimums gut als Parabel
annähern, so daß die Annahme einer harmonischen Schwingung für Schwingungsübergänge mit ∆v = ±1, die in der Raman-Spektroskopie bei Raumtemperaturen
überwiegen, gerechtfertigt ist.
3. Der Raman-Effekt wird meistens am Beispiel des zweiatomigen homonuklearen
Moleküls erklärt. Häufig liegen jedoch polyatomige heteronukleare Moleküle vor.
Trotzdem kann die Darstellungsweise zur qualitativen Beschreibung des RamanEffekts beibehalten werden, da die Frequenz von Raman-Linien bestimmter
[BRA 62]
.
Atomgruppierungen weitgehend unabhängig vom übrigen Molekülteil sind
Man spricht daher von charakteristischen Frequenzen oder Gruppenfrequenzen. In
Tab. 2.2 sind die Bereiche typischer Regionen von charakteristischen Frequenzen
einiger organischer Komponenten aufgelistet [SCH 95]. Dort stehen die Kürzel X, Y und
Z für Atome von typischen organischen Molekülen: C, O, N, S und die Halogene.
Tabellen charakteristischer Frequenzen und Wellenzahlen vieler Moleküle finden
sich z.B. bei Brandmüller und Moser
[TOB 71]
.
[BRA 62]
, Schrader
[SCH 95]
, Long
[LON 77]
, Tobin
DIE RAMAN-STREUUNG
27
Tabelle 2.2: Bereiche typischer Regionen von charakteristischen Frequenzen einiger
organischer Komponenten [SCH 95]. Die Kürzel X, Y und Z stehen für Atome
von typischen organischen Molekülen: C, O, N, S und die Halogene.
Organische Komponenten
Wellenzahlbereich / cm1
X−H
Streckschwingung
2500 - 3700
X≡Y Streckschwingung,
X=Y=Z antisym. Streckschwingung
2000 - 2500
X=Y
Streckschwingung
1500 - 2000
X−H
Deformationsschwingung
1000 - 1500
X−Y
Streckschwingung, Atome
der zweiten Periode
600 - 1300
Knickschwingungen,
Streckschwingungen von
Guppen schwerer Atome
250 - 400
Gitterschwingungen von
kristallinen Molekülen
20 - 200
2.1.4 Anwendungen des Raman-Effekts
Aus den Grundlagen des Raman-Effekts sollen nun einige Anwendungen abgeleitet
werden, und zwar die Temperaturbestimmung von Gasen und die Messung von
Konzentrationen.
2. GRUNDLAGEN DER LICHTSTREUUNG
28
Temperaturbestimmung von Gasen
Die Messung der Temperatur mit Hilfe der Raman-Spektroskopie wird durch die
Temperaturabhängigkeit der Besetzungsverteilung der Energieniveaus möglich. Die
Besetzungsverteilung wird durch die Boltzmann-Statistik beschrieben (Gl. 2.36). Bei
Raumtemperatur ist, wie oben bemerkt, für die meisten Gase hauptsächlich der
Vibrationsgrundzustand v = 0 besetzt, dort allerdings über viele Rotationszustände
verteilt. Gl. 2.48 kann daher zur Bestimmung der Gastemperatur herangezogen werden.
Eine Möglichkeit ist die Bestimmung des am stärksten bevölkerten Rotationsniveaus:
J max =
kT
1
−
= 0.5896
2hcB0
2
T
− 0.5 .
B0
(2.53)
Hier wurde statt der Gl. 2.46 die Näherung
F ( J ) = B0 J ( J + 1)
(2.54)
mit der Rotationskonstanten B0 benutzt. Der Konturverlauf der Rotationsflügel und
dessen Halbwertsbreite kann auch zur Temperaturbestimmung genutzt werden
Weiterhin
führt
auch
der
Vergleich
einzelner
[LEI 84]
Rotationslinien
.
zur
Temperaturbestimmung. So läßt sich die Intensität benachbarter Linien eines Flügels
(Stokesscher- oder Anti-Stokesscher Rotationsflügel), aber auch die Intensität von den
Linien beider Flügel vergleichen. Die genaueste Temperaturbestimmung erhält man
jedoch durch Auswertung möglichst vieler Rotationslinien.
Die Intensitäten der Rotationslinien für die Stokesschen und Anti-Stokesschen
Rotationsflügel ergeben sich in Abhängigkeit zur Ausgangs-Rotationsquantenzahl J zu
[LEI 84]
( J + 1)( J + 2) −
IS ( J ) = const. ( ~
ν0 − ~
νn ) 4 ⋅ I0 ⋅ N ⋅ g J ⋅
⋅e
(2 J + 3)
J ( J − 1) −
I AS ( J ) = const. ( ~
ν0 + ~
ν n ) 4 ⋅ I0 ⋅ N ⋅ g J ⋅
⋅e
(2 J − 1)
Diese Gleichungen können wie folgt umgeformt werden:
F ( J ) hc
kT
F ( J ) hc
kT
.
(2.55)
(2.56)
DIE RAMAN-STREUUNG
29
J ( J + 1) ⋅
⎡
⎤ ⎫⎪
I S ( J ) ⋅ (2 J + 3)
1
k ⎧⎪
=
⋅ ⎨− ln ⎢
⎥ ⎬ (2.57)
3 )]4 ⎪
T
hcB ⎪
Const
.
⋅
g
⋅
(
J
+
1
)(
J
+
2
)
⋅
[
−
4
B
(
J
+
ν
⎢
⎥⎦ ⎭
J
0
0
2
⎣
⎩
J ( J + 1) ⋅
⎡
⎤ ⎫⎪
I AS ( J ) ⋅ (2 J − 1)
1
k ⎧⎪
=
⋅ ⎨− ln ⎢
⎥⎬ .
1 )]4 ⎪
T
hcB ⎪
Const
.
⋅
g
⋅
J
(
J
−
1
)
⋅
[
+
4
B
(
J
−
ν
⎢
⎥⎦ ⎭
J
0
0
2
⎣
⎩
(2.58)
Die in den Gln. 2.55 bis 2.58 unbedeutenden konstanten Anteile werden in den
sind gemäß
Konstanten const. bzw. Const. zusammengefaßt. Die Wellenzahlen ~ν
0,n
Gl. 2.14 definiert. Trägt man die rechte Seite der Gln. 2.57 und 2.58 gegen J(J+1) auf,
so ergibt sich eine Gerade, deren Steigung umgekehrt proportional zur Temperatur ist.
Die Intensitäten der Rotationslinien sind bei einem reinen Rotationsspektrum am
größten. Hat man jedoch mehr als eine Gasspezies, so überlagern sich deren
Rotationslinien. Außerdem liegen die Rotationslinien spektral sehr dicht an der
Anregungswellenlänge, sodaß eine effektive Unterdrückung des elastisch gestreuten
Lichts nötig wird. Diese Nachteile werden durch Messen des Rotations-Schwingungsspektrums umgangen. Die Gln. 2.55 bis 2.58 können trotzdem benutzt werden, da alle
Faktoren des Schwingungsübergangs mit in die Konstanten genommen werden können.
Messung von Konzentrationen
Für die gemessene Intensität einer Raman-Linie muß Gl 2.38 um einige Faktoren
ergänzt werden, die für die Praxis vorteilhaft sind:
IA =
∂σ A
⋅ c A ⋅ N A ⋅ V ⋅ Ω obs ⋅ F −1 ⋅ C ⋅ I0 ,
∂Ω
(2.59)
wobei Ωobs der Raumwinkel ist, der experimentell zugänglich ist und C ein Faktor, der
die Effizienz des Detektionssystems berücksichtigt. Die Anzahl der Streuteilchen pro
Volumenelement wird ersetzt durch die molare Dichte cA (Konzentration) der
Streuteilchenspezies A bezogen auf die Gesamtteilchenzahl pro mol (NA, AvogadroKonstante) aus dem Beobachtungsvolumen V. Die Fläche F sei die Projektion der
Detektoröffnung (i.a. die Fläche des Monochromatorspaltes) auf das Untersuchungs-
2. GRUNDLAGEN DER LICHTSTREUUNG
30
volumen, durch welches das zu messende Streulicht fällt. Gl. 2.59 gilt für eine gemittelte
Intensität I0 der anregenden Strahlung im Beobachtungsvolumen V. Weiterhin wird wie
bei Gl. 2.38 angenommen, daß der differentielle Streuquerschnitt im Beobachtungsraumwinkel Ωobs konstant ist.
In manchen Fällen wird die „Stärke“ einer Raman-Linie nicht als Intensität
(Strahlungsflußdichte; SI-Einheit W/m2) angegeben, sondern als Strahlungsfluß
(Strahlungsleistung, gestreute Leistung; SI-Einheit W)
P bzw. Φ = I ⋅ F .
(2.60)
Da die Intensität der Anregungsstrahlung I0, das Beobachtungsvolumen, die
durchstrahlte Fläche, der Beobachtungsraumwinkel und der Effizienzfaktor im
allgemeinen während eines Experiments konstant gehalten werden, ist die Intensität
einer gemessenen Ramanlinie linear proportional zur Konzentration der Streuteilchen.
Daher ist die lineare Raman-Spektroskopie inzwischen ein etabliertes Verfahren zur
Ermittlung von Stoffmengenkonzentrationen.
Im allgemeinen wird für Konzentrationsmessungen das Intensitätsverhältnis von zwei
Raman-Linien unterschiedlicher Spezies gemessen. In diesem Fall kürzen sich alle
experimentell bedingten Faktoren aus Gl. 2.59 heraus. Das Intensitätsverhältnis ist dann
nur noch von den Konzentrationen der Spezies A und B und den differentiellen
molekularen Streuquerschnitten abhängig:
IA
∂σ A ∂Ω cA
=
.
∂σ B ∂Ω cB
IB
(2.61)
Gl. 2.61 gilt nur für homogene Gemische. Die Bestimmung der Konzentration von
Mikropartikeln, die aus einem inhomogenen Gemisch bestehen, wird in Kap. 3
behandelt. Das Verhältnis der Streuquerschnitte ist nicht immer bekannt. Daher erfolgt
die Zuordnung des Verhältnisses der Ramanstreuintensitäten zum Verhältnis der
Konzentrationen über Kalibrierungsmessungen, bei denen bekannte Konzentrationen der
Spezies eingestellt werden:
DIE RAMAN-STREUUNG
31
⎛ IA ⎞
∂σ A ∂Ω ⎛ cA ⎞
.
=
⎜ ⎟
⎜ ⎟
∂σ B ∂Ω ⎝ cB ⎠ kal
⎝ I B ⎠ kal
(2.63)
Dabei müssen die Temperatur und der Druck für die Kalibrierungsmessungen ebenso
eingestellt werden, wie für die zu untersuchende Probe. Will man cA bei bekannter
Konzentration cB bestimmen, setzt man Gl. 2.63 in Gl. 2.61 ein und formt nach cA um:
cA = cB ⋅
⎛c ⎞
IA ⎛ IB ⎞
⋅⎜ ⎟ ⋅⎜ A ⎟
.
I B ⎝ I A ⎠ kal ⎝ cB ⎠ kal
(2.64)
Für viele Gasuntersuchungen wird für die Spezies B Stickstoff oder Sauerstoff als
interner Standard genommen. Bei Flüssigkeiten können Salze hinzugefügt werden, auf
die
eine
zu
untersuchende
Probe
bezogen
werden
kann.
Wechselwirkungen zwischen den Spezies berücksichtigt werden.
Dabei
müssen
2. GRUNDLAGEN DER LICHTSTREUUNG
32
2.2 Die Mie-Streuung
Die elastische Lichtstreuung an sphärischen Partikeln, deren Durchmesser größer
oder vergleichbar mit der Wellenlänge des Lichtes ist, wird Mie-Streuung genannt. Die
grundlegenden theoretischen Arbeiten zu diesem Streulichteffekt wurde 1908 von dem
deutschen Physiker Gustav Adolf Ludwig Mie
[LOR 90]
[MIE 08]
und 1890 von Ludvig Lorenz
veröffentlicht. Daher wird die Theorie dieses Effekts nach diesen beiden Autoren
benannt: Lorenz-Mie-Theorie. Eine wichtige Erscheinung des Mie-Effekts ist, daß mit
wachsendem Durchmesser der Partikel die Streuintensität in Vorwärtsrichtung stärker
zunimmt, als in Rückwärtsrichtung.
Die Lichtstreuung an Partikeln, die kleiner sind als die Wellenlänge des Lichtes und
deren mittlere Abstände groß gegen diese sind, wird Rayleigh-Streuung genannt. Die
Rayleigh-Streuung ist der Grenzfall zur Mie-Streuung für kleine Partikel. Die
Winkelverteilung der Rayleigh-Streuung ist gleich der Abstrahlcharakteristik eines
Dipols: in Vorwärts- und Rückwärtsrichtung sind die gestreuten Intensitäten gleich groß.
Typische Streupartikel sind Moleküle. Während die Rayleigh-Streuung die Blaufärbung
des Himmels verursacht, ist die Mie-Streuung für die Weißfärbung von z.B. Wolken
verantwortlich.
In den folgenden Monographien werden die Lichtstreuung an Partikeln ausführlich
behandelt: Bohren und Huffmann
[BOH 83]
, Kerker
[KER 69]
, van de Hulst
[HUL 57]
und
Bayvel und Jones [BAY 81].
Im Folgenden soll die Theorie der elastischen Lichtstreuung an Partikeln nur in
soweit betrachtet werden, als daß der mathematische Weg zu deren Beschreibung
deutlich wird. Für eine eingehendere Betrachtung sei auf das Werk von Bohren und
Huffmann
[BOH 83]
verwiesen, das im wesentlichen als Vorlage diente. Ausgehend von
den Maxwellschen Gleichungen wird auf die elastische Streuung an Kugeln
eingegangen.
DIE MIE-STREUUNG
33
Die Maxwellschen Gleichungen
Die Beschreibung des Lichts als elektromagnetische Welle wurde von James Clerk
Maxwell erstmalig durchgeführt. Zahllose Monographien über die Elektrodynamik
behandeln dieses Problem, wie z.B. die von Stratton [STR 41] und Jackson [JAC 83].
Die elektrischen und magnetischen Felder des Lichts sind zeit- und ortsabhängig
durch die Maxwellschen Gleichungen verbunden. Diese lauten für ein lineares, isotropes
und homogenes Medium:
r
r
∂ E
∇ × H − ε oε r
∂t
=
r
σE ,
(2.65)
r
r
∂ H
∇ × E + µ 0µ
∂t
=
0 ,
(2.66)
r
∇⋅ E
=
0 ,
(2.67)
r
∇⋅ H
=
0 .
(2.68)
r
r
Hier sind E die elektrische und H die magnetische Feldstärke, t die Zeit, σ die
elektrische Leitfähigkeit, ε0 die elektrische und µ0 die magnetische Feldkonstante. εr ist
die (relative) Dielektrizitätszahl und µr die (relative) Permeabilitätszahl des Mediums1.
Vorausgesetzt wird, daß die Ladungsdichte ρ = 0 ist, mit anderen Worten, das Medium
r
sei elektrisch neutral (anderenfalls würde aus Gl. 2.67: ∇ ⋅ E = ρ ε ).
r
Aus diesem Gleichungssystem (Gln. 2.65 bis 2.68) kann einer der Vektoren E und
r
H eliminiert werden. Durch Bilden der Rotation von Gl. 2.66, Benutzen der geeigneten
Vektoroperation
und
Einsetzen
von
Gl. 2.65 und Gl. 2.67 erhält man die
Wellengleichung für das elektrische Feld (in vektorieller Form):
1
Für Vakuum gilt εr = µr = 1. ε0 und εr können zur (absoluten) Dielektrizitätskonstante ε = ε0εr
zusammengefaßt werden, genauso wie µ0 und µr zur (absoluten) Permeabilität µ = µ0µr zusammengefaßt
werden können. εr und µr sind dimensionslose Größen. Weiterhin sind ε und µ Materialeigenschaften,
aus denen sich die Ausbreitungsgeschwindigkeit c =
elektromagnetischer Wellen ableiten lassen.
εµ und der Brechungsindex m = ε r µ r
2. GRUNDLAGEN DER LICHTSTREUUNG
34
r
r
∇ 2 E + m2 k02 E
=
0 .
(2.69)
r
In entsprechender Weise kann E eliminiert werden und man erhält die Wellengleichung
für das magnetische Feld:
r
r
∇ 2 H + m2 k02 H
=
0 .
(2.70)
Hierbei ist
m =
ε − i εσω
(2.71)
0
der komplexe Brechungsindex und
k0 = ω c0 = ω ε 0µ 0
(2.72)
die Wellenzahl (k0 = 2πν/c0) im Vakuum. Weiterhin wird vorausgesetzt, daß die
magnetische Permeabilität µ ungefähr 1 ist, was im Wellenlängenbereich des sichtbaren
Lichts für die meisten Medien eine vernünftige Annahme ist.
Eine Lösung der Wellengleichungen und damit auch der Maxwellschen Gleichungen
ist der harmonische Ansatz für die elektrischen und magnetischen Felder
r r
r
r
E = E0 exp[i( k ⋅ r − ωt )]
,
(2.73)
r r
r
r
H = H 0 exp[i( k ⋅ r − ωt )] ,
(2.74)
r
r
mit der Kreisfrequenz ω und dem Wellenvektor k = ω c ⋅ n , in dessen Richtung der
r
Einheitsvektor n zeigt. c ist die Lichtgeschwindigkeit im Medium.
Man kann zeigen, daß sich die Wellengleichungen 2.69 und 2.70 auch in der Form
∇2ψ + k 2ψ
=
0
(2.75)
schreiben lassen, wobei ψ eine skalare Größe und k = mk0 ist. Wenn ψ eine Lösung der
Wellengleichung ist, dann lassen sich auch zwei linear unabhängige Lösungen der Form
DIE MIE-STREUUNG
35
r
r
M = ∇ × (c ψ )
r
N =
1
k
und
(2.76)
r
∇×M
(2.77)
r
r
r
r
finden, da ∇ ⋅ M = ∇ ⋅ N = 0 (wegen div rot = 0) ist und somit M und N ebenfalls die
r
Wellengleichung befriedigt (vergleiche dazu auch Gln. 2.69 und 2.70). c ist hier ein
noch beliebiger, konstanter Vektor.
Wegen der Linearität der Maxwellgleichungen können das elektrische und das
magnetische
Feld
in
einem
Medium
als
eine
Summe
von
Einzelfeldern
(Superpositionsprinzip) geschrieben werden,
r
E
=
E0
r
r
∑ ( Bn Nn + An Mn )
und
(2.78)
n
r
H
=
k
E0
iµ 0 ω
∑
r
r
( An N n + Bn Mn ) ,
(2.79)
n
die wiederum die Wellengleichungen erfüllen. Diese Entwicklung wird auch
Multipolentwicklung genannt, wobei An und Bn die Entwicklungskoeffizienten sind.
Anwendung auf sphärische Partikel
Die Multipolentwicklung der elektrischen und magnetischen Felder läßt sich auf
beliebige Geometrien anwenden. Für die Lichtstreuung an sphärischen Partikeln bietet
es sich an, Polarkoordinaten mit den Ortskoordinaten r, θ und φ einzuführen. Die skalare
Größe ψ läßt sich dann wie folgt zu einem Produkt separieren, wobei jeder Faktor
lediglich von einer Ortskoordinate abhängt:
ψ ( r , θ, φ ) = F ( r ) G (θ ) H ( φ ) .
(2.80)
Für jeden Faktor läßt sich nun eine Lösung der skalaren Wellengleichung (s. Gl. 2.75) in
Polarkoordinaten finden, so daß man drei Differentialgleichungen erhält. Aus den
Lösungen der Differentialgleichungen erhält man je einen Ausdruck für jeden Faktor, so
daß sich die Lösung der skalaren Wellengleichung wie folgt ergibt [BOH 83, STR 41]:
2. GRUNDLAGEN DER LICHTSTREUUNG
36
ψ e ln (r, θ, φ) = zn (ρ) Pnl (cos θ)
o
cos(lφ)
,
sin(lφ)
(2.81)
wobei Pnl die Legendre-Polynome vom Grad n und der Ordnung l sind und zn ist eine
sphärische Besselfunktion der ersten oder zweiten Art oder eine Linearkombination der
beiden. Mit e und o (even=gerade und odd=ungerade) sind zwei Lösungen der φabhängigen
Differentialgleichung
gemeint.
Damit
ergeben
sich
die
beiden
Multipolfelder (s. Gln. 2.76 und 77) zu:
r
M e ln
⎛
⎜
⎜
⎜
= ⎜
⎜
⎜
⎜
⎜
⎝
r
N e ln
⎛
⎜
⎜
⎜
⎜
= ⎜
⎜
⎜
⎜
⎜
⎝
o
o
⎞
⎟
0
⎟
⎟
φ
−
sin
l
l
⎟
Pnl (cos θ) zn (ρ)
cos lφ ⎟
sin θ
⎟
cos lφ
dPnl (cos θ)
⎟
−
zn (ρ)
⎟
dθ
sin lφ
⎠
n(n + 1) Pnl (cos θ)
dPnl (cos θ)
dθ
Pnl (cos θ)
sin θ
zn (ρ) cos lφ
sin lφ
ρ
cos lφ
1 d
[ρzn (ρ)]
sin lφ
ρ dρ
− sin lφ
1 d
[ρzn (ρ)]
ρ dρ
cos lφ
und
⎞
⎟
⎟
⎟
⎟
⎟,
⎟
⎟
⎟
⎟
⎠
(2.82)
(2.83)
die auch Vektorkugelfunktionen genannt werden. Mit ihnen lassen sich das elektrische
und magnetische Feld (Gln. 2.78 und 2.79) in Polarkoordinaten darstellen.
Streuung an sphärischen Partikeln
Fällt eine ebene elektromagnetische Welle auf eine Kugel, so werden die einfallenden
elektrischen und magnetischen Felder an ihr gestreut. Da der mathematische
Formalismus für die Streuung der magnetischen Felder analog zu dem der elektrischen
Felder ist, wird im Folgenden nur der Streuvorgang der elektrischen Felder betrachtet.
DIE MIE-STREUUNG
37
Bei dem entstehenden Streuprozeß unterscheidet man folgende Felder, die nach
Vektorkugelfunktionen entwickelt werden [BOH 83]:
1. Das einfallende Feld (Index inc = incident)
∞
r
Einc = E0 ∑ i n
r (inc )
r (inc )
2n + 1
+ iNen
( Mon
) ,
n(n + 1)
n =1
(2.84)
welches als linear polarisiert vorausgesetzt wird;
2. das gestreute Feld (Index sca = scattered)
∞
r
Esca = E0 ∑ i n
n =1
r ( sca )
r ( sca )
2n + 1
− bn Mon
(ian Nen
)
n(n + 1)
(2.85)
der Kugel und
3. das transmittierte Feld (Index t = transmitted)
∞
r
Et = E0 ∑ i n
n =1
r (t )
r (t )
2n + 1
+ idn Nen
(cn Mon
)
n(n + 1)
(2.86)
im Inneren der Kugel. Hier bedeutet E0 die Amplitude der einfallenden Welle, die sich
in z-Richtung ausbreitet. an, bn, cn und dn sind die Entwicklungskoeffizienten der
Multipolfelder (Mie-Koeffizienten):
an =
mψ n ( mx )ψ ′n ( x ) − ψ n ( x )ψ ′n ( mx )
mψ n ( mx )ξ ′n ( x ) − ξ n ( x )ψ ′n ( mx )
,
(2.87)
bn =
ψ n ( mx )ψ ′n ( x ) − mψ n ( x )ψ ′n ( mx )
ψ n ( mx )ξ ′n ( x ) − mξ n ( x )ψ ′n ( mx )
,
(2.88)
cn =
− im
ψ n ( mx )ξ ′n ( x ) − mξ n ( x )ψ ′n ( mx )
und
(2.89)
dn =
− im
mψ n ( mx )ξ ′n ( x ) − ξ n ( x )ψ ′n ( mx )
,
(2.90)
wobei m der Brechungsindex des Tropfenmediums und
2. GRUNDLAGEN DER LICHTSTREUUNG
38
x = k0a =
2πa
λ
(2.91)
der Größen- oder Mie-Parameter einer Kugel mit dem Radius a ist. x ist daher das
Verhältnis des Kugelumfangs zur einfallenden Wellenlänge λ. Die Funktionen ψn und ξn
sind Riccati-Besselfunktionen.
Im Außenraum der Kugel (r > a) überlagern sich das einfallende und das gestreute
Feld. An der Phasengrenzfläche vom Umgebungsmedium zur Kugel (r = a) müssen die
Grenzwertbedingungen erfüllt werden, d.h., die Tangentialkomponenten der Felder
müssen dort stetig sein [STR 41, JAC 83]. Innerhalb der Kugel (r ≤ a) wird das elektrische
r
Feld durch Et mit deren Komponenten
Er = E0
∞
cos φ
k 2r 2
∑
i n −1 (2n + 1)dn ψ n ( kr )π n sin(θ) ,
(2.92)
n =1
∞
dP (cos θ)
P (cos θ) ⎤
cos φ
2n + 1 ⎡
+ icn ψ n ( kr ) n
i n −1
dn ψ ′n ( kr ) n
, (2.93)
Eθ = E0
⎢
sin θ ⎥⎦
kr n =1
n(n + 1) ⎣
dθ
∑
∞
P (cos θ)
dP (cos θ) ⎤
sin φ
2n + 1 ⎡
i n −1
dn ψ ′n ( kr ) n
+ icn ψ n ( kr ) n
Eφ = − E0
⎥⎦
⎢
sin θ
kr n =1
n(n + 1) ⎣
dθ
∑
(2.94)
beschrieben. Die Riccati-Besselfunktionen werden als Funktion von der Wellenzahl k
und der radialen Komponente r dargestellt.
Strukturresonanzen
Bei bestimmten Mie-Parametern kann das transmittierte Feld innerhalb eines
Partikels sprunghaft um mehrere Größenordnungen ansteigen. Der Grund sind
sogenannte Strukturresonanzen, die auch „Morphology-dependent resonances“ (MDR)
[OWE 82]
oder „Whispering gallery modes“ (WGM)
Zusammenfassung
der
experimentellen
und
[GAR 61]
genannt werden. Eine gute
theoretischen
Arbeiten
über
DIE MIE-STREUUNG
Strukturresonanzen kann man bei Hill und Benner
39
[HIL 88]
sowie Hill und Chang
[HIL 92]
nachlesen.
Man kann sich die Strukturresonanzen als Oberflächenwellen vorstellen, die sich
innerhalb der Partikel durch Totalreflexion ausbreiten und in der richtigen Phase an der
Ausgangsposition ankommen. Durch ein- oder mehrfache Überlagerung und
konstruktive Interferenz wird das transmittierte Feld drastisch erhöht. Nach der bisher
gängigen Überzeugung geschieht die Einkopplung des elektromagnetischen Feldes in
die Partikel durch Beugung. Neuere Erkenntnisse deuten darauf hin, daß das
elektromagnetische Feld in die Partikel eintunnelt [WIE 98]. Nur so ist zu verstehen, wie es
zur Totalreflexion innerhalb der Partikel kommen kann. Durch Beugung wird auch ein
Teil des elektromagnetischen Feldes ausgekoppelt; anderenfalls würde die Resonanz
nicht sichtbar oder meßbar sein. Tritt eine Resonanz auf, so erhöht sich auch das
gestreute Feld. Ein Beispiel für elastische Lichtstreuung an der Tropfenkette mit
Resonanzen ist in Bild 2.3 zu sehen.
Mathematisch lassen sich die Strukturresonanzen als Pole der Mie-Koeffizienten
(Gln. 2.87 bis 2.90) erklären. Wird der Nenner eines Mie-Koeffizienten Null, so erhält
man eine Nullstelle im Imaginärteil und ein Maximum im Realteil. Der Realteil nimmt
dann den Wert 1 an, wenn der Imaginärteil des komplexen Brechungsindexes Null ist,
d.h., das Partikel ist nicht absorbierend. Die Mie-Koeffizienten stellen die Amplituden
von Partialwellen (einzelner Multipole) dar, sodaß im Resonanzfall die Amplitude
ansteigt und damit das Feld erhöht wird. Tritt Absorption in den Partikeln auf (mit
anderen Worten, der Imaginärteil des Brechungsindex wird größer als Null), so wird die
Oberflächenwelle gedämpft und die Amplitude der Resonanz kleiner [z.B. LAN 96a, TU 98].
2. GRUNDLAGEN DER LICHTSTREUUNG
40
Frequenz / Hz
287956
274869
262563
126
128
130
132
250981
240070
229783
220075
210907
202240
134
136
138
140
142
144
Intensität / willk. Einheiten
309190
Mieparameter x
Bild 2.3: Elastische Lichtstreuung (TM) an der Tropfenkette als Funktion des
Mieparameters und der Tropfenerzeugungsfrequenz. Das Streuspektrum
wird 5 mm unterhalb des Tropfenkettengenerators an Tropfen gemessen,
die zu gleichen Teilen aus Wasser und Ethanol bestehen
[LEX 98]
. Jede
Spitze in diesem Spektrum stammt von einer Strukturresonanz.
Die Resonanzen werden nach ihren Koeffizienten (Gln. 2.87 bis 2.90) bezeichnet. Da
die Nenner von an und dn sowie von bn und cn gleich sind, treten die Resonanzen des
gestreuten (Gl. 2.85) und des transmittierten (Gl. 2.86) Feldes an derselben Position auf.
Daher werden Resonanzen nur nach den Koeffizienten an oder bn bezeichnet. n bedeutet
dabei die Modennummer, die die Anzahl der Maxima zwischen 0° und 180° in der
Winkelabhängigkeit der Resonanzmode bestimmt. Zusätzlich können für einen
Koeffizienten mit einer Modennummer mehrere Resonanzpositionen auftreten. Daher
wird zusätzlich ein zweiter Index eingeführt, der die Resonanzen gleicher Modenzahlen
entsprechend der Größe des Resonanz-Mie-Parameters (radiale Position innerhalb der
Partikel) durchnumeriert [CON 84], mit anderen Worten, er gibt die Anzahl der Maxima in
der radialen Intensitätsverteilung an. Dieser Index wird als Ordnung der Resonanz
DIE MIE-STREUUNG
41
bezeichnet. Eine Eigenschaft der Resonanzordnung ist die Abnahme der Intensität einer
Resonanz mit zunehmender Ordnung. Außerdem wird der radiale Bereich, in dem die
Resonanzen auftreten, mit zunehmender Ordnung größer. Für ein Partikel mit dem
Brechungsindex m = 1.5 erhöht eine Resonanz 1. Ordnung das transmittierte Feld also
nur sehr nah an der Oberfläche (etwa 0.85a ≤ r ≤ a), während eine Resonanz 3. Ordnung
etwa den Bereich 0.7a ≤ r ≤ a einnimmt. Innerhalb der Partikel (0 ≤ r ≤ 0.7a) befindet
sich das wesentlich schwächere nichtresonante Feld (vergleiche dazu Bild 2.4).
8
2x10
1
Resonanz a 70
x = 51.799860733753
8
winkelgemittelte elektrische Energiedichte
1x10
0
4
3x10
2
Resonanz a 65
x = 52.3396621497
4
2x10
4
1x10
0
3
60
Resonanz a 60
x = 52.08358324
40
20
0
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Radius r / a
Bild 2.4: Winkelgemittelte elektrische Energiedichte des transmittierten Feldes in
einem Mikropartikel mit m = 1.5 als Funktion der radialen Komponente
für die ersten drei Ordnungen.
2. GRUNDLAGEN DER LICHTSTREUUNG
42
Die Mie-Koeffizienten a und b hängen von der Polarisation des einfallenden Feldes
ab. Resonanzen im Koeffizienten a liegen in der Polarisationsebene, während die dazu
orthogonal liegenden Resonanzen im Koeffizienten b senkrecht zur Polarisationsebene
des einfallenden Feldes liegen. Bezeichnet werden die Resonanzen des Koeffizienten a
als elektrisch oder transversal magnetisch (TM) und die des Koeffizienten b als
magnetisch oder transversal elektrisch (TE).
Qualitativ läßt sich weiter sagen, daß Resonanzen mit ansteigendem Mie-Parameter
schmaler werden und häufiger auftreten. Auch die Ordnung einer Resonanz wirkt sich
auf die Breite der Resonanz aus. Mit größer werdender Ordnung bei gleichem MieParameter werden die Resonanzen breiter. Eine sehr brauchbare Abschätzung zur
Ermittlung des Mie-Parameters eines Partikels lieferte Chylek
[CHY 90]
: Der Abstand
zweier Resonanzen gleicher Ordnung l mit aufeinanderfolgenden Modennummern n
ergibt sich aus
x nl +1
−
x nl
=
x arctan ( mx / n )2 − 1
.
n
( mx / n ) 2 − 1
(2.95)
Diese Beziehung gilt für x >> 1, n >> 1, x/n ≈ 1, mx > n und x − n >> 1/2 sowie für TEund TM-Moden. Vernachlässigt man die schwache Abhängigkeit des Mie-Parameters x
und der Modennummer n auf den Abstand zweier Resonanzen, vereinfacht sich
„Chyleks Beziehung“ (Gl. 2.95), indem x/n = 1 gesetzt wird.
Eine Reihe von Forschern beschäftigt sich mit der Untersuchung von Mikropartikeln
durch die Analyse von Strukturresonanzen. Das Auftreten von Strukturresonanzen im
elastischen Streulicht wurde zuerst von Ashkin und Dziedzic [ASH 77] beobachtet und von
Chylek et al.
[CHY 76]
berechnet. Im Folgenden werden nur einige wenige ausgewählte
Literaturstellen angegeben, die jeweils selbst einen guten Literaturüberblick verschaffen.
Die präzise Bestimmung von Größe und Brechungsindex wurden von Ray et al. [RAY 91] ,
Huckaby et al.
[HUC 94]
und Popp et al.
[POP 98]
für einzelne homogene Mikropartikel und
für geschichtete Mikropartikel von Ray et al.
[RAY 95]
und Kaiser et al.
[KAI 95, KAI 96b]
bestimmt. Ähnnliche Untersuchungen an der Tropfenkette wurden von Lin et al. [LIN 90b],
Eversole et al. [EVE 93, EVE 95] und Devarakonda et al. [DEV 98] durchgeführt.
DIE MIE-STREUUNG
43
Wesentlich einfacher als die oben beschriebene Theorie der Ausbreitung
elektromagnetischer Wellen in Mikroprartikeln ist die Theorie der geometrischen Optik.
Mit ihr wird die Ausbreitung des Lichts durch „Strahlen“ beschrieben, sodaß die
Gesetze der Geometrie angewendet werden können. Für die geometrische Optik im
allgemeinen sei als Beispiel auf das Werk von Born und Wolf
[BOR 93]
und auf die
Beschreibung von Strukturresonanzen mit Hilfe der geometrischen Optik auf Roll et al.
[ROL 98]
verwiesen. Roll konnte zeigen, daß die Eindringtiefe rres,min von Resonanzen in
Mikropartikeln mit dem Brechungsindex m verknüpft ist (vergl. dazu Bild 2.4):
rres,min =
a
.
m
(2.96)
2. GRUNDLAGEN DER LICHTSTREUUNG
44
2.3 Ramanstreuung an Mikropartikeln
Einführung
Zur Beschreibung der Raman-Streuung an Mikropartikeln müssen einige erarbeitete
Ergebnisse der beiden vorhergehenden Unterkapitel kombiniert werden. Wie aus
Gl. 2.38 (S. 20) hervorgeht, ist die spontane Raman-Streuung linear proportional zur
einfallenden Strahlungsflußdichte (Gl. 2.31, S.17) des anregenden Laserlichts. In
Kapitel 2.2 wird gezeigt, daß die Wechselwirkung der einfallenden Strahlung mit
sphärischen Mikropartikeln dazu führt, daß das transmittierte Feld innerhalb der Partikel
stark inhomogen ist (Gln. 2.92 bis 2.94, S.38). Dieses transmittierte Feld regt jedoch die
Raman-Streuung an, sodaß unterschiedliche Bereiche des Partikels verschieden angeregt
werden. Das gleiche gilt für die Fluoreszenz in Mikropartikeln. Besonders signifikant
wird dies, wenn Strukturresonanzen bei der Raman-Streuung
[z.B. THU 84, LET 85, GS 90c]
und
der Fluoreszenz [BEN 80, HIL 84, OWE 82] angeregt werden.
Modellierung
Die Berechnung der Ramanstreuung an Mikropartikeln kann mit einem sogenannten
Dipolmodell gemacht werden, das von Chew und Kerker [CHE 76, KER 78] entwickelt wurde.
Demnach besteht das Partikel aus Dipolen, nämlich den Molekülen, die durch das
transmittierte Feld (siehe Kap. 2.2, S. 32ff) angeregt werden. Jeder Dipol emittiert
darauf Strahlung, die sich abhängig von der Position des Dipols innerhalb des Partikels
ausbreitet. Das von allen Dipolen gestreute Feld, das Dipol- oder Ramanfeld, ist damit
ebenso ortsabhängig, wie das transmittierte Feld. Zur Berechnung des Dipolfeldes
[RAM 88]
wird die Anzahl der Dipole wesentlich geringer als die Anzahl der Moleküle
gehalten, um die Rechenzeit zu begrenzen. Der Formalismus ist ähnlich wie bei der
Berechnung der elastischen Lichtstreuung. Auch hier werden die Felder in einer
Multipolentwicklung dargestellt.
RAMANSTREUUNG AN MIKROPARTIKELN
45
Um den komplizierten Zusammenhang zwischen dem transmittierten Feld und der
Emission der Dipole etwas zu vereinfachen, wird der differentielle Streuquerschnitt
eines Partikels in zwei Faktoren aufgespalten. Ein Faktor berücksichtigt die molekularen
Eigenschaften, wie schon in Kap. 2.1.3 (Gln. 2.39 und 2.40, S. 20) gemacht wurde und
ein zweiter (fP) die Streugeometrie im Partikel [GS 87, GS 91b]:
dσ aP, n
dΩ
=
dσ a, n
dΩ
f P ( x 0 , m0 , x s , m s ) .
(2.97)
Der Faktor fP ist dimensionslos und hängt von den Mie-Parametern der einfallenden
Wellenlänge x0 und der gestreuten Wellenlänge xs sowie den Brechungsindizes zu
beiden Wellenlängen m0 und ms ab. Der erste Faktor entspricht dem Ramanspektrum
einer chemischen Komponente a, wie in einer Küvette zu messen ist.
Geometrische Optik
Die Berechnung des Dipolfeldes mit Hilfe der Multipolentwicklung ist ein sehr
aufwendiges Verfahren, das viel Rechenzeit benötigt. Mit der geometrischen Optik
lassen sich jedoch recht schnell qualitative Ergebnisse erzielen, die die Strahlenverläufe
und die Strahlenverteilung innerhalb eines Partikels veranschaulicht
[GS 90a]
. Wird z.B.
ein Dipol im Bereich des „hot spots“ (vergl. dazu Kap. 2.2) angeregt, emittiert dieser
bevorzugt in Richtung der Rückwärtsstreuung, da ein wesentlicher Teil der Strahlung in
Vorwärtsrichtung auf die Partikeloberfläche trifft und in Rückwärtsrichtung reflektiert
wird.
In letzter Zeit wurden die Modelle der geometrischen Optik für Mikropartikel
weiterentwickelt. Unter Berücksichtigung einiger wellenoptischer Phänomene, wie z.B.
Phasenbeziehungen und Beugungserscheinungen, lassen sich Ergebnisse erzielen, die
denen aus der Berechnung mit Hilfe der Multipolentwicklung sehr nahe kommen.
Beispiele dazu und weitere Literaturhinweise sind bei Velesco et al. [VEL 98] nachzulesen.
2. GRUNDLAGEN DER LICHTSTREUUNG
46
Strukturresonanzen
Nicht nur das von außen auf ein Mikropartikel einfallende Feld kann bei der
elastischen Lichtstreuung (Mie-Streuung) im Inneren der Partikel Strukturresonanzen
anregen, wie schon in Kap. 2.2 (S. 32ff) beschrieben, sondern auch die im Inneren der
Partikel emittierte Strahlung kann zu Strukturresonanzen führen. Die Resonanzen der
elastischen Lichtstreuung werden Eingangs- oder Inputresonanzen, die der inelastischen
Lichtstreuung werden Ausgangs- oder Outputresonanzen genannt. Ausgangsresonanzen
treten bei der Ramanstreuung [z.B. LET 85, GS 90b+c, THU 85, OWE 82], der Fluoreszenz
HIL 84, OWE 81, OWE 82]
und der Laseremission
[z.B. CAM 91, QIA 86, TZE 84]
[z.B. BEN 80,
auf und erhöhen die
spontanen und induzierten Emissionsraten in einer Partikel drastisch. Dabei ist die
Orientierung der Dipole in der Nähe der Partikeloberfläche wichtig, die die relativen
Höhen der Ausgangsresonanzen beeinflußt [LAN 96a].
Wie bei den Eingangsresonanzen treten Ausgangsresonanzen bei bestimmten
Größenparametern (Gl. 2.91, S. 38) auf. Am anschaulichsten verdeutlicht man sich dies,
indem man sich ein Partikel mit festem Durchmesser vorstellt und nur die Wellenlänge
variiert. Dann erscheinen die Ausgangsresonanzen bei bestimmten Wellenlängen, die
einem Größenparameter zugeordnet sind. Praktisch heißt dies, daß z.B. in einem
Ramanspektrum an ganz bestimmten Wellenlängen (bzw. Wellenzahlenverschiebungen)
Intensitätserhöhungen auftreten. Dies wird deutlich beim Betrachten von Bild 2.5, in
dem zwei Ramanspektren der OH-Bande des Wassers gezeigt sind, wobei das eine
Spektrum an der Küvette und das andere Spektrum an der Tropfenkette aufgenommen
wurde. Im Tropfenkettenspektrum sieht man eine Reihe von Resonanzen, die dem
eigentlichen Wasserspektrum überlagert sind. Beim Betrachten der Resonanzen ist eine
wiederkehrende Struktur zu erkennen. Daraus lassen sich Resonanzen gleicher Ordnung
ermitteln, die in etwa gleichen Abständen auftreten. Aus dem Abstand zweier
Resonanzen läßt sich wiederum die Größe der Partikel mit Hilfe der „Chylekschen
Beziehung“ (Gl. 2.95) abschätzen
[CHY 90]
. Allerdings muß erwähnt werden, daß
„Chyleks Beziehung“ streng genommen nur für einen Brechungsindex gilt.
Ausgangsresonanzen gleicher Ordnung erkennt man jedoch bei verschiedenen
Wellenlängen
und
damit
bei
unterschiedlichen
Brechungsindizes,
der
RAMANSTREUUNG AN MIKROPARTIKELN
47
40000
a.)
30000
intensity / a.u.
20000
10000
0
b.)
30000
20000
10000
0
3100
3200
3300
3400
3500
W ellenzahlverschiebung / cm
3600
-1
Bild 2.5: Ramanspektren von der OH-Bande des Wassers: a.) das untere Spektrum
wurde an der Küvette und das obere an der Tropfenkette gemessen; b.)
stimulierte Ramanstreuung (SRS), gemessen an der Tropfenkette. Relativ
zur Intensität der SRS verschwindet die OH-Bande des Wassers im
Untergrund dieses Spektrums.
wellenlängenabhängig ist. Für eine grobe Abschätzung oder die Ermittlung einer
Tendenz ist „Chyleks Beziehung“ aber auch hier sehr nützlich.
Aus Bild 2.5 läßt sich weiter ersehen, daß die Intensitäten der Resonanzen mit
steigendem Ramanuntergrund zunehmen. Das liegt daran, daß die Resonanz sich
proportional zur Intensität der anregenden Wellenlänge verhält. Variiert man die Größe
der Partikel und beobachtet zum Beispiel nur eine Ausgangsresonanz, so erkennt man,
2. GRUNDLAGEN DER LICHTSTREUUNG
48
wie diese Resonanz über das Küvettenramanspektrum wandert1 und relativ zur
jeweiligen Ramanintensität an Intensität zu- oder abnimmt. Auch hier wird deutlich, daß
sich die Ramanstreuung an Mikropartikeln in einen resonanten und einen
nichtresonanten Anteil aufspalten lassen, wie schon aus Gl. 2.97 (S. 45) hervorgeht. Da
die Resonanzen bevorzugt in Oberflächennähe auftreten, kann man aus der Analyse des
resonanten Teils eines Ramanspektrums Informationen aus diesem Bereich gewinnen.
Z.B. läßt sich die Oberflächentemperatur von verdunstenden Wassertropfen ermitteln,
indem man die OH-Bande des Wassers bei vielen leicht variierten Größenparametern
aufnimmt und der resonante Anteil der Spektren vom nichtresonanten Anteil separiert
wird. Addiert man alle resonanten Anteile der Ramanspektren, so erhält man ein
Ramanspektrum, das dem des Küvettenspektrums entspricht. Es enthält jedoch
Temperaturinformationen, die im wesentlichen von der Partikeloberfläche stammen. Mit
dieser
Methode
kann
gezeigt
werden,
daß
die
Oberflächentemperatur
von
Wassertropfen, die in eine trockene Stickstoffatmosphäre fallen, etwa 4°C kälter ist, als
die gleichen Tropfen, die in eine mit Wasserdampf gesättigte Atmosphäre fallen, wobei
die Temperaturmessungen aus den nichtresonanten Anteilen unwesentlich variierten
[MOR 95]
. Die Tropfen hatten eine Größe von etwa 45 µm und hielten sich zur Zeit der
Messung ungefähr 0.5 ms in der jeweiligen Atmosphäre auf.
Eine theoretische Arbeit über die Abhängigkeit von Konzentrationsprofilen in
Partikeln, die von Ausgangsresonanzen beeinflußt werden, wurde von Lange et al.
[LAN 96c]
geliefert. Moritz et al.
[MOR 97b]
untersuchten die radiale Gewichtung der
Ramanstreuung von Konzentrationsprofilen in Mikropartikeln.
1
Der Größenparameter x = 2πa/λ muß gleich bleiben, so daß sich bei Änderung der Tropfengröße a die
spektrale Position λ ebenfalls ändert.
RAMANSTREUUNG AN MIKROPARTIKELN
49
Eingangsresonanzen wirken sich nicht nur auf die Intensität des transmittierten
Feldes aus, sondern auch auf das inelastisch gestreute Licht von Mikropartikeln. Da bei
einer Eingangsresonanz das transmittierte Feld ansteigt, nimmt damit die Anregung zur
Ramanstreuung zu und auch die Intensität des gesamten Ramanspektrums. Die Messung
von Eingangsresonanzen durch die elastische Lichtstreung geschieht, indem die
Intensität nur einer Ramanlinie, vorzugweise der intensivsten, gemessen wird, während
die Tropfengröße variiert wird. Dabei können an der spektralen Position der RamanLinie auch Ausgangsresonanzen auftreten, die ebenfalls gemessen werden. Bild 2.6 zeigt
ein Beispiel für die Messung der Resonanzen durch Ramanstreuung an der Tropfenkette.
Zur Messung der Eingangs- und Ausgangsresonanzen im Ramanspektrum von
Frequenz / Hz
287956
274869
262563
250981
240070
229783
220075
210907
202240
0
126
128
130
132
134
136
138
140
142
144
Intensität / willk. Einheiten
309190
Mieparameter x
Bild 2.6: Resonanzen im Ramanstreulicht als Funktion des Mie-Parameters und
der Tropfenerzeugungsfrequenz. Das Streuspektrum wurde 5 mm unterhalb des Tropfengenerators an Tropfen gemessen, die zu gleichen Teilen
aus Wasser und Ethanol bestehen. Der Monochromator stand auf der
stärksten Linie des Ethanols (2940 cm-1). Vergleiche dazu auch Bild 2.3
[LEX 98]
. Jede Spitze in diesem Spektrum entspricht einer Resonanz.
2. GRUNDLAGEN DER LICHTSTREUUNG
50
verdunstenden einzeln levitierten (aufgehängten) Partikeln wird häufig auch die
zeitabhängige Ramanstreuung benutzt
[z.B. MUS 96, KAI 96b]
. Dabei werden Ramanspektren
in kurzen Zeitabständen aufgenommen und in einem Kontourplot dargestellt, wobei
jedes Ramanspektrum als Linie und die Intensität in Falschfarben eingezeichnet ist. In
dieser Form werden alle Ramanspektren zeitlich aneinandergereiht. Eingangsresonanzen
erhöhen, wie schon gesagt, das gesamte Ramanspektrum, sodaß das entsprechende
Ramanspektrum zur jeweiligen Zeit deutlich als rechtwinklige Linie hervortritt.
Ausgangsresonanzen wandern mit der Zeit über das Ramanspektrum, sodaß sich im
Kontourplot schräge, über viele Ramanspektren verlaufende Linien, abzeichnen. Aus
dieser Darstellung der zeitabhängigen Ramanstreuung ist das Verdunstungsverhalten
und/oder die chemische Veränderung der Partikelsubstanz zu erkennen.
In
einigen
Fällen
kann
es
gleichzeitig
zu
einer
Eingangs-
und
einer
Ausgangsresonanz, der sogenannten Doppelresonanz kommen. Dann sind die
Resonanzbedingungen eines Partikels für die einfallende Wellenlänge λ0 und die
Wellenlänge λs der Ausgangsresonanz erfüllt. In dem oben erklärten Bild der
zeitabhängigen Ramanstreuung treten Doppelresonanzen dort auf, wo sich die Linien der
Ausgangsresonanzen und der Eingangsresonanzen kreuzen.
Ramanstreuung bei Konzentrationsgradienten
Wie oben dargestellt, sind das transmittierte Feld und das Dipolfeld innerhalb einer
Partikel stark inhomogen. Die meisten Berechnungen für diese Felder gehen von einer
ebenen einfallenden Welle aus. Bei vielen Experimenten wird die einfallende Welle
durch einen stark fokussierten Laserstrahl mit einem Gaußschen Strahlprofil realisiert.
Mit dieser Problematik beschäftigten sich theoretisch Gouesbet et al.
Barton et al.
[GOU 85]
sowie
[BAR 89]
. Gouesbet gab an, daß ein Durchmesser des Laserfokusses von
fünfmal des Partikeldurchmessers (oder größer) eine gute Näherung einer ebenen Welle
ist. Häufig wird jedoch zugunsten einer höheren Strahlungsflußdichte ein kleinerer
Laserfokus gewählt. Bei Ramanexperimenten an der Tropfenkette wird die Tropfenkette
meistens nicht direkt von dem Laserstrahl getroffen, da die Tropfenkette sehr oft eine
RAMANSTREUUNG AN MIKROPARTIKELN
51
leichte Pendelbewegung im Laserstrahl ausführt. Die Tropfen werden also meistens
etwas seitlich vom Laserstrahl beleuchtet. Den Unterschied zwischen einer
symmetrischen und einer tangentialen Einkopplung des Laserstrahls auf das
Ramanspektrum bei einem vorhandenen Konzentrationsgradienten verdeutlicht Bild 2.7.
Theoretische Arbeiten über sogenannte „off-axis“ eingekoppelte Laserstrahlen wurden
von Khaled et al.
einer
[KHA 93]
Tropfenkette
und Gouesbet et al. [GOU 94] veröffentlicht. Da sich die Tropfen
durch
den
Laserstrahl
bewegen,
erhält
man
unzählige
Beleuchtungszustände, die sich mit der Bewegung der Tropfen ändern. Das bedeutet,
daß die experimentellen von den theoretischen Bedingungen abweichen. Die
Feldverteilungen in den Tropfen der Tropfenkette während der Belichtungsperiode einer
Messung sind daher nicht bestimmbar. Das Meßsignal stammt von einer über die
Belichtungsperiode integrierten Feldverteilung.
Liegt ein homogenes Partikel vor, bei dem die zu messenden chemischen Spezies
gleichmäßig verteilt sind, machen sich die oben beschriebenen inhomogenen
Feldverteilungen im Partikel nicht bemerkbar. Anders verhält es sich jedoch, wenn die
Konzentration einer Spezies inhomogen im Partikel verteilt ist, wie bei schnellen
Absorptions- und Desorptionsprozessen der Fall. In Mikrotropfen können diese
Stofftransportprozesse als diffusionskontrolliert vorausgesetzt werden, so daß sich ein
radiales Konzentrationsprofil ausbildet. In einer Arbeit von Lange et al.
[LAN 96c]
ist die
Wirkung des Konzentrationsgradienten auf die Resonanzen theoretisch untersucht
worden, wobei angenommen wurde, daß der Konzentrationsgradient keinen Einfluß auf
den Brechungsindex hat. Dies ist gerechtfertigt, wenn sich die Brechzahlen der
verschiedenen Komponenten nur wenig unterscheiden oder die Konzentration einer
Komponente klein ist. Das trifft auch bei dem in dieser Arbeit untersuchten
Desorptionsprozeß von Acetylen aus Acetontropfen zu, so daß bei den folgenden
Überlegungen die Annahme eines konstanten Brechungsindex beibehalten wird.
2. GRUNDLAGEN DER LICHTSTREUUNG
52
ClO 4
-
Einkopplung der Strahlung:
Intensität / a.u.
symmetrisch
tangential
HOSO 2
900
950
1000
-
HSO 3
1050
Wellenzahlverschiebung / cm
-
1100
-1
Bild 2.7: Ramanspektren der Reaktionsprodukte (HSO3- und HOSO2-) von SO2(g)
mit Wassertropfen bei verschiedenen Beleuchtungszuständen (rechts)
[MOR 95]
. Das ClO4- dient als interner Standard, auf das die Messungen
normiert wird. Dem oberen Spektktrum ist ein Off-set beaufschlagt. Man
sieht, daß die Reaktionsprodukte beim tangentialen Einkoppeln der
Laserstrahlung
ein
höheres
Ramansignal
aufweisen,
als
beim
symmetrischen Einkoppeln. Die Reaktionsprodukte sind zu diesem
Absorptionszeitpunkt vornehmlich in der Nähe der Partikeloberfläche.
Beim tangentialen Einkoppeln des Laserstrahls in das Partikel ist die
Verteilung der anregenden Strahlung in der Nähe der Partikeloberfläche
relativ höher, als bei der symmetrischen Einkopplung.
Für die gemessene Intensität einer Raman-Linie ist in Gl. 2.59 (S. 29) eine homogene
Verteilung der Konzentration cA einer Spezies A vorausgesetzt. Desorbiert die Spezies A
aus einem Partikel, so stellt sich ein Konzentrationgradient ein und die Konzentration in
Oberflächennähe ist geringer als innerhalb des Partikels. Da im Resonanzfall die
Feldverteilung in Oberflächennähe größer ist, kommt mehr Ramansignal aus dem
Bereich der Partikel, in dem die Konzentration von A geringer ist. Dadurch mißt man
eine scheinbare mittlere Konzentration c ∗A , die geringer ist, als die wahre mittlere
Konzentration. In Gl. 2.59 muß daher cA gegen c ∗A ausgetauscht werden. Um eine
RAMANSTREUUNG AN MIKROPARTIKELN
53
Beziehung zwischen der scheinbaren und der mittleren Konzentration herzustellen, muß
man eine radiale Gewichtung der wahren Konzentrationsverteilung vornehmen, die die
inhomogene Feldverteilung im Partikel berücksichtigt:
c ∗A =
1
Vt
∫ w( r )
c A ( r ) r 2 drdΩ .
(2.98)
Vt ist das Tropfenvolumen, auf das das Volumenintegral normiert werden muß. w(r) ist
eine noch beliebige Gewichtungsfunktion. Der differentielle Streuquerschnitt in Gl. 2.59
wird nicht gemäß Gl. 2.97 (S. 45) aufgespalten, da die Streugeometrie im Partikel nun
durch die Gewichtungsfunktion berücksichtigt wird. Für die Gewichtungsfunktion bietet
sich eine einfache rotationssymmetrische Sprungfunktion an, die das Partikel in einen
Kern und eine Hülle aufteilt. Die Sprungstelle b = a
3
2 wird so gewählt, daß der Kern
und die Hülle dasselbe Volumen einnehmen:
1
w0
w( r , x ) =
⎧⎪ h1
⎨
h
⎩⎪ 2
für
0≤r≤b
für
b≤r≤a
.
(2.99)
h1 und h2 sind zwei dimensionslose Faktoren, die die Höhe der Gewichtung angeben.
Ein Parameter x = h2/h1 beschreibt die relative Gewichtung von Hülle und Kern. Den
Normierungsfaktor w0 erhält man aus der Normierungsbedingung für die Gewichtungsfunktion
1 =
1
Vt
a
∫ w( r, x )
r 2 drdΩ =
0
1
( h1 + h2 ) .
2
(2.100)
Damit erhält man die folgende Gewichtungsfunktion:
⎧ 2
⎪⎪
w( r, x ) = ⎨ 1 + x
⎪ 2x
⎪⎩ 1 + x
für
0≤r≤b
.
für
b≤r≤a
(2.101)
2. GRUNDLAGEN DER LICHTSTREUUNG
54
Diese Gewichtungsfunktion würde für x = 1 die korrekte mittlere Konzentration c ∗A = cA
liefern. Damit lautet Gl. (2.98)
c ∗A
6
= 3
a (1 + x )
b
∫
0
6x
c A (r ) r dr + 3
a (1 + x )
2
a
∫
c A (r ) r 2 dr
(2.102)
b
wobei der erste Term die mittlere gewichtete Konzentration im Kern und der zweite die
der Hülle der Partikel bedeuten. Die bei der Gewichtung x zu erwartende scheinbare
mittlere Konzentration c ∗A muß nun mit den Meßwerten verglichen werden. Diese erhält
man aus Gl. 2.64 (S. 31), bei der jedoch von einem homogenen Gemisch ausgegangen
wird. Deshalb muß dort cA gegen c ∗A ausgetauscht werden. Dies ergibt
c ∗A = c B ⋅
IA
IB
⎛c ⎞
⎛I ⎞
⋅⎜ B ⎟ ⋅⎜ A ⎟
.
⎝ I A ⎠ kal ⎝ c B ⎠ kal
(2.103)
Durch eine nichtlineare Anpassung von Gl. 2.102 an die Meßwerte entsprechend
Gl. 2.103 erhält man nun das Gewichtungsverhältnis x. Damit ist auch die in Gl. 2.102
enthaltene tatsächliche Konzentration cA bestimmt. Sie bekommt man, wenn in Gl. 2.102
nicht das ermittelte Gewichtungsverhältnis x, sondern x = 1 gesetzt wird.
Das radiale Profil von verdunstenden Wasser / Methanol - Tropfen wurde von Lin
und Campillo [LIN 95] untersucht. Das leichter flüchtige Methanol verdunstete wesentlich
schneller als das Wasser, so daß sich ein Konzentrationsgradient ausbildete. Es wurden
Ramanspektren in dem Wellenzahlbereich aufgenommen, in dem die OH-Bande des
Wassers und die CH-Bande des Methanols zu sehen sind. Den Spektren sind
Ausgangsresonanzen der ersten drei Ordnungen überlagert. Das Maximum der radialen
Intensitätsverteilung wandert mit zunehmender Resonanzordnung in Richtung der
Partikelmitte (siehe dazu Bild 2.4), so daß die verschiedenen Ordnungen unterschiedlich
vom Konzentrationsgradienten betroffen werden. Durch den Vergleich von Intensitäten
der Resonanzen gleicher Ordnung, die entweder im spektralen Bereich des Wassers oder
des Methanols aufzufinden waren, wurden Rückschlüsse auf das Verhältnis
RAMANSTREUUNG AN MIKROPARTIKELN
55
Methanol / Wasser in Abhängigkeit zum Radius gezogen. Nicht berücksichtigt wurde
hier jedoch ein sich einstellender Brechungsindexgradient.
Aus
dem
Brechungsindexgradienten
von
DBP / Frigen - Tropfen,
ausschließlich das Frigen verdunstete, wurde von Devarakonda et al.
[DEV 98b]
wobei
auf den
Konzentrationsgradienten geschlossen. Der Brechungsindexgradient wiederum wurde
aus den Resonanzpositionen des elastisch gestreuten Lichts (vergleiche dazu Bild 2.3,
S. 40) und aus den Eingangsresonanzen im Ramanstreulicht (vergleiche dazu Bild 2.6,
S. 49) gewonnen.
Nichtlineare Effekte
Treten Strukturresonanzen auf, wird das transmittierte Feld in Mikropartikeln stark
erhöht (s. Kap. 2.2, S. 32ff). Wird unter diesen Bedingungen das einfallende Feld bis zu
einem bestimmten Schwellwert erhöht, kann es zu nichtlinearen Prozessen kommen, wie
z.B. der stimulierten Ramanstreuung (SRS) und der Laseremission. Weitere nichtlineare
Prozesse seien hier nur stichwortartig erwähnt: die stimulierte Brillouinstreuung [ZHA 89],
die stimulierte Rayleigh“wing“streuung [LIN 94] und das „four-wave mixing“ [HSI 88].
Die SRS tritt in transparenten Partikeln auf, wenn das Feld zur Anregung der
Ramanstreuung so hoch ist, daß das induzierte Dipolmoment nicht mehr wie in Gl. 2.9
(S. 8) durch einen einzelnen linearen Term beschrieben werden kann, sondern noch
Terme höherer Ordnungen berücksichtigt werden müssen, wie in Gl. 2.49 (S. 25)
ausgeführt. Das anregende elektrische Feld wird dann so groß, daß die sehr kleinen
Werte der Polarisierbarkeitstensoren höherer Ordnung kompensiert werden und die
Terme höherer Ordnung das induzierte Dipolmoment dominieren. Für die SRS ist der
dritte Term in Gl. 2.49 von Bedeutung.
Um das einfallende Feld soweit erhöhen zu können, daß SRS auftritt, muß ein
Hochleistungs-cw-Laser scharf fokussiert, oder ein gepulster Laser eingesetzt werden.
Die Strahlungsflußdichte des Laserstrahls zum Erreichen des Schwellwerts von SRS
wird von Vehring
[VEH 95c]
für Wassertropfen mit einem Durchmesser von 15 bis 75 µm
2. GRUNDLAGEN DER LICHTSTREUUNG
56
mit 0.25 bis 1 MW/cm2, der niedrigste Schwellwert für 30 µm Ethanoltropfen mit
2.1 kW/cm2 angegeben. Bild 2.5b (S. 47) zeigt das Spektrum von SRS über der OHBande des Wassers. Die Linien der SRS sind so intensiv, daß das lineare
Ramanspektrum der OH-Bande in dieser Darstellung schon fast nicht mehr zu erkennen
ist. Aus dem Abstand der SRS-Linien läßt sich mit „Chyleks Beziehung“ (Gl. 2.95) die
Größe der Tropfen abschätzen. SRS wird stärker angeregt, wenn der fokussierte
Laserstrahl nicht zentral auf das Partikel fällt, sondern das Partikel tangential streift. In
diesem Fall wird das meiste Licht so eingekoppelt, daß es im Inneren durch
Totalreflexion verbleiben kann. Für weitere Literaturhinweise und weiterführende
Theorie sei auf die Arbeiten von Vehring
[VEH 95c]
, Snow
[SNO 85]
und Qian
[QIA 86b]
verwiesen.
Laseremission aus Mikrotropfen wird erreicht, wenn dem Tropfenmedium etwas
Laserfarbstoff zugegeben wird. Dem Fluoreszenzspektrum des Laserfarbstoffs können
dann ebenso Ausgangsresonanzen überlagert sein, wie bei einem Ramanspektrum
(s. Bild 2.5a). Für die Wellenlängen dieser Resonanzen ist das Partikel ein guter
optischer Resonator, so daß es bei diesen Wellenlängen zur Laseremission des
Farbstoffs kommen kann. Einen Überblick über die Laseremission von Mikropartikeln
und deren Anwendung wird von Chen et al.
[CHE 96]
gegeben. Aus dem spektralen
Abstand zwischen zwei Laserlinien kann mit Hilfe von „Chyleks Beziehung“ (Gl. 2.95)
die Größe der Tropfen bestimmt werden. Verdunstet ein Tropfen, so daß der
Tropfendurchmesser d um einige nm kleiner wird, so wandern die Laserlinien in den
blauen Spektralbereich. Aus der Verschiebung einer Laserlinie ∆λshift mit der
Wellenlänge λ kann auf die Änderung des Tropfendurchmessers ∆d geschlossen werden
[CHE 96, TZE 84b]
:
∆λ shift
∆d
=
λ
d
.
(2.104)
RAMANSTREUUNG AN MIKROPARTIKELN
57
Auf diese Weise wurden Verdunstungsraten oder Verbrennungskonstanten bestimmt
[SAN 98]
. Weitere Arbeiten über die Laseremission von Tropfen sind in [CAM 91, QIA 86, TZE 84]
zu finden.
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
58
3 Transportprozesse an Mikropartikeln
3.1 Einleitung
Eine wichtige Rolle bei der Verdunstung von Mikropartikeln spielen Transportprozesse. Dabei handelt es sich im wesentlichen um den Transport von Energie und
chemischen Stoffen. In vielen natürlichen und technischen Systemen finden diese
Prozesse statt. In der chemischen Verfahrenstechnik wird die Stoffumsetzung an
Aerosolen zur Reinigung von Gasen, z.B. der Filtrierung von SO2, genutzt. In der
Lebensmittel- und Baustoffindustrie spielt die Verdunstung bei der Trocknung zu
pulverförmigen Produkten eine große Rolle. Schneller als bei der Verdunstung laufen
Transportprozesse bei der Verbrennung ab. Hier handelt es sich um schnell ablaufende
chemische Reaktionen, bei der Energie freigesetzt wird. Für diesen Fall ist der Stoffund Energietransport besonders deutlich erkennbar. Der Wirkungsgrad und die
Schadstoffemission von Verbrennungsanlagen kann durch die Eigenschaften von
Brennstoffsprays beeinflußt werden.
Untersuchungen der Transportprozesse sind auch deswegen von besonderer
Bedeutung, weil sich in Mikrotropfen Zustände (Übersättigung, Unterkühlung)
einstellen können, die bei Untersuchungen an Proben, die in Kontakt mit festen Wänden
sind, nicht beobachtet werden. Da Mikropartikel eine relativ zu ihrem Volumen große
Oberfläche besitzen, können sie sehr reaktiv sein, was viele Prozesse beeinflußt.
Die relativ große Oberfläche von submikronen Tropfen führt dazu, daß durch die
Oberflächenspannung der Druck im Tropfen erhöht wird. Durch diesen sogenannten
Kelvin-Effekt ändern sich die Phasengleichgewichtsbedingungen an der Tropfen-
TRANSPORTPROZESSE INNERHALB VON MIKROPARTIKELN
59
oberfläche, was wiederum die Transportprozesse beeinflußt. Der Kelvin-Effekt spielt
jedoch bei den in dieser Arbeit untersuchten Prozessen keine Rolle.
Standardwerke über das Verdunstungsverhalten von Aerosolen sind z.B. die
Monographien von Hinds
[HIN 82]
und Fuchs
[FUC 59, FUC 64]
. Über die Wärme- und Stoff-
übertragung im allgemeinen sei auf das Werk von Baehr und Stephan [BAE 94] verwiesen.
Übersichtsartikel zur Verdunstung von Aerosolpartikeln lieferten Vesala et al.
und Annamalai und Ryan
[VES 97]
[ANN 92]
. Im weiteren Verlauf dieses Kapitels werden noch
weitere Literaturhinweise angegeben, die sich dann speziell auf die in dieser Arbeit
behandelte Problematik beziehen.
3.2 Transportprozesse innerhalb von Mikropartikeln
Die beiden hier betrachteten Transportphänomene sind thermisch bedingt und
betreffen sowohl die Wärmeleitung oder den Energietransport als auch die Diffusion
oder den Stofftransport. Die Antriebsfeder beider Prozesse ist ein vorhandener Gradient
entweder in der Temperatur oder in der Konzentration. Die Gleichungen, die diese
Prozesse beschreiben, sind daher sehr ähnlich.
Im Folgenden wird die Temperatur bzw. die Konzentration durch v gekennzeichnet.
Der instationäre Transport von v in sphärischen Polarkoordinaten ist [CAR 59]:
⎧⎪ 1 ∂ ⎛ 2 ∂v ⎞
1
1
∂v
∂ ⎛
∂v ⎞
∂ 2 v ⎫⎪
= κ⎨ 2 ⎜ r
⎟ + 2
⎜ sin θ ⎟ + 2 2
⎬ . (3.1)
⎝ ∂r ⎠
∂t
∂θ ⎠
r sin θ ∂θ ⎝
r sin θ ∂φ 2 ⎭⎪
⎩⎪ r ∂r
κ ist entweder die Temperaturleitfähigkeit oder der Diffusionskoeffizient (beide mit den
SI-Einheiten m2/s). Gl. 3.1 vereinfacht sich für den Fall einer gleichbleibenden
Oberflächentemperatur bzw. -konzentration, so daß v nur von der radialen Koordinate r
und von der Zeit t abhängt
⎛ ∂ 2 v 2 ∂v ⎞
∂v
⎟ .
= κ⎜ 2 +
∂t
r ∂r ⎠
⎝ ∂r
(3.2)
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
60
Die Lösung von Gl. 3.2 für eine Kugel (0 ≤ r < a) mit den Anfangsbedingungen
v(r, t=0) = 0 (Anfangs-Temperatur/Konzentration innerhalb der Kugel gleich Null)
und
v(a, t) = V
(Oberflächen-Temperatur/Konzentration der Kugel bleibt konstant)
ist [CAR 59]
v( r, t ) = V +
∞
2aV
πr
∑
n =1
( −1) n
nπr − κn 2 π 2 t
sin
e
n
a
a2
.
(3.3)
Die über die Kugel gemittelte Temperatur/Konzentration für diesen Fall ist
v( t ) = V −
6V
π2
∞
∑
n =1
1
n2
e − κn
π t a2
2 2
.
(3.4)
Zur Lösung von Gl. 3.2 mit den Anfangsbedingungen
1.0
Konzentration c / c0
0.8
0.6
0.4
0.2
0.0
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Radius r / a
Bild 3.1: Nach Gl. 3.5 berechnete Konzentrationsprofile innerhalb eines Partikels
mit dem Radius r = 24 µm zu den Zeiten 0 ≤ t ≤ 5 ms in Schritten von
0.5 ms für den Diffusionskoeffizienten DAB = 7.1 x 10-9 m2/s.
TRANSPORTPROZESSE INNERHALB VON MIKROPARTIKELN
61
v(r, t=0) = V (Anfangs-Temperatur/Konzentration innerhalb der Kugel ist gleich V)
und
v(a, t) = 0
(Oberflächen-Temperatur/Konzentration der Kugel ist gleich Null)
müssen die Gln. 3.3 und 3.4 von V abgezogen werden.
Für diesen Fall lautet das Konzentrationsprofil im Tropfen bei einem rein diffusiven
Stofftransport (Desorption) wie folgt:
c A (r, t ) = −
2ac0
πr
∞
∑
n =1
( −1)
n
n
⎛ nπr ⎞
sin ⎜
⎟ e
⎝ a ⎠
−
D AB n 2 π 2 t
a2
.
(3.5)
Hierin sind c0 die Anfangskonzentration, r die radiale Position und DAB der
Diffusionskoeffizient der Komponente A in der Komponente B. Dies entspricht dem Fall
des in dieser Arbeit untersuchten Desorptionsprozesses von Acetylen aus Acetontropfen.
Bild 3.1 zeigt einige nach Gl. 3.5 berechnete Konzentrationsprofile zu verschiedenen
Zeiten.
Für Desorptionsprozesse an den Tropfen einer Tropfenkette stellt Gl. 3.5 eine gute
Näherung dar, da der Stofftransport in die Gasphase nicht nur durch Diffusion, sondern
auch durch Konvektion erfolgt. Der desorbierende Stoff wird durch die strömende
Gasphase abtransportiert und die Bedingung der verschwindenden Oberflächenkonzentration ist in guter Näherung gerechtfertigt.
Die charakteristische Zeit τD für die interne Diffusion, d.h. die Zeit, bis ein
exponentiell abnehmender Prozeß auf e-1 abgefallen ist, kann aus Gl. 3.5 entnommen
werden. Betrachtet man nur den ersten Term der Summe, dies ist gerechtfertigt, da der
Beitrag der Terme mit n > 1 keinen wesentlichen Beitrag mehr leistet, so erhält man in
guter Näherung:
τD =
a2
π 2 D AB
.
(3.6)
Für eine Kugel mit dem Radius a = 24 µm und einem Diffusionskoeffizienten von
DAB = 7.1 x 10-9 m2/s erhält man demnach die charakteristische Zeit von etwa 8 ms. Im
Fall der Dimension einer Küvette von z.B. a ≈ 10 mm erhält man eine charakteristische
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
62
Zeit von etwa einer halben Stunde. Hierbei wird deutlich, wie unterschiedlich die
zeitlichen Verhältnisse zwischen dem Stofftransport an Mikrotropfen relativ zu den für
Menschen alltäglichen Dimensionen ist. Wird in Gl. 3.6 anstelle von DAB die
Temperaturleitfähigkeit gesetzt, so kann man die charakteristische Zeit für einen
Temperaturausgleich abschätzen.
3.3 Transportprozesse mit Berücksichtigung der Gasphase
Bei Stofftransportuntersuchungen an einzeln levitierten Partikeln, bei denen
konvektive Stofftransportprozesse vernachlässigt werden können, muß die Diffusion in
der Gasphase berücksichtigt werden. Dazu sei z.B. auf die Arbeiten von Kaiser [KAI 96b] ,
Ray und Davis
[RAY 80]
sowie Ray und Venkatraman
[RAY 95]
verwiesen. Diese Autoren
benutzen Verdunstungsmodelle, die dem sogenannten „d2-Law“ von Law und
Law [LAW 82]
ähnlich
sind.
Demnach
verringert
sich
das
Quadrat
des
Tropfendurchmessers (oder die Tropfenoberfläche) linear mit der Zeit. Die von diesen
Autoren benutzte Meßmethode der Ermittlung von Resonanzpositionen (siehe Kap. 2.2
und 2.3), die sehr empfindlich von der Partikelgröße abhängen, macht eine
Berücksichtigung der Gasphase notwendig, soweit der Dampfdruck der verwendeten
Flüssigkeit nicht vernachlässigbar klein ist.
Bei Verbrennungsvorgängen geschieht der Stofftransport in die Gasphase so schnell,
daß die Gasphase auch bei Tropfenkettenexperimenten berücksichtigt werden muß.
Hierbei findet eine Wechselwirkung zwischen Tropfen statt, die den Stofftransport
empfindlich beeinflußt.
Aus der Fülle der Veröffentlichungen über Verbrennungs- und Verdunstungsvorgängen von Mikrotropfen seien im Folgenden einige Ansätze beschrieben, die dem in
dieser Arbeit untersuchten Prozeß Nahe kommen. Leider handelt es sich dabei meistens
um Einzelaspekte, die den gesamten komplexen Vorgang nur partial beschreiben.
Den Einfluß der Tropfenkette auf die Strömung des umgebenden Gases haben
Connon und Dunn-Rankin [CON 96] untersucht. Sie haben einzelne Tropfen elektrostatisch
TRANSPORTPROZESSE MIT BERÜCKSICHTIGUNG DER GASPHASE
63
aus dem Tropfenkettenverband ausgelenkt und deren Abbremsverhalten in der
langsameren Umgebungsströmung beobachtet. Mit verschieden starken Auslenkungen
der Meßtropfen konnten sie das Strömungsfeld um eine Tropfenkette bestimmen. Ihr
wesentliches Ergebnis war, daß eine Tropfenkette ihre Umgebung um etwa 15
Tropfendurchmesser beeinflußt.
Bei einem Ensemble von Tropfen ist naheliegenderweise die Wechselwirkung
zwischen den Tropfen der wesentliche Unterschied zu Einzeltropfen. Da die
Untersuchung und Berechnung von Einzelpartikelprozessen in vieler Hinsicht einfacher
ist, werden häufig bei der Charakterisierung von Partikelensemblen Vergleiche zu
Einzelpartikeln gezogen. Dies führt zu einem Wechselwirkungsparameter η, der die
Rate von Transferprozessen eines Tropfens in einem Tropfenensemble auf die eines
einzelnen Tropfens bezieht. Eine Folge der Wechselwirkung zwischen den Tropfen ist,
daß das oben erwähnte „d2-Law“ nicht mehr ohne weiteres angewandt werden kann. Der
Wechselwirkungsparameter hängt von vielen Faktoren ab, wie z.B. der Geometrie der
Tropfenanordnung, dem Abstand zwischen den Tropfen, der Tropfengröße, der
Tropfenzusammensetzung und der Gasphase zwischen den Tropfen. Im Folgenden wird
der Wechselwirkungsparameter auf eine Tropfenkette und den auf den Tropfendurchmesser bezogenen Abstand zwischen den Tropfen
ε = l a
(3.7)
betrachtet. l ist der Abstand zwischen den Partikelmittelpunkten.
Der Wechselwirkungsparameter als effektive Reduzierung der Verdunstungsrate ist
wie folgt definiert:
η =
d
dt
d
dt
mTK
mEP
,
(3.8)
wobei mTK die verdunstete Masse eines Tropfenkettenpartikels und mEP die eines
Einzelpartikels ist. Im allgemeinen gilt: η < 1. Wechselwirkungsparameter für
verschiedene geometrische Partikelanordnungen wurden von Ray und Davis
[RAY 80]
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
64
berechnet. Annamalai und Ryan [ANN 92] bestimmten den Wechselwirkungsparameter für
eine Kette aus N monodispersen Tropfen:
⎡
⎛ a⎞
η = ⎢1 + ⎜ ⎟ sin( π / N )
⎝l⎠
⎢⎣
∑
i
⎤
1
⎥
sin(iπ / N ) ⎦⎥
−1
,
(3.9)
wozu sie ein sogenanntes Punkt-Quellen-Modell (PSM, point source model) benutzten,
in dem alle Tropfen durch Punktmassen ersetzt wurden.
Eine Reihe von Forschern haben den Wechselwirkungsparameter für unterschiedliche
Verdunstungsbedingungen experimentell bestimmt. Silverman und Dunn-Rankin
[SIL 94]
haben die Wechselwirkungsparameter für die Verdunstungs- und Verbrennungsrate von
verschiedenen Brennstoffen gemessen. Dazu wurden die Tropfenabstände ε variiert, die
Tropfendurchmesser jedoch konstant bei etwa 100 µm gehalten. Dies wurde erreicht,
indem der Blendendurchmesser und die Flußrate des Brennstoffs geschickt gewählt
wurden (vergleiche dazu auch Kap. 4.2). Bei der Verdunstung der Hexantropfen mit
relativen Tropfenabständen von ε = 2.0, 3.9 und 5.5 wurden entsprechende Wechselwirkungsparameter von η = 0.31, 0.46 und 0.55 gemessen.
Devarakonda et al.
[DEV 98]
und Devarakonda [DEV 98c] untersuchten das Verdunstungs-
verhalten von Ethanoltropfen mit einem Anfangsdurchmesser von 22 µm. Bei dem
relativen Tropfenabstand von ε ≈ 4 betrug der Wechselwirkungsparameter η = 0.35
(bzw. η = 0.28 für ε ≈ 3.5). Aus ihren Modellen hat Devarakonda den Einflußbereich der
Gasphase um verdunstende Ethanoltropfen mit etwa 20 Tropfendurchmessern
abgeschätzt. Dies ist in etwa das gleiche Ergebnis wie das von Connon und DunnRankin [CON 96], wie oben erwähnt, deren Wassertropfen jedoch etwa 5 bis 6 mal so groß
waren.
Eine andere Modellvorstellung wurde von Umemura [UME 90] veröffentlicht. Demnach
werden zuerst zwei Einzeltropfen aus dem Unendlichen zusammengeführt, die sich
immer mehr beeinflussen. Zwischen den Tropfen existiert eine flußfreie Linie (bei
zweidimensionaler Betrachtung), durch die weder Energie- noch Stoffaustausch
stattfindet. Bei einer ruhenden Gasphase befindet sich diese Linie genau in der Mitte
TRANSPORTPROZESSE MIT BERÜCKSICHTIGUNG DER GASPHASE
65
zwischen den Tropfen. Durch Hinzuführen weiterer gleichgroßer Tropfen wird eine
monodisperse Tropfenkette konstruiert. Nach wie vor ruht die Gasphase relativ zu den
Tropfen, so daß in der Mitte zwischen allen Tropfen eine flußfreie Linie existiert. Bei
einem relativen Tropfenabstand von ε ≈ 10 oder größer kann man in guter Näherung von
einem System isolierter Tropfen ausgehen. Dies ändert sich, wenn die Geschwindigkeit
der Gasphase größer als Null wird. In diesem Fall wandert die flußfreie Linie aus der
Mitte zwischen den Tropfen in Richtung des Gasflusses auf den nächsten Tropfen zu.
Der Abstand zwischen der Lage der flußfreien Linie zur Mitte zwischen den Tropfen ist
ein Maß für die Wechselwirkung zwischen den Tropfen.
Bei den oben beschriebenen Modellen werden Vergleiche zum Einzeltropfen
gezogen. Das bedeutet, daß die Prozesse und Stofftransportdaten bekannt sein müssen.
Bei dem in dieser Arbeit untersuchten Desorptionsprozeß war der Diffusionskoeffizient
von Acetylen in Aceton unbekannt und mußte erst durch Tropfenkettenexperimente
ermittelt werden. Somit lagen keine Ergebnisse von Einzeltropfenexperimenten oder berechnungen vor. Auf eine weitere eingehendere theoretische Betrachtung, die auf dem
Vergleich zu Einzeltropfenergebnissen beruht, wurde daher verzichtet.
Bei allen gefundenen Modellen, die Prozesse an der Tropfenkette beschreiben, wird
von monodispersen Tropfen ausgegangen, die in einem äquidistanten Abstand
zueinander angeordnet sind. Dies ist nur in den ersten Millimetern nach dem
Tropfenzerfall in guter Näherung gegeben. Schon ab etwa 10 mm unterhalb des
Schwingblendengenerators (SBG) ist kein einheitlicher Tropfenabstand, sondern eine
Abstandsverteilung meßbar. Dies kann man sehr einfach anhand der Interferenzmuster
sehen, wenn die Tropfenkette mit Laserlicht beleuchtet wird (siehe dazu Kap. 4.2 und
Bild 4.4, S. 88). Aber auch bei den sehr empfindlichen Tropfengrößenmessungen mittels
MDRs
(s.o.)
wird
dies
deutlich,
da
man
durch
die
breiter
werdende
Tropfenabstandsverteilung keinen festen Wechselwirkungsparameter mehr bekommt,
sondern auch hier eine Verteilung. Dies hat zur Folge, daß auch die Tropfengröße für
zunehmende Abstände eine breiter werdende Verteilung erhält, so daß schmale MDRs
nicht mehr gemessen werden können [CAM 98]. Aus diesem Grunde messen viele Forscher
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
66
(z.B. die Gruppen um A. J. Campillo und A. K. Ray) nur innerhalb der ersten 10 mm
unterhalb des SBG. Bei weiter zunehmendem Abstand zum SBG können sich die
Tropfen sogar soweit nähern, daß es zu Tropfenkoagulationen kommt [AND 92]. Weiterhin
wandern die Tropfen ab einem bestimmten Abstand aus dem linearen Verband der
Tropfenkette und es entsteht ein Spray. Modelle, die das Verdunstungsverhalten von
monodispersen Tropfenketten mit nichtäquidistantem Tropfenabstand (d.h. für große
Fallstrecken oder lange Tropfenlebensdauern) beschreiben, wurden vom Autor nicht
gefunden.
Durch
die
oben
beschriebene
Problematik
der
Modellierung
des
Verdunstungsverhaltens von Tropfenketten im allgemeinen und der Gasphase im
speziellen ist es daher besonders wichtig, Meßmethoden zu entwickeln, mit denen der
Verdunstungsprozeß ermittelt werden kann. Eine Methode zur Messung der
Flüssigphase sowie der Gasphase zwischen den Acetylen / Acetontropfen an der
Tropfenkette wird in Kap. 5 (S. 124ff) vorgestellt. Mit den dort präsentierten
Ergebnissen und Meßmethoden können bisherige und neue Modelle getestet werden.
3.4 Dampfdruck
Der Dampfdruck ist der Druck der Gasphase eines Stoffes, bei der Gas und
Flüssigkeit für eine bestimmte Temperatur im Gleichgewicht sind. Er ist daher ein Maß
für die zwischenmolekularen Bindungskräfte. Mit steigender Temperatur nimmt der
Dampfdruck zu. Für einen konstanten Umgebungsdruck, der größer als der Dampfdruck
ist, ist der Dampfdruck ein Maß für die Verdunstung eines Stoffes. In diesem Fall stellt
sich
kein
Phasengleichgewicht
ein.
Die
zur
Verdunstung
notwendige
Verdampfungsenthalpie wird der Flüssigkeit entzogen, die sich damit abkühlt.
Zur Bestimmung des Dampfdrucks Pvp eines Stoffes für eine bestimmte Temperatur T
sei auf das Standardwerk von Reid, Prausnitz und Poling [REI 86] verwiesen. Hier werden
für viele Stoffe die jeweilige Näherungsgleichung des entsprechenden Stoffes zur
Bestimmung des Dampfdrucks angegeben. Die Näherungsgleichungen enthalten die
DAMPFDRUCK
67
Dampfdruckkonstanten A, B, C und/oder D, die ebenfalls aufgelistet sind. Diese
Konstanten für einen Stoff beziehen sich jedoch nur auf die entsprechende Näherungsgleichung des Stoffes.
Eine häufig angewandte Gleichung ist die Dampfdruckkorrelation von Antoine
[ANT 88, REI 86]
:
B ⎞
⎛
Pvp = exp ⎜ A −
⎟
⎝
T − C⎠
,
(3.10)
deren Anwendungsbereich nur im Druckbereich von etwa 0.01 bis 2 bar und in einem
kleinen Temperaturbereich liegt. Für die meisten Stoffe wird die folgende Gleichung
gewählt [REI 86]:
⎛ Aτ + Bτ1.5 + Cτ 3 + Dτ 6 ⎞
⎟
Pvp = Pc ⋅ exp ⎜
1− τ
⎝
⎠
,
(3.11)
wobei
τ = 1 −
T
Tc
und Pc bzw. Tc der kritische Druck bzw. die kritische Temperatur sind. Eine
Auflistung der Konstanten für einige Stoffe ist in Tab. 3.1 zu finden. Exemplarisch ist in
Bild 3.2 die temperaturabhängige Dampfdruckkurve für Chlorethan dargestellt.
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
68
Tabelle 3.1: Konstanten zur Berechnung des Dampfdruckes nach Gl. 3.11 [
Substanz
Tc / K
A
Pc / bar
B
REI 86]
.
C
D
Aceton
508.1
47.0
-7.45514
1.20200
-2.43926
-3.35590
Acetylen
308.3
61.4
-6.90128
1.26873
-2.09113
-2.75601
Ethanol
513.9
61.4
-8.51838
0.34163
-5.73683
8.32581
Wasser
647.3
221.2
-7.76451
1.45838
-2.77580
-1.23303
Chlorethan
460.4
52.7
-7.23667
2.11017
-3.53882
0.34775
Dampfdruck / bar
1
0.1
0.01
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
Temperatur / °C
Bild 3.2: Dampfdruck als Funktion der Temperatur für Chlorethan (C2H5Cl),
berechnet nach Gl. 3.11. Bei Atmosphärendruck (1 bar) wird das
Chlorethan oberhalb von T = 12.4°C (Siedepunkt) gasförmig.
DIE LÖSLICHKEIT VON GASEN IN FLÜSSIGKEITEN
69
3.5 Die Löslichkeit von Gasen in Flüssigkeiten
Die Löslichkeit von Gasen in Flüssigkeiten spielt eine wichtige Rolle für die
Untersuchung der Transportprozesse in dieser Arbeit. Sie ist ein Kriterium für die
Auswahl des Systems Acetylen / Aceton, das hier an der Tropfenkette untersucht wird.
Ist eine Lösung im Gleichgewicht mit einer gegebenen Temperatur und Druck, so
wird die gelöste Menge durch den Löslichkeitskoeffizienten zum Ausdruck gebracht. Im
Grenzfall unendlich verdünnter Lösungen
[WIL 77]
ist die in einer Flüssigkeitsmenge
gelöste Gasmenge dem Partialdruck des Gases in der Gasphase proportional.
Vorausgesetzt wird, daß sich die Komponenten nicht chemisch beeinflussen. Für binäre
Systeme gilt daher [LAN 76]:
m = k ⋅ mLM ⋅ P ,
(3.12)
wobei m die Masse des gelösten Gases, k der temperaturabhängige Löslichkeitskoeffizient, mLM die Masse des Lösungsmittels und P der Partialdruck des gelösten
Gases ist. Je nach den verwendeten Einheiten der in Gl. 3.12 vorkommenden Größen
gibt es verschiedene Definitionen des Löslichkeitskoeffizienten. Im Folgenden wird in
Anlehnung an das Zahlenwerk Landolt-Börnstein
[LAN 76]
der Löslichkeitskoeffizient in
Form des „technischen Löslichkeitskoeffizienten“ wiedergegeben. Beim technischen
Löslichkeitskoeffizienten λ wird die gelöste Gasmenge durch das Normvolumen VN
ausgedrückt, die Menge mLM des Lösungsmittels in Tonnen (t) und der Partialdruck P in
Atmosphären (at) angegeben. Damit ist
λ =
VN
.
mLM P
(3.13)
In Tab. 3.2 sind die Löslichkeitskoeffizienten einiger Gas / Flüssigkeitssysteme
zusammengefaßt.
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
70
Tabelle 3.2: Löslichkeitskoeffizienten λ für verschiedene Gas / Flüssigkeitssysteme
bei T = 25°C und P = 1 bar in Nm3/(t at) [
Gas
C2H2
Flüssigkeit
C3H6
SO2
LAN 76]
.
CO2
NH3
CH5N
Aceton
28
16
350
7.5
-
-
Wasser
0.9
0.12
30
0.7
620
2200
Ethanol
7
-
120
0.35
150
-
Methanol
13
9
240
4.5
280
-
Häufig wird zur Angabe der Löslichkeit der Henry-Koeffizient H verwendet. Ihn
bekommt man, wenn man nicht wie in Gl. 3.12 die Masse m des gelösten Gases als
Funktion des Partialdruckes P, sondern umgekehrt den Partialdruck des Gases als
Funktion seines Molenbruchs x in der Lösung betrachtet. Man erhält dann das HenryDaltonsche Gesetz in der Form
H =
P
.
x
(3.14)
Der Henry-Koeffizient H hat die Dimension eines Druckes und kann als ein fiktiver
Dampfdruck des gelösten Gases im verflüssigt gedachten Zustand bei der fraglichen
Temperatur betrachtet werden.
Die
Umrechnung
vom
technischen
Löslichkeitskoeffizienten
zum
Henry-
Koeffizient H geschieht mit:
H =
ρ LM
⋅λ ,
VN
(3.15)
wobei ρLM die Dichte des Lösungsmittels ist.
Kann man die Lösung nicht mehr als ideal verdünnt betrachten, so tritt an die Stelle
des Henry-Daltonschen Gesetzes das Raoultsche Gesetz
DIE LÖSLICHKEIT VON GASEN IN FLÜSSIGKEITEN
71
1.6
Acetylen-Konzentration / mol/l
1.5
1.4
1.3
1.2
1.1
1.0
0.9
0.8
0.7
0.6
0.5
0.4
10
15
20
25
30
35
40
Temperatur / °C
Bild 3.3: Gemessene Acetylenkonzentration in Aceton in Abhängigkeit zur
Temperatur. Die Messung wurde an einer Küvette vorgenommen. Die
Meßmethode wird in Kap. 5 beschrieben.
x =
P
Pvp
,
(3.16)
in dem Pvp der Dampfdruck des reinen verflüssigten Gases ist. Die Darstellung des
Raoultschen Gesetzes in Gl. 3.16 wird deshalb so gewählt, um die Temperaturabhängigkeit auf die Menge des eingelösten Stoffes x zu verdeutlichen. Dies geht
unmittelbar aus der Temperaturabhängigkeit des Dampfdruckes (s.o.) hervor. Gleiches
gilt für das Henry-Daltonsche Gesetz (Gl. 3.14). Diese Abhängigkeit ist in Bild 3.3
verdeutlicht, in der eine Messung der in Aceton eingelösten Acetylenkonzentration in
Abhängigkeit zur Temperatur gezeigt wird.
3. TRANSPORTPROZESSE AN MIKROPARTIKELN
72
3.6 Fazit
Für die Modellierung der Stoffverteilung eines Gases innerhalb von Mikrotropfen
stellt Gl. 3.5 eine gute Näherung dar. Wichtiger als die nicht verschwindende
Oberflächenkonzentration, die in Gl. 3.5 vorausgesetzt wird, ist die Berücksichtigung
der
inhomogenen
Feldverteilung
innerhalb
des
Tropfens
bei
einem
Konzentrationsgradienten der zu messenden Spezies, wie es in Kap. 2.3 (Ramanstreuung
an Mikropartikeln) ausgeführt wurde. Dieses theoretische Konzept wird für die in Kap. 5
vorgestellten Messungen angewendet und diskutiert.
Für die Modellierung der Gasphase werden einige theoretische Einzelkonzepte aus
der Literatur vorgestellt. Diese beziehen sich auf Transportprozesse von Einzeltropfen.
Für das in dieser Arbeit untersuchte System ist der Diffusionskoeffizient nicht bekannt,
so
daß
Vergleiche
mit
Einzeltropfenprozessen,
z.B.
die
Bestimmung
des
Wechselwirkungsparameters, nicht gezogen werden können. Wichtiger für diese Arbeit
war die Entwicklung einer Meßmethode zur Ermittlung der Gasphasenkonzentration in
unmittelbarer Nähe der Tropfen, sprich zwischen den Tropfen. Dies wird in Kap. 5
(S. 124ff) noch vorgestellt. Mit den Ergebnissen aus den Messungen nach dieser
Methode lassen sich dann neue Modelle testen.
Im weiteren wird ein System gesucht, an dem der Stofftransport mittels der RamanSpektroskopie gut zu untersuchen ist. Dazu mußte ein Stoffsystem verschiedene
Kriterien erfüllen: Eine Komponente soll eine hohe Löslichkeit in der anderen haben
sowie einen hohen Dampfdruck. Die andere Komponente soll relativ zur ersten einen
niedrigen Dampfdruck besitzen. Damit bietet sich ein Gas / Flüssigkeitssystem an. Ein
weiteres Kriterium ist die Meßbarkeit im Ramanspektrum: Die Raman-Linien der
einzelnen Komponenten sollten spektral dicht beeinander liegen, jedoch gut trennbar
voneinander sein. Dies gilt auch für die Linien unterschiedlicher Phasen einer
Komponente, sowie für Linien von Komponenten, die als interner Standard eingesetzt
werden. Weiterhin sollen die Komponenten nach Möglichkeit ungiftig, ungefährlich und
FAZIT
73
leicht zu handhaben sein. Den besten Kompromiß zur Erfüllung dieser Kriterien bietet
das System Acetylen / Aceton.
Mit dem System Acetylen / Aceton kann die Konzentration des Acetylen im gelösten
Zustand innerhalb des Tropfens sowie im freigesetzten Zustand in der Gasphase um die
Tropfen gemessen werden. Wünschenswert ist es, ein System zur Verfügung zu haben,
an dem zusätzlich die Temperatur des Tropfens und der Gasphase um die Tropfen
gemessen werden kann. Damit kann ein Verdunstungsprozeß vollständig vermessen
werden. Eine Temperaturmessung ist jedoch nur mit anderen Systemen möglich. Die
Messung der Temperatur des Tropfens kann mit reinem Wasser gemacht [VEH 92] und die
Temperatur der Gasphase prinzipiell mit dem Rotations-Raman-Effekt gemessen werden
(siehe dazu Kap. 2.1.4, S. 28f). Dazu bietet sich für die meisten Fälle Stickstoff an, da es
ein inertes Gas und in der Luft mit großem Anteil enthalten ist. Die Messung der
Gastemperatur mit dem Rotations-Raman-Effekt ist jedoch nicht sehr empfindlich,
sodaß eine Abkühlung durch Verdunstung schon mehrere 10 K betragen muß. Dies kann
man mit Chlorethantropfen (C2H5Cl) erreichen, da Chlorethan schon bei 12.4°C
verdampft und so bei umgebender Raumtemperatur ein großer Stofftransport stattfindet,
der eine Abkühlung von etwa bis zu 50 K ermöglicht.
4. EXPERIMENTELLER AUFBAU
74
4 Der experimentelle Aufbau
Die Raman-Spektroskopie existiert seit über 70 Jahren. Bis in die Mitte der sechziger
Jahre wurden als Anregungslichtquellen hauptsächlich Quecksilberhochdruck- und
Quecksilberniederdrucklampen eingesetzt. Mit der Einführung des Lasers im Jahre 1960
hat die Entwicklung der Raman-Spektroskopie einen enormen Schub bekommen. Etwa
zur gleichen Zeit wurden auch die Detektionsmöglichkeiten verbessert. Photografische
Platten wurden durch Photomultiplier und Prismen-Spektrographen durch GitterSpektrographen ersetzt. Die Entwicklung setzte sich fort und heute werden häufig
mehrstufige Spektrographen und CCD-Kameras eingesetzt.
Bisherige experimentelle Untersuchungen
Ramanspektroskopische
Untersuchungen
an
einzelnen
optisch
[THU 84, THU 85]
Mikropartikeln wurden erstmals von Thurn und Kiefer
optische Levitation von Mikropartikeln gelang zuerst Ashkin
levitierten
publiziert. Die
[ASH 70]
. Eine Übersicht
über die experimentellen Arbeiten zur Aerosolanalyse mittels der Raman-Spektroskopie
bis zum Jahr 1990 wird von Schweiger
[GS 90]
gegeben. Weitere Arbeiten zur optischen
Levitation und zur Raman-Spektroskopie kamen ebenfalls von Schweiger
91a+b, 92, 94, 97]
.
Das
Streulichtverhalten
geschichteter
Partikel
und
[GS 87, 89, 90a-d,
einen
guten
Literaturüberblick über die optische Levitation findet man bei Kaiser [KAI 96]. Esen et al.
[ESE 95]
und
Unterdrückung
des
untersuchten Photopolymerisationsreaktionen an levitierten Partikeln
erzeugten
feste
sphärische
Mikropartikel
[ESE 96, 97]
.
Die
Fluoreszenzuntergrundes durch Photolyse fanden Kaiser et al.
[KAI 96]
an optisch
levitierten Mikropartikeln. Einen Überblick über die Levitation von Mikropartikeln im
allgemeinen präsentiert Davis [DAV 97].
ÜBERSICHT
75
Untersuchungen an einer Kette von monodispersen Mikrotropfen sind seit der
Einführung des Schwingblendengenerators im Jahre 1973 durch Berglund und Liu
[BER 73]
möglich. Die Betriebsweise dieses Generators wurde von Lin et al.
[LIN 90a]
stabilisiert. Ein Modell für das Strömungsfeld um die Tropfen der Tropfenkette wurde
von Liu et al. [LIU 88] entwickelt. Ihre Untersuchungen ergaben einen laminaren Fluß.
Fung und Tang [FUN 92] zeigten an der Tropfenkette, daß die Resonanz-Ramanstreuung
zur Analyse von Mikrotropfen einer wässrigen Lösung aus p-Nitrosodimethylanilin
eingesetzt werden kann. Stimulierte Raman-Streuung (SRS) an einer Kette
monodisperser Wassertropfen mit verschiedenen Ionen untersuchten Serpengüzel et al.
[SER 90]
und Zhang et al.
Vehring
[VEH 95c]
[ZHA 93]
. Die Schwellen zum Einsetzen der SRS werden von
für Mikrotropfen aus Ethanol mit 2.1 kW/cm2 und für Wassertropfen
mit 0.25 bis 1 MW/cm2 angegeben. Fung et al.
[FUN 94]
fanden bei Messungen an einer
Tropfenkette, daß die Nachweisgrenze von Sulfaten und Nitraten, gemessen mit der
linearen Raman-Spektroskopie (LRS), etwa 30 mal empfindlicher ist, als mit der SRS.
Die Temperatur von verdunstenden Mikrotropfen aus Wasser wurde von Vehring und
Schweiger [VEH 92] als Funktion des Abstandes zum Schwingblendengenerator gemessen.
Dabei wurde die temperaturabhängige Deformation der OH-Schwingung des Wassers
genutzt. Basierend auf dieser Meßmethode haben Moritz et al. [MOR 95] die Temperatur in
der Randschicht von Mikrotropfen aus Wasser bestimmt, indem sie die Outputresonanzen im Ramanspektrum analysierten. Das radiale Profil von Mikrotropfen
untersuchten Lin und Campillo [LIN 95] mit Hilfe der Raman-Spektroskopie.
Die Untersuchungsmöglichkeiten von schnellen Transportprozessen und Reaktionen
an Mikrotropfen mit der linearen Raman-Spektroskopie zeigten Vehring et al.
[VEH 95a]
am Beispiel des Desorptionsprozesses von CO2 aus Wassertropfen und des
Absorptionsprozesses von SO2 in Wassertropfen. Bei der Untersuchung des
Absorptionsprozesses
[MOR 94, 96b]
konnte erstmals gezeigt werden, daß die sich beim
Reaktionsprozeß bildenden Hydrogen-Sulfit-Isomere nacheinander entstehen und sich
erst nach etwa 5 ms ein Gleichgewicht zwischen den beiden Formen einstellt. Moritz
et al.
[MOR 96a+b]
bestimmten den Diffusionskoeffizienten von Acetylen in Aceton durch
die Untersuchung des Desorptionsprozesses von Acetylen aus Acetontropfen an einer
Tropfenkette. Eine Auswertung dieser Messungen unter der Berücksichtigung, daß die
4. EXPERIMENTELLER AUFBAU
76
Raman-Streuung innerhalb der Partikel inhomogen verteilt ist, zeigte, daß der größte
Anteil des Raman-Signals aus den oberflächennahen Bereichen stammt [LAN 96b]. Gründe
dafür können einerseits Strukturresonanzen sein, deren Modenvolumen in der Nähe der
Partikeloberfläche liegen (siehe Kap. 2.2 und 2.3, S. 39ff). Andererseits war in den
Experimenten der Laserfokus etwa so groß wie der Partikeldurchmesser, so daß beim
Passieren der Partikel durch den Laserstrahl Oberflächenwellen stärker angeregt werden,
wenn der Laserstrahl die Partikel nicht direkt in der Mitte trifft.
Optische Resonanzen im Streulicht wurden von Devarakonda et al. [DEV 98] sowie von
Lin und Eversole
[LIN 90b; EVE 93+95]
für äußerst präzise Messungen an extrem
monodispersen Mikrotropfen gemessen. Dabei wurden Größe und Brechungsindex der
Partikel mit hoher Präzision bestimmt.
Im Folgenden wird zunächst eine Übersicht des Experiments vorgestellt, die einen
kompakten Gesamteindruck des Versuchsaufbaus vermittelt. Danach wird auf die
Einzelkomponenten des Experiments eingegangen.
4.1 Übersicht
Bild 4.1 zeigt eine Skizze des Versuchsaufbaus. Eine Kette gleich großer
Mikrotropfen wird von einem Schwingblendengenerator (SBG; VOAG, vibrating orifice
aerosol generator)
[BER 73]
erzeugt, dessen Betrieb nach Lin et al.
[LIN 90a]
stabilisiert
wurde. Eine Flüssigkeit wird unter Druck (∆p = 1 - 6 bar) durch eine Blende (Melles
Griot oder Eigenfertigung, ∅i = 5 - 50 µm
Piezokeramik
zu
Schwingungen
[HOC 94]
angeregt,
) gepreßt. Diese wird von einer
die
sich
auf
den
austretenden
Flüssigkeitsstrahl übertragen, der dann bei geeigneten Frequenzen gleichmäßig zerfällt.
Man erhält so gleichgroße Tropfen (Durchmesserschwankungen ≈ 10-5
[LIN 90a]
), die,
abhängig vom Vordruck, eine Anfangsgeschwindigkeit von etwa 10 - 30 m/s besitzen.
Mit dem Austritt des Flüssigkeitsstrahls in eine bekannte Atmosphäre beginnt der zu
untersuchende Prozeß.
ÜBERSICHT
77
Bild 4.1: Übersichtsskizze des experimentellen Aufbaus.
Zur Erzeugung des Raman-Spektrums wird der Strahl eines Ar+-Lasers (SpectraPhysics, Modell 2030-20, 514.5 nm, 2 - 8 W) auf die Tropfenkette fokussiert. Aus dem
Laserstrahl werden die Plasma-Linien herausgefiltert. Desweiteren ist die Polarisationsrichtung
einstellbar.
Der
Durchmesser
des
Laserstrahlfokusses
im
4. EXPERIMENTELLER AUFBAU
78
Untersuchungsvolumen wird durch die geeignete Wahl einer Linse oder eines
Achromaten vorgegeben.
Das Streulicht wird unter 90° zur Laserstrahl- und Tropfenfallrichtung von einem
Objektiv auf den Eintrittsspalt eines zweistufigen Spektrographen (Spex 1403)
projiziert. Ein holographisches Raman-Filter (Kaiser Optical Systems, HNF-514-1.0)
unterdrückt das elastische Streulicht der Laserstrahlung. Das Raman-Spektrum wird auf
die Austrittsebene des Spektrographen abgebildet. Dort befindet sich die Photokathode
eines Bildverstärkers (PCO, Modell IRO), der das Spektrum verstärkt und auf eine
flüssigstickstoffgekühlte CCD-Kamera (Wright Instr. 1) projiziert. Das von der CCDKamera detektierte Spektrum nimmt ein PC auf und wertet sie aus. Optional kann die
CCD-Kamera auch direkt in die Austrittsebene des Spektrographen gebracht werden,
wenn für bestimmte Versuche ein Bildverstärker nicht benötigt wird.
Der gesamte optomechanische Versuch ist auf einem selbstgebauten schwingungsisolierten Tisch aufgebaut. Dieser besteht im wesentlichen aus Mopedschläuchen,
Styroporschichten und einer Granit- / Stahlplatte, die auf einer Schicht Quarzsand liegt.
DIE ERZEUGUNG DER TROPFENKETTE
79
4.2 Die Erzeugung einer Kette von Mikrotropfen
Einführung, Theorie
Die Tropfenbildung wurde erstmals in der wissenschaftlichen Literatur 1686 von
Mariotte
[MAR 86]
erwähnt. Er machte das Fallen der Flüssigkeit im Schwerefeld für die
Bildung von Tropfen verantwortlich. Ein in eine Flüssigkeit fallender Tropfen löst
jedoch eine Fontäne aus, aus der sich auch entgegen der Schwerkraft Tropfen ablösen.
Plateau [PLA 49] zeigte 1849, daß die „treibende Kraft“ beim Abschnüren eines Tropfens
die Oberflächenspannung ist. Sie bewirkt eine Verkleinerung der Oberfläche, da es für
ein Flüssigkeitsmolekül energetisch günstiger ist, von gleichartigen Molekülen umgeben
zu sein, statt an Vakuum oder Gas anzugrenzen. Stellt man sich einen zylindrischen
Flüssigkeitsstrahl vor, der durch eine Blende tritt, so ist die Oberfläche der sich
bildenden
kugelförmigen
Tropfen
dann
kleiner
als
die
des
zylindrischen
Flüssigkeitsstrahls desselben Volumens, wenn [EGG 97]
dt >
3
2
ds
(4.1)
(dt: Tropfendurchmesser, ds: Durchmesser des Flüssigkeitsstrahls) gilt. Mit anderen
Worten, die Tropfen werden immer mindestens eineinhalb mal so groß wie der
Blendendurchmesser.
Die Größe der Tropfen ist allerdings begrenzt. Je größer die Tropfen, desto größer
werden auch die zu überwindenden Trägheitskräfte zu ihrer Bildung. Es gibt daher eine
optimale Tropfengröße, die der am schnellsten anwachsenden Störung auf der
Zylinderoberfläche entspricht. Bei realen Blenden oder Düsen werden kleine Störungen
jeder Wellenlänge auf dem Strahl erzeugt und diejenige Störung, die am schnellsten
anwächst, bestimmt die Größe des entstehenden Tropfens. Bei Annahme von kleinen
sinusförmigen Störungen auf dem Flüssigkeitszylinder zeigte Lord Rayleigh 1878
[RAY 78]
, daß die optimale Wellenlänge (Abstand zwischen zwei Einschnürungen)
4. EXPERIMENTELLER AUFBAU
80
λ opt ≈ 4.5 d s
(4.2)
beträgt. Die minimale Wellenlänge für den regelmäßigen Zerfall des Strahls wird mit
λ min = π d s
(4.3)
angegeben. Der Wellenlängenbereich zur Erzeugung von monodispersen Tropfen wurde
von Schneider und Hendricks [SCH 64] experimentell ermittelt:
35
. d s < λ opt < 7 d s .
(4.4)
Wird die Störwellenlänge λ mit der Frequenz
f =
vs
λ
(4.5)
induziert und drückt man die Geschwindigkeit des Flüssigkeitsstrahls vs durch den
Volumenstrom V& aus (Kontinuitätsgleichung: V& = vA = v s ⋅ π( d s / 2 )2 ), so erhält man
die Anregungsfrequenz f in Abhängigkeit zur Störwellenlänge und zum Volumenstrom:
f =
4 V&
.
π ds2 λ
(4.6)
Ist die Tropfenerzeugungsrate gleich der Anregungsfrequenz, so erhält man aus der
Massenerhaltung den Tropfendurchmesser
dt =
3
6 V&
π f
=
3
&
6 m
π f ρ
,
(4.7)
& der Massenstrom ist.
wobei ρ die Dichte der Flüssigkeit und m
Eine Zusammenstellung der Größenbereiche für die Störwellenlänge, die Anregungsfrequenz und den Tropfendurchmesser ist in Tab. 4.1 gegeben.
Es kann gezeigt werden, daß sich aus dem Gleichgewicht von Oberflächen- und
Trägheitskräften die Zeitskala, auf der es zur Entstehung von Tropfen kommt, bilden
läßt [EGG 97]:
DIE ERZEUGUNG DER TROPFENKETTE
81
Tabelle 4.1: Zusammenstellung der Größenbereiche für die Störwellenlänge, die
Anregungsfrequenz und den Tropfendurchmesser.
Störwellenlänge λ
Anregungsfrequenz f
t =
8 γ
opt.
max.
π ds
4.5 ds
7 ds
0.4
Tropfendurchmesser dt
d s3 ρ
min.
V&
d s3
1.68 ds
0.283
V&
d s3
1.89 ds
,
0.18
V&
d s3
2.19 ds
(4.8)
mit der Oberflächenspannung γ.
Nimmt man an, daß sich der Flüssigkeitsstrahl nicht zusammenzieht, wenn er die
Blende verläßt, dann erhält man über die Kontinuitätsgleichung aus dem
Volumenstrom V& die Anfangsgeschwindigkeit
v0 =
4 V&
π d s2
(4.9)
der Tropfen.
Weisen zu untersuchende Flüssigkeiten eine hohe Viskosität auf, wird der Zerfall des
Flüssigkeitsstrahls verlangsamt. In solchen Fällen wird der Flüssigkeit ein
leichtflüchtiges Lösungsmittel zugesetzt, um die Viskosität zu verringern. Ist das
Lösungsmittel verdunstet, haben die Partikel den Durchmesser
dp =
3
C dt
(4.10)
mit dem Mischungsverhältnis C zwischen dem Flüssigkeitsvolumen und dem
Gesamtvolumen des Gemisches. Gl. 4.10 läßt sich auch anwenden, wenn durch
4. EXPERIMENTELLER AUFBAU
82
Verdunstung eines Lösungsmittel/Salz-Gemisches feste Salzpartikel erzeugt werden
sollen. In diesem Fall ist C das Verhältnis aus der Massenkonzentration (Einheit:
kgSalz/m3Partikel) des Salzes und der Dichte (Einheit: kgSalz/m3Salz) des Salzpartikels
(C = cSalz/ρSalz) [VEH 98].
Weitere theoretische Betrachtungen über die nichtlineare Dynamik des Strahlzerfalls
findet man bei Eggers
[EGG 97]
. Dort wurde speziell der Abreißprozeß des Tropfens
simuliert und mit experimentellen Messungen verglichen. Eine Übersicht über die
Tropfenbildung in Hinsicht auf deren industrielle Anwendung, wie z.B. bei Sprayprozessen, lieferte Walzel [WAL 88].
Die bisherigen Betrachtungen gelten für idealisierte Bedingungen. Vorausgesetzt
wurden eine niedrige Viskosität der Flüssigkeit, kleine Störungen und die
Vernachlässigung
von
Umgebungseinflüssen.
Außerdem
wurde
von
einem
gleichmäßigen Strahlzerfall ausgegangen. Häufig entstehen jedoch zwischen zwei
Tropfen ein oder mehrere wesentlich kleinere sogenannte Satellitentropfen. Diese stören
meistens dann, wenn nur Tropfen einer Größe erwünscht sind. Zum Beispiel kann durch
Satellitentropfen die Druckqualität von Tintenstrahldruckern begrenzt werden [EGG 97].
Der Schwingblendengenerator
Der Flüssigkeitsstrahl kann in den von Tab. 4.1 angegebenen Bereichen kontrolliert
zerfallen, wenn ihm eine periodische Störung aufgeprägt wird. Dies kann durch
Druckschwankungen in der Flüssigkeit, Schallwellen oder eine schwingende
Austrittsblende realisiert werden. Besonders bewährt hat sich die schwingende
Austrittsblende. Nach diesem Prinzip funktioniert der von Berglund und Liu
[BER 73]
entwickelte Schwingblendengenerator (SBG)1, der später von der Firma TSI [TSI 82]
kommerziell vertrieben wurde. Bild 4.2 zeigt eine Skizze dieses Schwingblendengenerators. Er besteht im wesentlichen aus einer Abschlußkappe, auf der die ringförmige
Piezokeramik aufgeklebt ist und in der sich die Austrittsblende befindet. Die
1
Daher auch oft Berglund-Liu-Generator genannt. Die englische Bezeichnung ist vibrating orifice
aerosol generator (VAOG).
DIE ERZEUGUNG DER TROPFENKETTE
83
eingesetzten Austrittsblenden wurden kommerziell erworben [MEL 95] oder selbst gefertigt
[HOC 94]
. Soll ein monodisperses Spray erzeugt werden, so kann der Zerstäuberkappe
Zerstäubungsluft zugegeben werden. In der Bohrung der Zerstäuberkappe wird die
Tropfenkette verwirbelt und es entsteht ein turbulenter Freistahl.
Der von der Firma TSI vertriebene Schwingblendengenerator wurde von Lin et al.
[LIN 90a]
so modifiziert, daß Durchmesserschwankungen der Tropfen verringert wurden.
Lin et al. ersetzten die Spritzenpumpe durch ein Fördersystem, bei dem mittels eines
Gasballastes die Flüssigkeit gefördert wurde. Außerdem setzten sie einen stabileren
Frequenzgenerator ein und erreichten so eine relative Durchmesserschwankung von
2 ⋅ 10-5. Das in dieser Arbeit eingesetzte Versorgungssystem des Schwingblendengenerators ist dem ähnlich und wird in einem gesonderten Kapitel (Kap. 4.5.1, S. 106)
beschrieben.
Bild 4.2: Skizze des Schwingblendengenerators nach Berglund und Liu [BER 73].
4. EXPERIMENTELLER AUFBAU
84
Wie sich bei einigen Experimenten herausstellte
[VEH 95a]
, wird der Generatorkopf
nach Berglund und Liu beim Einsatz von korrosiven Gasen (z.B. SO2) beschädigt. Die
Piezokeramik und deren elektrische Kontaktierung liegen offen, so daß sie den
jeweiligen
Umgebungsbedingungen
ausgesetzt
sind.
Es
kommt
zu
Korrosionserscheinungen an den elektrischen Kontakten, den Klebestellen, die die
Piezokeramik fixieren, und an der Piezokeramik selbst. Weiterhin ist die Baubreite des
Generatorkopfes durch die geometrischen Abmessungen der Piezokeramik recht groß,
was zu ungünstigen Strömungsverhältnissen der Gasphase in der Nähe des
Partikelaustritts führen kann.
Daher wurde im Rahmen dieser Arbeit ein Schwingblendengenerator entwickelt, der
diese Probleme vermeidet. Die wesentliche Neuerung zeigt Bild 4.3: Die Austrittsöffnung des Schwingblendengenerators befindet sich am Ende eines Rüssels. Der Innendurchmesser des Rüssels ist begrenzt durch den Durchmesser des Blendenplättchens.
Die Länge des Rüssels ist beliebig und den gegebenen Anforderungen anpaßbar.
Innerhalb des Generators befindet sich eine Metallkapillare, durch die die zu
dispergierende Flüssigkeit zum Blendenplättchen geleitet wird. Soll der Generator zu
Reinigungszwecken gespült werden, so wird die Flüssigkeit durch die Kapillare bis zum
Blendenplättchen geführt, wo sich die Strömung umkehrt und die Flüssigkeit zwischen
der Kapillare und dem Rohr nach oben geleitet wird. Am oberen Ende des Rohres wird
die Flüssigkeit seitlich ausgeleitet. Wird der Generator in Betrieb genommen, wird
dieser Ausgang verschlossen. Im oberen Bereich des Generators befindet sich die
Auflage für die Piezokeramik, die mit einer elektrisch nichtleitenden Klemmscheibe
fixiert wird.
Optional kann über dem Rüssel eine Zerstäuberkappe angebracht werden, an deren
Ende sich eine Bohrung befindet, durch die die Tropfenkette geführt wird. Wird der
Zerstäuberkappe Zerstäubungsluft zugeführt, so wird die Tropfenkette in der Bohrung
verwirbelt und es entsteht auch hier ein turbulenter Freistahl (monodisperses Spray).
DIE ERZEUGUNG DER TROPFENKETTE
85
Bild 4.3: Modifizierter Schwingblendengenerator mit einem Strahlaustrittsrüssel.
Der schmale Rüssel erlaubt es, daß nur er in eine Meßkammer mit aggressiven
Umgebungsverhältnissen (z.B. korrosive Stoffe, hohe Temperaturen) eingeführt werden
muß, während die empfindlicheren Teile des Generators geschont werden. Außerdem
kann die Aerosolerzeugung beim Einsatz in geometrisch eng begrenzten Räumlichkeiten
besser positioniert werden. Weiterhin werden die Strömungsverhältnisse der Gasphase
durch die schmale Bauform des Rüssels weit weniger beeinflußt als bei den
herkömmlichen Generatoren. Das Profil des Rüssels kann so gestaltet werden, daß
aerodynamische Störungen durch den Rüssel minimiert werden. Der Durchmesser des
Rüssels kann weiter verringert werden, wenn Blendenplättchen mit einem kleineren
Außendurchmesser eingesetzt werden. Die Qualität der erzeugten Aerosole ist identisch
mit der der herkömmlichen Schwingblendengeneratoren.
4. EXPERIMENTELLER AUFBAU
86
Erfahrungen, Praxis
Der im theoretischen Teil beschriebene Strahlzerfall ist der Idealfall. Häufig hat man
jedoch Artefakte und Störungen, die berücksichtigt werden müssen. Schon erwähnt
wurden die Satellitentropfen, die zwischen zwei Tropfen entstehen können und die
wesentlich kleiner sind. Treten Satelliten auf, so verfälschen sie Meßergebnisse, wenn
man Tropfen derselben Größe angenommen hat. Der Stoffaustausch bei Desorptionsund Absoptionsprozessen vollzieht sich bei Satelliten schneller als bei den Tropfen.
Werden optische Resonanzen untersucht, überlagern sich die Resonanzen von Tropfen
und Satelliten. Soll die Gasphase zwischen den Tropfen optisch vermessen werden,
überstrahlt das Flüssigphasensignal der Satelliten das Gasphasensignal.
Die Stabilität einer monodispersen Tropfenkette, bezüglich des Abstandes zwischen
den Tropfen und bezüglich der Ausbreitungsrichtung der Tropfen, nimmt mit dem
Abstand zum Generator ab, bis sich ein Spray entwickelt hat. Die Länge, innerhalb der
die Tropfenkette eine regelmäßige Struktur besitzt, bezeichnet man als Kohärenzlänge
[AND 92]
. Sie hängt von den Umgebungsbedingungen (Druck, Temperatur), den
Betriebsparametern des Generators (Differenzdruck zwischen Flüssigkeit und Gasphase,
Blendendurchmesser, Flüssigkeitsmedium) und der Wechselwirkung zwischen dem
Flüssigkeitsmedium und der Gasphase ab. Bei Normalbedingungen (T=20°C, p=1 bar)
und einer geringen Wechselwirkung zwischen Gas- und Flüssigmedium beträgt die
Kohärenzlänge etwa 30 bis 150 mm. Bei zunehmender Wechselwirkung zwischen der
Gasphase und den Tropfen (z.B. Stoffaustausch) verkürzt sich die Kohärenzlänge. Fallen
die Tropfen in ein Vakuum, kann sich die Kohärenzlänge auf mehrere Meter verlängern
[ORM 90]
. Ein optischer Meßaufbau zur Untersuchung der Strahlstabilität wurde von
Lemken entwickelt
geplant.
[LEM 97]
. Eine systematische Untersuchung mit diesem Aufbau ist
DIE ERZEUGUNG DER TROPFENKETTE
87
Der Zerfall des Flüssigkeitsstrahls in Tropfen ist nach der dafür charakteristischen
Zerfallslänge [WEB 31] abgeschlossen. Sie hängt vom Flüssigkeitsmedium (Oberflächenspannung, Viskosität, Dichte), von dem Durchmesser, der Geschwindigkeit des Flüssigkeitsstrahls und von der Störamplitude ab. Diese kann durch die Spannung beeinflußt
werden,
mit
der
die
Piezokeramik
betrieben
wird.
Mit
einer
größeren
Wechselspannungsamplitude bewirkt man eine größere Störung und damit eine kürzere
Zerfallslänge. Weiterhin zeigt sich, daß eine angelegte Rechteckspannung den Strahl
besser zerfallen läßt als eine Sinusspannung.
Die Störamplitude wird weiterhin durch die mechanischen Eigenschaften der
Piezokeramik sowie des gesamten Generators samt Halterung beeinflußt. Bei
bestimmten Frequenzen zeigt eine Piezokeramik Resonanzen. Ist die Piezokeramik
mechanisch an andere Bauteile gekoppelt, so können sich die Resonanzfrequenzen
verschieben. Die Folge ist, daß ein Schwingblendengenerator nicht über den in Tab. 4.1
angegebenen Frequenzbereich gleich gut funktioniert. Es existieren immer nur recht
schmale Frequenzbereiche, innerhalb derer monodisperse Tropfenketten erzeugt werden
können.
Die Bedingungen zur Bereitstellung einer stabilen monodispersen Tropfenkette sind
also derart speziell, daß es notwendig ist, den einwandfreien Zustand der Tropfenkette
zu überprüfen.
Kontrolle der Tropfenkette
Zur Überprüfung der Tropfenkette eignet sich unter anderem das elastisch gestreute
Licht. Liegt eine monodisperse Tropfenkette vor, so entsteht ein Interferenzmuster aus
konzentrischen Ringen und horizontalen Streifen. Die Ringe entstehen durch die MieStreuung der Laserstrahlung an den kugelförmigen Tropfen und sind im ganzen Raum
um die Tropfen verteilt. Aus ihr läßt sich die Größe der Tropfen bestimmen [KOE 86].
4. EXPERIMENTELLER AUFBAU
88
In Vorwärtsrichtung ist die Mie-Streuung am intensivsten. Die Streifen entstehen,
wenn der Abstand zwischen den Tropfen konstant ist. In diesem Fall bildet die
Tropfenkette einen Mehrfachspalt oder ein Strichgitter, an dem die Laserstrahlung
gebeugt wird. Das Streifenmuster entsteht dann durch Interferenz. Der Abstand
zwischen den Streifen ist ein Maß für den Abstand zwischen den Tropfen. Aus dem
Tropfenabstand und der Anregungsfrequenz läßt sich die Tropfengeschwindigkeit
bestimmen
[MOO 95, DEV 98]
. Das Streifenmuster wird schärfer, je mehr Tropfen beleuchtet
werden. Gute Ergebisse erzielt man, wenn der Laserstrahl durch eine Zylinderlinse auf
die Tropfenkette fokussiert wird. Bild 4.4 zeigt ein so erstelltes Interferenzmuster. Ist
der Abstand zwischen den Tropfen nicht mehr konstant bzw. die Kohärenzlänge
überschritten, so wird das Bild der horizontalen Streifen unscharf oder verschwindet. In
Bild 4.4:
Interferenzmuster einer Tropfenkette. Der Strahl eines He-Ne-Lasers (30 mW)
wurde durch eine Zylinderlinse (f = 60 mm) auf die Ethanoltropfenkette
(Tropfendurchmesser
etwa
35 µm)
Interferenzmuster photographiert.
fokussiert
und
das
entstehende
DIE ERZEUGUNG DER TROPFENKETTE
89
einem solchen Fall kann die Tropfenkette immer noch monodispers sein, so daß die
konzentrischen Ringe erhalten bleiben. Existierten Satellitentropfen, so überlagern sich
mehrere Interferenzmuster. Nimmt der Grad der Monodispersität der Tropfenkette ab,
wird das gesamte Interferenzmuster verschwommener, bis sich keine Strukturen mehr
erkennen lassen.
Eine weitere Methode zur Überprüfung der Tropfenkette ist die stroboskopische
Mikroskopie durch den „Tropfenkettenmonitor“ [KUE 98]. Die Tropfenkette wird durch ein
in die Horizontale gebrachtes Mikroskop beobachtet. Als Lichtquelle dient eine LED,
die sich auf der optischen Achse des Mikroskops befindet. Die LED wird mit der
Anregungsfrequenz der Tropfenerzeugung gepulst betrieben. Um ein scharfes stehendes
Bild der Tropfenkette zu bekommen, wurde eine Pulszeit von etwa 200 ns gewählt. Die
Beobachtung der Tropfenkette geschieht durch eine CCD-/Videokamera, einen Fotoapparat oder durch das Auge (eine detaillierte Beschreibung ist in Kap. 4.5.3 zu finden,
S. 119). Damit läßt sich der Zerfall des Flüssigkeitsstrahls, die etwaige Größe und
Position der Satellitentropfen zwischen den Tropfen und eventuelle Nichtsphäridizitäten
(Oblaten, Prolaten) der Tropfen (z.B. am Anfang der Tropfenkette) beobachten.
Der Zerfall des Flüssigkeitsstrahls kann durch Messung der Tropfenladung
beobachtet werden
[REI 77,VEH 97]
. Bis zum Zerfall des Strahls in Tropfen liegt eine
„Flüssigkeitsspitze“ vor. Am Ende der Spitze können sich Ladungsträger (Elektronen)
sammeln, so daß hohe elektrische Felder auftreten (Spitzeneffekt, -wirkung), wenn in
Richtung der Spitze ein positives elektrisches Potential aufgebaut wird. Mit anderen
Worten, die Elektronen werden zum Ende des Flüssigkeitsstrahls gezogen, so daß der
nächste sich ablösende Tropfen elektrisch (induktiv) aufgeladen ist. Zerfällt der
Flüssigkeitsstrahl optimal, so ist die Flüssigkeitsspitze kurz, der Spitzeneffekt nicht so
ausgeprägt und die Tropfen weniger aufgeladen und umgekehrt. Durch Messung der
Tropfenladung können also die Betriebsbedingungen für den optimalen Strahlzerfall
ermittelt werden. Experimentell erreicht man dies, indem die Zerstäuberkappe (siehe
Bild 4.2 und 4.3) durch eine Kupferelektrode ersetzt wird, die vom Generator elektrisch
isoliert ist. An die Elektrode wird eine positive Spannung (bis zu 50 V) angelegt. Die
90
4. EXPERIMENTELLER AUFBAU
aufgeladenen Tropfen fallen, wie bei der Zerstäuberkappe, durch die Mittelbohrung. Um
die Ladung der Tropfen zu messen, werden sie von einem Faradaybecher gesammelt.
Die Ladungen können über den Faradaybecher abfließen und werden von einem
Elektrometer registriert.
OPTISCHER AUFBAU
91
4.3 Der optische Aufbau
In diesem Kapitel werden die wesentlichen experimentellen Komponenten der
optischen Anregung und Detektion beschrieben.
4.3.1 Die Anregung zur Raman-Streuung
Zur Anregung der Raman-Streuung wird der Strahl eines Argonionenlasers (SpectraPhysics, Modell 2030-20) eingesetzt. Der Laser wird meistens im single-line-mode auf
seiner grünen Linie (λ = 514.53 nm) betrieben. Bei Messungen werden Leistungen
zwischen 2 und 10 W gewählt. Im light-control-mode wird die Stabilität der Laserleistung mit ± 0.5 % spezifiziert [SPE 87]. In Bild 4.1 ist unter anderem auch der Strahlengang skizziert. Der Laserstrahl wird zuerst durch einen Spiegel auf ein Plasmalinienfilter
[GRO 97]
gelenkt. Dieses besteht im wesentlichen aus einem Prisma, welches die gesamte
Plasmalinienemission der Laserröhre spektral zerlegt. Kurz vor dem Untersuchungsvolumen befindet sich eine Blende, die alle Plasmalinien abblockt, bis auf den
Laserstrahl.
Nach
dem
Plasmalinienfilter
passiert
der
Laserstrahl
einen
Polarisationsdreher (Spectra-Physics, Modell 310-21), der so eingestellt ist, daß die
Polarisationsrichtung des Laserstrahls im Untersuchungsvolumen senkrecht zur
Beobachtungsrichtung steht (90°-Geometrie). Drei weitere Spiegel lenken den
Laserstrahl in das Untersuchungsvolumen. Ein Achromat (Linse) fokussiert den
Laserstrahl. Es werden verschiedene Achromate mit Brennweiten zwischen 25 und
150 mm eingesetzt. Bedingt durch Transmissions- und Reflexionsverluste der optischen
Bauteile beträgt die Leistung im Untersuchungsvolumen nur etwa 50 - 60% von der
Ausgangsleistung. Eine Zusammenstellung der wichtigsten Kenngrößen findet sich in
Tab. 4.2.
4. EXPERIMENTELLER AUFBAU
92
Tabelle 4.2: Die wichtigsten Kenngrößen des Argonionenlasers [SPE 87] .
Hersteller und Vertreiber
Spectra-Pysics
Modell
2030-20
Strahldurchmesser
(bei 514.5 nm, TEM00, 1/e2)
1.8 mm
Strahldivergenz (bei 514.5 nm)
0.45 mrad
maximale Leistung (bei 514.5 nm)
10 W
Leistungsstabilität (innerhalb 30 min)
± 0.5%
Resonatorlänge
1.78 m
Polarisationsverhältnis (vertikal)
> 100 : 1
4.3.2 Die Detektionseinheit
Das aus dem Untersuchungsvolumen gestreute Licht wird unter einem Streuwinkel
von etwa 90° und senkrecht zur Polarisationsrichtung des einfallenden Laserstrahls von
einem Kameraobjektiv (Canon, FD 85 mm 1:1,2) gesammelt und über zwei Spiegel auf
den Eintrittsspalt eines zweistufigen Spektrographens abgebildet (siehe Bild 4.1). Der
Öffnungswinkel beträgt etwa 37° und der Abbildungsmaßstab ist 9.1 : 1.
Der Spektrograph
Bei dem Spektrographen handelt es sich um einen zweistufigen Czerny-TurnerMonochromator (Spex 1403). In jeder Stufe ist ein Gitter mit je 600 Linien/mm
eingebaut, so daß eine lineare Dispersion von ≈ 30 cm-1/mm erreicht wird. Die
Mittelspalte werden auf etwa 10 mm geöffnet und fixiert. Die wichtigsten Kenngrößen
sind in Tab. 4.3 zusammengefaßt. Zwischen den Mittelspalten wird ein holographisches
Raman-Filter (POC, RHE 514.1D)
[YAN 91]
eingebaut, um das elastisch gestreute Licht
nochmals zu reduzieren. Der Austrittsspalt wird entfernt, um in der Austrittsebene eine
zweidimensionale Detektionseinheit anzubringen. Dabei werden für diese Arbeit zwei
OPTISCHER AUFBAU
93
Tabelle 4.3: Die wichtigsten Kenndaten des Spektrographens [SPE 81].
Hersteller und Vertreiber
Spex Industries
Modell
1403
Anordnung
Czerny-Turner,
additive Dispersion
fokale Länge
0.85 m
Öffnungsverhältnis
f / 7.8
Gitter
600 Linien/mm,
Blazewellenlänge: 500 nm
30 cm-1
Lineare Dispersion (bei 514.5 nm)
± 0.2 cm-1
Reproduzierbarkeit
≈ 10 mm, fixiert
Mittenspalte
Anordnungen eingesetzt. Zum einen wird eine CCD-Kamera direkt in die Austrittsebene
gebracht. Damit werden Messungen durchgeführt, bei denen eine gepulste Detektion
nicht nötig ist, wie z.B. die Messung von Spektren an einer Küvette. Andererseits wird
für eine gepulste Detektion in die Austrittsebene ein Bildverstärker angebracht und das
verstärkte Licht auf die CCD-Kamera abgebildet. Eine genauere Beschreibung des
Bildverstärkers wird im nächsten Abschnitt geliefert.
Die CCD-Kamera
Bei der CCD-Kamera (Wright Instruments, Nr. 1)
[BAR 77]
handelt es sich um einen
rechteckigen CCD-Sensor, der zur Unterdrückung des Dunkelstroms mit flüssigem
Stickstoff gekühlt wird. Der Sensor hat ein Format von 385 × 578 Pixeln, bzw.
8.5 × 12.8 mm. Die Kantenlänge der quadratischen Pixel beträgt 22 µm. Eine
Zusammenstellung der wichtigsten Kenngrößen für die CCD-Kamera ist in Tab. 4.4 zu
finden.
4. EXPERIMENTELLER AUFBAU
94
Tabelle 4.4: Die wichtigsten Kenndaten der CCD-Kamera.
Hersteller
Wright Instruments
Vertreiber
DILOR GmbH
Modell
Nr. 1
Betriebstemperatur
150 K, fl. Stickstoff gekühlt
CCD-Chip
EEV P8603SB
385 × 578
Anzahl der Pixel
Pixelgröße
22 µm
Quantenausbeute (bei 650 nm)
39 %
4.3.3 Der Bildverstärker
Übersicht
Ein wesentliches Bauteil des Versuchsstandes ist der Bildverstärker (BV, auch
Restlichtverstärker). Daher soll er hier etwas eingehender beschrieben werden. Ein BV
besteht im wesentlichen aus einer Photokathode, einer Mikrokanalplatte (microchannel
plate, MCP) und einem Phosphorschirm. Auf der Photokathode werden die
auftreffenden Photonen in Elektronen konvertiert. Diese werden in der MCP durch
Sekundärelektronenemission vervielfacht und auf den Phosphorschirm beschleunigt.
Auf dem Phosphorschirm lösen die Photoelektronen ein Phosphoreszenzleuchten aus.
Ein Bild, das auf die Photokathode abgebildet wird, wird auf dem Phosphorschirm
verstärkt wiedergegeben. Das verstärkte Bild wird nun auf die CCD-Kamera projiziert
und detektiert.
Die meisten Anwendungsmöglichkeiten
Eigenschaften
des
BV
begründet:
[WOO 71, HAM oJ]
Erstens
wird
sind durch die wichtigsten
die
Empfindlichkeit
der
5
Detektionseinheit erhöht (Verstärkungsfaktoren bis 10 sind möglich) und zweitens kann
durch Schalten der Spannung an der Photokathode der BV an- und ausgeschaltet
OPTISCHER AUFBAU
95
werden. Da dies elektronisch erfolgt, können Verschlußzeiten (gates) von einigen
Nanosekunden erreicht werden [PCO 90].
Die eingesetzte Bildverstärkereinheit (PCO Computer Optics, Modell IRO) besteht
aus einem Bildverstärkerkopf und einem Steuergerät (PCO, Modell DiDEC). In dem
Bildverstärkerkopf befindet sich die Bildverstärkerröhre (Hamamatsu, Modell V3347U proximity focused image intensifire tube; bestehend aus der Photokathode, der MCP
und dem Phosphorschirm) sowie ein Hochspannungsmodul (PCO, Modell HVMCP),
zwei Pulsermodule (PCO, Modelle HVP2N und HVP5N) und zwei Linsen für die
Tandemoptik. Mit einem Kameraadapter kann an den Bildverstärkerkopf (im Folgenden
der Einfachheit halber weiterhin BV bezeichnet) ein Kameraobjektiv montiert werden.
Im Verlauf der Arbeit werden zwei Objektive eingesetzt (Nikon F1.2 / 50 mm und CMount F1.3 / 75 mm), die verschiedene Abbildungsmaßstäbe liefern. Ein BlockDiagramm der Bildverstärkereinheit zeigt Bild 4.5. Die wichtigsten Kenngrößen der
Bildverstärkereinheit sind in Tab. 4.5 am Ende dieses Kapitels zusammengefaßt.
Der BV wurde so an den Spektrographen montiert, daß die Photokathode in der
Bild 4.5:
Blockdiagramm der Bildverstärkereinheit [PCO 93a].
4. EXPERIMENTELLER AUFBAU
96
Austrittsebene des Spektrographen lag. Das Bild der Austrittsebene wurde nun durch
den BV verstärkt und durch eine Optik (Kollimator Objektiv, Rodenstock,
F1.4 / 100 mm; verschiedene Ausgangsobjektive) auf die CCD-Kamera abgebildet.
Beschreibung der Einzelkomponenten
Eine Übersicht über die wesentlichen Einzelkomponenten des BV zeigt Bild 4.6. Dort
wird der Spektrograph durch eine Abbildungsoptik vereinfacht dargestellt.
Trifft Licht auf die Photokathode, so werden durch den äußeren Photoeffekt
Photoelektronen freigesetzt. Die Photokathode besteht aus einer dünnen Schicht eines
Materials (V3347U: Multialkali
[HAM 92]
) mit niedriger Austrittsenergie für die
Elektronen. Durch die Wahl von Material und Schichtdicke kann die spektrale
Empfindlichkeit vom ultravioletten bis zum nahen infraroten Spektralbereich variiert
werden. Die Quantenausbeute liegt bei vielen Materialien bei etwa 10 - 20 %. Durch die
Wahl der Spannung, die an die Photokathode gelegt wird, können die Elektronen auf die
MCP hin beschleunigt (negative Spannung) oder von der Photokathode festgehalten
(positive Spannung) werden. Dadurch kann der BV als elektronischer Verschluß mit
einem Verschlußzeitverhältnis von etwa 1 : 107 genutzt werden. Mit einem
leistungsfähigen Hochspannungspulsgenerator (z.B. HVP5N) werden Anstiegszeiten
von einigen Nanosekunden erreicht. Bei Gate-Zeiten von ∆t > 100 ns kann der
sogenannte „Iriseffekt“1 ausgeschlossen werden.
Die Vervielfachung der Photoelektronen erfolgt in der MCP. Die eingesetzte MCP ist
aus Bleiglas gefertigt und beinhaltet etwa 106 - 107 Kanäle mit einem typischen
Durchmesser von 10 µm und einer Länge von ca. 0.5 mm. Zwischen dem Ein- und dem
Austritt eines jeden Kanals wird eine Spannung angelegt, so daß die Elektronen in
Richtung der Austrittsöffnung beschleunigt werden.
1
Der „Iriseffekt“ kommt zustande, wenn beim Einschalten der Spannung der Bildverstärker zuerst
außen öffnet, da sich das angelegte elektrische Potential ausgehend vom Rand bis in die Mitte hin
ausbreitet. Der offene Bereich breitet sich dann zum Inneren hin aus. Der Ausschaltvorgang zeigt dagegen
das invertierte Verhalten. Bei sehr kurzen Verschlußzeiten führt dieser Effekt dazu, daß im inneren
Bereich nicht geöffnet wird oder eine radiale Abhängigkeit der Verstärkung auftritt.
OPTISCHER AUFBAU
Bild 4.6:
97
Die Einzelkomponenten des Bildverstärkers und deren elektrische Anschlüsse
[PCO 90]
. Der Spektrograph ist durch die Abbildungsoptik vereinfacht dargestellt.
Trifft
ein
Elektron
auf
die
Innenwand
eines
Kanals,
so
werden
dort
Sekundärelektronen erzeugt, die nach einer kurzen Wegstrecke wieder auf die Wand
treffen und dort weitere Sekundärelektronen erzeugen. Jeder Kanal stellt daher einen
Photomultiplier dar, bei dem die Dynoden durch eine einzige halbleitende Oberfläche
ersetzt sind. Der Verstärkungsgrad hängt von dem Verhältnis Länge zu Durchmesser der
Kanäle und von der angelegten Spannung ab. Die Lichtverstärkung des BV ist damit
allein durch die angelegte Beschleunigungsspannung variierbar und liegt zwischen 0 und
etwa 104 [HAM 92]. Bei einer hohen Beleuchtung des BV tritt in den Kanälen der MCP ein
Sättigungseffekt auf, der die erreichbare Verstärkung reduziert. Zu hohe Beleuchtungen
können zur Zerstörung oder zu lokalen Einbrennvorgängen innerhalb des BV führen.
Die aus der MCP austretenden Sekundärelektronen werden schließlich durch eine
Spannung von einigen Kilovolt auf den Phosphorschirm beschleunigt und regen diesen
zum Leuchten an. Das Phosphormaterial P20 leuchtet grün-gelb (λ ≈ 400 - 700 nm,
λmax ≈ 530 nm) mit einer Nachleuchtdauer von 0.01 bis 4 ms (abhängig vom
eingestrahlten Puls) [HAM 92]. Der Wirkungsgrad des Phosphorschirms beträgt etwa 20 %.
4. EXPERIMENTELLER AUFBAU
98
Die gesamte Einheit Photokathode-MCP-Phosphorschirm ist in Glas eingeschweißt
und befindet sich im Vakuum (10-6 mbar), um Wechselwirkungen der Elektronen mit
den Gasatomen zu vermeiden. Trifft dennoch ein Elektron ein Gasatom, so entsteht ein
positives Ion, das auf die Photokathode hin beschleunigt wird und dort störende
Elektronen auslöst (Ion-feedback).
Bei dem eingesetzten BV handelt es sich um einen Nahfokus-BV (proximity focused
image intensifier), dessen Funktionsweise oben beschrieben wurde. Eine andere
Konstruktion stellt der Inverter-BV (inverter type image intensifier) dar, bei dem die von
der Photokathode kommenden Elektronen durch Elektroden (Elektronenlinsen) auf die
MCP abgebildet werden [HAM 92].
Zur optischen Kopplung von Phosphorschirm und CCD-Kamera wird ein
Abbildungssystem aus Linsen (Kollimator Objektiv, Rodenstock, F1.4 / 100 mm;
verschiedene Ausgangsobjektive) gewählt. Man erhält damit verzerrungs- und
bildfehlerarme Abbildungen, die außerdem einen frei wählbaren Abbildungsmaßstab
ermöglichen. Nachteilig wirkt sich der relativ kleine Wirkungsgrad von 10 - 20 % und
ein aufwendiger mechanischer Aufbau aus. Will man die Verluste verringern, so eignet
sich zur Kopplung eine Glasfiberplatte (Taper, Faseroptik). Sie besteht aus vielen
Lichtleitfasern mit einem Durchmesser von einigen Mikrometern, die miteinander zu
einem Strang verschweißt sind.
An der Kontrolleinheit DiDEC wird die Belichtungspulslänge (width), in der der BV
auf Transmission geschaltet wird, die Zeitverzögerung (delay) des Belichtungspulses,
die Verstärkung (gain) durch die MCP und der Hochspannungspulser (HVP2N oder
HVP5N) eingestellt. Getriggert wird die Kontrolleinheit durch TTL-Pulse. Wird eine
2 m lange Zuleitung zwischen der Kontrolleinheit und dem BV eingesetzt, so muß eine
systembedingte Zeitverzögerung von 60 ns berücksichtigt werden.
OPTISCHER AUFBAU
99
Tabelle 4.5: Die wichtigsten Kenndaten der Bildverstärkereinheit [PCO 93].
Gesamtsystem:
Vertreiber
Modell
Bildverstärkerröhre:
Vertreiber
Modell
Durchmesser
Spektraler Bereich
max. Empfindlichkeit bei
Mikrokanalplatte (MCP)
gatebar
Photokathode
Spannung
Eingangsfenster
Phosphorschirm
Spannung
Hochspannungspulsmodule:
Vertreiber
Modell 1 / 2
min. Pulsbreite
Anstiegs-, Abfallzeit
max. Pulsfrequenz
Optik:
Kollimator Objektiv:
Vertreiber
Blendenzahl / Brennweite
Ausgangsobjektive:
1. Vertreiber
Blendenzahl / Brennweite
Abbildungsmaßstab
2. Typ
Blendenzahl / Brennweite
Abbildungsmaßstab
Kontrolleinheit:
Vertreiber
Modell
Belichtungszeit (width)
Verzögerungszeit (delay)
System-Delay (bei 2 m Zuleitung)
Verstärkung (durch MCP; gain)
PCO Computer Optics
IRO - Intensified Relais Optik
Hamamatsu
V3347U
25 mm
180 - 800 nm
430 nm
MCP „proximity focused“
ab 5 ns (fast gate)
S20
ein: -180 V; aus: +80 V
Quarz
P20
6 - 7 kV (intern eingestellt)
PCO Computer Optics
HVP2N / HVP5N
100 ns / 5 ns
25 ns / 2 ns
200 kHz / 2 kHz
Rodenstock
1.4 / 100 mm
Nikon
1.2 / 50 mm
1:2
C-Mount (für CCD-Video-Kameras)
1.3 / 75 mm
1 : 1.3
PCO Computer Optics
DiDEC
min.: 5 ns; max.: 1 ms
min.: 0 ns; max.: 1 ms
60 ns
0 - 10 (entspr. 0 - 900 V a.d. MCP)
100
4. EXPERIMENTELLER AUFBAU
4. EXPERIMENTELLER AUFBAU
100
4.4 Meßdatenerfassung und Auswertung
4.4.1 Hard- und Software
Der Spektrograph (Spex 1402) konnte manuell von einem Keyboard (Spex
Compudrive CD2) aus gesteuert werden. In den meisten Fällen wurde das Keyboard
jedoch von einem Steuerrechner (Epson PC, 386DX) über eine RS 232-Schnittstelle
fernbedient. Mit dem Steuerrechner wurde nicht nur der Spektrograph bedient, sondern
auch die CCD-Kamera. Die Software dazu wurde von dem Hersteller der CCD-Kamera
geliefert (Wright Instr., AT1 Vers. 3.01). Signale, die von der CCD-Kamera detektiert
wurden, wurden von dem Programm AT1 erfaßt und auf dem Steuerrechner im FITSFormat [WEL 81] gespeichert. Die Auswertung der Signaldaten konnte in einem begrenzten
Maße ebenfalls von dem Programm AT1 durchgeführt werden. Meistens wurden die
Daten jedoch von anderer Software auf anderen Rechnern (i. allg. PCs des Typs
486DX33), die über ein Netzwerk (Novell Netware, Vers. 3.11) verbunden waren,
ausgewertet. Dazu wurden die Daten mit dem Programm KONVERT.EXE (Fortran)
zunächst vom FITS-Format in das ASCII-Format konvertiert. Die Software, die dies
leistete, wurde selbst entwickelt [KOL oJ]. Dreidimensionale Datensätze (Intensitätsverteilung über einer Fläche), bei denen der gesamte CCD-Chip oder Teile davon
ausgelesen wurden, wurden von dem Programm AT12P3D.EXE (Fortran) konvertiert.
Die dabei entstandenen ASCII-Dateien enthielten die dreidimensionale Information in
dem Format P3D. P3D-Dateien konnten mit dem Programm P3D2BMP.EXE (Fortran)
in ein bitmap-Format konvertiert werden.
Zur
Bestimmung
des
Massenstroms
der
Flüssigkeit,
die
der
Schwingblendengenerator abgibt, wurde der Flüssigkeitsvorratsbehälter über einen
bestimmten Zeitraum gewogen (Sartorius, Modell LC 3200 D). Die Waage wurde in
wählbaren Zeitabständen über eine RS 232-Schnittstelle von einem PC (286XT18) mit
dem Programm WAAGE.EXE (Basic) ausgelesen.
MEßDATENERFASSUNG UND AUSWERTUNG
101
Für die Aufnahme von Meßwerten von einem Oszilloskop (Philips, Modell PM 3394)
stand das Programm PM3394.EXE (Basic) zur Verfügung. Damit wurden beispielsweise
die Photodiodensignale zur Geschwindigkeitsmessung der Tropfen (siehe Kap. 4.5.2)
aus dem Speicher des Oszilloskops ausgelesen.
Zur Auswertung jedweder Meßdaten wurden problemspezifische Programme (Pascal)
entwickelt, die in den jeweiligen Kapiteln beschrieben werden. Die Darstellung und
Präsentation von Ergebnissen wurde mit kommerziell erworbener Software durchgeführt
(MicroCal ORIGIN, Vers. 3.5 und 4.1; MS EXCEL, Vers. 4.0; MS Word für Windows,
Vers. 2.0b und 6.0c; CorelDRAW, Vers. 3.0; Paint Shop Pro, Vers. 3.0).
4.4.2 Die zweidimensionale Spektroskopie
Wie in Kapitel 4.3.2 (S. 92f) ausgeführt, wurde der Austrittsspalt des Monochromators entfernt, so daß ein Teil der Austrittsebene detektiert werden konnte. Damit
wurde aus dem Monochromator ein Spektrograph, da nicht nur „eine Farbe“
(monochrom) detektiert wird, sondern ein auf die Austrittsebene abgebildeter spektraler
Bereich (Bild 4.7). Dabei wird eine spektrale Auflösung entlang der Horizontalen
erreicht, entsprechend der senkrechten Anordnung des Eintrittsspalts und der
Gitterstriche. Ist eine Substanz gleichmäßig im Beobachtungsvolumen verteilt, so erhält
man in der Austrittsebene senkrechte Linien des Streuspektrums. Entlang des
Eintrittsspalts (bzw. der Gitterstriche) wird keine spektrale Auflösung erzielt. In dieser
Richtung erhält man eine räumliche Auflösung entlang des Beobachtungsvolumens, das
auf den Eintrittsspalt abgebildet wird. Entlang einer Linie des Streuspektrums läßt sich
damit
eine
Ortsinformation
aus
dem
Beobachtungsvolumen
gewinnen.
Das
Beobachtungsvolumen ist meistens ein Ausschnitt aus dem fokussierten Laserstrahl.
Die von der CCD-Kamera detektierte Intensitätsverteilung der Austrittsebene kann
unterschiedlich ausgewertet werden. Wie in Bild 4.7 skizziert, erhält man ein Spektrum,
wenn die horizontalen Zeilen des CCD-Signals zusammengefaßt werden (binning1).
1
Unter einem „binning“ versteht man das Zusammenfassen der Ladungen (Signale) mehrerer CCD-
Pixel, wobei noch durch die Anzahl der Pixel geteilt wird. Werden benachbarte Pixel zusammengefaßt,
erhöht sich das Signal-Rausch-Verhältnis mit einer einhergehenden Einbuße der Auflösung. Bei der
4. EXPERIMENTELLER AUFBAU
102
Bild 4.7:
Skizze zur abbildenden oder zweidimensionalen Spektroskopie.
Werden die vertikalen Spalten zusammengefaßt, bekommt man eine lokale Information
entlang des Untersuchungsvolumens. In beiden Fällen erhält man nur die
rauschreduzierten
Informationen
eines
Typs
(entweder
spektral
oder
lokal;
eindimensionale Spektroskopie) mit dem Verlust der Informationen des anderen Typs.
Zusammenfassung aller CCD-Pixel-Zeilen, so daß ein Spektrum wie von einem Zeilendetektor (z.B.
einem OMA-System) entsteht, verschwindet die Ortsauflösung ganz.
MEßDATENERFASSUNG UND AUSWERTUNG
Bild 4.8:
103
Logarithmische, invertierte Graustufendarstellung der zweidimensionalen
Intensitätsverteilung eines Raman-Signals auf dem CCD-Sensor. Horizontal
erhält man eine spektrale Auflösung, vertikal die örtliche Auflösung entlang
des anregenden Laserstrahls (links) sowie senkrecht zur Tropfenkette. Die
Tropfenkette verläuft in dieser Darstellung in die Zeichenebene durch den
Laserstrahl. Das Flüssigphasensignal der Tropfenkette verläuft daher in der
Bildmitte von links nach rechts als schmales Band. Ober- und unterhalb davon
wird nur das Gasphasensignal in der Nähe der Tropfenkette detektiert. Die
örtlichen Abmessungen senkrecht zur Tropfenkette sind hier etwa ±1 mm.
4. EXPERIMENTELLER AUFBAU
104
Sollen die spektralen und lokalen Informationen erhalten bleiben, muß das gesamte
Bild des CCD-Sensors ausgewertet werden (abbildende oder zweidimensionale
Spektroskopie). Dazu wird das Bild in Zeilen (oder Spalten) aufgespaltet und jede Zeile
(oder Spalte) einzeln ausgewertet (siehe Kap. 5.2, S. 136ff).
Bild 4.8 zeigt eine logarithmische, invertierte Graustufendarstellung der Intensitätsverteilung auf dem CCD-Sensor. Untersucht wird der Desorptionsprozeß von Acetylen
aus Acetontropfen an der Tropfenkette [MOR 96a]. Nach dem Austritt der Tropfen aus dem
Schwingblendengenerator beträgt die Konzentration des Acetylens 0.96 mol/l und die
Geschwindigkeit der 48 µm großen Tropfen etwa 20 m/s. Gemessen wird 10 mm
unterhalb des Generators. In vertikaler Richtung erhält man die örtliche Auflösung
entlang des anregenden Laserstrahls. Die Tropfenkette verläuft in dieser Darstellung in
die Zeichenebene durch den Laserstrahl. Das Flüssigphasensignal der Tropfenkette
verläuft daher in der Bildmitte von links nach rechts als schmales Band. Ober- und
unterhalb davon wird nur das Gasphasensignal in der Nähe der Tropfenkette detektiert.
Die örtlichen Abmessungen senkrecht zur Tropfenkette betragen hier etwa ±1 mm. In
horizontaler Richtung erhält man die spektrale Auflösung, entsprechend des
darunterliegenden Spektrums.
Auf der linken Seite der Graustufendarstellung erkennt man die Vibrationslinie des
Luftsauerstoffs mit den angrenzenden Rotationsflügeln. Die Linien des im ganzen Raum
verteilten Sauerstoffs verschwinden deswegen nach oben und unten, da die Abbildungsoptik nicht vignettierungsfrei2 ist. Aus den Rotationsflügeln kann die Temperatur der
Gasphase (siehe Kap. 2.1.4, S. 28) in Abhängigkeit vom Abstand zur Tropfenkette
bestimmt werden. Etwa in der Bildmitte liegt das Ramansignal des Acetons. Der
schwarze Fleck an der Position der Tropfenkette stammt von der Flüssigphase des
Acetons. Da die Tropfen zum größten Teil aus Aceton bestehen, ist dieses Signal am
intensivsten. Das schmale Band, das in der Bildmitte von links nach rechts verläuft,
stammt vom Untergrund des Aceton-Flüssigphasensignals. Rechts ober- und unterhalb
des Aceton-Flüssigphasensignals sind zwei schwache Linien im Bereich der Gasphase
2
Die Vignettierung ist eine mechanische Einengung eines schräg durch ein optisches System tretenden
Strahlenbündels. Hierdurch tritt eine Minderung der Bestrahlungsstärke am Bildfeldrand ein.
MEßDATENERFASSUNG UND AUSWERTUNG
105
zu erkennen. Sie zeigen an, daß auch das Aceton teilweise verdunstet. Im rechten Teil
der Graustufendarstellung findet sich das Acetylensignal. Das Gasphasensignal des
desorbierten Acetylens besteht aus einer intensiven schwarzen Linie und zwei sehr viel
schwächeren Linien links davon. Zu beiden Seiten dieser Vibrationslinien des Acetylens
lassen sich schwach noch die dazugehörigen Rotationsflügel erkennen. Prinzipiell kann
auch aus diesen die Temperatur bestimmt werden. Das Flüssigphasensignal des noch
gelösten Acetylens ist links neben der intensivsten Vibrationslinie an der Position der
Tropfenkette als dunkler Fleck zu erkennen.
Anhand Bild 4.8 läßt sich eindrucksvoll das Potential der zweidimensionalen RamanSpektroskopie zeigen. Gas- und Flüssigphase können gleichzeitig detektiert, aber
dennoch spektroskopisch getrennt werden. Zusätzlich erhält man eine örtliche
Auflösung entlang des anregenden Laserstrahls. Die Quantifizierung der Signale wird in
Kap. 5.2 (S. 139ff) beschrieben.
4. EXPERIMENTELLER AUFBAU
106
4.5 Weitere experimentelle Aufbauten
In diesem Kapitel werden die experimentellen Aufbauten beschrieben, die wichtig für
den Gesamtaufbau oder für Teilexperimente sind, die aber nicht zum Kern der
experimentellen Anordnung gehören.
4.5.1 Das Versorgungssystem des Schwingblendengenerators
In Kapitel 4.2 wurde die Erzeugung einer Tropfenkette durch einen Schwingblendengenerator (SBG) beschrieben. Um eine monodisperse Tropfenkette mit dem SBG
erzeugen zu können, ist es jedoch äußerst wichtig, daß die Flüssigkeitszufuhr konstant
gehalten wird. Kommerziell erhältliche SBG
[TSI 82]
werden mit Spritzenpumpen
betrieben, welche die unangenehme Eigenschaft besitzen, daß der Spritzenkolben
manchmal klemmt, was Druckschwankungen nach sich zieht. Eine andere Möglichkeit,
der Flüssigkeit einen Druck aufzuprägen, ist die Beaufschlagung eines Gasballastes, der
wiederum konstant zu halten ist. Gasdruckregler scheiden dafür aus, da deren
Regelbereich
wiederum
für
Druckschwankungen
sorgt.
Wird
die
Gasdruckbeaufschlagung mit einem großen Druckspeicher [LIN 90a] verbunden, so werden
mechanisch bedingte Druckschwankungen vermieden. Nach diesem Grundprinzip
funktioniert das von Borchers [BOR 94] entwickelte Fördersystem, dessen Aufbau für diese
Arbeit in weiten Teilen übernommen wird.
Den schematischen Aufbau der gesamten Versorgungseinrichtung zeigt Bild 4.9. Sie
kann grob in 4 Baugruppe unterteilt werden:
• das Versorgungssystem,
• die Gas- und Flüssigkeitszuführung,
• das Gasdosiersystem und
• die Druckluftversorgung.
WEITERE AUFBAUTEN
107
Druckminderer
Volumenstromregler
Gasmischbatterie
Flüssigkeitszuführung
und - filtration
Gasballast
Pressluft
50 L
Belüftung
Flüssigkeitsreservoir
Kugelventil
Gaszuführung
Filter
Druckmesser
Spülung
SBG
Bild 4.9: Schematischer Aufbau der gesamten Versorgungseinrichtung des SBG.
Der zentrale Teil der Versorgungseinrichtung ist das Versorgungssystem mit dem
Flüssigkeitsreservoir (Hoke, Modell 4HD500). In dem Flüssigkeitsreservoir kann die
Flüssigkeit, mit der der SBG betrieben werden soll, mit einem Gas gemischt und dann
mit konstantem Druck aus einem Gasballast (Preßluftflasche, 50 l) beaufschlagt werden.
Das Gewicht des Flüssigkeitsreservoirs wird von einer Präzisionswaage (Sartorius,
Modell LC 3200 D) bestimmt und in wählbaren Zeitabständen von einem PC
aufgenommen (s. Kap. 4.4.1, S. 100), um den Flüssigkeitsmassenstrom durch den SBG
zu bestimmen.
4. EXPERIMENTELLER AUFBAU
108
Die
Aufbereitung
der
Flüssigkeitszuführung.
Über
Flüssigkeitsreservoirs
zum
Flüssigkeit
geschieht
ein
Dreiwegeventil
SBG
unterbrochen
durch
wird
und
die
mit
die
Gas-
und
Verbindung
des
der
und
Gas-
Flüssigkeitszuführung hergestellt. Die zuzuführende Flüssigkeit wird von einem
Flüssigkeitsfilterbehälter (Sartorius, Modell SM 16263/67) mittels Druckluft in den
Vorratsbehälter befördert. Soll ein Gas in die Flüssigkeit eingelöst werden, wird das
vom Gasdosiersystem bereitgestellte Gas durch die Flüssigkeit im Vorratsbehälter
geleitet, bis Sättigung eintritt. Um eine Übersättigung zu vermeiden, wird das Gemisch
einige Stunden stehen gelassen.
Bei den für diese Arbeit benötigten Gemischen werden die Gase bei
Umgebungsdruck (1 bar) eingelöst. Über der Flüssigkeitsoberfläche stellt sich eine
Gasatmosphäre mit einem Partialdruck von 1 bar ein, da die Gasballastzuleitung
entlüftet wird. Für die Inbetriebnahme des SBG wird die Entlüftung geschlossen und der
Druck im Flüssigkeitsreservoir erhöht, indem über die Gaszuführung Stickstoff
hinzugegeben wird, bis sich der Gasballastdruck einstellt. Erst dann wurde der
Gasballast zugeschaltet. Der Druckaufbau durch Stickstoff ist nötig, da auf diese Weise
der Partialdruck des einzulösenden Gases konstant bleibt. Anderenfalls würde eine
Erhöhung des Partialdrucks des einzulösenden Gases zu einer weiteren Einlösung des
Gases in die Flüssigkeit führen, sodaß Übersättigung eintritt. Eine Diffusion des Gases
vom Flüssigkeitsreservoir in Richtung des Gasballastes ist vernachläßigbar, da die
Zuleitung zum Flüssigkeitsreservoir aus einer ca. 10 m langen Edelstahlkapillare
besteht, die einen Innendurchmesser von 2 mm besitzt.
Das Gasdosiersystem besteht aus drei Massendurchflußreglern der Firma MKS (Typ
1259C, mit den Bereichsendwerten 10, 100 und 1000 sccm 1) und zwei Massenflußmessern der Firma Tylan (Typ FM-380, mit den Bereichsendwerten 5 und 25 slm 2), die
parallel angeordnet sind. Über eine Vakuumpumpe (Edwards, Modell BS2212) kann das
Gasdosiersystem evakuiert werden, um aggressive Medien, die auf den Zuleitungs1
standard cubic centimeters per minute = 1 Ncm/min (Norm cm3/min) bezogen auf 1013 mbar, 0°C nach
DIN 1871, 28400, 1343 u.a. [MKS 93] .
2
standard liter per minute. Näheres siehe Fußnote 1
WEITERE AUFBAUTEN
109
innenwänden adsorbiert sein können, zu entfernen und die Massenflußregler / -messer
zu kalibrieren (s. Anhang B, S. 157ff). Das Gasdosiersystem wurde auch eingesetzt, um
Kalibrationsmessungen an einer Edelstahlküvette (Eigenbau) durchzuführen.
Für die Druckluftversorgung wird die zentrale Preßluft gereinigt (Ölabscheider:
SMV, Modell EAF 200; Partikelfilter: Zander, Modelle HSA1DD-1.St. und HSA1DD2.St.) und über zwei Druckminderer (SMC, Modell IR202) den jeweiligen Verbrauchern
zugeführt.
Wird der SBG in Betrieb genommen, so fließt die Flüssigkeit über das
Dreiwegeventil durch ein Partikelfilter (Eigenbau; Membranfilter: Schleicher & Schuell,
Modell RC 50, Porenweite 0.45 µm) zum SBG. Durch Öffnen eines Überlaufventils
kann die Flüssigkeit zu Reinigungszwecken ungehindert aus dem SBG in einen
Auffangbehälter austreten.
Die Teile der Versorgungseinrichtung, die mit der Tropfenkettenflüssigkeit in
Berührung kommen, bestehen aus Edelstahl oder PTFE (Teflon), wie z.B. alle
Zuleitungen (∅a = 3 mm, ∅i = 2 mm). Bei den Ventilen des Gasdosiersystems handelt
es sich um Kippventile (Hoke, Modell 1513G6Y/MM). Für Versorgungssystem und die
Gas- und Flüssigkeitszuführung werden Diaphragmaventile (Hoke, Modell NOVA)
eingesetzt.
Nach Einbau neuer Bauteile, z.B. Zuleitungen, werden diese zu Reinigungszwecken
mit filtrierten Leitungswasser einige Tage gespült.
Bei Untersuchungen an Strukturresonanzen des inelastischen Streulichts
[MOR 95]
(Outputresonanzen, s. Kap. 2.3, S. 46ff) ist zu beobachten, daß sich die spektrale Lage
der Resonanzen mit der Zeit ändert, und zwar sowohl zu längeren als auch zu kürzeren
Wellenlängen. Die Ursache dessen ist eine langsame Änderung der Tropfengröße durch
Temperaturänderungen des Gasballastes. Dazu folgende Abschätzung:
Für den Volumenstrom V& der Flüssigkeit, die durch die Schwingblende tritt gilt die
Kontinuitätsgleichung
V& = v ⋅ A
(4.10)
4. EXPERIMENTELLER AUFBAU
110
mit dem Blendenfläche A und der Flüssigkeitsgeschwindigkeit v, die in guter Näherung
aus der Bernoullischen Gleichung
p i = pa +
1
ρv 2
2
(4.11)
bestimmt werden kann. pi ist der vom Gasballast aufgeprägte Druck der Flüssigkeit vor
der Schwingblende und pa der Umgebungsdruck, den der Flüssigkeitsstrahl annimmt.
Der zweite Term, der die Flüssigkeitsdichte ρ beinhaltet, beschreibt den dynamischen
Druck der Flüssigkeit. Setzt man Gl. 4.11 und Gl. 4.10 in Gl. 4.7 ein und faßt die Drücke
zum Differenzdruck ∆p zusammen, so erhält man den Tropfendurchmesser
dt = const. ⋅
6
∆p
(4.12)
mit der Konstanten
const. =
3
6
πf
2
ρ
.
(4.13)
Unter Annahme konstanten Umgebungsdrucks pa ist die Tropfengröße nur vom Druck
des Gasballastes abhängig. Setzt man die thermische Zustandsgleichung des idealen
Gases
p ⋅V
= konstant
T
(4.14)
voraus, und nimmt an, daß sich das Gasvolumen nicht ändert, so erhält man die
Tropfengröße in Abhängigkeit von der Temperatur. Über das Verhältnis zweier
Temperaturen läßt sich nun das Verhältnis der sich einstellenden Tropfendurchmesser
berechnen:
⎛T ⎞
d t1
x
= 1 = ⎜ 1⎟
dt 2
x2
⎝ T2 ⎠
1
6
.
(4.15)
Ein Mie-Parameter von x1 = πdt1/λ = 300 ändert sich demnach bei einer Temperaturänderung von T1 = 300 K auf T2 = 299 K um 0.17. Die spektrale Lage einer Output-
WEITERE AUFBAUTEN
111
resonanz bei λ = 600 nm würde dabei um 0.33 nm wandern. Für Untersuchungen von
Strukturresonanzen muß daher die Temperatur des Gasballastes konstant gehalten
werden.
Eine Änderung des Gasballastdruckes erfährt man auch durch die Abnahme des
Flüssigkeitsvolumens und der damit einhergehenden Zunahme des Gasballastvolumens.
Die Abschätzung der Tropfengrößenänderung geschieht analog, nur die Temperatur von
Gl. 4.14 wird konstant gehalten. Typischerweise erhält man einen Flüssigkeitsdurchsatz
von 50 ml/h. Das Gasballastvolumen beträgt 50 l, so daß sich Druck und Volumen um
ca. 1% pro Stunde ändern. Ein Mieparameter von x1 = 300 würde sich damit um 0.05 pro
Stunde verringern. Bei typischen Meßzeiten von einigen Minuten oder weniger ist daher
das Gasballastvolumen von 50 l ausreichend groß.
Die Änderung der Tropfengröße kann auch durch die Anregungsfrequenz f (Gl. 4.7,
S. 80) erfolgen. Bei der Frequenzstabilität des eingesetzten Frequenzgenerators (HP,
Model 335B) von 5⋅10-6 würde sich ein Mie-Parameter von x1 = 300 bei der Frequenz
f = 200 kHz nur um 0.0005 ändern. Die Frequenzstabilität des Frequenzgenerators ist
daher als Fehlerursache für sich ändernde Tropfengrößen auszuschließen.
Aus den oben gemachten Abschätzungen sieht man, daß die Temperatur des
Gasballastes die nachhaltigste Fehlerquelle im Versorgungssystem des SBG darstellt,
die zu Schwankungen der Tropfengröße führen kann.
4.5.2 Messung von Tropfengeschwindigkeit und
Tropfenaufenthaltsdauer
Um Zeitaussagen über die Kinetik von Diffusionsprozessen an Partikeln einer
Tropfenkette machen zu können, ist es notwendig, die Aufenthaltsdauer eines Tropfens
in seiner Atmosphäre zu kennen. Da ein vollständiges Modell für die Beschreibung des
Fallprozesses einer Tropfenkette nicht existiert, mußte der Tropfenaufenthaltsdauer
experimentell bestimmt werden. Eine idealisierte Modellrechnung zur Ermittlung des
4. EXPERIMENTELLER AUFBAU
112
Widerstandsbeiwertes von Einzeltropfen in einer Tropfenkette findet man bei Liu et al.
[Liu 88]
. Zur Bestimmung der Aufenthaltsdauer der Tropfen muß die Tropfen-
geschwindigkeit als Funktion des Abstandes vom Tropfengenerator gemessen werden.
Dazu bieten sich verschiedene Methoden an:
Tropfengeschwindigkeit aus Beugungmuster
Wird eine monodisperse Tropfenkette mit einem Laser beleuchtet, so bildet sich ein
Interferenzmuster aus konzentrischen Ringen und horizontalen Streifen (siehe Bild 4.4,
S. 88). Die horizontalen Streifen entsprechen den Beugungsmaxima, die durch die als
Strichgitter fungierende Tropfenkette entstehen. Der Abstand zwischen den Streifen d ist
daher ein Maß für den Abstand zwischen den Tropfen [BEG 93]
l =
λs
λs
≈
,
d cos α
d
(4.16)
wobei λ die Laserwellenlänge und s der Abstand zwischen Tropfenkette und Schirm ist,
auf dem der Abstand zwischen den Streifen gemessen wird. Die Näherung auf der
rechten Seite der Gl. 4.16 gilt für kleine Winkel α, wenn das Verhältnis d/s << 1 ist. Die
Tropfengeschwindigkeit v an einer Position z unterhalb des Generators hängt vom
Tropfenabstand l und von der Anregungsfrequenz f ab, so daß [MOO 95]
v( z ) = f ⋅ l =
f λs
d( z )
.
(4.17)
Diese Methode zur Messung der Tropfengeschwindigkeit eignet sich nur, wenn der
Abstand zwischen den Tropfen konstant ist. Dies ist in der Regel nur bei den ersten
10 mm unterhalb des Generators der Fall
[DEV 98]
. Bei größeren Abständen verwaschen
die horizontalen Streifen zunehmend und deren Abstand untereinander ist nicht mehr
bestimmbar.
WEITERE AUFBAUTEN
113
Doppellichtschrankenmethode
Für die in dieser Arbeit beschriebenen Messungen wird eine sogenannte Doppellichtschrankenmethode zur Geschwindigkeitsmessung eingesetzt: Die beleuchtete
Tropfenkette wird mittels eines Objektivs (Nikon, 50 mm, 1:2) auf eine DoppelPhotodiode (Enatechnik, LD2-5T) abgebildet. Das Bild jedes Tropfens wandert über
beide Photodioden und man erhält zwei zueinander zeitverzögerte Signale, die mit Hilfe
eines PCs ausgewertet werden. Den experimentellen Aufbau hierzu zeigt Bild 4.10.
Die Tropfenkette wird mit einem nichtfokussierten Laserstrahl beleuchtet. Die
Vergrößerung der Abbildung wird mit Hilfe eines geeichten Maßstabes (Melles Griot,
USAF Test Target) zu V = 14.2 ± 0.15 bestimmt. Der Abstand der beiden Dioden sollte
klein gegenüber der Bildweite sein und wird mit einem kalibrierten Meßokular
kontrolliert: a = (553.5 ± 5) µm.
Bild 4.10: Schematische
Darstellung
geschwindigkeitsmessung.
des
Versuchsaufbaus
zur
Tropfen-
4. EXPERIMENTELLER AUFBAU
114
Damit läßt sich aus der Zeitdifferenz ∆t der beiden Photodiodensignale die
Geschwindigkeit
v( z ) =
a
∆t ( z ) ⋅ V
(4.18)
der Tropfen in einem bestimmten Abstand z zum Generator bestimmen. Dafür wurde ein
exponentieller Abfall der Form
z
v( z ) = v ∞ + A ⋅ exp⎛⎜ − ⎞⎟
⎝ B⎠
(4.19)
A = v0 − v∞
(4.20)
mit
angenommen. Hierin bedeuten v∞ die Sedimentationsgeschwindigkeit der Tropfenkette,
v0 die Anfangsgeschwindigkeit und B eine Wegkonstante, die die Abbremsung
beschreibt. Diese Funktion wurde an die gemessenen Geschwindigkeiten angepaßt und
so die Parameter v∞, A und B berechnet.
Durch Integration der Verweildauern über die Wegelemente erhält man nun die
Tropfenaufenthaltsdauern in Abhängigkeit zum Generatorabstand [BRO 81]:
z
t( z ) =
1
∫ v(z) dz
(4.21)
0
=
⎛ v + A exp( − z B ⎞
z
B
+
⋅ ln ⎜ ∞
⎟
v∞
v∞
v∞ + A
⎝
⎠
.
(4.22)
Die Tropfenkette zerfällt, bevor die Sedimentationsgeschwindigkeit v∞ erreicht wird,
und man erhält ein Spray, dessen Abbremsverhalten sich von dem der Tropfenkette
unterscheidet.
WEITERE AUFBAUTEN
115
Tropfenaufenthaltsmessungen
Mit der Doppellichtschrankenmethode werden die Tropfenaufenthaltsdauern für
verschiedene Parameter der Tropfenkette gemessen. Dabei wurden einzelne Parameter
von folgender Grundeinstellung variiert:
• Druckdifferenz:
2.5 bar,
• Tropfenerzeugungsfrequenz: 120 kHz,
• Durchmesser der Blende:
20 µm,
• Tropfenmedium:
H2O.
Bild 4.11 zeigt die Ergebnisse bei Variation der Druckdifferenz.
Bei der Variation des Druckes sieht man, daß sich die Tropfenaufenthaltsdauer bei
gleichem Abstand mit zunehmendem Druck verkürzt. Dieses Verhalten ist annähernd
linear, wie in Bild 4.12 zu sehen. Dort wird das Verhältnis der Graphen von 1.5, 2.5 und
3.5 bar zu dem von 4.5 bar aufgetragen. Außerdem kann aus Bild 4.12 der Faktor für
12
Tropfenaufenthaltsdauer t / ms
1.5 bar
10
8
2.5 bar
6
3.5 bar
4
4.5 bar
2
0
0
10
20
30
40
50
60
70
80
Abstand zum Generator z / mm
Bild 4.11: Tropfenaufenthaltsdauer als Funktion des Ballastdruckes.
90
100
4. EXPERIMENTELLER AUFBAU
116
1.1
Verhältnis zwischen den Kurven aus Abb. 4.11
Lineare Regression
1.0
Verhältnis
0.9
0.8
0.7
0.6
0.5
0.4
0.3
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Ballastdruck / bar
Bild 4.12: Verhältnis der Kurven aus Bild 4.11 als Funktion des Ballastdruckes.
Die durchgezogene Linie ist eine lineare Regression der Meßpunkte.
einen Druck entnommen werden, der nicht gemessen wird, so daß auch für diesen Druck
die Tropfenaufenthaltsdauer bestimmbar wird.
Eine Variation der Erzeugerfrequenz (70, 120, 170, 220 und 270 kHz) führt zu keinen
nennenswerten Unterschieden in der Tropfenaufenthaltsdauer, wie aus Bild 4.13 a zu
entnehmen ist. Damit ändert sich für verschiedene Tropfengrößen einer Tropfenkette
nicht die Tropfengeschwindigkeit und somit auch nicht die Tropfenaufenthaltsdauer.
Aus Bild 4.13 a kann man auch die Reproduzierbarkeit des Meßverfahrens erkennen.
Der Fehler für die Aufenthaltsdauern wird für Grundeinstellungsbedingungen und einem
Generatorabstand von 100 mm mit 3.5 % (3σ) bestimmt.
Verringert man den Durchmesser der Blende, so verkleinert sich nicht nur die
Tropfengröße, sondern auch die Austrittsgeschwindigkeit der Tropfen. Dies hat zur
WEITERE AUFBAUTEN
117
Folge, daß die Aufenthaltsdauern zunehmen (Bild 4.13 b) und die Tropfenkette früher
zerfällt. Dem kann durch Erhöhung des Vordrucks entgegengewirkt werden.
Wechselt man das Tropfenmedium, so verlängern sich die Aufenthaltsdauern mit
abnehmender Dichte des Mediums. In Bild 4.13 c ist dies für Wasser und Ethanol
dargestellt. Für Aceton erhält man etwa die gleichen Aufenthaltsdauern wie für Ethanol,
da beide Medien annähernd dieselbe Dichte besitzen.
4. EXPERIMENTELLER AUFBAU
118
8
Tropfenaufenthaltsdauer t / ms
7
6
5
4
3
2
1
a.)
0
0
10
20
30
40
50
60
70
80
90
100
Abstand zum Generator z / mm
10
Tropfenaufenthaltsdauer t / ms
9
8
5 µm
10 µm
7
15 µm
6
5
4
25 µm
3
2
b.)
1
0
0
10
20
30
40
50
60
70
80
90
100
Abstand zum Generator z / mm
Tropfenaufenthaltsdauer t / ms
8
7
6
Ethanol
5
Wasser
4
3
2
1
c.)
0
0
10
20
30
40
50
60
70
80
90
100
Abstand zum Generator z / mm
Bild 4.13: Tropfenaufenthaltsdauern als Funktion (a) der Generatorfrequenz (70,
120, 170, 220 und 270 kHz), (b) des Blendendurchmessers (5, 10, 20
und 25 µm) und (c) des Tropfenmediums (Wasser und Ethanol).
WEITERE AUFBAUTEN
119
WEITERE AUFBAUTEN
119
4.5.3 Der Tropfenkettenmonitor
Um den momentanen Zustand der Tropfenkette beobachten zu können, wurde ein
sogenannter Tropfenkettenmonitor konstruiert
[KUE 99]
. Dabei handelt es sich um eine
stroboskopische Beleuchtung der Tropfenkette und ein Mikroskop zur Beobachtung.
Bild 4.14 zeigt den schematischen Aufbau. Mit der Anregungsfrequenz des SBG wird
auch eine lichtstarke LED betrieben. Ein Pulsformer verringert das Puls-PausenVerhältnis zu Pulslängen von 200 ns. Dies entspricht in etwa der Anstiegszeit der LED.
Damit erhält man ein stehendes Bild der Tropfenkette. Mit einer durchstimmbaren
Zeitverzögerung kann dieses Bild kontinuierlich verschoben werden, so daß alle Phasen
der Tropfenbewegung beobachtet werden können. Für die Beobachtung wurde das
Mikroskop mit einem Objektiv ausgestattet, das einen extrem langen Arbeitsabstand
besitzt (Nikon, MTJ-67-200; 20×, AA 19.9 mm). Anstelle des Okulars wurde eine
Mikro-CCD-Kamera (LOT Oriel, „Eyepiece“; Art.Nr. 28099) eingesetzt, die das Bild
der Tropfenkette auf einen Monitor projiziert. Mikroskop und LED besitzen eine
Monitor
Freq.generator
Pulsformer
SBG
CCD
Mikroskop
Zeitverzögerung
LED
Bild 4.14: Schematische Darstellung des Tropfenkettenmonitors.
120
4. EXPERIMENTELLER AUFBAU
gemeinsame optische Achse. Weiterhin kann anstelle der CCD-Kamera auch eine
herkömmliche Fotokamera oder ein Okular eingesetzt werden.
Der Tropfenkettenmonitor ist notwendig, um die Stabilität des Betriebs der
Tropfenkette zu prüfen. Insbesondere für die Messungen der Gasphase zwischen den
Tropfen (siehe Kap. 5.2, S. 136ff) müssen die Tropfen nicht nur monodispers sein und
die Tropfenkette darf keine seitlichen Auslenkungen zeigen, sondern auch das zeitliche
Auftreten der Tropfen muß konstant bleiben. Mit anderen Worten, das stehende Bild der
Tropfenkette darf nicht wandern. Dies passiert jedoch schon bei sehr kleinen Störungen,
wie z.B. bei kleinen Gasturbulenzen kurz unterhalb des SBG. Kleine Störungen
verursachen eine Änderung des Ortes, an dem die Tropfen vom Flüssigkeitsstrahl
abreißen. Tritt dies auf, so verschmiert das Bild der Tropfenkette auf dem Monitor.
Messungen der Gasphase zwischen den Tropfen, bei der eine ähnliche gepulste Technik
eingesetzt wird (siehe Kap. 5.2, S. 136ff), brauchen dann gar nicht erst zu beginnen.
Mit dem Tropfenkettenmonitor kann auch das Abreißen der Tropfen vom
Flüssigkeitsstrahl und das Auftreten von Satellitentropfen direkt beobachtet werden.
In einer einfachen Abwandlung kann der Tropfenkettenmonitor auch ohne Pulsformer
und Zeitverzögerung betrieben werden. Dann muß die LED mit einer Sinusspannung
versorgt werden und die Amplitude so gewählt sein, daß die LED gerade eben emittiert.
Nur im Maximum der Sinusschwingung leuchtet die LED dann kurz auf und man erhält
ebenfalls ein scharfes stehendes Bild der Tropfenkette.
WEITERE AUFBAUTEN
Bild 4.15: Lichtschnitt zur Sichtbarmachung der Gasströmung um einen
Schwingblendengenerator (SBG). Von links oben werden der Meßkammer Rauchpartikel zugeführt. Der aufgeweitete Strahl des He-NeLaser kommt von links. Das untere Ende des SBG mit seiner
Piezokeramik (PZT) hat einen Durchmesser von 29 mm. Die Tropfenkette ist deutlich als heller Strich zu erkennen. Deren Tropfen haben
einen Durchmesser von etwa 45 µm und sind am Austritt des SBG
knapp 20 m/s schnell. Man erkennt, wie die Rauchpartikel von der
Gasströmung mitgerissen werden. Detaillierte Aufnahmen vom SBGAustritt zeigen die nächsten Abbildungen. Links oberhalb des PZT ist
ein Wirbel zu erkennen.
121
4. EXPERIMENTELLER AUFBAU
122
4.5.4 Strömungsvisualisierung
Da die Gasphase um die Tropfenkette die Stoff- und Energietransportprozesse an den
Tropfen beeinflußt, wird die Gasströmung kurz unterhalb des Generators wie folgt
qualitativ untersucht: Der Meßkammer werden Rauchpartikel eines Räucherkegels
zugesetzt, die der Gasströmung im wesentlichen folgen. Danach werden die
Tropfenkette und die Rauchpartikel mit einem Laserlichtschnitt beleuchtet. Dazu wird
ein He-Ne-Laserstrahl mit einer Zylinderlinse aufgeweitet. Der Lichtschnitt wird dann
mit einer Videokamera aufgenommen.
Eine Großaufnahme der Meßkammer zeigt Bild 4.15. Die Rauchpartikel werden links
oben der Meßkammer zugeführt. Nähere Einzelheiten sind der Bildunterschrift zu
entnehmen. Bild 4.16 zeigt eine Aufnahme, bei der die Zuströmung der Rauchpartikel
unterbrochen wird, so daß sich die Strömung in der Meßkammer sich selbst überlassen
ist. Die Strömungsverhältnisse kurz unterhalb des Generators zeigen die Aufnahmen von
Bild 4.16: Ähnliche Aufnahme wie die vorherige Abbildung. Jedoch wurde die
Rauchgaszuströmung
unterbrochen
Meßkammer sich selbst überlassen.
und
die
Strömung
in
der
WEITERE AUFBAUTEN
123
Bild 4.17: Strömung in der Nähe des Flüssigkeitsstrahlaustritts. Etwa 2 mm
unterhalb des SBG ist ein Staupunkt zu erkennen. Oberhalb davon
werden die Gaspartikel nach oben zur Austrittsblende hin abgelenkt.
Das rechte Bild ist nicht so stark vergrößert wie das linke. Hier ist der
Einflußbereich der Tropfenkette auf die Rauchgasströmung gut zu
sehen. Beide Aufnahmen werden schräg dargestellt, so daß die
Tropfenkette senkrecht zum Seitenformat angeordnet ist.
Bild 4.17. Beide Aufnahmen haben unterschiedliche Vergrößerungsmaßstäbe. In beiden
Bildern ist ein Bereich zu erkennen, etwa 2 mm unterhalb des SBG, in dem sich die
Strömung verzweigt. Oberhalb davon werden die Gaspartikel nach oben zur
Austrittsblende hin abgelenkt. Während die Verzweigung der Strömung im linken Bild
besser zu erkennen ist, kann im rechten Bild der radiale Einflußbereich der Tropfenkette
auf die Rauchgasströmung besser beobachtet werden.
124
5. MESSUNGEN UND ERGEBNISSE
5 Messungen und Ergebnisse
In diesem Kapitel werden die eigentlichen Ziele dieser Arbeit durch die
Erläuterungen der Vorkapitel fokussiert: Die Messung des Stofftransportes an einer
Kette monodisperser Mikrotropfen. Dazu wird zwischen den Messungen der
Partikelphase (Flüssigkeit) und der Gasphase unterschieden, die in zwei Unterkapiteln
getrennt voneinander erläutert werden. Dies ist notwendig, da für beide Messungen
unterschiedliche Meß- und Auswerteprozeduren angewandt werden.
Für die Untersuchungen des Stofftransportes wird der Desorptionsprozeß von
Acetylengas aus Acetontropfen gewählt. Die Gründe für die Wahl des Systems
Acetylen / Aceton sind in Kapitel 3 (S. 58ff) diskutiert.
5.1 Die Partikelphase
5.1.1 Messung
Zur Herstellung des Flüssigkeitsgemisches wird das Acetylen bei 1 bar in das Aceton
eingelöst. Um eine Übersättigung auszuschließen, wird dieses Gemisch mehrere Stunden
ruhen gelassen. Damit sind 0.96 mol/l Acetylen im Aceton eingelöst. Für die Messungen
wird dieser Lösung ein Druck von 3 bar beaufschlagt. Um den Partialdruck des
Acetylens über der Lösung im Flüssigkeitsreservoir nicht zu erhöhen, wird die Erhöhung
des Drucks durch Zuführung von Stickstoff gemacht, bis der entsprechende Druck
erreicht ist. Danach wird der Gasballast hinzugeschaltet. Dies gewährleistet, daß sich
DIE PARTIKELPHASE
125
während der Messungen die Acetylenkonzentration im Flüssigkeitsreservoir nicht
erhöht.
Der mittlere Durchmesser der Tropfen von 48 µm wird kontinuierlich um etwa 1 %
geändert, indem die Anregungsfrequenz permanent variiert wird. Damit wird über viele
mögliche Resonanzpositionen integriert.
Die Tropfenkette wird durch den Ar+-Laserstrahl mit einer Leistung von 2 W
beleuchtet. Die Fokussierung geschah mit einem 100 mm Achromaten. Der
experimentelle Aufbau ist in Kap. 4 detailliert beschrieben. Der Bildverstärker wird für
diese Messungen nicht eingesetzt.
An verschiedenen Positionen unterhalb des SBG werden in Schritten von je 5 mm
Ramanspektren von den Tropfen aufgenommen. Ein typisches Ramanspektrum der
Acetylen / Aceton-Tropfen zeigt Bild 5.1. Dieses Spektrum wird 20 mm unterhalb des
Generators detektiert, was einer Tropfenaufenthaltsdauer von 1.1 ms entspricht. Die
Intensität / a.u.
Aceton
gelöstes
Acetylen
Luftsauerstoff
0
1500
1600
1700
1800
freigesetztes
gasförmiges
Acetylen
1900
Wellenzahlverschiebung / cm
2000
-1
Bild 5.1: Ramanspektrum der Acetylen / Aceton-Tropfenkette. Dieses Spektrum
wird 20 mm unterhalb des SBG aufgenommen.
5. MESSUNGEN UND ERGEBNISSE
126
Linie des Acetons bei 1712 cm-1 wird als interner Standard zur Bestimmung der
Acetylenkonzentration genutzt. Die Linie des noch in den Tropfen gelösten Acetylens
findet sich bei 1961 cm-1 und die des schon freigesetzten gasförmigen Acetylens ist bei
1977 cm-1 zu erkennen. Bei 1556 cm-1 liegt die Linie des Luftsauerstoffs.
5.1.2 Kalibrierung
Um quantitative Aussagen aus Raman-Signalen erhalten zu können, müssen diese mit
Messungen von definiert hergestellten Gemischen verglichen werden. Diese Gemische
werden in einer temperaturgeregelten Küvette bei einem bestimmten Druck (i.a. für
diese Arbeit bei T = 25°C und Atmosphärendruck) vermessen. Zusätzlich wird das
Gemisch gerührt, um Übersättigungen ausschließen zu können. Die hier untersuchten
Gemische bestehen aus einem Gas, das in einer bestimmten Konzentration in die
Flüssigkeit eingelöst wird. Dazu wird das einzulösende Gas mit einem inerten Gas (i.a.
N2, aber auch Edelgase sind möglich) gemischt und der Flüssigkeit zugeführt.
Die Mischung der Gase erfolgt mit einer Volumenstrommischbatterie, bestehend aus
drei Volumenstromreglern (MKS, Typ 1259C mit den oberen Bereichsendwerten 10,
100 und 1000 st.cm3/min)1. Die Volumenströme durch die einzelnen Regler müssen
kontrolliert bzw. kalibriert werden. Genaue Beschreibungen dazu befinden sich im
Anhang B (S. 157ff).
Der Gesamtdruck pges des Gasgemisches beträgt 1 bar und setzt sich aus den
Partialdrücken pi der einzelnen Komponenten zusammen:
pges =
∑ pi
.
(5.1)
i
Der Partialdruck der jeweiligen Komponente verhält sich zum Gesamtdruck wie das
Verhältnis der einzelnen Volumenströme V& zum Gesamtvolumenstrom V&
i
1
ges
st.cm3/min oder sccm bezieht sich auf den Normzustand eines trockenen Gases bei 0°C und 1013 mbar
nach DIN 1871, 28400, 1343 u.a..
DIE PARTIKELPHASE
p i = p ges
127
V&i
V&ges
.
(5.2)
Die molare Konzentration ci des gelösten Gases bei Erreichen des Gleichgewichtszustandes wird durch das Henry-Dalton-Gesetz beschrieben (s. Kap. 3, S. 68ff).
Zur Ermittlung der Zeit, bis zu der sich ein Konzentrationsgleichgewicht in der
Küvette eingestellt hat, werden Messungen des Gemisches in Abhängigkeit von der Zeit
durchgeführt. Die so ermittelte Einlösezeit wird für die Erstellung der verschiedenen
Gleichgewichtskonzentrationen zugrundegelegt.
Außer den Kalibrationsmessungen kann an der Küvette der Zusammenhang zwischen
der Linienintensität und der Konzentration einer chemischen Komponente ermittelt
werden. Beeinflussen sich die Moleküle verschiedener chemischer Spezies, so kann sich
das im Ramanspektrum widerspiegeln. Dabei kann es zu Veränderungen von Intensität,
spektraler Lage und Form einer Linie kommen. Ansonsten ist mit einem nichtlinearen
Verhältnis zwischen Linienintensität und Konzentration zu rechnen und das
entsprechend zu berücksichtigen. Ist dies nicht der Fall, kann aus einem
Linienintensitätsverhältnis direkt auf die Konzentration einer chemischen Komponente
geschlossen werden.
Zur Prüfung des lineareren Zusammenhangs zwischen der Linienintensität und der
Konzentration für das in dieser Arbeit untersuchte System Aceton - Acetylen sind
Acetylen bei verschiedenen Partialdrücken in Aceton gelöst und die Ramanintensitäten
gemessen worden. Das Verhältnis der Ramanintensitäten von Acetylen zu Aceton wird
gegen die relative Acetylen-Konzentration aufgetragen (Bild 5.2). Es kann ein linearer
Zusammenhang zwischen der Acetylen-Linienintensität und der Konzentration
festgestellt werden.
5. MESSUNGEN UND ERGEBNISSE
128
Verhältnis Acetylen / Aceton
0.30
Messung A
Messung B
0.25
0.20
lin. Regression
0.15
0.10
0.05
0.00
0
10
20
30
40
50
60
70
80
90
100
Acetylen-Konzentration / %
Bild 5.2: Auf das Aceton-Signal normiertes Acetylen-Signal in Abhängigkeit zur
Acetylen-Konzentration im Aceton. Die Acetylen-Konzentration bezieht
sich auf die Sättigungskonzentration. Zusätzlich ist die lineare
Regressionskurve eingezeichnet.
5.1.3 Linienintensität
Die Bestimmung der Konzentration einer chemischen Komponente erhält man durch
Bildung des Linienverhältnisses der Komponenten. Ist die Konzentration einer
Komponente eines binären Stoffgemisches nur marginal vertreten, so kann die
Linienintensität der Hauptkomponente als interner Standard herangezogen werden. Dies
ist meist bei in Flüssigkeit gelösten Gasen der Fall und die Linienintensität der schwach
vertretenen Komponente, bezogen auf die Linienintensität der Hauptkomponente, direkt
ein Maß für deren Konzentration. Ein Vergleich mit Küvettenmessungen bekannter
Zusammensetzung ergibt den absoluten Wert der Konzentration.
DIE PARTIKELPHASE
129
Als Intensität einer Linie kann für eine abschätzende Untersuchung das Maximum
der Linie herangezogen werden. Da das Maximum nur aus einem Punkt besteht, ist diese
Art der Auswertung nicht sehr genau. Einen kleineren Fehler erhält man, wenn das
Integral einer Linie herangezogen wird (Jeder Punkt ist ein Meßpunkt, die Summe ergibt
einen kleineren (relativen) Fehler, Poissonstatistik). In jedem Fall muß natürlich die Art
der Auswertung für Küvettenmessung und Untersuchungsobjekt identisch sein. Dies gilt
selbstverständlich auch für die Berücksichtigung des spektralen Untergrundes.
Wie in Bild 5.1 zu sehen ist, sind die Linien der beiden Acetylenphasen spektral
soweit voneinander getrennt, daß man sie gut getrennt voneinander erkennen kann.
Dennoch beeinflussen sich die Linien gegenseitig. Um die Raman-Intensität des
Flüssigphasensignals (Ifl) und des Gasphasensignals (Ig) zu bekommen, wird diese
Beeinflussung quantifiziert. Dazu werden die relativen Signale beider Phasen
(a = 0.975, b = 0.025, c = 0.161 und d = 0.839; wobei a+b = c+d = 1 ist) um eine
spektrale Lage (1960 cm-1) bestimmt, wie aus Bild 5.3 zu entnehmen ist.
Damit kann aus der Bestimmung der Flächen A1 und A2 aus einem Spektrum mit
beiden Phasensignalen die Intensität beider Phasensignale durch den folgenden Satz von
Gleichungen bestimmt werden:
⎛ A1 ⎞
⎛ a c ⎞ ⎛ I fl = A ⎞
⎟
⎜ ⎟ = ⎜
⎟ ⎜
⎝ A2 ⎠
⎝b d⎠ ⎝ I g ⎠
.
(5.3)
Daraus ergeben sich die Intensitäten beider Phasensignale
I fl = A =
d
c
⋅ A1 −
⋅ A2 = 10304
.
⋅ A1 − 01976
.
⋅ A2
ad − cb
ad − cb
(5.4)
a
b
⋅ A2 −
⋅ A1 = 11976
.
⋅ A2 − 0.0304 ⋅ A1 .
ad − cb
ad − cb
(5.5)
und
Ig =
5. MESSUNGEN UND ERGEBNISSE
130
Intensität / a.u.
A1
A2
C2H2 (g)
C2H2 (fl)
a
d
c
b
0
1900
1920
1940
1960
1980
2000
-1
Raman shift / cm
Bild 5.3: Zwei Ramanspektren von Acetylen in der flüssigen und gasförmigen
Phase. In einem Spektrum, das beide Phasen enthält (z.B. Bild 5.1),
werden die Flächen A1 und A2 bestimmt. Jede Fläche enthält RamanSignale beider Phasen. In Bezug auf die Gesamtfläche einer Phase sind
die relativen Flächenanteile der Flüssigphase a=0.975 und b=0.025,
während die der Gasphase c=0.161 und d=0.839 sind. Aus diesen Daten
können mit Gl. 5.3 die Linienintensitäten beider Acetylenphasen
bestimmt werden.
Der Suffix fl=A in Gl. 5.3 macht deutlich, daß die Intensität des Flüssigphasensignals Ifl
gleich der Intensität IA in Gl. 2.64 (S. 31)
cA = cB ⋅
IA
IB
⎛I ⎞
⎛c ⎞
⋅⎜ B ⎟ ⋅⎜ A ⎟
⎝ I A ⎠ kal ⎝ cB ⎠ kal
ist, mit der die Konzentration cA des noch gelösten Acetylens bestimmt werden kann.
Der Suffix B in dieser Gleichung steht hier für das Aceton.
DIE PARTIKELPHASE
131
5.1.4 Auswertung
Die bisherige Bestimmung der Linienintensitäten für verschiedene Positionen (oder
Tropfenaufenthaltsdauern, siehe dazu Kap. 4.5.2, S. 111ff) unterhalb des SBG hat den
radialen Konzentrationsgradienten des Acetylens in den Tropfen nicht berücksichtigt.
Diese Berücksichtigung wird in Kap. 2.3 (S. 50ff) diskutiert. Demnach wird bei der oben
gemachten Verhältnisbildung der Linienintensitäten (Gl. 2.64) nur scheinbare Konzentrationen bestimmt. Die tatsächliche Konzentration erhält man durch eine nichtlineare
Anpassung der Funktion
c∗A (t , x, c0 , DAB ) =
1
Vt
∫ w(r , x)
c A (r , t , c0 , DAB ) r 2 drdΩ
(5.6)
an die Meßwerte entsprechend Gl. 2.64 (s. Kap. 2.3). Dabei wird von einem
diffusionskontrollierten Konzentrationsprofil cA(r, t, c0, DAB) ausgegangen und Gl. 3.5
angewandt. Da der Diffusionskoeffizient DAB von Acetylen in Aceton nicht bekannt ist,
wird er ebenfalls angepaßt. Auch die Anfangskonzentration c0 muß angepaßt werden, da
der Beginn des Desorptionsprozesses nicht an Tropfen, sondern an dem Flüssigkeitsstrahl, der später in Tropfen zerfällt (Kap. 4.2, S. 79ff), startet. Die kurze
Zeitspanne von 0.2 ms, bis der Desorptionsprozeß an den Tropfen beginnt, wird
ebenfalls berücksichtigt.
5.1.5 Ergebnisse
Für die Gewichtungsfaktoren x (s. Kap. 2.3, S. 50ff) von 0 bis 10 wird in Schritten
von 0.1 die oben beschriebene Anpassung durchgeführt. Man erhält so für jeden
Gewichtungsfaktor einen theoretischen Konzentrationsabfall mit den am besten
angepaßten Werten für c0 und DAB. Es wird ebenfalls die Fehlerquadratsumme des
besten Fits für jeden Gewichtungsfaktor bestimmt. Bild 5.4 zeigt die Diagramme für die
Fehlerquadratsumme, den Diffusionskoeffizienten DAB und die Anfangskonzentration c0
als Funktion des Gewichtungsfaktors x. Im Minimum der Fehlerquadratsumme erhält
man die besten Werte für die angefitteten Parameter: x = 1.7, DAB = 7.1 ⋅ 10-9 m2/s und
c0 = 1.08 mol/l.
5. MESSUNGEN UND ERGEBNISSE
132
Fehler
0.04
a.)
0.03
c0 / mol/l
-9
2
DAB / 10 m /s
0.02
9
8
7
6
5
b.)
1.1
c.)
1.0
0.9
0.8
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
Gewichtungsfaktor x
Bild 5.4: Einfluß des Gewichtungsfaktors x auf die Anpassung der berechneten
Konzentrationsverläufe an die Meßwerte. Für jeden Gewichtungsfaktor
gibt es einen besten Wert für den Diffusionskoeffizienten DAB (b) und die
Anfangskonzentration c0 (c). Die Fehlerquadratsumme für jeden dieser
Wertepaare ist in (a) aufgetragen. Bei x = 1.7 ist der Fehler zwischen
Rechnung und Messung minimal und der beste Fit liefert den Diffusionskoeffizienten DAB = 7.1 ⋅ 10-9 m2/s
und
die
Anfangskonzentration
c0 = 1.08 mol/l.
Die so erhaltene Anfangskonzentration liegt höher als die eigentlich Eingelöste. Der
Grund liegt in den ersten 0.2 ms, in denen noch ein Flüssigkeitsstrahl existiert. Hier
verläuft der Desorptionsprozeß langsamer, weil die Oberfläche kleiner ist. Da die
Berechnung jedoch für Kugeloberflächen durchgeführt wird, scheint die Anfangskonzentration zu hoch. Nach 0.2 ms ist die Anfangskonzentration des Desorptions-
DIE PARTIKELPHASE
133
prozesses der Kugeln 0.81 mol/l. Bis zum Zerfall des Flüssigkeitsstrahls in Tropfen sind
demnach bereits 0.15 mol/l desorbiert.
Für den Diffusionskoeffizienten wurden keine Werte in der Literatur gefunden, so
daß ein Vergleich nicht möglich war. Jedoch findet man in dem Werk von Reid et al.
[REI 86]
einige Abschätzungmethoden, die das gewonnene Ergebnis bestätigen:
Wilke-Chang Abschätzung [WIL 55]
6.5 ⋅ 10-9 m2/s
Nakanishi Korrelation [NAK 78]
7.7 ⋅ 10-9 m2/s
Tyn und Calus Methode [TYN 75]
6.4 ⋅ 10-9 m2/s
Hayduk und Minhas Korrelation [HAY 82]
5.8 ⋅ 10-9 m2/s
Das interessanteste Ergebnis ist, daß die beste Anpassung den Gewichtungsfaktor x = 1.7 liefert. Dies bedeutet, daß die Intensität der Raman-Streuung an
Mikrotropfen auch vom Konzentrationsprofil abhängt. Das meiste Raman-Streulicht
kommt aus der Schale, wo sich weniger Acetylenmoleküle aufhalten als im Kern. Die
tatsächliche mittlere Acetylenkonzentration muß also höher liegen als die Konzentration,
die man nur durch den Linienvergleich erhält. Will man den tatsächlichen zeitlichen
Verlauf der mittleren Acetylenkonzentration bekommen, so muß man mit den
Ergebnissen der Anpassung für die Anfangskonzentration und den Diffusionskoeffizienten und dem Gewichtungsfaktor x = 1 den tatsächlichen Konzentrationsverlauf
berechnen (s.S. 54). Bild 5.5 zeigt die Ergebnisse: Zwei experimentelle Versuchsreihen
sind durch die kreisförmigen und quadratischen Meßpunkte dargestellt. Diese
Meßpunkte ergeben sich aus den Linienverhältnissen, gemäß Gl. 2.64, und entsprechen
den ermittelten scheinbaren Konzentrationen. Die beste Anpassung an diese Meßpunkte
ist durch die gestrichelte Linie gekennzeichnet. Dies entspricht dem scheinbaren
Konzentrationsverlauf
c ∗A (t , x = 17
. , c0 = 108
. mol / l , D AB = 7.1 ⋅ 10 −9 m 2 / s) ,
5. MESSUNGEN UND ERGEBNISSE
134
bei dem eine Gewichtung der Raman-Streuung mit x = 1.7 berücksichtigt wurde. In dem
Modell zur Ermittlung des scheinbaren Konzentrationsverlaufs steckt nicht nur die
Gewichtung, sondern auch der tatsächliche Konzentrationsverlauf
c A (t ) = c ∗A (t , x = 1, c0 = 108
. mol / l , D AB = 7.1 ⋅ 10 −9 m 2 / s) ,
da die Anfangskonzentration c0 und der Diffusionskoeffizient DAB schon für c ∗A
bestimmt
wurden.
Der
tatsächliche
zwei Meßreihen
Anpassung an die Meßwerte unter Berücksichtigung
einer ungleichmäßigen Ausleuchtung der Tropfen
errechnete tatsächliche mittlere Konzentration
0,8
Acetylenkonzentration / mol/l
Konzentrationsverlauf cA(t) ist durch die
0,6
c(t)
0,4
*
c (t)
0,2
0,0
0
2
4
6
8
10
Tropfenaufenthaltsdauer / ms
Bild 5.5: Acetylenkonzentration in Acetontropfen als Funktion der Tropfenaufenthaltsdauer. Die Rechnung mit dem Gewichtungfaktor x = 1.7
simuliert, was bei einem Konzentrationsgradienten beobachtbar ist. Sie
stimmt gut mit den Messungen überein. Die Rechnung mit dem
Gewichtungsfaktor x = 1 gibt den Verlauf der tatsächlichen mittleren
Konzentration wieder.
12
DIE PARTIKELPHASE
durchgezogene
Berücksichtigung
135
Linie
dargestellt.
des
Ihn
ermittelten
c ∗A (t ) ,
indem
unter
Diffusionskoeffizientens
und
der
erhält
man
aus
Anfangskonzentration der Gewichtungsfaktor x = 1 eingesetzt wird (siehe dazu auch
Kap. 2.3, S. 50ff). Für diesen Fall würden alle Bereiche der Tropfen gleich viel zum
Raman-Streulicht beitragen.
Diese Auswertung der Meßdaten zeigt, daß die Gewichtung der Raman-Streuung für
diese Messung ungleichmäßig für Kern und Schale der Mikropartikel verteilt ist. Das
Raman-Signal der Moleküle, die sich in der Nähe der Partikeloberfläche aufhalten, wird
relativ zu denen, die sich im Kernbereich aufhalten, verstärkt. Das kann zwei Gründe
haben: Erstens können Eingangs- und Ausgangsresonanzen angeregt werden, deren
Modenvolumina in der Nähe der Partikeloberfläche lokalisiert sind (s. Kap. 2.2 und 2.3,
sowie Bild 2.3, S. 41). Zweitens ist der Laserfokus in diesen Experimenten nur wenig
größer als der Durchmesser der Partikel. Durch die Bewegung der Partikel durch den
Laserstrahl können so Oberflächenwellen stärker angeregt werden, wenn der Laser die
Tropfen nicht genau in der Mitte trifft [KHA 93] (siehe dazu auch Bild 2.6, S 52).
5. MESSUNGEN UND ERGEBNISSE
136
5.2 Die Gasphase
Ziel der Messung ist es, die Gasphase in nächster Nähe der verdunstenden
Mikropartikel zu bestimmen. Die Kenntnis der Zusammensetzung der Gasphase in
unmittelbarer Nähe der Phasengrenze ist wichtig zur Beschreibung der Absorption und
Desorption von Gasen in bzw. aus mikrometergroßen Tropfen. Bisherige Arbeiten
[VEH 95a+b]
haben gezeigt, daß das Gasprofil in der Nähe von Mikrotropfen zwar mit einer
räumlichen Auflösung von etwa 50 µm gemessen werden konnte, jedoch nur bis zu
einem minimalen Abstand von 100 µm. Der Grund dafür ist ein zufälliges Ändern der
Tropfenkettenposition im Untersuchungsvolumen während der Beobachtungszeit.
Dieses Problem konnte nicht gelöst werden. Um diese Begrenzung der räumlichen
Auflösung zu umgehen, wird eine neue Technik entwickelt: Die gepulste
zweidimensionale Ramanspektroskopie. Dabei handelt es sich um eine stroboskopische
Meßtechnik, mit der die momentane lokale Gaskonzentration zwischen den Tropfen
gemessen werden kann. Messungen und Ergebnisse dieser Technik werden im
Folgenden beschrieben.
5.2.1 Messung
Eine detaillierte Beschreibung des Meßaufbaus wurde in Kap. 4 geliefert. Bild 4.1
(S. 77) zeigt eine Übersichtsskizze des gesamten Aufbaus. Eine genauere Skizze, die den
stroboskopischen Betrieb des Versuchsaufbaus verdeutlicht, zeigt Bild 5.6. Die Einzelkomponenten des optischen Aufbaus sind in Kap. 4.3 beschrieben. Zur stroboskopischen
Detektion wird zwischen dem Monochromator und der CCD-Kamera der Bildverstärker
eingebaut. Der Bildverstärker kann in vorher bestimmten Zeitintervallen auf
Transmission geschaltet werden. Wird der Bildverstärker mit der Anregungsfrequenz
der Tropfenerzeugung getriggert, so werden ganz bestimmte Bereiche der Tropfenkette
selektiv gemessen. Die instationäre Tropfenverdampfung wird auf diese Weise in einen
quasistationären Prozeß transformiert; man erhält ein virtuell eingefrorenes, stehendes
Bild der Tropfenkette. Durch eine einstellbare Verzögerung kann die relative Lage des
DIE GASPHASE
137
Bild 5.6: Skizze des Versuchsaufbaus zur stroboskopischen Detektion.
Streuvolumens zum Tropfen genau eingestellt werden. Auf diese Weise kann die
Gaskonzentration
zwischen
den
Tropfen
auch
in
Tropfenbewegungsrichtung
ortsaufgelöst gemessen werden. Eine Bestimmung der Gasphasenkonzentration in
unmittelbarer Nähe der Tropfenkette ist damit möglich, auch wenn die Tropfenkette
örtlich instabil ist.
Das Gemisch, das dem SBG zugeführt wird, besteht aus Aceton, in das 0.7 mol/l
Acetylen eingelöst wird. Diese Konzentration ist etwas geringer als die Sättigungskonzentration bei 1 bar und 25°C (0.96 mol/l). Erreicht wird dies, indem beim Einlösen
des Acetylens das Gas mit einer definierten Menge Stickstoff verdünnt wird. Damit wird
der Partialdruck (Gesamtdruck: 1 bar) des Acetylens herabgesetzt. Einzelheiten dazu
wurden bereits in Kap. 5.1 beschrieben.
Der Grund für die Herabsetzung der Anfangskonzentration ist ein stabilerer Betrieb
der Tropfenkette. Es zeigt sich, daß bei höherer Anfangskonzentration kein stehendes
5. MESSUNGEN UND ERGEBNISSE
138
Bild der Tropfenkette bei stroboskopischer Beleuchtung möglich ist. Als Grund wird
vermutet, daß der Abreißprozeß der Tropfen vom Flüssigkeitsstrahl durch einen heftigen
Desorptionsvorgang gestört wird. Kurz vor dem Abreißen der Tropfen vom Strahl
existiert ein sehr dünner Flüssigkeitsfaden, von dem sich die Tropfen lösen [EGG 97]. Auch
aus diesem Flüssigkeitsfaden, der im Durchmesser um Größenordnungen kleiner ist als
die Tropfen, desorbiert das eingelöste Acetylen. Dieser Desorptionsprozeß verläuft
wesentlich schneller als beim Tropfen, bedingt durch den kleinen Durchmesser der
Flüssigkeitsfäden (siehe dazu Gl. 3.6, S. 61). Jener heftige Ausgasungsprozeß kann bei
zu hoher Acetylenkonzentration den Abreißprozeß der Tropfen beeinflussen. Die Folge
kann ein sich ändernder Abreißort der Tropfen sein. Das führt zu einem verschmierten,
stehenden Bild der Tropfenkette.
Zur Kontrolle des einwandfreien Zustandes der Tropfenkette wird ein Tropfenkettenmonitor eingesetzt (Kap. 4.5.3, S. 119f). Ein um 90° gedrehtes Bild der Tropfenkette an
der Position, an der sie auch spektral untersucht wird, zeigt Bild 5.7.
Es werden zwei Versuchsreihen zur Messung der Gasphasen unternommen. In der
ersten Versuchsreihe wird das Raman-Signal über die gesamte Länge des Laserstrahles
(oder Eintrittsspaltes des Monochromators) integriert. Damit gehen die örtlichen
Informationen senkrecht zur Tropfenkette zugunsten eines höheren Raman-Signals
verloren. Folgende Daten werden für diese Versuchsreihe eingestellt: Laserleistung 5 W,
Laserfokus ≈ 30 µm,
Abstand
zwischen
Anregungsfrequenz
den
43.9 kHz,
Tropfen ≈ 362 µm,
Tropfendurchmesser
62 µm,
Tropfengeschwindigkeit ≈ 10 m/s,
Monochromatorspalt 600 µm, Zeitfenster 500 ns, Gesamtbelichtungszeit 10 s, Position
Bild 5.7: Stroboskopische Aufnahme der Tropfenkette an der Position, an der sie
spektral untersucht wurde.
DIE GASPHASE
139
5 mm unterhalb des SBG.
Die Zeitverzögerungen werden so gewählt, daß Messungen mit einer axialen
Ortsverschiebung von 24 µm erreicht werden. Durch den Laserfokusdurchmesser von
≈ 30 µm und die Geschwindigkeit der Tropfen erhält man eine axiale Ortsauflösung von
≈ 40 µm. Die so erhaltene Sequenz von Spektren ist in Bild 5.8 dargestellt. Man erkennt,
daß bei einer axialen Position zwischen 100 und 350 µm das Flüssigphasensignal des
Acetylens (Acetylen(fl): 1961 cm-1, Untergrund: Aceton) fast vollständig verschwunden
ist. Daher ist bei diesen Positionen das Gasphasensignal des Acetylens besser zu
erkennen. Die Stickstofflinie der Luft dient als Referenzlinie, so daß aus den Spektren
direkt die Konzentrationsverteilung des Acetylengases zwischen den Tropfen bestimmt
werden kann.
Um auch die Konzentrationsverteilung des Acetylengases senkrecht zur Tropfenkette
bestimmen zu können, wird in einer zweiten Versuchsreihe die CCD-Kamera insgesamt
ausgelesen. Die Beschreibung der zweidimensionalen Spektroskopie wurde in
Kap. 4.4.2 (S. 101ff) gemacht.
Abweichend zu der ersten Versuchsreihe werden das Zeitfenster nun auf 1 µs und die
Gesamtbelichtungszeit auf 120 s verlängert. Die sonstigen Bedingungen bleiben
erhalten. Bild 5.9 zeigt eine Graustufendarstellung der Intensitätsverteilung auf dem
CCD-Chip für eine axiale Position zwischen den Tropfen.
5.2.2 Auswertung
Zur Auswertung der zweidimensionalen Darstellung wird das Bild in seine
horizontalen Linien aufgespalten. Jede Linie entspricht einem Spektrum in einem
bestimmten Abstand senkrecht zur Tropfenkette mit einer örtlichen Ausdehnung von
5.3 µm. Die örtliche Auflösung senkrecht zur Tropfenkette beträgt ≈ 37 µm.
5. MESSUNGEN UND ERGEBNISSE
140
a.u.
Intensität /
15
10
5
2400
We
ll
ver
sch enza
hl
ieb
ung / c m 1
2300
2200
0
2100
100
200
300
axial
e Pos
400
ition
/ µm
2000
500
Bild 5.8: Raman-Spektren von der Aceton / Acetylen - Tropfenkette an
verschiedenen axialen Positionen. Spektren mit einer hohen
Signalstärke zeigen die Anwesenheit eines Tropfens im
Meßvolumen. Zwischen den Tropfen ist nur das Acetylensignal in
der Gasphase (bei 1973 cm-1) sichtbar. Bei 2331 cm-1 liegt die
Linie des Luftstickstoffs.
Jedem dieser Spektren werden nun die Reinstoffspektren der Einzelkomponenten
(Acetylen(g), Acetylen(fl), Aceton, Stickstoff) und eine Gerade angepaßt. Damit erhält
man relative Konzentrationen für jede Spezies in Abhängigkeit vom Abstand der
Tropfenkette. Durch Normierung des Acetylengassignals auf das Stickstoffsignal erhält
man die absolute Acetylenkonzentration in der Gasphase. Dabei wird berücksichtigt, daß
der relative Stickstoffanteil der Luft 79 % beträgt. Dies wird für 23 axiale Positionen in
äquidistanten Abständen von ≈ 20 µm wiederholt, und zwar nicht direkt nacheinander in
DIE GASPHASE
141
Schritten von 1 µs, sondern in 4 µs-Schritten (Zeitverzögerungssequenz in µs: 1, 5, 9, ...,
2, 6, ..., 3, 7, ...). Das geschieht aus zwei Gründen: Erstens konnte die Tropfenkette
jederzeit den Betrieb einstellen, sodaß man bei einem Ausfall der Tropfenkette einige
äquidistante Daten gemessen haben kann. Zweitens erhält man bei dieser
Meßreihenfolge Informationen über die Reproduzierbarkeit der Meßmethode.
C2H2(lq)
C2H2(g)
2000
Acetonuntergrund
2100
2200
2300
Wellenzahlverschiebung / cm
N2
-1
Bild 5.9: Logarithmische, invertierte Graustufendarstellung der Intensitätsverteilung auf dem CCD-Detektor. Horizontal erhält man eine spektrale
Auflösung - wie durch das Spektrum angedeutet - und vertikal die
räumliche Auflösung senkrecht zur Tropfenkette (bzw. entlang des
Laserstrahls).
142
5. MESSUNGEN UND ERGEBNISSE
5.2.3 Ergebnisse
Fügt man die gemessenen Konzentrationsdaten in einem Kontourplot zusammen, so
erhält man eine zweidimensionale Konzentrationsverteilung des freigesetzten,
gasförmigen Acetylens. Dies ist in Bild 5.10 in einer Graustufenskalierung dargestellt.
Da senkrecht zur Tropfenkette Rotationssymmetrie vorliegt, ist die Gasverteilung im
Raum bestimmt. Die Flugrichtung der Tropfen ist von oben nach unten. Im oberen
Bereich des Bildes ist ein Tropfen durch ein Oval1 angedeutet. Um die Tropfen befindet
sich ein weißer Bereich, der durch die Einflußsphäre der Tropfen verursacht wird. Hier
kann kein gasförmiges Acetylen detektiert werden.
Hinter den vorausfliegenden Tropfen (unten) erkennt man einen „Schweif“ erhöhter
Acetylenkonzentration. Die Einstrahlung des anregenden Lasers erfolgt von links nach
rechts. Die scheinbaren höheren Acetylenkonzentrationen rechts von den Tropfenpositionen stammen von der Deformation des Laserstrahls durch die Tropfen.
Erwartungsgemäß nimmt die Konzentration des desorbierten Acetylens mit
zunehmendem Abstand zur Tropfenkettenachse ab. Die höchste Acetylenkonzentration
ist ungefähr ein Promille. Sie wird hinter den Tropfen, relativ zur Tropfenausbreitungsrichtung, und nahe der Tropfen gemessen. In der Nähe des Tropfeneinflußbereichs
scheint die Acetylenkonzentration abzunehmen. Dies ist ein Artefakt und auf die
Fitprozedur sowie die Kontourplotberechnung zurückzuführen.
Die lineare zweidimensionale gepulste Raman-Spektroskopie liefert neben der
Gaszusammensetzung auch Informationen über die Flüssigphase. Das kann bei dem
oben beschriebenen Auswerteverfahren zur Kontrolle genutzt werden, da die
Flüssigphasensignale nur an der Position der Tropfen auftreten dürfen. Tatsächlich sind
diese Ramansignale des noch gelösten Acetylens und des Acetons nur an der
Tropfenposition meßbar, wie Bild 5.11 zeigt.
1
Das Oval kommt durch die Skalierung der Achsen in Bild 5.10 zustande.
DIE GASPHASE
143
C2H2 (g)Konz. / ‰
500
axiale Position / µm
0.967
400
300
200
< 0.14
100
-600
-400
-200
0
200
400
600
Abstand von der Tropfenkette / µm
Bild 5.10: Zweidimensionale Graustufendarstellung der Konzentrations-
verteilung des freigesetzten, gasförmigen Acetylens zwischen den
Tropfen einer Aceton/Acetylen - Tropfenkette. Die Tropfen
bewegen sich in dieser Darstellung von oben nach unten. Die
Einstrahlung durch den Laser geschieht von links nach rechts.
Bei der axialen Position 160 µm ist der „Schweif“ erhöhter
Acetylenkonzentration des voraus fliegenden Tropfens gut zu
erkennen.
5. MESSUNGEN UND ERGEBNISSE
600
400
200
100
0
-200
-400
200
300
axial
e Pos
ition 400
/ µm
A
Tr bst
op an
fen d v
ke on
tte de
/µ r
m
0
500
-600
n / a.u.
Acetonkonzentratio
tion / a.u.
Acetylenkonzentra
144
600
400
200
100
200
300
axial
e Pos
ition 400
/ µm
500
A
Tr bst
op an
fen d v
ke on
tte de
/µ r
m
0
0
-200
-400
-600
Bild 5.11: Die Konzentrationen der Partikelphase in willkürlichen Einheiten (a.u.
arbitrary units) als Funktion des Abstandes zur Tropfenkette und in
Richtung der Tropfenfortbewegung: das noch gelöste Acetylen (links
oben) und das Aceton (rechts unten) der Tropfen.
5.2.4 Fazit
Die Messung der Partikelphase des Desorptionsprozesses von Acetylen aus
Acetontropfen ergibt die Ermittlung des Diffusionskoeffizienten von Acetylen in Aceton
zu DAB = 7.1 ⋅ 10-9 m2/s und eine Bestimmung der Gewichtung der Raman-Streuung aus
den Mikropartikeln. Dabei wird festgestellt, daß bei diesen Messungen mehr RamanSignal aus den oberflächennahen Bereichen kommt, als aus dem Kern der Partikel.
DIE GASPHASE
145
Die Nachweisgrenze der Flüssigphase des Acetylens beträgt 1 mmol/l. Dies
entspricht den Nachweisgrenzen wässriger Lösungen
[VEH 95a]
. Eine Zeitauflösung von
1 µs über einen Zeitraum von bis zu 20 ms wurde erreicht.
Mit der Raman-Spektroskopie können Gas- und Flüssigphase getrennt voneinander
beobachtet werden.
Die Messung der momentanen lokalen Gaskonzentration zwischen den Tropfen der
Tropfenkette ergibt eine maximale Acetylenkonzentration von 1 Promille in
unmittelbarer Nähe der Tropfen. Die Nachweisgrenze in der Gasphase beträgt etwa
100 µmol/mol für das hier untersuchte System. Die räumliche Auflösung beträgt jeweils
ungefähr 40 µm in Richtung der Tropfenausbreitung sowie senkrecht zur Tropfenkette.
Die Genauigkeit der Konzentrationsbestimmung mit der linearen RamanSpektroskopie kann für die Flüssigphase mit etwa 3 % und für die Gasphase mit etwa
5 % abgeschätzt werden. Dies ergibt sich aus den Schwankungen der Einzelmeßpunkte
der einzelnen Meßreihen.
6. ZUSAMMENFASSUNG UND AUSBLICK
146
6 Zusammenfassung und Ausblick
In dieser Arbeit wurde eine optische Methode zur Bestimmung der instationären
Konzentrations- und Temperaturprofile innerhalb von Mikrotropfen und in seiner
unmittelbaren Umgebung vorgestellt. Am Beispiel des Desorptionsprozesses von
Acetylen aus Acetontropfen wurde der zeitliche Verlauf der Acetylenkonzentration in
den Tropfen sowie die Konzentration des freigesetzten Acetylens um die Tropfen einer
Tropfenkette gemessen. Dazu wurde die gepulste zweidimensionale RamanSpektroskopie entwickelt, mit der erstenmals die Gaskonzentration zwischen den
Tropfen
einer
Tropfenkette
bestimmt
wurde.
Für
die
Bestimmung
der
Acetylenkonzentration innerhalb der Tropfen wurde ein Auswerteverfahren entwickelt,
mit dem erstmalig eine radiale Gewichtung der Streustrahlung aus den Tropfen
festgestellt werden kann. Damit läßt sich nun die mittlere Konzentration von chemischen
Spezies in den Tropfen bestimmen, bei denen ein Konzentrationsgradient vorliegt.
Mit den Grundlagen der Licht-Streuung begann diese Arbeit in Kapitel 2. Dort wurde
zunächst die Raman-Streuung erklärt und einige allgemeine Anwendungen aufgezeigt.
Des weiteren wurde die Mie-Streuung und die Raman-Streuung an sphärischen Mikropartikeln erläutert. Dies war notwendig, da in sphärischen Mikropartikeln sogenannte
Strukturresonanzen auftreten können, die das Streuspektrum empfindlich beeinflussen.
Das motivierte zur Entwicklung eines Modells zur Bestimmung der radialen
Gewichtung von Streustrahlung, das ebenfalls in diesem Kapitel vorgestellt wurde.
Im dritten Kapitel wurden die Transportprozesse an Mikropartikeln erläutert. Hier
wurde ein theoretisches Modell für die instationäre Energie- und Stoffverteilung
innerhalb der Tropfen vorgestellt. Weiterhin wurden theoretische Ansätze für die
ZUSAMMENFASSUNG UND AUSBLICK
147
Modellierung der Gasphase um verdunstende Mikrotropfen aus der Literatur
zusammengetragen. Dabei wurde deutlich, daß kein vollständiges Modell zur
Beschreibung der Gasphase um die Tropfen einer Tropfenkette existiert. Die
Notwendigkeit der experimentellen Untersuchung wird damit besonders deutlich. Zum
Schluß dieses Kapitels wurden die Begriffe Dampfdruck und Löslichkeit insoweit
erläutert, wie sie zur Diskussion bei der Wahl des Systems Acetylen / Aceton benötigt
wurden.
In Kapitel 4 ging es um die Beschreibung des experimentellen Aufbaus. Nach einer
Übersicht über die gesamte Apparatur wurde auf die Erzeugung der Tropfenkette
eingegangen. Zunächst wurde die Theorie des Strahlzerfalls dargestellt. Danach wurde
ein für diese Arbeit konstruierter Schwingblendengenerator vorgestellt, der einige
Vorteile im Vergleich zu den Standardgeneratoren aufweist. Im weiteren wurden der
optische Aufbau und die Meßdatenerfassung und Auswertung detailliert beschrieben.
Dabei wurde auch die zweidimensionale Spektroskopie erklärt. Den Schluß dieses
Kapitels bilden Beschreibungen von kleineren Nebenaufbauten.
Die Messungen sowie die daraus gewonnenen Ergebnisse wurden in Kapitel 5
dargelegt. Zuerst wurde auf die Messungen der Tropfenphase eingegangen. Für die
Auswertung der Messungen wurden die in Kapitel 2 und 3 erarbeiteten Modelle zur
Bestimmung der radialen Gewichtung der Streustrahlung sowie das für die instationäre
Stoffverteilung innerhalb der Tropfen eingesetzt. Für die radiale Gewichtung der
Streustrahlung wurde eine einfache Sprungfunktion eingesetzt, die die Partikel in
volumengleiche Kerne und Schalen spalten. Kern und Schale wurden dann
unterschiedlich
gewichtet.
Gewichtungsfunktionen
Statt
eingesetzt
der
Sprungfunktion
werden,
die
der
könnten
realen
auch
andere
Gewichtung
der
Streustrahlung etwas näher kommen. Weiterhin kann statt des in dieser Arbeit benutzen
Modells der Stoffverteilung innerhalb der Tropfen eines eingesetzt werden, das die
Konzentration an der Phasengrenzfläche genauer beschreibt. Diese Erweiterung der
Modelle hätte keine qualitative Änderung der in dieser Arbeit erzielten Ergebnisse
gebracht: Erstens wurde festgestellt, daß mehr Streulicht aus den oberflächennahen
Gebieten als aus dem Kern der Tropfen kommt und zweitens wurde der
148
6. ZUSAMMENFASSUNG UND AUSBLICK
Diffusionskoeffizient von Acetylen in Aceton ermittelt. Dieser paßt mit Abschätzungen
überein.
Im zweiten Teil von Kapitel 5 wurde die Messung der Gasverteilung um die Tropfen
vorgestellt. Hierzu wurde die für diese Arbeit entwickelte gepulste zweidimensionale
Spektroskopie eingesetzt: Mit der Anregungsfrequenz der Tropfenerzeugung wurde
auch die Detektion der Streustrahlung getriggert, so daß ganz bestimmte Bereiche der
Tropfenkette selektiv gemessen werden konnten. Unter Berücksichtigung der
Zylindergeometrie der Tropfenkette wurde damit das dreidimensionale Konzentrationsfeld der Gasphase nicht nur in der Nähe der Tropfen, sondern auch zwischen den
Tropfen bestimmt. Am Ende dieses Kapitels wurden Nachweisgrenzen, Auflösungen
und Genauigkeit der eingesetzten Meßmethoden zusammengefaßt.
Die gepulste zweidimensionale Spektroskopie kann verbessert werden, indem eine
Lichtschranke aufgebaut wird, die dann Triggerpulse für die Detektion liefert. In diesem
Fall werden nur Tropfen gemessen, die sich durch ein sehr kleines Beobachtungsvolumen bewegen. Messungen an der Tropfenkette bei größeren Abständen zum
Schwingblendengenerator, bei denen der Abstand zwischen den Tropfen nicht mehr
konstant ist, sind dann möglich. Denkbar sind damit auch Messungen der Gasphase um
die Tropfen eines monodispersen Sprays.
Um den Verdunstungsprozeß von Mikrotropfen vollständig beschreiben zu können,
muß auch das instationäre Temperaturprofil in und um die Tropfen bekannt sein. Dies
kann ebenfalls mit den in dieser Arbeit entwickelten Meßmethoden bestimmt werden.
Die Temperatur der Gasphase kann über die Verteilung der Rotations-Raman-Linien
von z.B. Stickstoff- oder Sauerstoffmolekülen gemessen werden. Das Prinzip dieser
Meßmethode wird in Kapitel 2 beschrieben. Nachteil dieser Meßmethode in
Kombination mit der zweidimensionalen gepulsten Raman-Spektroskopie ist die geringe
Empfindlichkeit. Wie in Kapitel 3 diskutiert, muß gerade bei ortsaufgelösten Messungen
die Abkühlung der Gasphase um die Tropfen schon mehrere 10 K betragen, um für diese
Arbeit meßbar werden zu können. Dazu ist eine Flüssigkeit mit einem großen
Dampfdruck und einer hohen Verdampfungsenthalpie notwendig, z.B. Chlorethan.
Die Temperatur von Wassertropfen kann mittels der Raman-Spektroskopie mit
ausreichender Genauigkeit gemessen werden. Jedoch ist die Abkühlung der Wasser-
ZUSAMMENFASSUNG UND AUSBLICK
149
tropfen trotz hoher Verdampfungsenthalpie wegen des niedrigen Dampfdrucks bei
Raumtemperatur so gering, daß sich die Abkühlung der Gasphase um die Tropfen mit
den in dieser Arbeit eingesetzten Methoden nicht messen läßt. Eine Tropfenlösung aus
Wasser und Chlorethan ist nicht möglich, da sich beide Komponenten nicht ausreichend
mischen. Zusammenfassend muß konstatiert werden, daß noch kein System gefunden
wurde, an dem gleichzeitig die Temperatur und die Konzentration in der Gas- und
Flüssigphase mit der Raman-Spektroskopie gemessen werden kann.
Abschließend läßt sich festhalten, daß mit der gepulsten zweidimensionalen RamanSpektroskopie die Profile der Konzentration und der Temperatur in den Tropfen und in
ihrer unmittelbaren Nähe mit ausreichender Genauigkeit gemessen werden können.
150
ANHANG A
Anhang A
Ramanspektren einiger Substanzen
Einige der im Verlauf der Arbeit gemessenen Ramanspektren werden hier
exemplarisch zusammengestellt. Außer den Luftmessungen (Bild A1) werden alle
Messungen an einer thermostatisierten Küvette durchgeführt. Die Temperatur der
Küvette beträgt bei den meisten Substanzen 25°C und wird bei Atmosphärendruck
gemessen. Lediglich bei den Messungen der Dampfphase vom Ethanol (Bild A6) und
vom Aceton (Bild A4) wird die Küvette auf knapp unterhalb der Siedetemperatur der
jeweiligen Substanz gebracht. Um sicherzugehen, daß sich kein anderes Gas in der
Küvette befindet, wird das Signal des Stickstoffs bis zu dessen verschwinden
beobachtet. Die Luftmessungen (Bild A1) werden ohne Meßkammer durchgeführt.
Die Substanzen werden mit der grünen Linie des Argon-Ionen-Laser (Spectra-Physics,
Modell 2030; λ = 514.5 nm) angeregt. Die Leistung PL des Lasers beträgt wahlweise
1 - 8 W. Der Laserstrahl wird auf eine Strahltaille von etwa 75 µm fokussiert. Das
Streulicht wird in einem Winkel von 90° zur Ausbreitungsrichtung des Laserstrahls mit
einem Öffnungswinkel von 38° registriert. Die Polarisation des Laserstrahls ist
senkrecht zur Detektionsrichtung orientiert. Das gesammelte Streulicht wird auf den
Eintrittsspalt eines Doppelmonochromators (Spex 1403) abgebildet. Die Breite des
Eintrittsspalts beträgt wahlweise 30 - 200 µm. Die geritzten Gitter besitzen eine
Strichzahl von 600 Linien/mm. Damit beträgt die lineare Dispersion 30 cm-1/mm. Die
Zwischenspalten sind permanent geöffnet (5 mm). Vor dem zweiten Zwischenspalt war
ein holographisches Ramanfilter (POC, RHE 514.1D) zur Unterdrückung des elastisch
RAMANSPEKTREN EINIGER SUBSTANZEN
151
gestreuten Lichtes plaziert. Das Raman-Spektrum wird von einer CCD-Kamera (Wright
Instruments, Modell 1; Sensor: EEV P8630, 8.5 x 12.8 mm2, Pixelgröße 22 x 22 µm2)
detektiert, welche mit flüssigem Stickstoff gekühlt wird. Da mit einer Belichtung des
CCD-Sensors nur etwa 200 Wellenzahlen aufgenommen werden kann, müssen für
größeren Spektren mehrere Einzelspektren aufgenommen werden, die sich überlappen
und später zusammengefügt werden. Dies bewerkstelligt eine Software, die auch eine
Korrektur
der
ungleichmäßigen
Ausleuchtung
des
CCD-Sensors
durchführt.
Speicherung und Auswertung der Daten mittels eines PC´s.
Bild A1: Ramanspektrum von Luft (im wesentlichen 78 % Stickstoff und 21 % Sauerstoff).
ANHANG A
152
Intensität / willk. Einheiten
Wasser
H2O
0
0
500
1000
1500
2000
2500
3000
3500
4000
4500
-1
Wellenzahlverschiebung / cm
Bild A2:
Küvettenspektrum von Wasser (H2O; Merk).
Intensität / willk. Einheiten
Acetylen
C2H2
0
0
500
1000
1500
2000
2500
3000
3500
4000
-1
Wellenzahlverschiebung / cm
Bild A3: Küvettenspektrum von Acetylen (C2H2; Messer Griesheim 4.1). Zur besseren
Darstellung wurden die hohen Intensitäten einiger Linien nicht mit dargestellt.
RAMANSPEKTREN EINIGER SUBSTANZEN
153
Intensität / willk. Einheiten
Aceton, C3H6O
oberes Spektrum: Flüssigphase
unteres Spektrum: Dampfphase
0
0
500
1000
1500
2000
2500
3000
3500
-1
Wellenzahlverschiebung / cm
Bild A4: Küvettenspektrum von Aceton (C3H6O; Merk, zur Analyse, 99.5 %):
Flüssigphase (oberes Spektrum), Dampfphase (unteres Spektrum). Dem
Spektrum der Flüssigphase wurde ein Intensitäts-Off set von 1000 hinzugefügt.
Intensität / willk. Einheiten
Acetylen C2H2, gelöst in
Aceton C3H6O
0
0
500
1000
1500
2000
2500
3000
3500
4000
-1
Wellenzahlverschiebung / cm
Bild A5: Küvettenspektrum des Gemisches Acetylen - Aceton (Herst.: siehe Bild A3 und A4).
ANHANG A
154
Intensität / willk. Einheiten
Ethanol, C2H6O
oberes Spektrum: Flüssigphase
unteres Spektrum: Dampfphase
0
0
500
1000
1500
2000
2500
3000
3500
4000
-1
Wellenzahlverschiebung / cm
Bild A6: Küvettenspektrum von Ethanol (C2H5OH; J.T. Baker B.V., zur Analyse, 99.8 %):
Flüssigphase (oberes Spektrum), Dampfphase (unteres Spektrum, mit O2- und N2-Rückständen).
Dem Spektrum der Flüssigphase wurde ein Intensitäts-Off set von 2000 hinzugefügt.
Intensität / willk. Einheiten
Schwefeldioxid, SO2
oberes Spektrum: SO2 gelöst in Wasser
unteres Spektrum: gasförmiges SO2
0
800
1000
1200
1400
1600
1800
2000
-1
Wellenzahlverschiebung / cm
Bild A7: Küvettenspektren von Schwefeldioxid (SO2; Messer Griesheim, > 99.98 %) und von in
Wasser (Hersteller siehe Bild A2) gelöstem Schwefeldioxid. In die Lösung wurde 26.8 mmol/l
Kaliumperchlorat (K Cl O4) eingelöst. Dem Spektrum der Lösung wurde ein Intensitäts-Off set
von 1000 hinzugefügt. Die Intensität des SO2 - Gasspektrums wurde auf 1/150stel reduziert.
RAMANSPEKTREN EINIGER SUBSTANZEN
Tabelle A1:
Detaillierte Unterschriften der Abbildungen mit den Meßbedingungen.
Abbildung
Detaillierte Bildunterschriften mit Meßbedingungen
A1
Ramanspektrum von Luft (im wesentlichen 78 %
Stickstoff und 21 % Sauerstoff). Experimentelle
Bedingungen des Gesamtspektrums: Laserleistung 5 W,
Fokustaille 75 µm, Eintrittsspalt des Monochromators
50 µm,
Belichtungszeit
50 s.
Bedingungen
der
Einzelspektren: Laserleistung 8 W, Fokustaille 120 µm,
Eintrittsspalt des Monochromators 50 µm, Belichtungszeit
30 s. Bei 2293 cm-1 ist die Raman-Linie der Anregung
vom ersten zum zweiten angeregten Schwingungsniveau
zu erkennen.
A2
Küvettenspektrum
von
Wasser
(H2O;
Merk).
Laserleistung 2 W, Fokustaille 75 µm, Eintrittsspalt des
Monochromators
30 µm,
Belichtungszeit
1.8 s,
Temperatur 25°C.
A3
Küvettenspektrum von Acetylen (C2H2; Messer Griesheim
4.1). Laserleistung 2 W, Fokustaille 41 µm, Eintrittsspalt
des Monochromators 200 µm, Belichtungszeit 60 s. Zur
besseren Darstellung wurden die hohen Intensitäten
einiger Linien nicht mit dargestellt.
A4
Küvettenspektrum von Aceton (C3H6O; Merk, zur
Analyse, 99.5 %). Flüssigphase (oberes Spektrum):
Laserleistung 2 W, Fokustaille 75 µm, Eintrittsspalt des
Monochromators
30 µm,
Belichtungszeit
1.8 s,
Temperatur 25°C. Dampfphase (unteres Spektrum):
Laserleistung 7 W, Fokustaille 41 µm, Eintrittsspalt des
Monochromators 200 µm, Belichtungszeit 7 s, Temperatur
58°C. Dem Spektrum der Flüssigphase wurde ein
Intensitäts-Off set von 1000 hinzugefügt.
155
ANHANG A
156
Tabelle A1 (Fortsetzung): Detaillierte Unterschriften der Abbildungen mit den
Meßbedingungen
Abbildung
Detaillierte Bildunterschriften mit Meßbedingungen
A5
Küvettenspektrum des Gemisches Acetylen - Aceton
(Hersteller: siehe Bild A3 und A4). Laserleistung 2 W,
Fokustaille 41 µm, Eintrittsspalt des Monochromators
50 µm, Belichtungszeit 2 s. Zur besseren Darstellung
wurden die hohen Intensitäten einiger Linien nicht mit
dargestellt.
A6
Küvettenspektrum von Ethanol (C2H5OH; J.T. Baker
B.V., zur Analyse, 99.8 %). Dampfphase (unteres
Spektrum, mit O2- und N2-Rückständen): Laserleistung
8 W,
Fokustaille
41 µm,
Eintrittsspalt
des
Monochromators
200 µm,
Belichtungszeit
20 s,
Temperatur 60°C. Flüssigphase (oberes Spektrum):
Laserleistung 2 W, Fokustaille 200 µm, Eintrittsspalt des
Monochromators 50 µm, Belichtungszeit 5 s, Temperatur
25°C. Dem Spektrum der Flüssigphase wurde ein
Intensitäts-Off set von 2000 hinzugefügt.
A7
Küvettenspektren von Schwefeldioxid (SO2; Messer
Griesheim, > 99.98 %) und von in Wasser (Hersteller
siehe Bild A2) gelöstem Schwefeldioxid. Lösung:
Laserleistung 4 W, Fokustaille 120 µm, Eintrittsspalt des
Monochromators
200 µm,
Belichtungszeit
1 s.
Gasförmiges SO2: Laserleistung 7 W, Fokustaille 120 µm,
Eintrittsspalt des Monochromators 30 µm, Belichtungszeit
120 s. In die Lösung wurde 26.8 mmol/l Kaliumperchlorat
(K Cl O4) eingelöst. Dem Spektrum der Lösung wurde ein
Intensitäts-Off set von 1000 hinzugefügt. Die Intensität
des SO2 - Gasspektrums wurde auf 1/150stel reduziert.
KALIBRIERUNG DER MASSENDURCHFLUßREGLER
157
Anhang B
Kalibrierung der Massendurchflußregler
Die angezeigten Werte von Massendurchflußreglern / -messern können vom wahren
Volumenstrom abweichen. Gründe dafür können eine falsch justierte Rückstellfeder des
Regelventils, eine defekte Ventilblende (z.B. durch Korrosion), ein defekter Dichtungssatz oder eine zum Teil verstopfte Gasflußsensorröhre sein. Weiterhin kann der Gaskorrekturfaktor (siehe unten) für ein Gas unbekannt sein. Des weiteren kann es zu einem
nichtlinearen Verhalten zwischen dem wahren Gasfluß und dem angezeigten Wert
kommen (dies wurde jedoch auf eine Anfrage bei der Firma MKS nicht bestätigt). Durch
eine Kalibrierung der Massendurchflußregler / -messer und dem damit ermittelten
Kalibrationsfaktor werden Unsicherheiten bezüglich des Gasflusses eliminiert. Die
Erfahrung zeigte darüberhinaus, daß sich die Kalibrierfaktoren ändern können, wenn die
Gasart gewechselt wird.
Zum leichteren Verständnis der Problematik soll hier die Funktionsweise der
Messung des Massendurchflusses von Gasen bei den eingesetzten Geräten kurz erläutert
werden. Eingesetzt wurden zwei Massenflußmesser der Firma Tylan (Typ FM-380, mit
den Bereichsendwerten 5 und 25 slm 1) und drei Massenflußregler der Firma MKS (Typ
1259C, mit den Bereichsendwerten 10, 100 und 1000 sccm
1
). Das Meßprinzip dieser
Geräte ist die thermische Gasflußmessung. Der Gasfluß teilt sich bei Eintritt in den
1
siehe Fußnote auf S. 106
ANHANG B
158
Durchflußregler / -messer in zwei Ströme. Der erste führt durch die Gasflußsensorröhre
und der zweite durch den Bypass. Durchmesser und Länge beider Wege ist so gewählt,
daß ein laminarer Durchfluß gewährleistet ist. Nach den beiden Wegen werden die
Flüsse wieder zusammengeführt und durchlaufen bei Flußreglern das Regelventil, bevor
sie den Flußregler / -messer verlassen. Die Messung der Gasflüsse durch die
Sensorröhren ist firmenspezifisch.
Beim Massenflußmesser der Firma Tylan sind um die Sensorröhre in einem Abstand
von etwa 1 cm zwei unabhängige Widerstandsdrähte gewickelt. Der erste wird auf einer
konstanten Temperatur gehalten und erwärmt das vorbeiströmende Gas. Dies führt am
zweiten
Widerstandsdraht
zu
einer
meßbaren
Erwärmung,
wobei
die
Temperaturdifferenz ein Maß für den Gasstrom ist (Tylan instruction manual, FM-380
mass flowmeter). Die Ansprechzeit für das Tylan-System beträgt typischerweise 2 s.
Die Flußmessung der Massenflußregler der Firma MKS funktioniert durch Messen
der Leistung, die erbracht werden muß, um die Temperatur im Sensorrohr konstant zu
halten. Diese Leistung ist ein Maß für die durchfließende Gasmenge und aus ihr erhält
man die Regelgröße, die den Fluß durch das Regelventil einstellt. Die Ansprechzeit
dieses Systems beträgt < 5 ms.
Um den einwandfreien Betrieb von Massenflußreglern / -messern zu kontrollieren
oder um sie zu kalibrieren, muß der Fluß eines bestimmten Gases durch die
Regler / Messer selbst gemessen werden. Dazu werden zwei Methoden eingesetzt:
Methode 1: Gasstrommessung unter Nutzung der thermischen Zustandsgleichung für ideale Gase
Das Prinzip dieser Methode beruht in der Füllung eines vorher evakuierten Volumens
durch den Massenflußregler und der Messung der Druckänderung in dem Volumen über
der Zeit. Dazu wird hinter dem Massenflußregler ein Glaskolben (V = 10 l) angebracht
und das gesamte Volumen VK, inclusive der Schläuche, Druckmeßgerät etc., ausgelitert.
Dieses Volumen wird evakuiert (p ≈ 1 mbar), anschließend vom Massenflußregler für
KALIBRIERUNG DER MASSENDURCHFLUßREGLER
159
verschiedene Regelbereiche mit dem entsprechenden Gas befüllt und die Druckänderung ∆p pro Zeitintervall ∆t aufgenommen.
Das Verhältnis zwischen Druck, Volumen und Temperatur wird durch die thermische
Zustandsgleichung für ideale Gase beschrieben. Der Volumenstrom am Ausgang eines
Reglers / Messers ist für den Standarddruck pS und die Standardtemperatur TS ausgelegt
(1 sccm (standard cubic centimeter per minute) = 1 Norm cm3/min bezogen auf
pS = 1013 mbar und TS = 0°C). Damit lautet die Zustandsgleichung
pS ⋅
∆V
∆n
=
⋅ R TS
∆t
∆t
(B1)
mit der Stoffmenge n in mol und der Gaskonstanten R.
Die Befüllung des Gesamtvolumens VK geschieht nicht bei Standarddruck und der
Standardtemperatur, sondern bei der Umgebungstemperatur T und dem Druck p im
Gesamtvolumen. Für die Änderung des Druckes im Gesamtvolumen lautet die
Zustandsgleichung:
∆p
∆n
⋅V K =
⋅R T.
∆t
∆t
(B2)
Eliminiert man ∆n/∆t in Gl. (B1) durch Gl. (B2), erhält man einen Ausdruck, mit dem
der Volumenstrom durch den Regler / Messer durch eine Messung der Druckänderung
im Gesamtvolumen bestimmt werden kann:
V ⋅T
∆p
∆V
V& =
=
⋅ K S.
∆t
∆t
T ⋅ pS
(B3)
Beispiele für die Kalibrierung der Massenstromregler von MKS für die Gase SO2 und N2
werden unten gezeigt und diskutiert.
ANHANG B
160
Methode 2: Gasstrommessung über Blasenwanderung durch ein Glasrohr
Das Prinzip dieser Methode erklärt sich durch
Betrachtung von Bild B1. Der vom Massenstromregler / messer kommende Gasstrom wird kurz vor dem
unteren Ende eines vertikal aufgehängten Glasrohres
seitlich eingeleitet. Am unteren Ende des Rohres befindet
sich ein Gummibalg, der mit einer Lösung aus Wasser
und einem Tensid (Pril) gefüllt ist. Die Innenwand des
Glasrohres sollte sehr glatt sein und eine kleine
Radiustoleranz
aufweisen.
Hierzu
eignen
sich
innengezogene Lampenrohre. Wird durch Drücken des
Gummibalges die Lösung über die Öffnung der
Gaseinleitung gehoben, so bilden sich Blasen, die mit
dem Volumenstrom des Gases nach oben steigen. An der
Außenwand des Rohres befinden sich Markierungen, die
ein vorher bestimmtes Volumen definieren. Durch eine
Messung der Transitzeit, die eine Blase benötigt, um die
Strecke zwischen den Markierungen zu durchlaufen,
erhält man direkt den Volumen- bzw. den Massenstrom
des Gases.
Bild B1:
Seifenblasenanemometer zur Messung von Gasflüssen.
KALIBRIERUNG DER MASSENDURCHFLUßREGLER
161
Vergleich der beiden Methoden
Bei beiden Methoden wird eine Zeitdifferenz gemessen und in den entsprechenden
Volumenstrom umgerechnet. Für beide Methoden wird der Gaskorrekturfaktor nicht
benötigt, sondern kann daraus sogar bestimmt werden.
Nachteil von Methode 1 ist, daß die Druckmessung fehlerbehaftet sein kann.
Außerdem können beim Auslitern des Gesamtvolumens Reste des Wassers in der
Anlage verbleiben und somit die Volumenmessung verfälschen.
Nachteil von Methode 2 kann sein, daß ein verwandtes Gas mit dem Blasenmedium
in Wechselwirkung tritt und die Oberflächenspannung herabsetzt, was möglicherweise
zum Platzen der Blasen führt. In einem solchen Fall kann der Wechsel des
Blasenmediums Abhilfe schaffen.
Insgesamt besitzt Methode 2 durch einen einfachen, übersichtlichen Aufbau Vorteile,
da man mit ihm sehr genau Volumenströme messen kann. Diese Methode wird häufig
bei der Messung der Volumenströme durch Differential-Mobilitäts-Analysatoren (DMA)
angewendet.
Messungen und Diskussion
Nach den beiden oben beschriebenen Methoden werden die Massenstromregler von
MKS mit den Bereichsendwerten 1slm und 100sccm kalibriert. Bild B2 zeigt die
Messungen nach Methode 1 für die Gase N2 und C2H2 (Acetylen). An die Meßwerte
werden Geraden angepaßt. Die Gase N2 und C2H2 zeigen ein lineares Verhalten
zwischen dem gemessenen Gasfluß und dem angezeigten Wert. Anders stellt es sich
beim SO2 (Schwefeldioxid) dar, wie in Bild B3 zu sehen ist. SO2 zeigt ein deutlich
nichtlineares Verhalten. Mit einem Polynom 4. Grades werden die einzelnen Meßwerte
verbunden. Die Gründe für dieses Verhalten konnten nicht geklärt werden. Auch eine
Anfrage bei MKS führte nicht zum Erfolg.
ANHANG B
162
Kalibration des Massenstromreglers
(1slm; MKS) nach Methode 2:
gemessener Volumenstrom / l/min
1,0
N2
C2H2
lin. Regression
0,8
0,6
0,4
0,2
0,0
0
10
20
30
40
50
60
70
80
90
100
80
90
100
Anzeige des Volumenstromreglers / %
90
Kalibration des Massenstromreglers
(100sccm; MKS) nach Methode 2:
gemessener Volumenstrom / ccm/min
80
70
N2
C2H2
lin. Regression
60
50
40
30
20
10
0
0
10
20
30
40
50
60
70
Anzeige des Volumenstromreglers / %
Bild B2: Kalibrationsmessungen der Massenstromregler (MKS; 1slm und
100sccm) nach Methode 2 für die Gase N2 und C2H2.
KALIBRIERUNG DER MASSENDURCHFLUßREGLER
163
Vergleicht man die N2-Messungen nach beiden Methoden, die in einem zeitlichen
Abstand von etwa 3 Jahren gemacht wurden, so fällt auf, daß für denselben
Massenstromregler unterschiedliche Werte gemessen wurden. Dies zeigt, daß sich die
angezeigten Werte mit der Zeit verändern können. Eine Justierung der Rückstellfeder
des Regelventils kann das kompensieren. Eine weitere Kontrolle bzw. Kalibrierung ist
danach trotzdem erforderlich.
Kalibrierung der Massenstromregler nach Methode 1:
gemessener Volumenstrom / l/min
1.0
N2 1slm-Regler
SO2 1slm-Regler
N2100sccm-Regler
SO2 100sccm-Regler
0.8
(
(
(
(
lin. Regression)
Polynom)
lin. Regression)
Polynom)
0.6
0.4
0.2
0.0
0
20
40
60
80
100
Anzeige des Volumenstromreglers / %
Bild A3: Kalibrierungsmessungen der Massenstromregler (MKS; 1slm und
100sccm) nach Methode 1 für die Gase N2 und SO2.
ANHANG B
164
Gaskorrekturfaktoren
Der Gaskorrekturfaktor C wird verwendet, um das Verhältnis der Flußraten ω
verschiedener Gase (indiziert mit 1 und 2) zu beschreiben, die dieselbe Ausgangsspannung eines Flußmeßgerätes erzeugen
ω1
C1
=
.
ω2
C2
(B4)
Die Flußrate eines Gases hängt von deren spezifischer Wärmekapazität cP, Dichte ρ
und molekularen Struktur ab. Für eine gleich bleibende Ausgangsspannung ist die
Flußrate
ω =
const. ⋅S
.
ρ cP
(B5)
Hier ist S der Korrekturfaktor für die molekulare Struktur (s. Tab. B1) und die
Konstante beinhaltet die Geräteparameter.
Tabelle B1: Werte für die molekularen Korrekturfaktoren.
Gas
Einatomiges Gas
S
1.030
(z.B. Ar, He, Xe, ...)
Zweiatomiges Gas
1.000
(z.B. CO, N2, O2, NO, ...)
Dreiatomiges Gas
0.941
(z.B. CO2, N2O, SO2, ...)
Polyatomiges Gas
(z.B. NH3, AsH3, B2H6, C2H6, CH4, H3P, ...)
0.880
KALIBRIERUNG DER MASSENDURCHFLUßREGLER
165
Setzt man Gl. B5 in Gl. B4 ein, wählt für das Gas 2 Stickstoff, setzt Dichte,
spezifische Wärme und molekularen Korrekturfaktor des Stickstoffs in die
entsprechenden Parameter ein, so erhält man den Korrekturfaktor für ein beliebiges Gas:
C =
0.3106 ⋅ S
.
ρ cP
(B6)
Die Indizes für das Gas 1 werden hier weggelassen.
Die Werte für einige Gase sind in Tab. B2 zusammengefaßt.
Tabelle B2: Gaskorrekturfaktoren.
Gas
Symbol
Gaskorrekturfaktor
relativ zu N2
C2H2
0.58
-
1.00
Ammoniak
NH3
0.73
Kohlendioxid
CO2
0.70
Wasserstoff
H2
1.01
Stickstoff
N2
1.00
Stickstoffdioxid
NO2
0.74
Stickstoffoxid
N2O
0.71
Sauerstoff
O2
0.99
Schwefeldioxid
SO2
0.69
Acetylen
Luft
LITERATURVERZEICHNIS
166
Literaturverzeichnis
AND 73
A. Anderson, The Raman effect, Vol. 1 and 2, Marcel Dekker, inc.,
New York (1971 und 1973)
AND 92
K. Anders, N. Roth, A. Frohn, „Operation characteristics of vibrating
orifice generators: the coherence length“, Part. Part. Syst. Chact. 9,
40 - 43 (1992)
ANN 92
K. Annamalai, W. Ryan, „Interactive processes in gasification and
combustion. Part I: Liquid drop arrays and clouds“,
Prog. Energy Combust. Sci. 18, 221 - 295 (1992)
ANT 88
C. Antoine, C. R. 107, 681, 836 (1888)
ARD 90
M. v. Ardenne, G. Musiol, S. Reball, Effekte der Physik und ihre
Anwendungen, Verlag Harri Deutsch, Frankfurt / Main (1990)
ASH 70
A. Ashkin, „Acceleration and trapping of particles by radiation
pressure“ , Phys. Rev. Lett. 24, 156 - 159 (1970);
A. Ashkin, J. M. Dziedzic, „Optical levitation by radiation pressure“,
Appl. Phys. Lett. 19, 283 - 285 (1971);
A. Ashkin, J. M. Dziedzic, „Optical levitation of liquid drops by
radiation pressure“, Science 187, 1073 - 1075 (1975);
A. Ashkin, J. M. Dziedzic, „Feedback stabilization of optically
levitated particles“, Appl. Phys. Lett. 30, 202 - 204 (1976)
ASH 77
A. Ashkin, J. M. Dziedzic, „Observation of resonances in the radiation
pressure on dielectric spheres“, Phys. Rev. Lett. 38, 1351 - 1354
(1977);
LITERATURVERZEICHNIS
167
A. Ashkin, J. M. Dziedzic, „Observation of optical resonances of
dielectric spheres by light scattering“, Appl. Opt. 20, 1803 - 1814
(1981)
ATK 96
P. W. Atkins, Physikalische Chemie, VCH Verlagsgesellschaft mbH,
Weinheim (1996)
BAR 77
D. F. Barbe, S. B. Campana, „Imaging arrays using the charge coupled
concept“, Advances in Image Pick-up and Display 3, 171 - 296 (1977)
BAR 89
J. P. Barton, D. R. Alexander, S. A. Schaub, „Theoretical
determination of net radiation force and torque for a spherical particle
illuminated by a focused laser beam“, J. Appl. Phys. 66, 4594 - 4602
(1989);
J. P. Barton, D. R. Alexander, S. A. Schaub, „Internal fields of a
spherical particle illuminated by a tightly focused laser beam: focal
point positioning effects at resonances“, J. Appl. Phys. 65, 2900 - 2906
(1989);
J. P. Barton, D. R. Alexander, S. A. Schaub,“ Internal and near-surface
electromagnetic fields for a spherical particle irradiated by a focussed
laser beam“, J. Appl. Phys. 64, 1632 - 1639 (1988)
BAY 81
L. P. Bayvel, A. R. Jones, Electromagnetic
Applications, Applied Science, London (1981)
BEA 94
H. D. Beahr, K. Stephan, Wärme- und Stoffübertragung, SpringerVerlag, Berlin (1994)
BEG 93
P. Berg, Entwicklung eines Rechenprogramms zur optischen
Bestimmung von Tropfenabstand und Tropfendurchmesser einer
Tropfenkette,
unveröffentlichte
Studienarbeit,
UniversitätGesamthochschule-Duisburg (1993)
BEN 80
R. E. Benner, P. W. Barber, J. F. Owen, R. K. Chang, „Observation of
structure resonances in the fluorescence spectra from microspheres“,
Phys. Rev. Lett. 44, 475 - 478 (1980)
Scattering
and
ist
168
LITERATURVERZEICHNIS
BER 73
R. N. Berglund, B. Y. H. Liu, „Generation of monodisperse aerosol
standards“, Environ. Sci. Technol. 7, 147 - 153 (1973)
BER 93
L. Bergmann, C. Schaefer, Lehrbuch der Experimentalphysik, Band 3:
Optik, Walter de Gruyter & Co., Berlin New York (1993)
BOH 83
C. F. Bohren, D. R. Huffman, Absorption and Scattering of Light by
Small Particles, Wiley-Interscience, New York (1983)
BOP 27
M. Born, R. Oppenheimer, Ann. d. Phys. 84, 457 - 484 (1927)
BOR 93
M. Born und E. Wolf, Principles of Optics, Pergamon, Oxford, UK
(1993)
BOR 94
M. A. Borchers, Entwurf, Aufbau und Erprobung eines Versorgungssystems für einen Schwingblendengenerator, unveröffentlichte
Studienarbeit, Ruhr-Universität Bochum (1994)
BRA 62
J. Brandmüller, H. Moser, Einführung in die Ramanspektroskopie,
Dr. Dietrich Steinkopff Verlag, Darmstadt (1962)
BRO 81
I. N. Bronstein, K. A. Semendjajew, Taschenbuch der Mathematik,
20. Auflage, Verlag Harri Deutsch, Thun und Frankfurt/Main (1981)
BRO 94
Brockhaus-Enzyklopädie: in 24 Bänden, 19. Auflage, F.A. Brockhaus
GmbH, Mannheim (1986 - 94)
CAM 91
A. J. Campillo, J. D. Eversole, H.-B. Lin, „Cavity quantum
electrodynamic enhancement of stimulated emission in microdroplets“,
Phys. Rev. Lett. 67, 437 - 440 (1991)
CAM 98
Persönliche Mitteilung von A. J. Campillo anläßlich seines Deutschlandbesuchs im September 1998.
CAR 59
H. S. Carslaw, J. C. Jaeger, Conduction of Heat in Solids,
Second Edition, Oxford University Press (1959)
LITERATURVERZEICHNIS
169
CHA 96
R. K. Chang, A. J. Campillo (Ed.), Optical processes in microcavities,
World Scientific, Singapore (1996)
CHE 76
H. Chew, P. J. McNulty, M. Kerker, „Model for Raman and
fluorescent scattering by molecules embedded in small particles“,
Phys. Rev. A 13, 316 - 404 (1976)
CHE 96
G. Chen, Md. M. Mazumder, R. K. Chang, J. C. Swindal, W. P. Acker,
„Laser diagnostics for droplet characterisation: Application of
morphology-dependent resonances“, Prog. Energy Combust. Sci. 22,
163 - 188 (1996)
CHY 76
P. Chylek, J. T. Kiehl, M. K. W. Ko, „Optical levitation and partial
wave resonances“, Phys. Rev. A 18, 2229 - 2233 (1976)
CHY 90
P. Chylek, „Resonance structure of Mie scattering: distances between
resonances“, J. Opt. Soc. Am. A 7, 1609 - 1613 (1990)
CON 84
P. R. Conwell, P. R. Barber, C. K. Rushforth, „Resonant spectra of
dielectric spheres“, J. Opt. Soc. Am. A 1, 62 - 67 (1984)
CON 96
C. S. Connon, D. Dunn-Rankin, „Flow behavior near an infinite
droplet stream“, Experiments in Fluids 21, 80 - 86 (1996)
DAV 98
E. J. Davis, „A history of single aerosol particle levitation“,
Aerosol Sci. Technol. 26, 212 - 254 (1997)
DEM 91
W. Demtröder, Laserspektroskopie, 2. Aufl., Springer-Verlag, Berlin
(1991)
DEV 98
V. Devarakonda, A. K. Ray, T. Kaiser, G. Schweiger, „Vibrating
orifice droplet generator for studying fast processes associated with
microdroplets“, Aerosol Sci. Technol. 28, 531 - 547 (1998)
DEV 98b
V. Devarakonda, B. W. May, A. K. Ray, „Composition distribution
inside evaporating binary microdroplets“, vorgestellt auf der
AAAR ´98, Cincinnati, Ohio (1998);
170
LITERATURVERZEICHNIS
DEV 98c
V. Devarakonda, Physical and chemical processes in microdroplets,
Ph. D. Dissertation, University of Kentucky (1998)
ECK 66
G. Eckhardt, W. G. Wagner, „On the calculation of absolute Raman
scattering cross sections from Raman scattering coefficients“,
J. Mol. Spectrosc. 19, 407 - 411 (1966)
EGG 97
J. Eggers, „Nonlinear dynamics and breakup of free-surface flows“,
Rev. Mod. Phys. 69, 865 - 929 (1997)
ESE 95
C. Esen, T. Kaiser, G. Schweiger, „Experimental study of
polymerization reactions on optically levitated microparticles by
Raman spectroscopy“, J. Aerosol Sci. 26, S285 - S286 (1995);
C. Esen, T. Kaiser, G. Schweiger, „Raman investigation of
photopolymerization reactions of single optically levitated
microparticles“, Appl. Spectrosc. 50, 823 - 828 (1996);
ESE 96
C. Esen, G. Schweiger, „Preparation of monodisperse polymer
particles by photopolymerization“, J. Colloid Interface Sci. 179,
276 - 280 (1996);
C. Esen, T. Kaiser, M. A. Borchers, G. Schweiger, „Synthesis of
spherical microcapsules by photopolymerization in aerosols“,
Colloid Polymer Sci. 275, 131 - 137 (1997)
ESE 97
C. Esen, Herstellung fester sphärischer Mikropartikel durch
Photopolymerisation und deren Charakterisierung, Fortschr. Ber.
VDI, Reihe 3, Nr. 516, VDI-Verlag, Düsseldorf (1997);
C. Esen, G. Schweiger, „Erzeugung von festen Mikropartikeln“,
Angemeldete Patentschrift, Offenlegungsschrift: DE 195 17 363 A1;
C. Esen, G. Schweiger, „Erzeugung und Charakterisierung sphärischer
Polymerpartikel“, Chem. Ing. Tech. 70, 112 - 115 (1998);
C. Esen, G. Schweiger, „Preparation and characterization of spherical
polymer particles“, Chem. Eng. Tech. 21, 36 - 39 (1998)
LITERATURVERZEICHNIS
171
EVE 93
J. D. Eversole, H.-B. Lin, A. J. Campillo, P. T. Leung, S. Y. Liu,
K. Young, „High-precision identification of morphology-dependent
resonances in optical processes in microdroplets“,
J. Opt. Soc. Am. B 10, 1955 - 1968 (1993)
EVE 95
J. D. Eversole, H.-B. Lin, A. J. Campillo, „Input/output resonances
correlation in laser-induced emission from microdroplets“,
J. Opt. Soc. Am. B 12, 287 - 296 (1995)
FUC 59
N. A. Fuchs, Evaporation and droplet growth in gaseous media,
Pergamon Press, Oxford (1959)
FUC 64
N. A. Fuchs, The mechanics of aerosols, Dover Publications,
New York (1964)
FUN 92
K. H. Fung, I. N. Tang, Appl. Spectrosc. 46, 159 (1992)
FUN 94
K. H. Fung, D. G. Imre, I. N. Tang, „Detection limits for sulfates and
nitrates in aerosol particles by Raman spectroscopy“,
J. Aerosol Sci. 25, 479 - 485 (1994)
GAR 61
C. G. B. Garret, W. Kaiser, W. L. Long, „Stimulated emission into
optical whispering modes of speres“, Phys. Rev. 124, 1807 - 1809
(1961)
GOU 85
G. Gouesbet, G. Grehan, B. Maheu, „Scattering of a Gaussian beam by
Mie scatter center using a Bromwich formalism“, J. Optics (PARIS)
16, 83 - 93 (1985)
GOU 94
G. Gouesbet, J. A. Lock, „Rigorous justification of the localized
approximation to the beam shape coefficients in generalized LorenzMie theory. II. Off-axis beams“, J. Opt. Soc. Am A 11, 2516 - 2525
(1994)
GRE 84
W. Greiner, Theoretische Physik, Band 4: Quantenmechanik I, Verlag
Harri Deutsch, Thun, Frankfurt am Main (1984)
172
LITERATURVERZEICHNIS
GRO 97
M. Groß, Konstruktion, Montage und Erprobung eines Plasmalinienfilters zur Reduktion der Plasmalinien eines Argon-Ionen-Lasers,
unveröffentlichte Studienarbeit, Ruhr-Universität Bochum (1997)
GS 87
G. Schweiger, „In-situ determination of the molecular composition of
aerosol particles in a monodispers model aerosol“,
Part. Charact. 4, 67 - 73 (1987)
GS 89
G. Schweiger, „Single microparticle analysis by Raman spectroscopy“,
J. Aerosol Sci. 20, 1621 - 1624 (1989)
GS 90a
G. Schweiger, „Raman scattering on single aerosol particles and on
flowing aerosols: a review“, J. Aerosol Sci. 21, 483 - 509 (1990)
GS 90b
G. Schweiger; „Observation of input and output structural resonances
in the Raman spectrum of a single spheroidal dielectric microparticle“,
Opt. Lett. 15, 156 - 158 (1990)
GS 90c
G. Schweiger, „Observation of morphology dependent resonances
caused by the input field in the Raman spectrum of microparticles“,
J. Raman Spectrosc. 21, 165 - 168 (1990)
GS 90d
G. Schweiger, „Raman scattering on moving microparticles:
calculation and measurement of the first and second moments“,
Aerosol Sci. Technol. 12, 1016 - 1030 (1990)
GS 91a
G. Schweiger, „Radiation pressure effect on light scattering from
optically levitated microparticles“,
J. Opt. Soc. Am. B 8, 174 - 176 (1991)
GS 91b
G. Schweiger, „Raman scattering on microparticles: size dependence“,
J. Opt. Soc. Am. B 8, 1770 - 1778 (1991)
GS 92
G. Schweiger, „Optische Konzentrations- und Temperatur-Messung in
Aerosolen und Sprays“, Chem.-Ing.-Tech. 64, 41 - 47 (1992)
GS 94
G. Schweiger, „Optische Resonatoren aus feinsten Tröpfchen“,
Spektrum der Wissenschaft 11, 110 - 118 (1994)
LITERATURVERZEICHNIS
173
GS 96
G. Schweiger, Vorlesungsskript: Lasermeßtechnik, Ruhr-Universität
Bochum (1996)
GS 97
G. Schweiger, „Untersuchung von Transport- und Reaktionsprozessen
an kleinsten Stoffmengen in der Laserlichtfalle“,
Laser und Optoelektronik 29, 76 - 81 (1997)
HAK 92
H. Haken, H. C. Wolf, Molekülphysik und Quantenchemie,
Springer, Berlin (1992)
HAM 92
Hamamatsu, „Image Intensifiers“, Prospekt (1992)
HAM oJ
Hamamatsu, „Characteristics and applications of microchannel plates“,
Technical Manual RES-0795, ohne Jahresangabe
HAY 82
W. Hayduk, B. S. Minhas; Can. J. Chem. Eng. 60, 295 (1982)
HEC 94
E. Hecht, Optik, Addison-Wesley (Deutschland) GmbH, 3. korrigierter
Nachdruck (1994)
HEI 94
P. Heinrich, Reaktionen elektronisch angeregter zweiatomiger Hydride
im Temperaturbereich von 240 bis 1300 K, Dissertation, RuhrUniversität Bochum, Shaker Verlag Aachen (1994)
HER 91
G. Herzberg, Molecular Spectra and Molecular Structure II: Infrared
and Raman Spectra, Reprint Edition w/corrections, Krieger Publishing
Company, Malabar, Florida (1991)
HID 70
G. M. Hidy, J. R. Brock, The dynamics of aerocolloidal systems,
Pergamon Press, New York (1970)
HIL 84
S. C. Hill, R. E. Benner, C. K. Rushforth, P. R. Conwell, „Structural
resonances observed in the fluorescent emission from small spheres on
substrates“, Appl. Opt. 23, 1680 - 1683 (1984)
HIL 88
S. C. Hill, R. E. Benner, „Morphology-dependent resonances“, in
Optical Effects Associated with Small Particles, P. W. Barber,
R. K. Chang (Eds.), Chap. 1, World Scientific, Singapore (1988)
174
LITERATURVERZEICHNIS
HIL 92
S. C. Hill, R. K. Chang, Nova Science Publisher, New York (1992)
HIN 82
W. C. Hinds, Aerosol Technology: Properties, behavior, and
measurements of airborne particles, Wiley-Interscience Publication,
New York (1982)
HOL 95
J. M. Hollas, Moderne Methoden in der Spektroskopie, Vieweg (1995)
HOC 94
K. Hook, Herstellung von Mikrobohrungen,
Studienarbeit, Ruhr-Universität Bochum (1994)
HSI 88
W.-F. Hsieh, J.-B. Zheng, R. K. Chang, Opt. Lett. 13, 497 (1988)
HUC 94
J. L. Huckaby, A. K. Ray, B. Das, „Determination of size, refractive
index, and dispersion of single droplets from wavelength-dependent
scattering spectra“, Appl. Opt. 33, 7112 - 7125 (1994)
HUL 57
H. C. van de Hulst, Light scattering by small particles, Dover,
New York (1957)
JAC 83
J. D. Jackson, Klassische Elektrodynamik, de Gruyter, Berlin (1983)
KAI 92
T. Kaiser, C. Voßmerbäumer, G. Schweiger, „A new approach to the
determination of fluid phase equilibria: concentration measurements
by Raman spectroscopy“,
Ber. Bunsenges. Phys. Chem. 96, 976 - 980 (1992)
KAI 95
T. Kaiser, G. Roll, G. Schweiger, „Enhancement of the Raman
spectrum of optically levitated microspheres by seeded Nanoparticles“,
J. Opt. Soc. Am. B 12, 281 - 286 (1995)
KAI 96a
T. Kaiser,
C. Esen,
H. Moritz,
M. Borchers,
G. Schweiger,
„Observation of fluorescence background suppression in Raman
scattering on single microparticles“,Ber. Bunsenges. Phys. Chem. 100,
119 - 122 (1996);
T. Kaiser, G. Schweiger, „Verfahren zur Unterdrückung der
Fluoreszens bei der Ramanspektroskopie“, Erteiltes Patent,
Nr. 19 522 999 C1 (1996)
unveröffentlichte
LITERATURVERZEICHNIS
175
KAI 96b
T. Kaiser, Optische Untersuchung von Oberflächeneffekten an
Mikropartikeln, Fortschr. Ber. VDI, Reihe 3, Nr. 452, VDI-Verlag,
Düsseldorf (1996)
KER 69
M. Kerker, The Scattering of light and other electromagnetic
radiation, Academic Press, San Diego (1969)
KER 78
M. Kerker, P. J. Mcnulty, M. Scully, H. Chew, D. D. Cooke,
„Raman and fluorescent scattering by molecules embedded in small
particles: numerical results for incoherent optical processes“,
J. Opt. Soc. Am. 68, 1676 - 1685 (1978);
M. Kerker, S. D. Druger, „Raman and fluorescent scattering by
molecules embedded in sheres with radii up to several multiples of the
wavelength“, Appl. Opt. 18, 1172 - 1179 (1979)
KHA 93
E. E. M. Khaled, S. C. Hill, P. W. Barber, „Scattered and internal
intensity of a sphere illuminated with a Gaussian beam“, IEEE Trans.
Antennas Propagat. 41, 295 - 303 (1993);
E. E. M. Khaled, S. C. Hill, P. W. Barber, D. Q. Chowdhury,
“Near-resonance excitation of dielectric spheres with plane waves and
off-axis Gaussian beams“, Appl. Opt. 31, 1166 - 1169 (1992)
KOE 86
G. König, K. Anders, A. Frohn, „A new light-scattering technique to
measure the diameter of periodically generated moving droplets“,
J. Aerosol Sci. 17, 157 - 167 (1986)
KOL oJ
Die Software zur Konvertierung der Meßdaten vom FITS-Format in
das ASCII-Format wurden von meinen Kollegen Dr. R. Vehring und
Dr. T. Kaiser geschrieben. Für die Überlassung dieser Software
möchte ich mich an dieser Stelle bedanken.
KUE 99
A. Hangkamer-Kühnen, Der Tropfenkettenmonitor, unveröffentlichte
Studienarbeit, Ruhr-Universität Bochum (1999)
LAN 28
G. Landsberg, L. Mandelstam, Naturwiss. 16, 557, 772 (1928);
G. Landsberg, L. Mandelstam, J. Russ. phys. chem. Soc. 60,335 (1928)
176
LITERATURVERZEICHNIS
LAN 76
Landolt-Börnstein, IV. Band Technik, 4. Teil Wärmetechnik, Bandteil c: Gleichgewicht der Absorption von Gasen in Flüssigkeiten:
Absorption in Flüssigkeiten von niedrigem Dampfdruck, Springer
Verlag, Berlin (1976)
LAN 96a
S. Lange, Sphärische Mikropartikeln als Volumenemitter thermischer
Strahlung, Dissertation, Ruhr-Universität Bochum, Shaker Verlag
Aachen (1996)
LAN 96b
S. Lange, H. Moritz, G. Schweiger, „Concentration dependence of the
linear Raman scattering on microdroplets“,
vorgestellt auf der AAAR ´96, Orlando (1996);
H. Moritz, S. Lange, G. Schweiger, „The radial weighting of
concentration profiles inside of microparticles by Raman
spectroscopy“, J. Aerosol Sci. 28, S199 - S200 (1998)
LAN 96c
S. Lange, G. Schweiger, „Structural resonances in the total Ramanand fluorescence-scattering cross section: concentration profile
dependence“, J. Opt. Soc. Am. B 13, 1864 - 1872 (1996)
LAW 82
C. K. Law, H. K. Law, „A d2-law for multicomponent droplet
vaporization and combustion“, AIAA J. 20, 522 - 527 (1982)
LEI 84
A. Leipertz, Temperaturbestimmung in Gasen mittels linearer und
nichtlinearer Raman-Prozesse, Habilitationsschrift, Ruhr-Universität
Bochum (1984)
LEM 97
D. Lemken, Untersuchung der Strahlstabilität eines Schwingblendengenerators, unveröffentlichte Studienarbeit, Ruhr-Universität
Bochum (1997)
LET 85
T. R. Lettieri, R. L. Preston, „Observation of sharp resonances in the
spontaneous Raman spectrum of a single optically levitated
microdroplet“, Opt. Comm. 54, 349 - 352 (1985)
LITERATURVERZEICHNIS
177
LEX 98
Ergebnisse, die ich während eines Forschungsaufenthalts an der
University of Kentucky (Lexington, U.S.A.) in der Arbeitsgruppe von
Prof. Asit K. Ray erzielt habe. An dieser Stelle möchte ich mich
herzlich bei Prof. Ray, seinen Mitarbeitern, Venkat Vijaykumar
Devarakonda, Brian W. May und beim DAAD sowie dem NSF für die
Möglichkeit zu dieser fruchtbaren Kooperation bedanken.
LID 92
D. R. Lide (Ed.), CRC Handbook of Chemistry and Physics,
CRC Press, Boca Raton, Florida (1992)
LIN 90a
H.-B. Lin, J. D. Eversole, A. J. Campillo, „Vibrating orifice droplet
generator for precision optical studies“,
Rev. Sci. Instrum. 61, 1018 - 1023 (1990)
LIN 90b
H.-B. Lin, A. L. Huston, J. D. Eversole, A. J. Campillo, „Doubleresonance stimulated Raman scattering from micrometer-sized
droplets“, J. Opt. Soc. Am. B 7, 2079 - 2089 (1990)
LIN 94
H.-B. Lin, A. J. Campillo, „Cw nonlinear optics in droplet
microcavities displaying enhanced gain“, Phys. Rev. Lett. 73, 2440 2443 (1994)
LIN 95
H.-B. Lin, A. J. Campillo, „Radial profiling of microdroplets using
cavity-enhanced Raman spectroscopy“,
Opt. Lett. 20, 1589 - 1591 (1995)
LIU 88
D. Y. Liu, K. Anders, A. Frohn, „Drag coefficients of single droplets
moving on an infinite droplet chain on the axis of a tube“,
Int. J. Multiphase Flow 14, 217 (1988)
LON 77
D. A. Long, Raman Spectroscopy, McGraw-Hill, New York (1977)
LOR 90
L. Lorenz, „Lysbevægelsen i og uden for en af plane lysbφlger belyst
kulge“, Vidensk. Selsk Skr. 6, 1 - 62 (1890)
MAR 86
E.Mariotte, Traité du mouvement des eaux et des autres corps fluides,
E. Michallet, Paris (1686)
LITERATURVERZEICHNIS
178
MAY 94
F. Mayinger
(Ed.),
Optical
Measurements-Techniques
Applications, Springer-Verlag, Berlin (1994)
and
MCK 93
R. L. McKenzie, „Progress in Laser Spectroscopic Techniques for
Aerodynamic Measurements: An Overview“,
AIAA 31, No. 3, 465-477 (1993)
MEL 89
C. A. Melendres, A. Narayanasamy, V. A. Maroni, R. W. Siegel,
„Raman spectroscopy of nanophase TiO2“,
J. Mater.Res. 4, 1246 - 1250 (1989)
MEL 95
Melles Griot GmbH, Bensheim, Deutschland, Katalog (1995/96)
MES 76
A. Messiah, Quantenmechanik, Band 1, Walter de Gruyter, Berlin
(1976);
A. Messiah, Quantenmechanik, Band 2, Walter de Gruyter, Berlin
(1985);
MIE 08
G. Mie, „Beiträge zur Optik trüber Medien speziell kolloidaler
Metallösungen“, Ann. Phys. 25, 377 - 445 (1908)
MKS 93
MKS, Betriebsanleitung „Massendurchflußmesser, Typ 258C/1258C/
2258C, Massendurchflußregler Typ 1259C/2259C“; MKS - Prospekt,
„Gasflüsse, Messen-Regeln-Mischen“ (1993)
MOO 95
H.-J. Moon, G.-H. Kim, Y.-S. Lim, C.-S. Go, J.-H. Lee, J.-S. Chang,
„Liquid microdroplet generator with glass orifice“,
Rev. Sci. Instrum. 66, 3030 - 3033 (1995)
MOR 29
P. M. Morse, Phys. Rev. 34, 57 - 64 (1929)
MOR 92
H. Moritz, Untersuchung der Möglichkeit elektrischer Feldmessung
mittels laserinduzierter Fluoreszenz an CO-Molekülen, Diplomarbeit,
Ruhr-Universität Bochum, Inst. f. Experimentalphysik V (1992)
MOR 94
H. Moritz, P. Heinrich, R. Vehring, G. Schweiger, „Raman
spectroscopic investigation of the isomerisation of HSO3- in
microdroplets“, vorgestellt auf der AAAR ´94, Los Angeles (1994)
LITERATURVERZEICHNIS
179
MOR 95
H. Moritz, P. Heinrich, R. Vehring, G. Schweiger, „Experimental
investigation of concentration gradients in microparticles“,
vorgestellt auf der AAAR ´95, Pittsburgh (1995)
MOR 96a
H. Moritz, R. Vehring, G. Schweiger, „Investigation of the desorption
of acetylene from acetone microparticles“,
J. Aerosol Sci. 27, S517 - S518 (1996)
MOR 96b
H. Moritz, R. Vehring, G. Schweiger, „Untersuchung schneller Stoffund Wärmetransportprozesse an Mikrotropfen mittels der linearen
Raman-Spektroskopie“, vorgestellt auf der SPRAY ´96, Bremen
(1996)
MOR 97
H. Moritz, G. Schweiger, „A novel technique to measure the gas
composition near the surface of microdroplets“, J. Aerosol Sci. 28,
S441 - S442 (1997);
H. Moritz, R. Vehring, G. Schweiger, „Pulsed 2-dimensional Raman
spectroscopy on droplets“, vorgestellt auf der AAAR ´97, Denver
(1997);
H. Moritz, G. Schweiger, „Gepulste Raman-Spektroskopie: Eine neue
Technik zur Ermittlung der Gaszusammensetzung in unmittelbarer
Nähe von Mikrotropfen“, vorgestellt auf der SPRAY ´97, DLR
Lampoldshausen (1997);
H. Moritz, G. Schweiger, „Meßtechnik zur Untersuchung transienter
Transportprozesse in Mehrphasensystemen: Die Gaszusammensetzung
in unmittelbarer Nähe der Oberfläche von Mikrotropfen“, vorgestellt
auf dem Workshop Meßtechnik für stationäre und transiente
Mehrphasenströmungen im Forschungszentrum Rossendorf (1997);
MOR 97b
H. Moritz, S. Lange, G. Schweiger, „The radial weighting of
concentration profiles inside of microdroplets by Raman
spectroscopy“, J. Aerosol Sci. 28, S199 - S200 (1997)
180
LITERATURVERZEICHNIS
MOR 98
H. Moritz, G. Schweiger, „Investigation of the gas composition near
the surface of microdroplets by pulsed 2-D Raman spectroscopy“,
vorgestellt auf der PARTEC 98, 7th European Symposium Particle
Characterisation, Nürnberg (1998);
H. Moritz, T. Kaiser, R. Vehring, G. Schweiger, „Untersuchung
schneller Transportvorgänge an Mikrotropfen“, vorgestellt auf der
internen Arbeitssitzung des GVC-Fachausschusses „Mehrphasenströmungen“, VDI-Gesellschaft und Chemieingenieurwissenschaften
(1998)
MUS 96
J. Musick, J. Popp, M. Trunk, W. Kiefer, „Polymerisation and
copolymerisation reaction observed in optically levitated aerosol
particles“, J. Aerosol Sci. 27, S561 - S562 (1996)
NAK 78
K. Nakanishi; Ind. Eng. Chem. Fundam. 17, 253 (1978
ORM 90
M. Orme, E. P. Muntz, „The manipulation of capillary stream breakup
using amplitude-modulated disturbance: a pictorial and quantitative
representation“, Phys. Fluids A 2, 1124 - 1140 (1990)
OWE 81
J. F. Owen, P. W. Barber, P. B. Dorain, R. K. Chang, „Enhancement of
fluorescence by microstructure resonances of a dielectric fiber“,
Phys. Rev. Lett. 47, 1075 - 1078 (1981)
OWE 82
J. F. Owen, R. K. Chang, P. W. Barber, „Morphology-dependent
resonances in Raman scattering, fluorescence emission, and elastic
scattering from micro particles“,
Aerosol Sci. Technol. 1, 293 - 302 (1982)
PCO 90
PCO Computer Optics, „Dynamisches Verhalten
Bildverstärkern“, Interner Bericht 14 (1990)
PCO 93a
PCO Computer Optics, Operating Instrictions: IRO - Intensified Relay
Optics, Kelheim, Deutschland (1993);
PCO Computer Optics, Zusatzanleitung zur IRO
von
MCP-
LITERATURVERZEICHNIS
181
PCO 93b
PCO Computer Optics, „Optische Abbildung
Tandemanordnung“, Interner Bericht 15 (1993)
mit
einer
PLA 34
G. Placzek, „Rayleigh-Streuung und Raman-Effekt“, in: Handbuch der
Radiologie, Ed. E.Marx, 2. Aufl., Bd. VI, Teil 2, 205 - 374 (1934)
PLA 49
J. Plateau, Acad. Sci. Bruxelles Mém. 16, 3 (1849)
POP 98
J. Popp, M. Lankers, M. Trunk, I. Hartmann, E. Urlaub, W. Kiefer,
„High-precision determination of size, refractive index, and dispersion
of single microparticles from morphology-dependent resonances in
optical processes“, Appl. Spectrosc. 52, 284 - 291 (1998)
QIA 86
S.-X. Qian, J. B. Snow, H.-M. Tzeng, R. K. Chang, „Lasing droplets:
high-lightning the liquid-air interface by laser emission“,
Science 231, 486 - 488 (1986)
QIA 86b
S.-X. Qian, R. K. Chang, „Multi-order Stokes emission from
micrometer-sized droplets“, Phys. Rev. Lett. 56, 926 - 929 (1986)
RAM 28
C. V. Raman, K. S. Krishnan, „A new type of secondary radiation“,
Nature 121, 501-502 (1928);
C. V. Raman, „A change of wave-length in light scattering“,
Nature 121, 619 (1928);
C. V. Raman, „A new radiation“, Indian J. Phys. 2, 387 (1928);
C. V. Raman, K. S. Krishnan, „The optical analogue of the Compton
effekt“, Nature 121, 711 (1928)
C. V. Raman, K. S. Krishnan, Indian J. Phys. 2, 399 (1928);
C. V. Raman, K. S. Krishnan, Proc. Roy. Soc., Lond. 122, 23 (1929)
RAM 88
R. Rambau, G. Schweiger, „Numerical results on Raman scattering by
spherical aerosol particles“, J. Aerosol Sci. 19, 829 - 831 (1988)
RAS 94
S. D. Rassat, E. J. Davis, „Temperature measurement of single
levitated microparticles using Stokes/anti-Stokes Raman intensity
ratios“, Appl. Spectrosc. 48, 1498 - 1505 (1994)
182
LITERATURVERZEICHNIS
RAY 78
J. W. S. Rayleigh (Lord), „On the instability of jets“, Proc. London
Math. Soc. 10, 4 - 13 (1878)
RAY 80
A. K. Ray, E. J. Davis, „Heat and mass transfer with multiple particle
interactions. Part I: Droplet Evaporation“,
Chem. Eng. Commun. 6, 61 - 79 (1980)
RAY 91
A. K. Ray, A. Souyri, E. J. Davis, T. M. Allen, „Precision of light
scattering techniques for measuring optical parameters of
microspheres“, Appl. Opt. 30, 3974 - 3983 (1991)
RAY 95
A. K. Ray, R. Nandakumar, „Simultaneous determination of size and
wavelength-dependent refractive indices of thin-layered droplets from
optical resonances“, Appl. Opt. 34, 7759 - 7770 (1995)
RAY 95b
A. K. Ray, S. Venkatraman, „Binary activity coefficient from
microdroplet evaporation“, AIChE J. 41, 938 - 947 (1995)
RAY 98a
A. K. Ray, V. Devarakonda, „Evaporation of multicomponent
microdroplets of volatile constituents“, J. Aerosol Sci. 29, S585 - S586
(1998)
RAY 98b
A. K. Ray, H. Tu, „Determination of unsteady state evaporation and
growth rates of binary microdroplets from time-dependent light
scattering“, J. Aerosol Sci. 29, S1321 - S1322 (1998)
REI 77
G. Reischl, W. John, W. Devor, J. Aerosol Sci. 8, 55 (1977)
REI 86
R. C. Reid, J. M. Prausnitz, B. E. Poling, The Properties of Gases and
Liquids, 4. Edition, McGraw-Hill, New York (1986)
ROL 98
G. Roll, T. Kaiser, S. Lange, G. Schweiger, „Ray interpretation of
multipole fields in spherical dielectric cavities“,
J. Opt. Soc. Am. A 15, ? - ? (1998)
RUC 90
B. Ruck, Lasermethoden in der Strömungsmeßtechnik, AT-Fachverlag
GmbH, Stuttgart (1990)
LITERATURVERZEICHNIS
183
SAN 98
P. J. Santangelo, I. M. Kennedy, „Demonstration of droplet size and
vaporisation rate measurements in the near field of a two phase jet
using droplet lasing spectroscopy“, J. Aerosol Sci. 29, S387 - S388
(1998)
P. J. Santangelo, D. Flowers, I. M. Kennedy, „Demonstration of
droplet size and vaporisation rate measurements in the near field of a
two phase jet using droplet lasing spectroscopy“, erscheint in Appl.
Opt.;
P. J. Santangelo, I. M. Kennedy, „Droplet lasing spectroscopy applied
to droplet stream flames“, erscheint in Combustion and Flame
SCH 64
J. M. Schneider, C. D. Hendricks, „Source of uniform-sized liquid
droplets“, Rev. Sci. Instrum. 35, 1349 - 1350 (1964)
SCH 79
H. W. Schröter, H.W. Klöckner, „Raman scattering cross sections in
gases and liquids“, in: A. Weber (Ed.) Raman spectroscopy of gases
and liquids, Chap. 4, 123-166, Springer Verlag, Berlin (1979)
SCH 81
A. W. Schroetter, „Raman and infrared spectroscopic techniques for
remote analysis of the atmosphere“, in: R.J.H. Clark, R.E. Hester
(Hrsg.), Advances in infrared and Raman spectroscopy, Vol. 8,
Heyden, London (1981)
SCH 93
K. Schaschek, J. Popp, W. Kiefer, „Morphology dependent resonances
in Raman spectra of optically levitated microparticles: Determination
of radius and evaporation rate of single glycerol/water droplets by
means of internal mode assignment“,
Ber. Bunsenges. Phys. Chem. 97, 1007 - 1011 (1993)
SCH 94
W. Schmidt, Optische Spektroskopie, VCH, Weinheim (1994)
SCH 95
B. Schrader, Infrared and Raman Spectroscopy, VCH, Weinheim
(1995)
SER 90
A. Serpengüzel, G. Chen, R. K. Chang, „Stimulated Raman scattering
of aqueous droplets containing ions: concentration and size
determination“, Part. Sci. and Technol. 8, 179 - 189 (1990)
184
LITERATURVERZEICHNIS
SIL 94
M. A. Silverman, D. Dunn-Rankin, „Experimental investigation of a
rectilinear droplet stream flame“,
Combust. Sci. Technol. 100, 57 - 73 (1994)
SME 23
A. Smekal, „Zur Quantentheorie der Dispersion“,
Naturwissenschaften 43, 873 (1923)
SNO 85
J. R. Snow, S.-X. Qian, R. K. Chang, „Stimulated Raman scattering
from individual water and ethanol droplets at morphology-dependent
resonances“, Opt. Lett. 10, 37 - 39 (1985)
SPE 81
Spex Industries GmbH, Instruction Manual:
Spectrometer, Grasbrunn, Deutschland (1981)
SPE 87
Spectra-Physics, Instruction Manual: Model 2030, High Power Ion
Laser, Mountain View, USA (1987)
STR 41
J. A. Stratton, Electromagnetic Theory, McGraw-Hill, New York
(1941)
THU 84
R. Thurn, W. Kiefer, “Raman-microsampling technique applying
optical levitation by radiation pressure“,
Appl. Spectrosc. 38, 78 - 83 (1984);
THU 85
R. Thurn, W. Kiefer, „Observation of structural resonances in the
Raman spectra of optically levitated dielectric microspheres“,
J. Raman Spectrosc. 15, 411 - 413 (1984);
R. Thurn, W. Kiefer, „Structural resonances observed in the
spontaneous Raman spectrum of optically levitated liquid droplets“,
Appl. Opt. 24, 1515 - 1519 (1985)
TOB 71
M. C. Tobin, Laser Raman Spectroscopy, John Wiley & Sons, Inc. ,
New York (1971)
Model
1403,
LITERATURVERZEICHNIS
185
TSI 82
TSI Inc., Operation Manual: Model 3450, Cleveland, USA;
R. J. Remiarz, J. K. Agarwal, E. M. Johnson, „Improved polystyrene
latex and vibrating orifice monodisperse aerosol generator“,
TSI Quarterly 8, 3 - 12 (1982)
TU 98
H. Tu, V. Devarakonda, A. K. Ray, T. Kaiser, G. Schweiger,
„Determination of complex refractive indices from elastic scattering
spectra from evaporating microdroplets“, vorgestellt auf der
AAAR ´98, Cincinnati (1998)
TYL 87
TYLAN, Instruction Manual: FC-280 Mass Flow Controller, FM-380
Mass Flowmeter (1987)
TYN 75
M. T. Tyn, W. F. Calus; J. Chem. Eng. Data 20, 106 (1975)
TZE 84
H.-M. Tzeng, K. F. Wall, M. B. Long, R. K. Chang, „Laser emission
from individual droplets at wavelength corresponding to morphologydependent resonances“, Opt. Lett. 9, 499 - 501 (1984)
TZE 84b
H.-M. Tzeng, K. F. Wall, M. B. Long, R. K. Chang, „Evaporation and
condensation rates of liquid droplets deduced from structure
resonances in the fluorescence spectra“, Opt. Lett. 9, 273 - 275 (1984)
UME 90
A. Umemura, „A theoretical study on the unsteady, interactive
combustion of a linear fuel droplet stream“, Twenty-third Symposium
(International) on Combustion / The Combustion Institute, Pittsburgh,
PA, U.S.A., 1445 - 1453 (1990)
VEH 92
R. Vehring, G. Schweiger, „Optical determination of the temperature
of transparent microparticles“, Appl. Spectrosc. 46, 25 - 27 (1992)
VEH 95a
R. Vehring, H. Moritz, D. Niekamp, P. Heinrich, G. Schweiger,
„Linear Raman spectroscopy on droplet chain: A new experimentell
method for the analysis of fast transport processes and reactions on
microparticles“, Appl. Spectrosc. 49, 1215 - 1224 (1995)
186
LITERATURVERZEICHNIS
VEH 95b
R. Vehring, In Situ Charakterisierung von Aerosolen aus mehreren
chemischen Komponenten mit linearer Raman-Spektroskopie,
Dissertation, Ruhr-Universität Bochum (1995)
VEH 95c
R. Vehring, G. Schweiger, „Threshold of stimulated Raman scattering
in microdroplets“, J. Aerosol Sci. 26, S235 - S236 (1995)
R. Vehring, „Linear Raman spectroscopy on aqueous aerosols:
Influence of nonlinear effects on detection limits“,
J. Aerosol Sci. 29, 65 - 79 (1998)
VEH 97
R. Vehring, C. L. Aardahl, E. J. Davies, G. Schweiger, D. S. Covert,
„Electrodynamic trapping and manipulation of particle clouds“,
Rev. Sci. Instrum. 68, 70 - 78 (1997)
VEH 98
R. Vehring, C. L. Aardahl, G. Schweiger, E. J. Davies, „The
characterization of fine particles originating from an uncharged
aerosol: size dependence and detection limits for Raman analysis“,
J. Aerosol Sci. 29, 1045 - 1061 (1998)
VEL 98
N. Velesco, G. Schweiger, „Calculation of inelastic scattering on large
aerosol particles by using the geometrical optics approximation“,
eingereicht bei Appl. Opt. (1998)
VES 97
T. Vesala, M. Kulmala, R. Rudolf, A. Vrtala, P. E. Wagner, „Models
for condensational growth and evaporation of binary particles“,
J. Aerosol Sci. 28, 565 - 598 (1997)
VOß 94
C. Voßmerbäumer, Ein optisches Verfahren zur Untersuchung
kohärenter Strukturen in freien Gasstrahlen, Dissertation, RuhrUniversität Bochum (1994)
WAL 62
G. E. Walrafen, „Raman spectral studies of the effects of electrolytes
on water“, J. Chem. Phys. 36, 1035 - 1042 (1962)
WAL 88
P. Walzel, „Spraying and Atomizing of Liquids“, in: Ulmann´s
Encyclopedia of Industrial Chemistry, 5th Ed., Vol. B2 ,VCH
Weinheim (1988)
LITERATURVERZEICHNIS
187
WEB 31
C. Weber, „Zum Zerfall eines Flüssigkeitsstrahls“,
Z. angew. Math. Mech. 11, 136 - 154 (1931)
WEB 79
A. Weber (Ed.), Raman Spectroscopy of Gases and Liquids, SpringerVerlag, Berlin (1979)
WEI 98
Persönliche Mitteilung von Dipl.-Phys. Thomas Weigel (1998)
WEL 81
D. C. Wells, E. W. Greisen, R. H. Harten, „FITS: A flexible image
transport system“, Astron. Astrophys. Suppl. Ser. 44, 363 - 370 (1981)
WIL 55
C. R. Wilke, P. Chang; AIChE J. 1, 264 (1955)
WIL 77
E. Wilhelm, R. Battino, R. J. Wilcock, „Low-pressure solubility of
gases in liquid water“, Chem. Reviews 77, 219 - 262 (1977)
WOO 71
A. W. Woodhead, G. Eschard, „Microchannel plates and their
applications“, Acta Electronica 14, 181 - 200 (1971)
YAN 91
B. Yang, M. D. Morris, H. Owen, „Holographic notch filter for lowwavenumber Stokes and Anti-Stokes Raman spectroscopy“,
Appl. Spectrosc. 45, 1533 - 1536 (1991);
M. J. Pelletier, R. C. Reeder, „Characterization of holographic bandreject filters designed for Raman spectroscopy“, Appl. Spectrosc. 45,
765 - 770 (1991);
M. M. Carrabba, K. M. Spencer, C. Rich, D. Rauh, „The utilization of
a holographic Bragg diffraction filter for Rayleigh line rejection in
Raman spectroscopy“, Appl. Spectrosc. 44, 1558 - 1561 (1991);
B. J. Chang, „Dichromated gelatin holograms and their applications“;
Opt. Eng. 19, 642 - 648 (1980)
ZHA 89
J.-Z. Zhang, R. K. Chang, J. Opt. Soc. Am. B 6, 151 (1989)
ZHA 93
J.-X. Zhang, P. M. Aker, „Spectroscopic probing of particle
interfaces“, J. Chem. Phys. 99, 9366 - 9375 (1993)