Dunkelwolken: Frostige Kinderstuben der Sterne - Max
Werbung

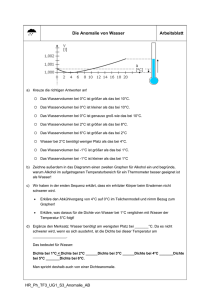
Dunkelwolken Frostige Kinderstuben der Sterne Markus Nielbock Max-Planck-Institut für Astronomie, Heidelberg Die Milchstraße Gebiete aktueller Sternentstehung M 17 – Omeganebel Entfernung: 2.1 kpc (7000 Lj) Sternbild: Schütze Infrarot-Aufnahme ESO/VLT (Hoffmeister et al. 2008) optische Aufnahme Isolierte Dunkelwolken (Globulen) B72 B68 B70 B69 B71 B74 B73 Barnard 68 - Dichteverteilung • sternloser Wolkenkern • Entfernung: 150 pc (500 Lj) • Masse: 3 M • Größe: 0.2 pc (40 000 AE) • gravitativer Kollaps? Alves et al. (2001) Nah-Infrarot-Extinktion Dichte in der Astrophysik Gewöhnlich beschreibt die Dichte ρ, wie viel Masse pro Raumelement vorhanden ist. Wasser hat eine Dichte von ca. 1 kg pro Liter (Kubikdezimeter). Umgerechnet in eine Teilchendichte n sind das 3,3∙1025 Wassermoleküle pro Liter oder 3,3∙1022 Wassermoleküle pro Kubikzentimeter (cm3). Will man die Menge von Teilchen entlang einer Sichtlinie beschreiben (z. B. durch eine Nebelbank), kann man das mittels der Säulendichte N. Sie ist mit der Volumendichte über die Geometrie des Objekts verknüpft. Säulendichte = ρ,n bleiben unverändert, N verdoppelt sich. Die Säulendichte N ist leicht aus der Extinktion zu bestimmen. Da die Form des untersuchten Objekts zunächst unbekannt ist, erfordert die Bestimmung von n Annahmen. So zeigt eine Kugel mit einheitlichem n eine radiale Variation von N. Teilchenanzahl Flächenelement Kollaps einer Globule Überwiegt die Gravitation gegenüber dem inneren Druck, kollabiert die Globule. Damit beginnt die Entwicklung zu einem Stern. James H. Jeans 𝑇 3 𝑐𝑆3 Jeans-Kriterium: 𝑀𝐽 ~ ~ *1877 Ormskirk 𝜌 𝑛 1946 Dorking Ist die Masse des Fragments größer als MJ, so kollabiert es, und zwar in einem Maßstab, der Freifallzeit genannt wird (einige 100000 Jahre). Fragment kollabiert heizt sich auf dehnt sich aus Eine komprimierte Gaskugel (höhere Dichte ρ) heizt sich auf (Luftpumpeneffekt). Dadurch erhöht sich der Gasdruck. Ist die Dichte zu gering, stoppt der Kollaps und kehrt sich um. Aufheizung muss verhindert werden: Kühlung Kollaps eines Wolkenfragments Überwiegt die Gravitation gegenüber dem inneren Druck, kollabiert die Globule. Damit beginnt die Entwicklung zu einem Stern. James H. Jeans 𝑇 3 𝑐𝑆3 Jeans-Kriterium: 𝑀𝐽 ~ ~ *1877 Ormskirk 𝜌 𝑛 1946 Dorking Ist die Masse des Fragments größer als MJ, so kollabiert es, und zwar in einem Maßstab, der Freifallzeit genannt wird (einige 100000 Jahre). Fragment kollabiert Kühlungsprozesse (Energie wird dem System entzogen): • Infrarotstrahlung • Linienstrahlung des Gases nach Stoßanregung C O EPoS – The Earliest Phases of Star formation • Herschel Garantiezeitprogramm (Leitung: O. Krause, MPIA) • Bestimmung der Verteilung von Staubtemperatur und -dichte von 12 nahen und isolierten Wolkenkernen (Launhardt et al. 2013) • Vergleich mit theoretischen Modellen war bislang nicht möglich • Beobachtungen mit Herschel bei 100, 160, 250, 350, und 500 µm • Zusätzliche Daten von bodengebundenen Teleskopen • Vortrag konzentriert sich auf Barnard 68 (Nielbock et al. 2012) Messdaten Nielbock et al. (2012) Elektromagnetische Strahlung Infrarot sichtbares Licht Max Planck *1858 Kiel 1947 Göttingen 1900 Theoretische Beschreibung mit Hilfe der Quantenphysik Nobelpreis 1918 Konstruktion von Temperaturkarten • Über das Planck-Gesetz: Temperatur pro Bildpunkt • räumliche Verteilung der Temperatur des strahlenden Mediums (Staub) • gilt nur für idealisierte Bedingungen • Eigenschaften des Staubs (z.B. Form, Korngröße) spielen eine Rolle • Temperatur nicht unabhängig von der Dichte Nielbock et al. (2012) • Voraussetzung: nur eine Temperatur entlang Beobachtungsrichtung • unrealistisch, gilt nur am Rand • Die ermittelten Größen sind daher die Mittelwerte entlang der Beobachtungsrichtung. Modellierung mittels Ray-Tracing • Berechnung für Punkte entlang „Strahlen“ durch das Objekt • Temperatur und Dichte werden für jeden Punkt gleichzeitig berechnet • Iterativ mit vorgegebenen Anfangsbedingungen für Dichteverteilung und Randwerte • Annahme: radiale Verteilung entlang Himmelsebene = entlang Beobachtungsrichtung ΔnH nout = const Tout = const 3D-Datenkubus: • 100 Zellen entlang Sichtlinie • (10”)3 pro Zelle • entspricht (1500 AE)3 ΔTd 𝑛𝐻 𝑟 = 𝑛0 𝑟0 𝑟02 +𝑟 2 𝜂 + 𝑛𝑜𝑢𝑡 Modellierung mittels Ray-Tracing Ergebnisse: Nielbock et al. (2012) • kalter, dichter Kern • Staubtemperatur nimmt zum Rand hin zu, Dichte nimmt ab (erstmals gemessen) • zentrale Temperatur: 8 K, extern geheizt • Theoretische Berechnungen qualitativ bestätigt • Jeans-Kriterium für Kollaps nicht erfüllt Modellierung mittels Ray-Tracing • radiale Verteilung der Temperatur und der Dichte • relativ flache Verteilung im Zentrum • starker Abfall weiter Außen • Theorie postuliert: nH ~ r -2 • Befund: nH ~ r -3.5 deutet auf Herkunft aus einem Wolkenfilament hin (Ostriker 1964) Nielbock et al. (2012) Sterne entstehen in Wolkenfilamenten B68 Sterne entstehen in Wolkenfilamenten André et al. (2010) Hennemann et al. (2012) ESA/Herschel/Hobys-Konsortium Externe Beleuchtung • galaktisches Strahlungsfeld heizt Globule • Infrarotstrahlung der Milchstraße • Emission der erwärmten Globule asymmetrisch • ungleichförmige Beleuchtung durch gal. Ebene • Temperatur dort am höchsten • naher Stern könnte ebenfalls zur Beleuchtung beitragen • weitere Beobachtungen nötig Zusammenfassung • Sternentstehung beginnt in Dunkelwolken. • Sterne entwickeln sich aus Wolkenkernen (Globulen), die kalt und dicht genug sind. • Herschel ermöglichte zum ersten mal die zuverlässige Bestimmung der Temperatur und der Dichte des Staubs einer Globule, Barnard 68. • Zum ersten mal wurde der Temperaturverlauf experimentell bestimmt. • Sie reicht von 8 K im Zentrum bis zu 20 K am Rand. • Theoretische Vorhersagen wurden zumindest qualitativ bestätigt. • Die Dichte nimmt jedoch nach außen schneller ab als erwartet. • Dichteverlauf deutet auf eine Herkunft aus einem Wolkenfilament hin. • B68 wird von Außen durch das umgebende Strahlungsfeld geheizt. • Heizung scheint nicht von allen Seiten gleich stark zu sein: Anisotropie • Die Hauptheizquelle muss noch durch geeignete Messungen ermittelt werden. Kollisionsszenario Alves et al. (2001) B68 B69 B71 Burkert & Alves (2009)