Netzwerke und Schaltungen I

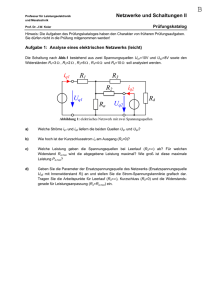
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Name, Vorname
Lösung Nr. 2
Testat
Besprechung: 30.09.2008
Abgabe:
07.10.2008
Lösung Aufgabe 1: Prinzip eines Tintenstrahldruckers
a) Mit zunehmender Spannung UL wächst die Stärke des elektrischen Feldes EL zwischen Düse und
Ringelektrode. Daher werden zunehmend Ladungen im Tintentröpfchen getrennt und es verbleibt
beim Abreissen des Tröpfchens vom Druckkopf mehr negative Ladung im Druckkopf (s. Fig. 6). Folglich steigt die resultierende Ladung im Tintentröpfchen bei zunehmender Spannung UL.
G
EL
- - - -
-
-
+
++
+
+
++
+
Fig. 6: Tintentröpfchen beim Austritt aus dem Druckkopf
b) Das aufgeladene Tröpfchen durchläuft höchstens die Spannung UL. Somit gilt für die Zunahme der
kinetischen Energie:
ΔEkin ≤ q ⋅ U L = 4.5 ⋅ 10−13 C ⋅ 200V = 9 ⋅ 10−11 J
Um die anfängliche kinetische Energie zu berechnen, muss zuerst die Masse des Teilchens berechnet
werden. Diese ergibt sich durch das Kugelvolumen V = 4 π r 3 / 3 des Tröpfchens multipliziert mit dessen
Dichte ρ :
m=
4
4
⋅ π ⋅ r 3 ⋅ ρ = ⋅ π ⋅ (20 ⋅ 10−6 m)3 ⋅ 1.1 ⋅ 103 kg/m3 = 3.686 ⋅ 10−11 kg
3
3
Die anfängliche kinetische Energie berechnet sich mit der bekannten Beziehung
Ekin ,0 =
1
1
⋅ m ⋅ v0 2 = ⋅ 3.686 ⋅ 10−11 kg ⋅ (17m/s) 2 = 5.326 ⋅ 10−9 J .
2
2
Die relative Änderung der kinetischen Energie berechnet sich aus dem Verhältnis der Änderung zur
anfänglichen kinetischen Energie:
ΔEkin
9 ⋅ 10 −11 J
=
⋅ 100% = 1.7% .
Ekin
5.326 ⋅ 10−9 J
Diese minimale Zunahme ist unwesentlich und wird im Folgenden vernachlässigt.
Anmerkung: die maximal mögliche kinetische Energie beim Erreichen der Ringelektrode beträgt (unter
Vernachlässigung von Reibung, Gravitation usw.) Ekin,1 = Ekin,0 + q · UL = 5.42 nJ was einer Geschwindigkeit des Tintentröpfchens von v1 = 17.14 m/s entspricht, die relative Änderung der Geschwindigkeit
beträgt 0.8%.
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
c) Im Plattenkondensator ist das elektrische Feld homogen und es gilt EA = UA / d. Die Coulombkraft
wirkt in Richtung der y-Achse und berechnet sich mit Fy = q · EA = q · UA / d. Gemäss der Newtonschen Bewegungsgleichung gilt:
F = m ⋅ ay ⇒ ay =
F q ⋅U A
4.5 ⋅ 10−13 C ⋅ 3000V
=
=
= 4.578 ⋅ 103 m / s 2
−11
m d ⋅ m 0.008m ⋅ 3.686 ⋅ 10 kg
d) Die Zeit, die das Tröpfchen benötigt um den Ablenkkondensator zu durchfliegen, beträgt t1 = s / v0.
In diesem Abschnitt der Bahnkurve wirkt die konstante Beschleunigung ay aus Teilaufgabe c), daher
ändert sich die Geschwindigkeit vy in Richtung der y-Achse. Die Geschwindigkeit in Richtung der xAchse, vx ≈ v0, bleibt konstant. Es resultiert eine parabelförmige Flugbahn des Tintentröpfchens
(Fig. 7) mit
ay ⋅ s2
1
2
y1 = ⋅ a y ⋅ t1 =
2
2
2 ⋅ v0
Im zweiten Teil der Bahnkurve (Gerade), wirkt keine Kraft auf das Tröpfchen (Luftwiderstand und Gravitation werden ja vernachlässigt). Somit bleibt die vertikale Geschwindigkeit vy = ay · t1 = ay · s / v0, die
das Tröpfchen am Ende des Kondensators besitzt, konstant. Die Zeit, die das Tröpfchen vom Kondensatorende bis zum Papier benötigt, beträgt t2 = l / v0:
y p = y1 + v y ⋅ t 2 =
ay ⋅ s2
2 ⋅ v0
2
+
ay ⋅ s l
ay ⋅ s ⎛ s ⎞
⋅ = 2 ⎜ +l⎟
v 0 v0
v0 ⎝ 2 ⎠
Gerade
G
EA
y
yP
y1
Parabel s
x
d
Ablenkkondensator
Papier
UA
s
l
Fig.7: Bahnkurve des Tröpfchens
e) Damit ein 9.0 mm grosser Buchstabe geschrieben werden kann, muss yp = 9.0 mm sein. Auflösen
der Formel aus d) nach l ergibt:
ay ⋅ s ⎛ s ⎞
⎛ s ⎞ v0 ⋅ y p
+ l⎟ = yp ⇒ ⎜ + l ⎟ =
2 ⎜
ay ⋅ s
v0 ⎝ 2 ⎠
⎝2 ⎠
2
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
(17m/s ) ⋅ 0.009m − 0.02m = 1.841cm
s
⇒l =
− =
2 4.578 ⋅ 103 m/s 2 ⋅ 0.02m
2
ay ⋅ s
v0 2 ⋅ y p
2
f) Für die Flugweite ∆x benötigt das Teilchen die Zeit t = ∆x / v0. Während dieser Zeit wirkt die Erdbeschleunigung g auf das Teilchen:
2
⎛ Δx ⎞
1
1
1
⎛ 0.06m ⎞
−5
Δy = ⋅ g ⋅ t 2 = ⋅ g ⋅ ⎜ ⎟ = ⋅ 9.81m/s ⋅ ⎜
⎟ = 6.110 ⋅ 10 m .
2
2
2
⎝ 17m/s ⎠
⎝ v0 ⎠
Folglich fällt die Ablenkung aufgrund der Gravitation nicht ins Gewicht.
2
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
Lösung Aufgabe 2: Kompensationsschaltung
a) Weil das elektrische Feld in den betrachteten Bereichen zwischen H und P (0 < x < d1) bzw. zwischen P und Q (d1 < x < d1 + d2) jeweils homogen ist, erhält man für die Beträge der beiden elektrischen Feldstärken: E1 = U1 / d1 und E2 = U2 / d2. Die Kraft auf ein Elektron im Gebiet zwischen H und
P beträgt F1 = e · E1 = e · U1 / d1, zwischenGP und Q wirkt die Kraft F2 = e · E2 = e · U2 / d2. Aufgrund
der negativen Ladung
G des Elektrons zeigt F1 gegen die Richtung des elektrischen Feldes, also in positive x-Richtung; F2 zeigt in negative x-Richtung. Die auf das Elektron wirkende Beschleunigung berechnet sich mit der Newtonschen Bewegungsgleichung,
F1 = m ⋅ a1 ⇒ a1 =
F1 e ⋅ U1 1.602 ⋅ 10−19 C ⋅ 1000V
=
=
= 3.517 ⋅ 1015 m/s 2 ,
−31
m m ⋅ d1 9.104 ⋅ 10 kg ⋅ 0.05m
bzw. als Vielfaches der Erdbeschleunigung g ausgedrückt:
a1 =
a1
3.517 ⋅ 1015 m/s 2
⋅g =
⋅ g = 3.585 ⋅ 1014 ⋅ g .
9.81m/s 2
g
b) Die Zeit berechnet sich aus der bekannten Beziehung für den zurückgelegten Weg bei konstanter
Beschleunigung:
d1 =
1
⋅ a1 ⋅ t12 ⇒ t1 =
2
2 ⋅ d1
2 ⋅ 0.05m
=
= 5.332 ⋅ 10−9 s .
15
2
a1
3.517 ⋅ 10 m/s
Daraus erhalten wir die Geschwindigkeit bei P:
v1 = a1 ⋅ t1 = 3.517 ⋅ 1015 m/s 2 ⋅ 5.332 ⋅ 10−9 s = 1.876 ⋅ 107 m/s .
Die kinetische Energie in P berechnet sich zu
Ekin =
2
1
1
1.602 ⋅ 10−16
⋅ m ⋅ v12 = ⋅ 9.104 ⋅ 10−31 kg ⋅ (1.876 ⋅ 107 m/s ) = 1.602 ⋅ 10−16 J =
eV = 1000eV .
2
2
1.602 ⋅ 10−19
Anmerkung 1: die kinetische Energie lässt sich auch mittels des Energieerhaltungssatzes berechnen,
Ekin = U1 ⋅ e = 1000V ⋅ e = 1000eV ,
d.h. nach dem Durchlaufen der Beschleunigungsspannung von 1 kV besitzt das Elektron die kinetische Energie von 1 keV!
Anmerkung 2: die Berechnung mittels Newton’scher Mechanik ist nur zulässig für Geschwindigkeiten
des Elektrons v << c0 ≈ 3·108 m/s (die relativistische Masse des Elektrons,
M (v) = m
1 − (v / c) ,
2
ist im gegebenen Fall etwa 0.2% grösser als die Ruhemasse).
c) Bis zum Umkehrpunkt U (Fig. 8) wird die kinetische Energie, die das Elektron bei P hatte, in potentielle Energie umgewandelt:
Ekin = E pot ,U = F2 ⋅ s = e ⋅ E2 ⋅ s =
e ⋅U2
⋅s
d2
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
(s bezeichnet den Abstand zwischen P und U, s. Fig. 8). Nach s umgeformt berechnet sich der Abstand des Umkehrpunkts – unter Verwendung von Ekin = U1·e aus Teilaufgabe b) – zu
s=
Ekin ⋅ d 2 U1 ⋅ e ⋅ d 2 U1
1000V
d2 =
=
=
⋅ 8.0cm = 6.67cm .
e ⋅U2
e ⋅U2
U2
1200V
G
E1
G
E2
Fig.8: Elektron im Bereich d1 < x < d1 + d2; beim Umkehrpunkt U verschwindet die Geschwindigkeit
des Elektrons
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
Lösung Aufgabe 3: Feld und Potential eines Kugelkondensators
a) Für das Potential einer Punktladung Q gilt:
ϕ (r ) = ϕ 0 +
Q
4πε 0 ⋅ r
.
(1)
Damit die Ersatzanordnung gültig ist, muss das Potential der inneren Kondensatorelektrode den Wert
+50 V und das der äusseren Elektrode den Wert -30 V annehmen (das Erdsymbol in Fig. 3 in der Aufgabenstellung kennzeichnet das Referenzpotential 0V, die Vorzeichen der Potentiale liegen in dem
dort eingezeichneten Richtungssinn der jeweiligen Quellenspannung begründet). Es muss also gelten:
ϕ (ri ) = ϕ0 +
ϕ (ra ) = ϕ0 +
Q
4πε 0 ⋅ ri
Q
4πε 0 ⋅ ra
= 50V ,
(2)
= −30V .
(3)
Aus diesen zwei Gleichungen lässt sich die unbekannte Ladung Q ermitteln, beispielsweise durch
Subtraktion der Gleichung (3) von Gleichung (2),
ϕ (ri ) − ϕ (ra ) = ϕ0 +
Q
4πε 0 ⋅ ri
ϕ (ri ) − ϕ (ra ) =
− (ϕ0 −
Q
4πε 0 ⋅ ra
) = 50V − ( −30V ) ,
Q ⎛1 1⎞
⎜ − ⎟ = 80V .
4πε 0 ⎝ ri ra ⎠
Nach Q aufgelöst erhalten wir für die äquivalente Punktladung den Wert
Q=
80V ⋅ 4πε 0 ra ⋅ ri
0.1m ⋅ 0.01m
C
=
⋅ 80V ⋅ 4πε 0 =
⋅ 80V ⋅ 4π ⋅ 8.854 ⋅ 10−12
= 9.890 ⋅ 10−11 C .
⎛ 1 1 ⎞ ra − ri
0.1m − 0.01m
Vm
⎜ − ⎟
⎝ ri ra ⎠
b) Zuerst bestimmen wir die Unbekannte φ0 aus Gleichung (1). Dies geschieht z.B. unter Verwendung
von Gleichung (2),
ϕ0 +
Mit Q =
Q
4πε 0 ⋅ ri
= 50V ⇒ ϕ0 = 50V −
Q
4πε 0 ⋅ ri
.
ra ⋅ ri
⋅ 80V ⋅ 4πε 0 erhalten wir für φ0 den Wert
ra − ri
r
0.1m
ϕ0 = 50V − a ⋅ 80V = 50V −
⋅ 80V = −38.889V
ra − ri
0.1m − 0.01m
(dasselbe Resultat würden wir unter Verwendung von Gleichung (3) anstelle von Gl. (2) erhalten).
Folglich lässt sich der gesuchte Radius rp bestimmen, indem Gleichung (1) gleich 0 gesetzt und nach
dem Radius aufgelöst wird,
ϕ (rp ) = ϕ0 +
Q
4πε 0 ⋅ rp
!
= 0V ⇒ rp = −
Q
4πε 0 ⋅ ϕ0
=−
9.890 ⋅ 10−11 C
4π ⋅ 8.854 ⋅ 10−12 C ( Vm ) ⋅ ( −38.889V )
−1
= 2.286cm .
Da das Potential bei P3 -30 V beträgt und folglich, vom Bezugspotential 0V zum Punkt P3 gemessen,
eine elektrische Spannung von +30V anliegt, wird bei der Verschiebung positiver Ladung vom Referenzpotential 0V zu P3 Energie freigesetzt.
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
c) Als Feldarbeit wird die Arbeit bezeichnet, die das elektrische Feld am Teilchen umsetzt und ist für
ein Teilchen der Ladung q von Punkt A nach Punkt B unabhängig vom Weg definiert als:
G G
WFeld , AB = q ⋅ ∫ E ⋅ d s = q ⋅ (ϕ ( A) − ϕ ( B) ) .
B
A
(Sie ist bis auf das Vorzeichen gleich der Arbeit, die vom Teilchen im Feld verrichtet wird.)
Da für die gegebene Anordnung das Potential nur vom Radius r abhängt (s. Gl. (1)), haben P1 und P2
das gleiche Potential. Daher verschwindet sowohl die Differenz der beiden Potentiale wie auch die
Feldarbeit von P1 nach P2.
d) Mit der Formel aus c) erhalten wir:
WFeld , P1 P3 = q ⋅ (ϕ ( P1 ) − ϕ ( P3 ) ) = 2.0 ⋅ 10−11 C ⋅ ( 0V − ( −30V ) ) = 6 ⋅ 10−10 J .
Das positive Vorzeichen bedeutet, dass Energie aus dem Feld an das Teilchen übertragen wird, d.h.
das Teilchen wird beschleunigt.
Professur für Leistungselektronik
Netzwerke und Schaltungen I
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
Lösung Aufgabe 4: Feldlinien und Potentialflächen
4.1 a) Der, innerhalb der potentialfreien und elektrisch leitfähigen Hülle angebrachte, positiv geladene Körper bewirkt eine Ladungstrennung an der Hülle, d.h. es stellt sich einerseits eine elektrische Feldverteilung zwischen dem Körper und der Innenseite der Hülle und andererseits eine Feldverteilung zwischen der Aussenseite der Hülle und der Erde ein (Fig. 9).
Fig. 9: Feldlinien und Äquipotentiallinien für die Anordnung nach Aufgabe 4.1.a), Spannung zwischen Körper und Erde: 1 kV
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Netzwerke und Schaltungen I
Lösung Nr. 2
4.1 b) Wird die Hülle mit der (elektrisch leitfähigen) Erde verbunden, dann können die Ladungen an der Aussenseite der Hülle abfliessen; übrig bleibt
die Feldverteilung zwischen dem geladenen Körper und der Innenseite der Hülle (Fig. 10).
Fig. 10: Feldlinien und Äquipotentiallinien für die Anordnung nach Aufgabe 4.1.b), Spannung zwischen Körper und Erde bzw. Hülle: 1 kV
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
4.2 a) Einerseits liegen zwei Körper mit entgegengesetzter Ladung vor, daher sind von der positiven Ladung ausgehende und bei der negativen Ladung
endende elektrische Feldlinien zu erwarten. Andererseits verzerrt die Hülle aus Metall das Feldbild, da das resultierende elektrische Feld an der
Oberfläche sehr gut leitfähiger Materialien ausschliesslich eine senkrecht zur Oberfläche stehende Komponente aufweisen kann. Die (ideal) leitfähige metallische Hülle schirmt das elektrische Feld vollständig ab, im Inneren der Hülle verschwindet daher die elektrische Feldstärke (Fig. 11).
+
-
Fig. 11: Feldlinien und Äquipotentiallinien für die Anordnung nach Aufgabe 4.2.a), Spannung zwischen den beiden Körpern: 1 kV
Netzwerke und Schaltungen I
Professur für Leistungselektronik
und Messtechnik
Prof. Dr. J.W. Kolar
Lösung Nr. 2
4.2 b) Innerhalb der Metallhülle erzeugen die beiden entgegengesetzt geladenen Kugeln ein elektrisches Feld, das jedoch von der ideal leitfähigen Hülle vollständig abgeschirmt wird (Fig. 12).
+
-
Fig. 12: Feldlinien und Äquipotentiallinien für die Anordnung nach Aufgabe 4.2.b), Spannung zwischen den beiden Körpern: 1 kV