Netzwerke und Schaltungen II Symmetrierschaltung (mittel)
Werbung

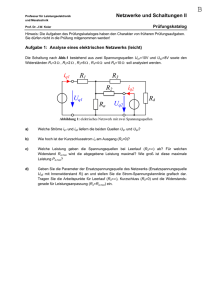
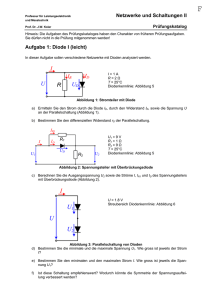
D Professur für Leistungselektronik und Messtechnik Netzwerke und Schaltungen II Prüfungskatalog Prof. Dr. J.W. Kolar Hinweis: Die Aufgaben des Prüfungskataloges haben den Charakter von früheren Prüfungsaufgaben. Sie dürfen nicht in die Prüfung mitgenommen werden! Symmetrierschaltung (mittel) Um bei grossen einphasigen Lasten, wie sie z.B. beim Einsatz von Induktionsöfen grosser Leistung auftreten, eine symmetrische Belastung des Dreiphasennetzes zu erreichen, verwendet man Symmetrierschaltungen nach Fig.1. Die durch den Wirkwiderstand R dargestellte einphasige Belastung nimmt den Strom |I12|=10 A auf und soll durch die zwischen L1 und L2 geschaltete (verlustlose) Drosselspule und den an L2 und L3 angeschlossenen Kondensator in eine für das Dreiphasennetz symmetrische Belastung mit dem Wirkfaktor cos ϕ = 1 umgewandelt werden. Das Dreiphasennetz ist charakterisiert durch die Aussenleiterspannung U=500 V und die Frequenz f=50 Hz Fig.1 : Schaltung zur Symmetrierung einer einphasigen Belastung R des Dreiphasennetzes. Induktivität L und Kapazität C als Symmetriereinrichtung. a) Welchen Effektivwert weisen die Aussenleiterströme auf? (Hinweis: Geben Sie ein vollständiges Zeigerdiagramm der Schaltung (Aussenleiterspannungen, Aussenleiterströme und Strangströme) an, wobei die Zeigerlänge der Strangströme I23 und I31 so zu wählen sind, dass die geforderte Symmetriebedingungen erfüllt sind.) b) Welche Werte müssen die Induktivität L und die Kapazität C für die Symmetrierung haben? c) Durch eine schadhafte Zuleitung wird der Stromfluss durch R unterbrochen (I12 = 0). Geben Sie das dann gültige Zeigerdiagramm und den Effektivwert des Stromes I3 an. d) Durch einen Verschaltungsfehler wird die Kapazität C nicht zwischen L2 und L3, sondern zwischen L1 und L3 geschaltet. Welcher Stromeffektivwert tritt nun für I3 auf? D Netzwerke und Schaltungen II Professur für Leistungselektronik und Messtechnik Prüfungskatalog Prof. Dr. J.W. Kolar Hinweis: Die Aufgaben des Prüfungskataloges haben den Charakter von früheren Prüfungsaufgaben. Sie dürfen nicht in die Prüfung mitgenommen werden! Lösungen: a) I1 = I2 = I3 = I23 = I31 = I12 / b) L = 275.7 mH, C = 36.76 uF c) I3 = I31 = 5.774 A 3 = 5.774 A 2 U12 I23 I31 I3 1 U31 d) I3 = 0 A U2 U1 N U3 U23 3 D Professur für Leistungselektronik und Messtechnik Netzwerke und Schaltungen II Prüfungskatalog Prof. Dr. J.W. Kolar Hinweis: Die Aufgaben des Prüfungskataloges haben den Charakter von früheren Prüfungsaufgaben. Sie dürfen nicht in die Prüfung mitgenommen werden! Unsymmetrische Belastung eines Dreileiternetzes (mittel) Der Wirkwiderstand R=100 Ω und der induktive Blindwiderstand XL=100 Ω sind entsprechend Fig.1 an ein Dreileiternetz (dessen Laststernpunkt nicht mit Erde verbunden ist) mit U=500 V angeschlossen. a) Man ermittle die Aussenleiterströme I1, I2 und I3 und die Phasenwinkel φ1, φ2 und φ3 der zugehörigen Sternspannungen der Speisung ( ≠ Strangspannung). Der Phasenwinkel φ1 ist definiert als φU1 - φI1. (Hinweis: Benutzen Sie das Zeigerdiagramm in Fig.2 um eine anschauliche Lösung zu finden.) b) Welche Leistungen würden 3 Leistungsmesser anzeigen, die jeweils vom Aussenleiterstrom durchflossen werden und die Spannung zwischen dem jeweiligen Aussenleiter und einem künstlichen Sternpunkt messen? c) Die Leistungsaufnahme der Schaltung werde mit der 2-Wattmetter-Methode (Aronschaltung) gemessen. Welche Werte zeigen die Wattmeter an, wenn die Ströme in L1 und L2 und die Spannungen bezogen auf L3 gemessn werden? Welche Anzeige ergibt sich bei Messung der Ströme in L1 und L3 und Spannungsmessung bezogen auf L2? 2 U12 U1 1 U31 Fig.1 : Unsymmetrische Belastung eines Dreileiternetzes. U2 N U3 U23 3 Fig.2 : Spannungen im Dreiphasensystem. D Netzwerke und Schaltungen II Professur für Leistungselektronik und Messtechnik Prüfungskatalog Prof. Dr. J.W. Kolar Hinweis: Die Aufgaben des Prüfungskataloges haben den Charakter von früheren Prüfungsaufgaben. Sie dürfen nicht in die Prüfung mitgenommen werden! Lösungen: a) I1 = 5 A, φ1 = -30° I2 = 9.66 A, φ2 = 45° I3 = 5 A, φ3 = 120° b) P1 = 1250 W P2 = 1972 W P3 = -722 W c) 1) Pi = 1250 W Pii = 1250 W 2) Pi = 2500 W Pii = 0 W → Ptot = P1 + P2 + P3 = 2500 W → Ptot = Pi + Pii = 2500 W → Ptot = Pi + Pii = 2500 W