Blatt 5 Prof. Dr. U. Schollwöck Wintersemester

Theoretische Physik
Thermodynamik und statistische Physik (T4)
Prof. Dr. U. Schollwöck
25. November 2016
Blatt 5
Wintersemester 2016/17
Aufgabe 11: Joule-Thomson Prozess
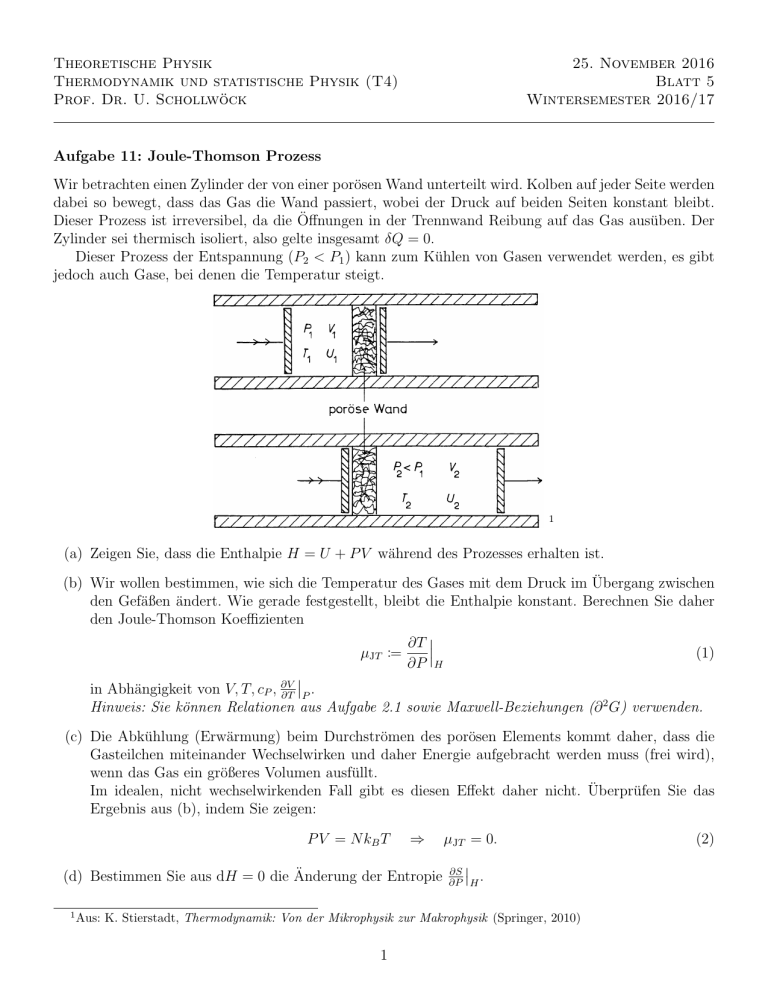
Wir betrachten einen Zylinder der von einer porösen Wand unterteilt wird. Kolben auf jeder Seite werden
dabei so bewegt, dass das Gas die Wand passiert, wobei der Druck auf beiden Seiten konstant bleibt.
Dieser Prozess ist irreversibel, da die Öffnungen in der Trennwand Reibung auf das Gas ausüben. Der
Zylinder sei thermisch isoliert, also gelte insgesamt δQ = 0.
Dieser Prozess der Entspannung (P2 < P1 ) kann zum Kühlen von Gasen verwendet werden, es gibt
jedoch auch Gase, bei denen die Temperatur steigt.
1
(a) Zeigen Sie, dass die Enthalpie H = U + P V während des Prozesses erhalten ist.
(b) Wir wollen bestimmen, wie sich die Temperatur des Gases mit dem Druck im Übergang zwischen
den Gefäßen ändert. Wie gerade festgestellt, bleibt die Enthalpie konstant. Berechnen Sie daher
den Joule-Thomson Koeffizienten
∂T :=
(1)
µJT
∂P H
.
in Abhängigkeit von V, T, cP , ∂V
∂T P
Hinweis: Sie können Relationen aus Aufgabe 2.1 sowie Maxwell-Beziehungen (∂ 2 G) verwenden.
(c) Die Abkühlung (Erwärmung) beim Durchströmen des porösen Elements kommt daher, dass die
Gasteilchen miteinander Wechselwirken und daher Energie aufgebracht werden muss (frei wird),
wenn das Gas ein größeres Volumen ausfüllt.
Im idealen, nicht wechselwirkenden Fall gibt es diesen Effekt daher nicht. Überprüfen Sie das
Ergebnis aus (b), indem Sie zeigen:
P V = N kB T
⇒
(d) Bestimmen Sie aus dH = 0 die Änderung der Entropie
1
µJT = 0.
∂S .
∂P H
Aus: K. Stierstadt, Thermodynamik: Von der Mikrophysik zur Makrophysik (Springer, 2010)
1
(2)
Aufgabe 12: Mischungsentropie
Betrachten Sie ein ideales Gas, beschrieben durch die Gleichungen:
P V = N kB T
und
U = cN kB T,
(3)
wobei die Konstante c komponentenabhängig ist.
(a) Berechnen Sie die Entropie S in Abhängigkeit vom initialen Zustand T0 , V0 , S0 .
Hinweis: Integrieren Sie dS(U, V ).
Sie sollten in dem Ausdruck für die Entropie einen Term t̃ := N kB ln VV0 finden.
Betrachten Sie nun eine Mischung aus unterscheidbaren idealen Gasen. Die Gleichungen 3 gelten für
V
jede Komponente, die Konstanten ci können unterschiedlich sein. Das molare Volumen v0 := N0,ii aller
Komponenten sei am Anfang gleich.
P
(b) Man könnte annehmen, dass der Term t̃ nun die Form N kB ln NVv0 hat, wobei N = Ni .
Zeigen Sie, dass es für die Mischung unterscheidbarer Gase jedoch einen zusätzlichen Term gibt,
die Mischungsentropie“.
”
Die Mischungsentropie soll im Beispiel der Urananreicherung betrachtet werden.
10 Mol Uran(VI)-fluorid (UF6 ) sollen bei konstantem Druck und Raumtemperatur (300K) angereichert
werden. Im Ausgangszustand liege U235 mit einer Häufigkeit von 0.72% vor. Nehmen Sie an, dass der
Rest aus U238 besteht. Am Ende soll 1 Mol UF6 mit 2% U235 vorliegen, sowie 9 Mol UF6 mit entsprechend
niedrigerer Konzentration.
(c) Gehen Sie davon aus, dass sich UF6 wie ein ideales, zweikomponentiges Gas (Gleichungen 3 mit
c = 7/2) verhält. Berechnen Sie die Arbeit, welche zur Isotopentrennung aufgewendet werden
muss, unter der Annahme, dass die Energie des Gases konstant bleibt (dU = 0).
J
Hinweis: NA kB = R ≈ 8.3 molK
.
Aufgabe 13: Freie Energie
(a) Berechnen Sie die freie Energie F = U − T S für ein ideales Gas (Gleichungen 3) in Abhängigkeit
von V(0) , N(0) , T(0) , F0 = F (T0 , V0 , N0 ).
Da die Teilchenzahl nicht konstant gehalten wird, empfiehlt es sich in intensiven Größen
{S, V, U }
(4)
{s, v, u} :=
N
zu rechnen.
Berechnen Sie s(u, v) analog zu Aufgabe 12 (a) und drücken Sie damit die freie Energie aus:
U (T, N ) V
F (T, V, N ) = U − T S = U − T N s
,
.
(5)
N
N
Wir betrachten nun einen Zylinder, in welchem zwei ideale Gase von jeweils einem Mol durch eine
verschiebbare Wand voneinander getrennt sind. Der Zylinder sei abgeschlossen (dN = 0) und befinde
sich in einem Wärmereservoir bei 0◦ C.
(b) Im Fall von konstantem T und N sollte sich die Gleichung aus (a) vereinfachen zu
V
F = const. − N kB T ln .
(6)
V0
Berechnen Sie die Arbeit, welche verrichtet wird wenn die Volumen reversibel von anfangs 10 bzw.
1 Liter zu 6 bzw. 5 Litern geändert werden.
J
Hinweis: Nach wie vor gilt NA kB = R ≈ 8.3 molK
.
2