1. Die Expansion des Kosmos. Hubbles Konstante

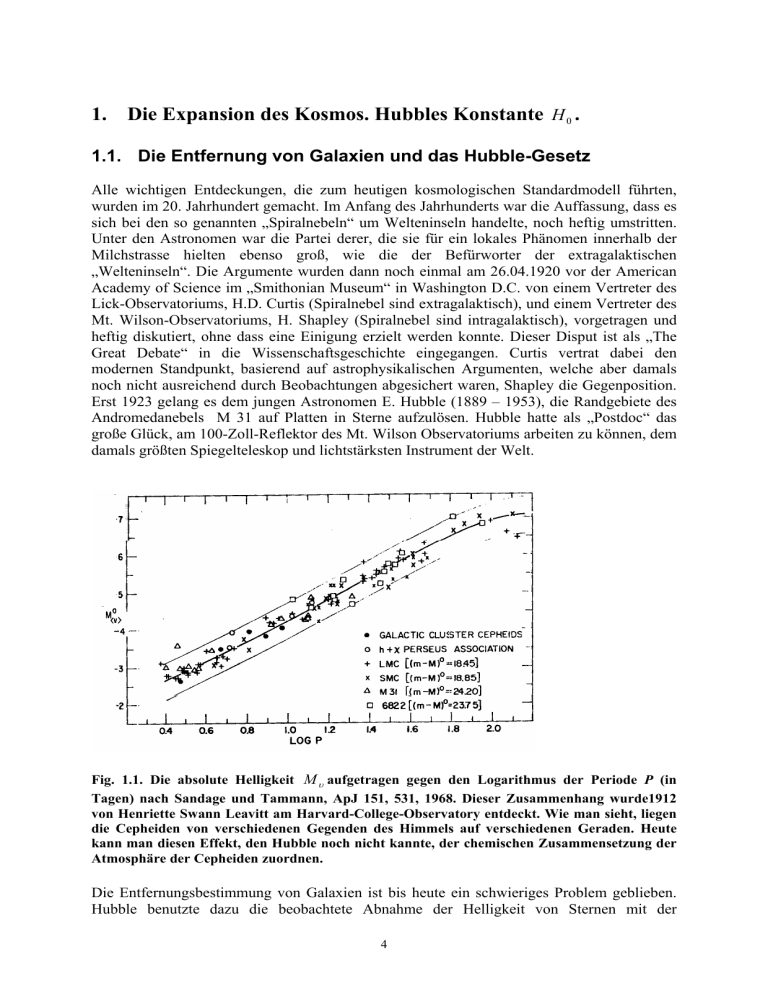
1. Die Expansion des Kosmos. Hubbles Konstante H 0 .
1.1. Die Entfernung von Galaxien und das Hubble-Gesetz
Alle wichtigen Entdeckungen, die zum heutigen kosmologischen Standardmodell führten,
wurden im 20. Jahrhundert gemacht. Im Anfang des Jahrhunderts war die Auffassung, dass es
sich bei den so genannten „Spiralnebeln“ um Welteninseln handelte, noch heftig umstritten.
Unter den Astronomen war die Partei derer, die sie für ein lokales Phänomen innerhalb der
Milchstrasse hielten ebenso groß, wie die der Befürworter der extragalaktischen
„Welteninseln“. Die Argumente wurden dann noch einmal am 26.04.1920 vor der American
Academy of Science im „Smithonian Museum“ in Washington D.C. von einem Vertreter des
Lick-Observatoriums, H.D. Curtis (Spiralnebel sind extragalaktisch), und einem Vertreter des
Mt. Wilson-Observatoriums, H. Shapley (Spiralnebel sind intragalaktisch), vorgetragen und
heftig diskutiert, ohne dass eine Einigung erzielt werden konnte. Dieser Disput ist als „The
Great Debate“ in die Wissenschaftsgeschichte eingegangen. Curtis vertrat dabei den
modernen Standpunkt, basierend auf astrophysikalischen Argumenten, welche aber damals
noch nicht ausreichend durch Beobachtungen abgesichert waren, Shapley die Gegenposition.
Erst 1923 gelang es dem jungen Astronomen E. Hubble (1889 – 1953), die Randgebiete des
Andromedanebels M 31 auf Platten in Sterne aufzulösen. Hubble hatte als „Postdoc“ das
große Glück, am 100-Zoll-Reflektor des Mt. Wilson Observatoriums arbeiten zu können, dem
damals größten Spiegelteleskop und lichtstärksten Instrument der Welt.
Fig. 1.1. Die absolute Helligkeit M υ aufgetragen gegen den Logarithmus der Periode P (in
Tagen) nach Sandage und Tammann, ApJ 151, 531, 1968. Dieser Zusammenhang wurde1912
von Henriette Swann Leavitt am Harvard-College-Observatory entdeckt. Wie man sieht, liegen
die Cepheiden von verschiedenen Gegenden des Himmels auf verschiedenen Geraden. Heute
kann man diesen Effekt, den Hubble noch nicht kannte, der chemischen Zusammensetzung der
Atmosphäre der Cepheiden zuordnen.
Die Entfernungsbestimmung von Galaxien ist bis heute ein schwieriges Problem geblieben.
Hubble benutzte dazu die beobachtete Abnahme der Helligkeit von Sternen mit der
4
Entfernung. Nötig sind dann aber Standard-Lichtquellen, deren Helligkeit bekannt ist. Hubble
verwendete dazu Cepheiden, Sterne deren Helligkeit sich periodisch ändert. Bei den
Cepheiden gibt es eine Beziehung zwischen Pulsationsdauer P und der absoluten Helligkeit
M υ , welche wurden. Die absolute Helligkeit eines Sterns ist die Helligkeit, die man in einer
Entfernung von 10 parsec beobachten würde. Die Entfernung 1 parsec (pc) = 3,086 ·1016 m.
Physikalisch ist M υ bis auf eine Konstante der Logarithmus der Strahlungsleistung (in Watt).
Die Cepheiden sind nach dem bekanntesten und hellsten Vertreter dieser Klasse, δ Cephei,
im Sternbild Cepheus benannt worden. Die Perioden-Helligkeits-Beziehung galaktischer
Cepheiden war von Henrietta S. Leavitt (1868 – 1921) aufgestellt worden. Sie hat die stolze
Zahl von etwa 2000 Cepheiden entdeckt. Dabei fand sie diesen Zusammenhang, den sie 1912
publizierte. Hat man aber die absolute Helligkeit eines Sterns und seine gemessene scheinbare
Helligkeit, dann ergibt sich daraus auch seine Entfernung (s. dazu Anhang A1).
Bereits Slipher hatte aus der Rotverschiebung von Spektrallinien
λ − λ0
=z
λ0
(1.1)
geschlossen, dass Spiralnebel sich z. T. mit extrem hohen Radialgeschwindigkeiten bewegen
müssten.
Fig. 1.2. Geschwindigkeiten von 1355 Galaxien aufgetragen gegen geschätzte Entfernungen. Die
Meßpunkte erfüllen in etwa Gl. 1.2. Die Streuung wird verursacht von Unsicherheiten der
Beobachtungen und von Eigenbewegungen der Galaxien, die nicht eliminiert wurden. Die
Skalierung der Entfernungen wurde vorgenommen unter der Annahme von
H 0 = 100 km ⋅ s −1 / Mpc
nach A. Liddle: An Introdurction to Modern Cosmology, J. Wiley
1998.
5
λ bedeutet hier die Wellenlänge einer Linie im Spektrum der beobachteten Galaxie, λ 0 die
im Labor gemessene Wellenlänge der entsprechenden Spektrallinie.
Fig.1.3. Edwin Hubble
1889 - 1953
Hubble fand Cepheiden auf den Aufnahmen der Nachbar-Galaxien und konnte damit die von
Slipher und Humason gemessenen Radialgeschwindigkeiten υ mit der von ihm selbst
bestimmten Entfernung r verknüpfen. Er fand aus den Beobachtungen das nach ihm benannte
Gesetz
υ = H 0r
(1.2)
welches er in dieser Form 1929 publizierte. Heute gilt Hubble allerdings nicht mehr als dessen
Entdecker sondern George Lemaitre, ein damals junger belgischer Astrophysiker und Priester.
Lemaitre hatte aus Einsteins Gleichungen unter dessen 1917 gemachten Voraussetzung von
Homogenität und Isotropie des Raumes ein expandierendes Weltmodel abgeleitet.
Homog. B-Feld:
v
B = (0,0, B z ) = konst.
Elektr. Feld einer
Punktladung:
r
1
E = ( E r ,0,0) ∝ 2
r
Kosmos
Homogenität
ja
Isotropie
nein
Nein
ja
Ja
ja
Tab. 1.1 : Zur Veranschaulichung von homogen und isotrop. Beides soll nach Einsteins
Annahme für den Kosmos erfüllt sein. Man nennt diese Voraussetzungen heute das
„kosmologische Prinzip“. Es ist für das frühe Universum außerordentlich gut erfüllt.
6
Er zeigte, dass dann (1.2) gelten müsse und versuchte diesen Schluss durch Daten aus
publizierten Beobachtungen zu unterstützen. Seine Publikation erschien 1927 in Belgien in
französischer Sprache. Erst eine englische Übersetzung von 1931 machten Lemaitres
kosmologische Überlegungen in der Fachwelt bekannt. Mehr dazu bei Nussbaumer s.
Literatur.
In der klassischen Form gilt das Gesetz für υ << c . Ersetzt man die so genannte
Fluchtgeschwindigkeit korrekt durch die Rotverschiebung, υ = cz , so verknüpft Lemaitres
Deutung die Rotverschiebung des Lichts mit der Expansion des Raumes, welche die Abstände
der Galaxien ebenso wie die Wellenlänge des Lichts um den Faktor (z + 1) vergrößert. Damit
können wir Gl. 1.2 wie folgt schreiben
z=
H0
r
c
(1.3)
In dieser Form ist das Hubblesche Gesetz auch für Objekte mit z > 0 richtig. Es ist hierbei
wichtig zu verstehen, dass die Rotverschiebung z nach Lemaitre keine Dopplerverschiebung
ist, sondern eine kosmologische Rotverschiebung, also ein Effekt der allgemeinen
Relativitätstheorie, bei welcher die Wellenlänge des Lichts mit der Expansion des Raumes
gedehnt wird..
Fig.1.4. George Lemaitre (1894 – 1966) und Albert Einstein (1879-1955).
Die Aufnahme entstand um 1933.
7
Fig.1.5. Darstellung des Hubble Gesetzes: Alle Galaxien scheinen sich von uns weg zu bewegen.
Aber ein entsprechendes Diagramm kann für einen beliebig gewählten Punkt im Raum
gezeichnet werden (s. Vektorschreibweise Gl. 1.4). Das ist eine Konsequenz von
Homogenität und Isotropie.
Bei naiver Betrachtung von Fig.1.5, in welcher das Hubblesche Gesetz durch
Geschwindigkeitsvektoren zu Objekten in verschiedenen Entfernungen veranschaulich wurde,
könnte man meinen, dass der irdische Beobachter eine bevorzugte Stellung einnimmt. Dafür
gibt es natürlich keinen ersichtlichen Grund. Das Bild ließe sich für einen beliebigen Ort im
Universum ebenso zeichnen. Diese Ortsunabhängigkeit (oder Translationsinvarianz) können
wir berücksichtigen, indem wir Gl. 1.2 als Vektorgleichung schreiben
r
r
υ = H 0r ,
(1.4)
Gl. (1.4) ist nun für jede beliebige Galaxie gültig. Ehe wir Gl. 1.4 interpretieren, wollen wir
noch einmal zu E. Hubble zurückkehren. Hubble fand für H0 einen Wert von etwa 500
km ⋅ s −1 / Mpc . Der heute akzeptierte Wert liegt bei 72 km ⋅ s −1 / Mpc . Wie war eine solche
Diskrepanz möglich? Ein Grund dafür ist: Hubble nutzte die Cepheiden als
Entfernungsindikatoren. Er konnte noch nicht wissen, dass die Helligkeits-PeriodenBeziehung auch von der chemischen Zusammensetzung der Sternatmosphäre abhängt. Der
Gehalt an schweren Elementen in der Sternmaterie steigt mit zunehmendem Alter der
betreffenden Region, in welcher der Veränderliche gefunden wird. Ein zweiter Grund:
Galaxien haben eine Eigenbewegung υ i entsprechend der Massen ihrer Umgebung. Sie kann
einige hundert km·s-1 betragen. Erst wenn die kosmologische Fluchtgeschwindigkeit sehr viel
größer ist, also υ >> υ i , lässt sich υ ausreichend genau bestimmen. Um den Wert der HubbleKonstanten wurde auf astronomischen Tagungen Jahrzehnte lang gerungen und gestritten,
was eben auch bedeutete, die systematischen Fehler zu finden, die sich in den Messungen der
verschiedenen Arbeitsgruppen verbargen. In Fig. 1.4 zeigen wir eine Graphik von einem der
Pioniere dieser Forschungen (G.A. Tammann: „The ups and downs of the Hubble constant“.
http://arxiv.org/abs/astro-ph/0512584)
8
Fig. 1.6. Die Bestimmung der Hubble-Konstanten von 1926 – 1962. Die Namen der Autoren
stehen bei den Werten. Aus G.A. Tammann: The Ups and Downs of the Hubble Constant.
Reviews of Modern Astronomy 19 (S. Röser Editor) Heidelberg 2006 oder
http://arxiv.org/abs/astro-ph/0512584
. Der von Hubble bestimmte Wert für H0 war gegenüber dem heutigen Werten um einen
Faktor 7 zu groß. Hubble hat ihn später nicht mehr berichtigt und sich auch an
kosmologischen Diskussionen nicht beteiligt. Die Bedeutung seiner Arbeiten ist unbestritten.
Dennoch ist es an der Zeit, seine Leistung von einer späteren Heldenverehrung zu trennen.
Als bester Wert für die Hubble-Konstante gilt heute aus der Kombination verschiedener
Bestimmungsmethoden
H 0 = 71 ± 8 km s −1 / Mpc
(1.5)
(1 Megaparsec (Mpc) = 3,057 ⋅10 22 m oder 3,2616 ⋅10 6 Lichtjahre). Man beachte, dass
1 / H 0 = t H eine Zeit ist, Hubble-Zeit genannt, ist, tH = 4,305·1017 s =13,65·109 Jahre =
4,30·1017 sek. und entsprechend ist c/H0 = 12,992·1022 km = 13,65·109 Lichtjahre = 4200 Mpc
die Länge der Strecke, welche das Licht in der Zeit tH zurücklegte, auch Hubble-Radius
genannt. Die Zeit, die seit dem Urknall vergangen ist, nennen wir t0 Sie steht für die JetztZeit t0 = 13,75·109 Jahre. Zu ihrer Berechnung benötigen wir ein Weltmodel, was wir im 2.
Kapitel behandeln werden. Dass sich t 0 ≅ t H ergibt, ist mehr ein zufälliges Zusammentreffen,
über das man gleichwohl spekulieren kann.
.
Obwohl die Cepheiden noch immer zu Entfernungsbestimmungen verwendet werden, sind die
bevorzugten Referenz-Lichtquellen für sehr große Entfernungen heute Supernovae vom Typ
Ia (abgekürzt SN Ia). Sie sind sehr viel heller und reichen deshalb in große Entfernungen.
Lichtstarke Teleskope mit großem Gesichtsfeld gestatten heute Supernovae in größerer
Anzahl und in weit entfernten Galaxien zu registrieren. Es handelt sich bei diesen
außerordentlich energiereichen Ereignissen um weiße Zwerge in engen Doppelsternsystemen.
Durch Massentransfer vom Begleitstern nimmt die Masse des weißen Zwergs allmählich zu.
Wird eine kritische Masse von ca. 1,44 Sonnenmassen (MO) überschritten, wird der weiße
Zwerg instabil. Es beginnt eine explosive Fusion von Kohlenstoff, welche den Stern völlig
zerstört. Da die kritische Masse, auch Chandrasekhar-Masse genannt, festliegt, wird bei jeder
9
SN Ia immer etwa die gleiche Energie frei. Im Maximum erreicht eine SN Ia in absoluten
bolometrischen Helligkeiten
M b = −19,6 ± 0,2
(1.6)
(s. hierzu den Anhang A1). Dazu kommen Korrekturen, die einerseits die Absorption durch
interstellaren Staub berücksichtigen, andererseits gewisse unterschiedliche Abläufe der SNExplosion, abhängig vom Gehalt schwerer Elemente. Diese Korrekturen werden gegenwärtig
ständig verfeinert.
Da Entfernungsbestimmungen für die moderne Astrophysik und Kosmologie essentiell sind,
werden möglichst verschiedene unabhängige Methoden dazu herangezogen. Dazu gehören
auch weiterhin die Cepheiden, die sich besonders für näher gelegene Galaxien eignen.
Fig. 1.7 Die beobachteten Helligkeiten von SN Ia sind aufgetragen gegen den Abstandsmodul
m − M = 5 log10 r / 10 pc (s. dazu A 1). Oben: unkorrigierte Werte. Unten: korrigiert auf
Grund der Abklingkurven der Supernovae. Nach P. Ruiz-Lapuente, Cosmology with
Supernovae. astro-ph /0304108.
(
)
Von anderen Methoden zur Eichung der Entfernungsskalen sei hier noch eine kurz erwähnt:
die Entfernungsbestimmung mittels einer Nova (bitte nicht mit einer Supernova
verwechseln!). Zu dieser leuchtkräftigen Erscheinung kommt es, wenn Materie, die sich auf
der Oberfläche eines weißen Zwergs angesammelt hat, durch Zündung einer Kernfusion
verpufft. Dabei werden die Fusionsprodukte mit hoher Ausbreitungsgeschwindigkeit
ausgeschleudert und bilden eine leuchtende sphärische Hülle. Wenn sich die
Ausbreitungsgeschwindigkeit υ h sowie die Winkelausdehnung α der Hülle, die sich im Laufe
10
weniger Jahre Δt sichtbar um Δα vergrößert, unabhängig messen lassen,kann daraus die
Entfernung r bestimm werden.
1.2. Kosmische Expansion.
Mit der Ableitung des Hubble-Gesetzes hatte George Lemaitre auch gleich die Interpretation
mitgeliefert. Nehmen wir einmal an, dass ungeachtet der durchaus inhomogenen
Massenverteilung im Kosmos, der Raum als isotrop und homogen angesehen werden kann.
r
Dann ist zu jeder Strecke r (t ) auch ein zeitabhängiger Skalenfaktor a (t ) anzugeben, der den
Expansionszustand des Raumes beschreibt, so dass gilt
r
r (t )
a (t )
=
r
r (t 0 ) a(t 0 )
(1.7)
r
Selbst wenn die Endpunkte der Strecke r gegenüber der Umgebung in Ruhe bleiben, ändert
sich der Abstand durch den (mit der Zeit anwachsenden) Skalenfaktor a (t ) . Wir können jetzt,
r
wenn der Koordinatenabstand r = konst. ist, Gl. 1.4 wie folgt schreiben
r
υ = a& (t )
r
r
r (t 0 ) a& (t ) r (t 0 )a (t )
=
a (t 0 ) a (t ) a (t 0 )
(1.8)
Wir definieren die Hubblefunktion durch
H (t ) =
a& (t )
a(t )
(1.9)
und erhalten so das Hubblesche Gesetz in einer etwas allgemeineren Form
r
r
υ = H (t )r (t )
(1.2a)
Man beachte, dass H0 in Gl. (1.2) die Hubblefunktion H(t) zur Jetztzeit t = t 0 ist.
Entsprechend schreiben wir den Skalenfaktor zur Jetztzeit a (t = t 0 ) = a 0 . Meist wird
a 0 = 1 gesetzt, was wir uns für später vorbehalten wollen.
Aber wie homogen ist der Kosmos wirklich? Man kann für die Massenverteilung eine
Hierarchisierung angeben, die Galaxien, Cluster von Galaxien, Supercluster (meist in Form
von Filamentstrukturen) enthält. Erst bei Entfernungen über 100 Mpc läßt sich von
Homogenität sprechen.
11
Fig.1.7. Wir können die kosmologische Rotverschiebung so verstehen, dass die Wellenlänge des
Lichts, die uns erreicht, seit der Zeit ihrer Emission mit der kosmischen Expansion gewachsen
ist (s. Gl. 1.10).
Wir kehren noch einmal zur kosmologischen Rotverschiebung der Spektrallinien z zurück.
Im Vorgriff auf eine spätere Ableitung verhält sich die beobachtete Wellenlänge des Licht wie
die entsprechenden Skalenfaktoren.
λ0 a (t 0 )
=
λ1 a (t1 )
(1.10)
λ0 ist die Wellenlänge eines Lichtsignals, welches der irdische Beobachter sieht und welches
zur Zeit t0 bei ihm ankommt. Als sich die Emission zur Zeit t1 < t 0 ereignete, hatte das Signal
im Ruhsystem des Emitters die Wellenlänge λ1 . Wenn wir die Rotverschiebung z als
z=
λ0 − λ1 a (t 0 )
=
−1 ,
a (t1 )
λ1
(1.11)
ansetzen erhalten wir mit a(t 0 ) = 1 und a (t1 ) = a schließlich
z +1 =
1
a
(1.12)
Es wurde in jüngster Zeit ein SN-Ereignis in einer Galaxie bei z = 9 beobachtet. Daraus lässt
sich die Entfernung r bestimmen. Wegen der endlichen Geschwindigkeit des Lichts ist es im
allgemeinen nicht möglich, die beiden Endpunkte einer Strecke im Kosmos „gleichzeitig“ zu
messen. Deshalb begegnen wir Schwierigkeiten, eine kosmische Entfernung eindeutig zu
definieren. Wir kommen darauf im nächsten Kapitel noch einmal zurück. Häufig wird aus z
auch die Zeit errechnet, welche seit der Lichtemission vergangen ist („look back time“). Das
ist allerdings erst dann möglich, wenn man ein bestimmtes Weltmodell zugrunde legt, was wir
im 2. und 3. Kapitel tun werden.
1.3. Wie alt ist der Kosmos?
12
Aus Gl. 1.1. und 1.2 sieht man, dass die Hubblekonstante H0 die Dimension einer reziproken
Zeit t0 hat. Da wir z.Zt. die Hubble-Konstante nur auf etwa 4 % genau kennen, geben wir die
−1
Hubble-Zeit tH für H 0 = 100h km ⋅ s / Mpc . Danach ist
t H = H 0−1 =
9.79 ⋅ 10 9 Jahre
= 13,65 ⋅ 10 9 Jahre = 4,34 ⋅ 1017 Sek
h
(1.10)
H0
ist. Mit dem heutigen Wert von H0 ist h = 0,72 . Welche Rolle t0
100km ⋅ s −1 / Mpc
spielt, werden wir erst bei der Behandlung der Weltmodelle erkennen. Wir können aber jetzt
schon t0 als Obergrenze des kosmischen Alters ansehen. Erste Sterne und erste Galaxien sind
heute 13,2 ·109 Jahre alt. Wenn das Universum selbst 13,7·109 Jahre alt ist, sind sie etwa 500
Millionen Jahre nach dem Beginn entstanden.
wobei h =
1.4. Zusammenfassung
r
Das Hubble-Gesetz verknüpft die „Fluchtgeschwindigkeit“ υ der Galaxien linear mit ihrer
r
Entfernung r . Der Proportionalitätsfaktor heißt Hubble-Konstante H0 und ist ein wichtiger
Parameter der Kosmologie. Heute lässt sich H 0 = 72 km·s-1/Mps mit einer Genauigkeit von
etwa 4% angeben. Da die Rotverschiebung kein Dopplereffekt ist sondern durch die
Expansion des Raumes zustande kommt, gibt man anstatt υ heute die Rotverschiebung der
Spektrallinien z an. Zur Bestimmung von H0 bedient man sich der Ereignisse von Supernovae
Ia. Die Expansion des Raumes wird durch einen Skalenfaktor a (t ) in allen extragalaktischen
Entfernungen berücksichtigt. Erste Sterne sind bereits 500 Millionen Jahre nach dem Urknall
entstanden. 1 / H 0 = t H hat die Dimension Zeit, t H = 4,305 ⋅ 1017 sec und entsprechend ist
c / H 0 = 12,992 ⋅ 10 22 km = 13,5 ⋅ 1010 Lichtjahre die Länge der Strecke, welche das Licht in der
Zeit t H zurücklegt.
1.5. Literatur
J. Silk : Die Geschichte des Kosmos. Vom Urknall bis zum Universum der Zukunft.
Spektrum Akademischer Verlag 1996, 1999 als Taschenbuch
Simon Singh : Big Bang. Der Ursprung des Kosmos und die Erfindung der modernen
Naturwissenschaft. DTV 2007
A. Liddle: An Introduction to Modern Cosmology, J. Wiley 2003.
G.A. Tammann: The Ups and Downs of the Hubble constant. In Reviews of Modern
Astronomy 19 (S. Röser Editor) Heidelberg 2006
C P. Ruiz-Lapuente : Cosmology with Supernovae. http://arxiv.org/astro-ph /0304108
13
D.J. Mortlock: A luminous quasar at a redshift of z = 7,085. Nature, published online 30 June
2011.
Anna Frebel, McDonald Observatory Texas, USA: A galactic fossil. Star is found 13.2 billion
years old. http://www.eso.org/public/news/eso0723/
Harry Nussbaumer: Achzig Jahre expandierende Universum. Sterne u. Weltraum 6/2007 S. 37-44
1.6. Aufgaben
1.6.1. Die mittlere Radialgeschwindigkeit, die man in den Eigenbewegungen der
Galaxien findet, ist ca. 250 km/s. Wie groß muss die Hubblesche
Fluchtgeschwindigkeit wenigstens sein, damit die Eigenbewegung nur 1% der
kosmologischen Bewegung ausmacht? Welcher Rotverschiebung z entspricht das
(ohne relativistische Rechnung)?
1.6.2. Bei einer sehr fernen Galaxie liegt die Grenze der Lyman-Serie ( n = 1 → n = ∞ )
bei 400 nm. Wie groß ist die Rotverschiebung z? Wo würde die Hα-Linie
( n = 2 → n = 3 ), die üblicherweise das Spektrum heißer Sterne beherrscht,
liegen? Könnte man sie mit terrestrischen Teleskopen beobachten?
1.6.3. Die Hubble-Funktion ist durch die Gleichung
a& (t )
= H (t )
a(t )
gegeben. Mache Angaben über H (t ) , in dem du folgenden Ansätze für
a (t ) ausprobierst:
2⎛ t
a(t ) = ⎜⎜
3 ⎝ tH
⎞
⎟⎟
⎠
2
3
(Hier ist t H = H 0−1 die Hubble-Zeit) und
a (t ) = A exp λ t
1.7.
Kurzvorträge (15 min.)
SN Ia
Cepheiden
Projekt „Hipparchos“
14