Grundlagen der empirischen Sozialforschung

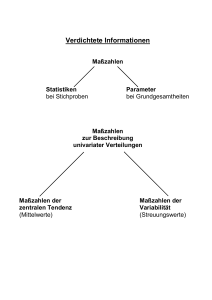
Grundlagen der empirischen Sozialforschung
Sitzung 10 - Datenanalyseverfahren
Jan Finsel
Lehrstuhl für empirische Sozialforschung
Prof. Dr. Petra Stein
22. Dezember 2008
1 / 21
Online-Materialien
I
Die Materialien zur Vorlesung finden Sie auf der Homepage
http://www.uni-due.de/soziologie/stein_lehre.php
I
Die ganze Vorlesung ist dort auch als Stream verfügbar
I
Es gibt eine Übung von Dawid Bekalarczyk um 14 bis 16 Uhr
am Montag in Raum S-E 005 hier in Essen
I
Im Sekretariat von Frau Werner in Raum R12 R06 A30
können CDs bzw. DVDs erstanden werden
I
Meine Materialien finden Sie auf meiner Seite
http://www.uni-due.de/soziologie/finsel.php
I
Mail: [email protected]
2 / 21
Der Plan für heute I
1
Die Hausaufgabe
2
Struktur des Vorlesungsblockes Datenanalyseverfahren
Vorlesungsblock Datenanalyseverfahren - sechs Sitzungen
3
Aufgabe
Die Bedeutung von Messniveaus für Lage-, Streuungsmaße,
Grafiken und für bivariate Zusammenhangsmaße
Maßzahlen zur Beschreibung univariater Verteilungen Verdichtete Informationen
Verdichtete Informationen
4
Arithmetisches Mittel
Berechnung von x
Median
Beispiel: Median
Bestimmung des Medians
Modus (h)
5
Maßzahlen zur Beschreibung univariater Verteilungen Streuungsmaße
Grafik zur Veranschaulichung
3 / 21
Der Plan für heute II
Streuungsmaße: Range und Quartilsabstand
Grafik zur Veranschaulichung
Streuungsmaße: Varianz und Standardabweichung
Berechnung von s 2 und s
6
Selberrechnen
Aufgabe: Berechnung von
Lösung: Berechnung von
4 / 21
Vorlesungsblock Datenanalyse - sechs Sitzungen
Ablauf
1. Einführung, Univariate Verteilungen: Tabellarische Darstellung
2. Univariate Verteilungen: Graphische Darstellung
3. Verdichtete Informationen: Maßzahlen zur Beschreibung
univariater Verteilungen
4. Bivariate Analyse der Beziehung zwischen nominalen Variablen
5. Bivariate Analyse der Beziehung zwischen ordinalen Variablen
6. Bivariate Analyse der Beziehung zwischen metrischen
Variablen
Abweichung vom Online-Material
Die Regressionsanalyse fällt raus
5 / 21
Aufgabe
Anhand des Fragebogens jeweils zwei Variablen für
jedes Messniveau finden und die Entscheidung
begründen.
Die Frägebögen finden sich ab Seite 267 in:
Wolfgang Melzer & Wilfried Schubarth 2006: Gewalt als soziales
Problem an Schulen Untersuchungsergebnisse und
Präventionsstrategien. Ein eBook im Open Access. Verlag Barbara
Budrich, Opladen
6 / 21
Die Bedeutung von Messniveaus für Lage-, Streuungsmaße,
Grafiken und für bivariate Zusammenhangsmaße
Skalenniveau
Lagemaße
Nominal
Ordinal
Metrisch
häufigster Wert
= Modus (h)
Median
(xe)
arithmetisches
Mittel (x )
Quartile,
(mittlerer)
Quartilsabstand
(QA)
Varianz (s 2 ),
Standardabweichung (s)
Streuungsmaße
Grafiken
Balken-, Kreis(Torten-)diagramm
Balken-, Kreis(Torten-)diagramm,
Box-plot (boxand-whisker-plot)
Histogramm,
Polygonzug,
box-andwhisker-plot
(Bivariate)
Zusammenhangsmaße
χ2 basierte Maßzahlen:
Phi, Cramers V,
Kontingenzkoeffizient C
Rangkorrelationskoeffizient Spearmans rho rs
Pearsons r
Produkt-MomentKorrelationskoeffizient
7 / 21
Maßzahlen zur Beschreibung univariater Verteilungen
I
Maßzahlen der Maßzahlen der zentralen Tendenz
(Mittelwerte)
I
Variabilität (Streuungswerte)
8 / 21
Verdichtete Informationen
Lagemaße (Maße der zentralen Tendenz)
Eine Maßzahl der zentralen Tendenz (im Benninghaus: Mittelwert)
ist der Kennwert, der die gesamte Verteilung am besten
repräsentiert
I
Arithmetisches Mittel
I
Median
I
Modus
9 / 21
Arithmetisches Mittel
Lagemaße (Maße der zentralen Tendenz)
Arithmetisches Mittel x (liest sich x quer)
I
Erfordert metrisches Messniveau
I
x=
I
oder einfacher zu rechnen
I
x=
x1 +x2 +...+xN
N
Σfi ·xi
N
10 / 21
Berechnung von x
xi
10
11
12
13
14
15
16
17
18
19
28
Gesamt
x=
fi · xi
Häufigkeit
fi
2
550
454
599
604
711
400
84
4
1
1
Σfi ·xi
N
3410
=
46373
3410
20
6050
5448
7787
8456
10665
6400
1428
72
19
28
P
fi · xi = 46373
= 13, 6
11 / 21
Median
Lagemaße (Maße der zentralen Tendenz)
Median xe
I
Erfordert metrisches Messniveau
I
xe (liest sich x Schlange)
I
Der Median ist der Wert, welcher eine geordnete Reihe in zwei
Hälften spaltet.
I
50 % der Fälle liegen über bzw. unter dem Median.
I
Vorteil: Im Gegensatz zum arithmetischen Mittel wird der
Median nicht von Extremwerten beeinflusst.
12 / 21
Beispiel: Anzahl der Kühe pro Bauer in einem Dorf mit 5
Bauern
Lagemaße (Maße der zentralen Tendenz)
0 0 0 0 200
⇒ xe = 0 und x = 40
13 / 21
Berechnung von xe
Häufigkeitstabelle des Merkmales Alter
xi
Häufigkeit
fi
Kumulierte
Prozente
P
fi
N
10
11
12
13
14
15
16
17
18
19
28
2
550
454
599
604
711
400
84
4
1
1
N = 3410
· 100
0.1
16.2
29.5
47.1
64.8
85.6
97.4
99.8
99.9
100.0
100.0
⇐ xe = 14
14 / 21
Modus (h)
Lagemaße (Maße der zentralen Tendenz)
Der Modus ist der Wert, der in einer Verteilung am häufigsten
vorkommt (dichtester Wert)
Beispiel: h = 7
5 6 6 7 7 7 8 8 9 10
Beispiel: h = 7,5 aufgrund von benachbarten
Häufigkeitsmaxima
5 6 6 7 7 7 8 8 8 9 10
15 / 21
Abbildung: Zwei Verteilungen mit gleicher
x = h = 100 ),
zentraler Tendenz ( x = ~
aber ungleicher Streuung
x=~
x = h = 100
70
80
100
110
130
Streuungsmaße: Range und Quartilsabstand
Die Streuungswerte haben die Aufgabe, die Variabilität des
gemessenen Merkmals zu beschreiben
Der Range
I
Der Range ist definiert als die Differenz zwischen dem größten
und dem kleinsten Messwert einer Verteilung
I
Der Range ist das einfachste Streungsmaß
I
R = xmax − xmin
I
Nachteil: Wird sehr stark durch Extremwerte beeinflusst
Der Quartilsabstand und der mittlere Quartilsabstand
Quartilsabstand = Q3 - Q1
16 / 21
STREUUNGSWERTE
(VARIABILITÄTSMAßE)
Die Streuungswerte haben die Aufgabe, die Variabilität des
gemessenen Merkmals zu beschreiben.
1. Der Range
Der Range ist definiert als die Differenz zwischen dem größten
und dem kleinsten Messwert einer Verteilung.
R = xmax – xmin
2. Der Quartilsabstand und der mittlere
Quartilsabstand
Abbildung: Illustration der Quartile und des Quartilsabstandes
50 %
1
4
1
4
Q1
1
4
Q2 = ~
x
Quartilsabstand
Quartilsabstand = Q3 - Q1
1
4
Q3
Streuungsmaße s 2 und s
Streuungsmaße
I
Lagemaße geben typische Werte einer Verteilung an
I
Streuungsmaße geben an wie stark vom typischen Wert
arithmetisches Mittel abgewichen wird
Varianz s 2
P
(xi −x )2
N
P
fi ·(xi −x )2
N
I
Varianz = s 2 =
I
Die Varianz steht für den Gesamtumfang der Abweichungen
vom Mittelwert
=
17 / 21
Streuungsmaße s 2 und s
Standardabweichung s
rP
(xi −x )2
N
I
Standardabweichung = s =
I
Die Standardabweichung bezeichnet die durchschnittliche
Abweichung in der originären Maßeinheit
I
Standardabweichung und Varianz erfordern metrisches
Messniveau
18 / 21
Berechnung von s und s 2
Häufigkeit
fi
xi − x
(xi − x )2
fi · (xi − x )2
10
2
-3.6
12.96
25.92
11
12
13
14
15
16
17
18
19
28
550
454
599
604
711
400
84
4
1
1
-2.6
-1.6
-0.6
0.4
1.4
2.4
3.4
4.4
5.4
14.4
6.76
2.56
0.36
0.16
1.96
5.76
11.56
19.36
29.16
207.36
3718
1162.24
215.64
96.64
1393.56
2304
971.04
77.44
29.16
207.36
xi
N = 3410
P
s2 =
P
fi ·(xi −x )2
N
x = 13, 6
s2 =
10201
3410
s 2 = 2, 99
√
s=
s 2 = 1, 73
= 10201
19 / 21
Aufgabe: Berechnung von
x , xe , s und s 2
P
xi
10
11
12
13
14
15
16
17
18
Häufigkeit
fi
fi · xi
xi − x
fi %
(xi − x )2
fi · (xi − x )2
1
323
614
389
681
499
551
38
2
N = 3098
P
P
=
x =;
s2 =
=
xe =
Σfi ·(xi −x )2
N
=;
s=
20 / 21
Lösung: Berechnung von x , Pxe , s und s 2
xi
10
11
12
13
14
15
16
17
18
Häufigkeit
fi
fi × xi
fi %
xi − x
(xi − x )2
fi × (xi − x )2
1
323
614
389
681
499
551
38
2
10
3553
7368
5057
9534
7485
8816
646
36
0.03
10.46
30.28
42.83
64.82
80.92
98.71
99.94
100.00
-3.72
-2.72
-1.72
-0.72
0.28
1.28
2.28
3.28
4.28
13.84
7.40
2.96
0.52
0.08
1.64
5.20
10.76
18.32
13.84
2389.68
1816.46
201.66
53.39
817.56
2864.32
408.82
36.64
N = 3098
P
P
= 42505
x=
s2 =
42505
3098
= 13, 72;
Σfi ×(xi −x )2
N
=
8602.37
3098
= 8602.37
xe = 14
= 2, 78;
s = 1, 67
21 / 21