Blatt 7

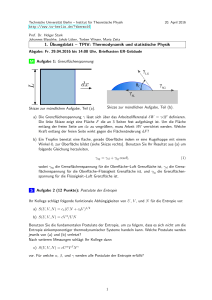
Theoretische Physik
Thermodynamik und statistische Physik (T4)
Prof. Dr. U. Schollwöck
10. Juni 2013
Blatt 7
Sommersemester 2013
Aufgabe 19: Grenzflächenspannung
Thermodynamische Eigenschaften von Grenzflächen zwischen zwei Phasen werden durch
die sogenannte Grenzflächenspannung σ beschrieben. Diese ist durch die Arbeit, welche
benötigt wird, um die Grenzfläche um dA zu vergrößern, definiert, d.h. dW = σdA.
a) Zeigen Sie, dass der Druck innerhalb eines sphärischen Wassertropfens mit Radius
R um 2σ/R größer ist als der äußere Druck, indem Sie die Arbeit betrachten, welche gegen die Grenzflächenspannung bei einer infinitesimalen Änderung des Radius
verrichtet wird.
b) Ein Wassertropfen kondensiert auf einer festen Oberfläche. Dabei spielen drei verschiedene Grenzflächenspannungen eine Rolle: σlw , σow , σol . Hierbei stehen l, o, w
respektive für Luft, die feste Oberfäche und Wasser. Berechnen Sie den Kontaktwinkel Θ zwischen der Oberfläche und dem Wassertropfen und finden Sie die Bedingung
für das Auftreten eines Wasserfilms.
c) Im Grenzfall großer Systeme kann man Oberflächeneffekte meist vernachlässigen.
Bei kleineren Systemen jedoch können diese Effekte wichtig werden. Schätzen Sie
die typische Längenskala, welche große“ von kleinen“ Systemen in den folgenden
”
”
physikalischen Situationen trennt, ab. (Die Grenzflächenspannung von Wasser in Luft
bei Raumtemperatur beträgt σlw ≈ 7 × 10−2 N m−1 ).
1. Ein kleiner Wassertropfen befindet sich auf einer Oberfläche ohne Benetzung. Die
Grenzflächenspannung verhindert, dass dieser wesentlich durch die Gravitationskraft verformt wird.
2. Ein Geltropfen befindet sich in gesättigtem Wasserdampf. Der durch die Grenzflächenpannung verursachte Druckunterschied innherhalb und außerhalb des Geltropfens verhindert dessen Anwachsen. (Der osmotische Druck beträgt typischerweise 1 atm).
Abbildung 1: Wassertropfen auf fester Oberfläche mit Kontaktwinkel Θ.
1
Aufgabe 20: Grenzflächenaktive Substanzen
Grenzflächenaktive Moleküle, wie sie zum Beispiel in Spülmitteln oder Haarwaschmitteln
vorkommen, sammeln sich an der Grenzfläche zwischen Luft und Flüssigkeit, anstatt
sich in der Flüssigkeit zu lösen. Dadurch wird die Grenzflächenspannung reduziert. Dies
kann beispielsweise demonstriert werden, indem man ein Haar auf einer Wasseroberfläche
schwimmen lässt und dann ein wenig Spülmittel hinzugibt, wodurch das Haar im Wasser
versinkt.
a) Die Luft-Wasser Grenzflächenspannung σlw wird in etwa um N kB T /A reduziert, wenn
dem Wasser N grenzflächenaktive Moleküle hinzugefügt werden und A die Grenzfläche ist. Geben Sie hierfür eine qualitative Erklärung.
b) Geben Sie einen Wassertropfen auf eine glatte Oberfläche und beochbachten Sie, was
passiert, wenn Sie dem Tropfen eine kleine Menge Spülmittel hinzugeben. Wie ändert
sich der Kontaktwinkel? Erklären Sie das Beobachtete.
c) Genauere Versuche zeigen, dass bei höheren Konzentrationen von grenzflächenaktiven
Molekülen
2
2a N
N kB T
∂T A − Nb
∂σ −
=
und
=−
2
∂A T
(A − N b)
A A
∂σ A
N kB
mit Konstanten a und b gelten. Bestimmen Sie den Ausdruck für σ(A, T ) und erklären
Sie qualitativ den Ursprung der durch a und b beschriebenen Korrekturen.
δQ δQ ∂E ∂E d) Finden
Sie
einen
Ausdruck
für
C
−C
=
−
als
Funktion
von
=
,
σ
A
δT
δT
∂A
∂A
σ
A
T
σ
∂σ ∂T σ, ∂A T und ∂σ A .
Aufgabe 21: Zustandsgleichungen
Die Zustandsgleichung schränkt die Form der inneren Energie ein. Dies soll in den folgenden Beispielen demonstriert werden.
a) Zeigen Sie beginnend von dE = T dS−P dV , dass die Zustandsgleichung P V = N kB T
impliziert, dass E nur von T abhängen kann.
b) Welche ist die allgemeinste Zustandsgleichung, die konsistent mit der Annahme ist,
dass die innere Energie nur von der Temperatur abhängt?
2
c) Die Zustandsgleichung des van der Waals Gases lautet P −a( N
)
· (V − N b) =
V
eine Funktion ausN kB T . Zeigen Sie, dass für das van der Waals Gas Cv = ∂E
∂T V
schließlich der Temperatur ist.
2