Didaktik der Arithmetik

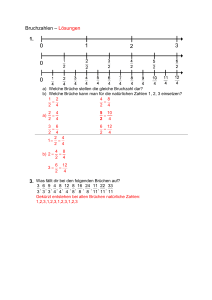
Dr. U. Baltes
WS 2010/11
Didaktik der Arithmetik
Übung 12: Bruchrechnen II
Abgabe: 11.01.11 vor der Vorlesung
Schriftliche Hausaufgabe
In seinem Klassiker „Didaktik der Bruchrechnung“ (zuletzt Heidelberg/Berlin: Spektrum
2003) unterscheidet F. Padberg (in etwas anderer Reihenfolge) vier Konzepte zur Behandlung
der Bruchrechnung:
1. das Größenkonzept 2. das Operatorkonzept
3. das Äquivalenzklassenkonzept 4. das Gleichungskonzept
12.1 Nach verbreiteter Auffassung werden in der „Förderstufe“ (= Orientierungsstufe in
Hessen) nur die beiden ersten Konzepte verwendet, und zwar in der angegebenen
Reihenfolge. Warum nur diese, warum in dieser Reihenfolge?
12.2 Das Gleichungskonzept wird gemeinhin dem Mathematiker und Didaktiker Hans
Freudenthal (1905-1990) zugeschrieben. Nach dessen Ansicht, die er höflicherweise
seinem Schüler van Hiele zuschrieb, ist „die dem Bruchrechnen zugrunde liegende Idee
und die zu ihr führende Motivation algebraisch… So sollte das Bruchrechnen, soweit es
unanschaulich ist, dann auch motiviert werden – das gebietet schon die Ehrlichkeit – man
verlangt die unbeschränkte Ausführbarkeit der vier Operationen. Das ist eine abstrakte, von
der Praxis kaum beeinflusste Motivation, und mit ihr befindet man sich mitten in der
Algebra… Es werden heute sehr viel Anstrengungen gemacht, das Bruchrechnen im
Rahmen des elementaren Rechnens zu verbessern… Wenn sie didaktisch gut sind, sind sie
besonders gefährlich, weil sie die wirkliche Lösung hinausschieben – ein endloser Aufschub.
Die wirkliche heißt für mich: von der Algebra her.“ (H. Freudenthal: Math. Als päd. Aufgabe,
Band 1. Stuttgart: Klett 1973, S. 248.)
Hans Freudenthal
Pierre van Hiele
Welche „Motivationen“ gibt es für das „gemeine“ Bruchrechnen außer der algebraischen
noch, und warum ist Algebra ohne „gemeine“ Bruchrechnung schwierig?
12.3 (Teilungen eines Quadrats)
Aus einem großen Quadrat soll durch Faltung ein kleineres Quadrat hergestellt werden,
1
dessen Flächeninhalt
des Flächeninhalts des ursprünglichen Quadrats ausmacht.
5
Stellen Sie das Falten des Quadrats auch durch eine Zeichnung dar.
12.4 (Stammbrüche)
Geben Sie alle Möglichkeiten für x,y ∈ N an, so dass
1
1
1
+
= . Begründung!
x
y
4
12.5 (Stichworte):
Nach einem Bonmot haben Brüche viele Gesichter. Ein Bruch wie 3/7 kann als Teil eines
oder mehrerer Ganzer begriffen werden, als Operator, als Maßzahl, als Verhältnis, als
Quotient, als Lösung von Gleichungen, als Marke auf einer Skala. Was bedeuten diese
Aspekte
im Einzelnen, und was bedeuten dabei jeweils die vier Grundrechenarten?
Mündliche Hausaufgabe
12.6 (Zur Wiederholung)
a) Geben Sie vier Aspekte an, in denen sich Bruchzahlen von natürlichen Zahlen
unterscheiden.
b) Geben Sie fünf verschiedene Möglichkeiten an, eine Bruchzahl zu bestimmen, die
zwischen zwei gegeben verschiedenen Bruchzahlen liegt.
c) Auf welche Weise sollen Schülerinnen und Schüler am Ende der Jahrgangsstufe 6
Bruchteile deuten können? (vgl. Kernlehrpläne / Kompetenzerwartungen)
12.7 (Stammbrüche)
a) Berechnen Sie und setzen Sie fort:
1 1
1 1
1
1 1
1
1
1
,
+ ,
+
+ ,
+
+
+
,…
2 2
4 2
4
8 2
4
8
16
Was ergibt sich, wenn man immer mehr solcher Brüche addiert?
Belegen Sie Ihre Entdeckung durch eine instruktive Zeichnung.
b) In dem mehr als 3500 Jahre alten ägyptischen Rechenbuch des Ahmes wird bereits
mit Brüchen gerechnet. Allerdings kommen nur Stammbrüche – Brüche mit dem
Zähler 1 – vor;
andere Brüche werden als Summen von Stammbrüchen geschrieben.
Drücken Sie die folgenden Brüche als Summen verschiedener Stammbrüche aus:
7
5
19
,
,
.
12
9
20
12.8
Suchen Sie aus Schulbüchern für die 5.-7. Klasse möglichst viele wirklichkeitsnahe
Anwendungen, in denen die „gemeinen“ Bruchrechenarten wirklich gebraucht werden.