Elektrizitätslehre 3

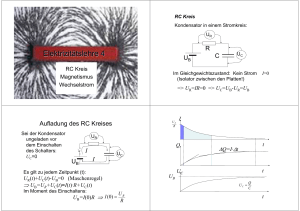
Elektrizitätslehre 3
Elektrischer Strom
Strom = Bewegung der Ladungen
Strom im Vakuum
Strom im Gas
Strom in Flüssigkeit (Lösung)
Strom im Festkörper
Strom im Vakuum:
Freie Ladungsträger werden im elektrischen
Feld beschleunigt :
E
q
v
F
m
F
a=
m
U
W = Uq = 12 mv 2
Elektrische Energie => mechanische Energie
Strom im Gas
Ladungsträger: Ionen und Elektronen
Gasatome
q
F
Strom in Lösungen
Elektrolyt: Ionen + und –
z.B. Na+ Cl- ;Ca2+ CO32-
E
Wassermoleküle
v
E
m
Freier Weg
(Beschleunigung)
T~ durchschnittliche kin. E
Elastischer
Zusammenstoß
Abbremsung,Energieübergabe
=> Wärme, Licht
Strom in Metalle
Metall: Feste Atomkerne mit
geschlossenen Elektronenhüllen
Die Elektronen der äußere Hüllen
bewegen sich frei. (Sie sind
„kollektive“ Elektronen)
Al Atom
Al Metall
3
8
K
K
K
2
K
L
L
L
L
13=Z M
Elektrische Energie => Wärme
+chemische Energie
Strom in Metalle:
Wanderung der Elektronen.
L
K
L
K
L
K
U
Zusammenstoß mit der Atome =>
=> Wärme
Elektrische Energie => Wärmeenergie
Bemerkung: Wärmebewegung (km/s)
Strombewegung (mm/s)
(Driftgeschwindigkeit)
Analogie: Warenhaus
Elektrische Stromstärke
Durch einen
Leiterquerschnitt
während Δt Zeit
durchgeflossene
Ladung
ΔQ
I=
Δt
Einheit: Ampere (A)
1A = 1C/1s
Konventionelle Stromrichtung: Bewegungsrichtung der positive Ladungen.
Wirkungen des Stromes
Wärmewirkung
Chemische Wirkung
Magnetische Wirkung
Strom in Metalle:
Wanderung der Elektronen.
L
(Biologische Wirkung)
(Lichtwirkung)
K
L
K
L
K
U
Zusammenstoß mit der Atome =>
=> Wärme
Elektrische Energie => Wärmeenergie
Bei Metallen gilt ein Zusammenhang
zwischen der Spannung und Stromstärke:
Spannung und Stromstärke
I ~ U
d.h. U/I ist konstant. Diese Konstante wird
als Widerstand bezeichnet:
R=
U
I
Einheit : Ohm Ω =
V
A
Ohmsches Gesetz
Einige spezifische Widerstandswerte:
Widerstand eines Leiters
I ~ v ~ E = U/l
I~Q~A
I
A
l
A ⎫
U
l ⎪R~ l ⇒R=ρ l
U ⎬
A
A
⎪
I=
R ⎭
I~
Spezifischer Widerstand
Ωm; Ωmm2/m
Stoff
ρ (Ωmm2/m)
Silber
Kupfer
Gold
Aluminium
Eisen
Wolfram
Konstantan
0,016
0,017
0,023
0,028
0,1
0,05
0,5
ρ (Ωmm2/m)
Stoff
Kohlenstoff
≈35
Dest. Wasser
1010
Transformatorenöl 1015-1016
Porzellan
1018
Quarzglass
5·1022
Spezifische Leitfächigkeit: σ =
1
ρ
Widerstand als physikalische Größe
und Schaltelement
Parallelschaltung von Widerstände
U1
R1 I1
R=
U
I
[ Ω]
R2
I U
I2
I
U2
U
U U
U U
= 1+ 2 = +
R p R1 R2 R1 R2
U1=U2=U
I=I1+I2
Reihenschaltung von Widerstände
U1
I1 R
1
I2
Rp
1
1
1
= +
R p R1 R2
Parallel- und Reihenschaltung von Widerstände
R1 A 1
R
p
U2
I U
R2
Rr
I1=I2=I
U=U1+U2
IRr = I1R1 + I 2 R2 = IR1 + IR2
Rr = R1 + R2
R2
A2
R ~ 1/A A ~ 1/R
l1
l2
R1
R2
R~ l
1
1
1
= +
R p R1 R2
A=A1+A2
l =l1+l2
Rr
Rr = R1 + R2
Einfachster Stromkreis
Elektrischer Stromkreis
z.B.: Leselampe:
Elektrische Schaltelemente
Baterie
U
Widerstand
Schalter
U
Spannungsquelle
Lampe
Kondensator
Strom- und Spannungsmessung
V
I
Spannungsmessgerät
in Parallelschaltung
Ideale Spannungsquelle:
Spannung ist unabhängig der
Stromstärke
Reelle Spannungsquelle: Innerer Widerstand
U0
Uk
I
A
Strommessgerät in
Reihenschaltung
I
Uk=U0-IRi
U0: Leerlaufspannung
Elektromotorische Kraft
Uk: Klemmenspannung der Spannungsquelle
U0 ≥ Uk ≥ 0
Joulesche Wärme und Elektrische Leistung
I
L
K
L
K
L
K
U
Elektronenbewegung:
Beschleunigung, Zusammenstoß
Energieaufnahme
Um Q Ladung gegen U Spannung zu
transportieren braucht man W=QU
Energie.
Wenn sich Q Ladung durch das
elektrische Feld bewegt, gibt das Feld
W=UQ=UIt Energie ab.
Diese Energie wird in Wärme
umgewandelt. (Joul‘sche Wärme)
W=U I t
Energieabgabe
Kirchoffsche Gesetze
Die Elektrische Leistung:
1. Kirchoffsches Gesetz: Knotenregel
W UIt
P=
=
= UI
t
t
Einheit: Watt
I1>0
1W=1V A
Zum Vergleich:
I3>0
20-40 W
5-100 mW
50-100 W
1-2 kW
~100 W
I1+I2+I3+I4=0
I2<0
I4<0
RC Kreis
2. Kirchoffsches Gesetz: Maschenregel
Summe der Spannungen in einer Masche ist =0
Kondensator in einem Stromkreis:
UR
UB1
U1 R 1
-UB1+U3+U2+UB2+U1=0
R
UB
R 3 U3
I
R2
U2
UB2
UC
Im Gleichgewichtszustand: Kein Strom
(Isolator zwischen den Platten!)
-UB1+IR3+IR2+UB2+IR1=0
Aufladung des RC Kreises
Sei der Kondensator
ungeladen vor
dem Einschalten
des Schalters:
UC=0
C
I=0
=> UR=IR=0 => UC=UB-UR=UB
UB
R
I
UR
Q
I
UB
I
UC
Es gilt zu jedem Zeitpunkt (t):
UB
UR(t)+UC(t)-UB=0 (Maschenregel)
⇒ UB=UR+UC(t)=I(t)·R+UC(t)
Im Moment des Einschaltens:
UB=I(0)R ⇒ I (0) =
t
ΔQ=I·Δt
t
UC
UC =
UB
R
Q
C
t
Entladung des RC Kreises
Die Stromstärke annähert Null asymptotisch.
UR=IR => UR annähert Null asymptotisch.
UC annähert UB asymptotisch.
t
−
⎛
τ
⎜
U C = U B ⎜1 − e
⎝
U R = U Be
−
Sei der Kondensator vor dem Einschalten des
Schalters aufgeladen:
UR
U (0)=U
C
0
Maschenregel:
⎞
⎟
⎟
⎠
τ = RC
I (t ) =
t
τ
I
UR(t)-UC(t)=0
=> I(t)R=UC(t)
UC
I
U C (t )
R
Am Anfang der Entladung: I(0)R=U0
U0
R
I
I=
U (t )
I (t ) = C
R
UC
R
ΔU C
1
=−
UC
Δt
RC
ΔQ = - I Δt
t
Q
U0
UC=UR
UC =
Q
C
t
ΔU C =
ΔQ
C
ΔU C
~ UC
Δt
Änderungsgeschwindigkeit der
Spannung (UC) ist proportional zur UC .
=> Exponentialfunktion!
t
I (0) =
U C = U 0e
−
t
τ
τ = RC
U0
R
U C = U 0e
−
t
τ = RC
τ
Zeitkonstante
UC
U0
UC
e
τ
t
Wechselspannung
Scheitelwert
Wechselspannungskreis
u
≈
u (t ) = u) sin (ωt )
Kreisfrequenz:
u
ω=2π f
i
R
u)
t
− u)
u
u ( t ) = u) sin( ω t )
t
T
T
T=
1
f
i
)
i (t ) = i sin(ωt )
t
P
Pmax
T
t
Kondensator im Wechelstromkreis
Pmax
Pmax
2
u
≈
t
T
Q
u = UC =
C
)
Q = C ⋅ u = C ⋅ u sin(ωt )
i
Durchschnittliche Leistung:
)
)
Pmax u) i
u) i
P=
=
=
= U eff I eff
2
2
2 2
)
u
Effektive Spannung:
U eff =
)2
i
Effektive Stromstärke:
I eff =
2
Δ sin(ωt )
= ω cos(ωt )
Δt
) )
i = u ⋅ C ⋅ω
u)
1
= XC
)=
i ωC
C
i=
u
t
i
t
T
Zusammenfassung:
u
≈
i
XC =
I eff
XC ≠
u
i
u
≈
i
R
Kapazitiver Widerstand
U eff
ΔQ
) Δ sin(ωt ) )
= Cu
= i cos(ωt )
Δt
Δt
u u) U eff
=)=
i i
I eff
C
u) U eff u
≠
XC = ) =
i
I eff
i
u und i in
gleicher Phase
i eilt sich im
Vergleich zum u
R=