Proseminar Genetische und Evolutionäre Algorithmen

Proseminar
Genetische und Evolutionäre Algorithmen
Genetische Algorithmen – Grundkonzept und genetische Operatoren
Vortragender: Frank Förster
Datum: 29.04.02
Inhaltsverzeichnis
1 Einleitung................................................................................................................................................1
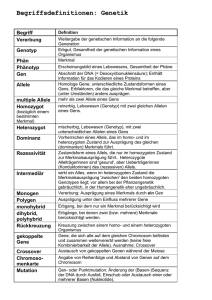
2 Grundbegriffe..........................................................................................................................................2
2.1 Individuum/Chromosom..................................................................................................................2
2.2 Gen..................................................................................................................................................2
2.3 Allel.................................................................................................................................................2
2.4 Population........................................................................................................................................3
2.5 Länge (eines Chromosoms).............................................................................................................3
2.6 Genotyp...........................................................................................................................................3
2.7 Phänotyp..........................................................................................................................................3
3 Grundgerüst eines Genetischen Algorithmus..........................................................................................3
4 Codierung / Lösungsrepräsentation.........................................................................................................4
5 Bewertungs− und Fitnessfunktion...........................................................................................................5
6 Selektion (Heiratsschema).......................................................................................................................6
6.1 Selektionsalgorithmen.....................................................................................................................6
6.2 Auswahlalgorithmen........................................................................................................................7
7 Rekombination/Crossover.......................................................................................................................7
7.1 One−Point−Crossover (1−Punkt−Crossover)..................................................................................8
7.2 N−Point−Crossover (N−Punkt−Crossover).....................................................................................8
7.3 Uniform Crossover..........................................................................................................................9
7.4 Shuffle Crossover............................................................................................................................9
7.5 Diagonal Crossover.......................................................................................................................10
7.6 Sequenzoperatoren.........................................................................................................................10
7.6.A Uniform Order−Based Crossover.........................................................................................11
7.6.B Edge Recombination.............................................................................................................11
7.6.C 1−Elter−Sequenzoperatoren..................................................................................................12
7.7 Vergleich der verschiedenen Crossover−Operatoren....................................................................13
8 Mutation................................................................................................................................................13
9 Ersetzungs−/Ergänzungsschema...........................................................................................................14
10 Abbildungs− und Literaturverzeichnis................................................................................................14
1 Einleitung
Genetische Algorithmen − im folgenden GAs genannt − sind ein Teilgebiet oder eine Untermenge der
Evolutionären Algorithmen (EA), sie stellen momentan sogar deren größtes Teilgebiet dar. In dieser
Funktion stehen sie neben den Evolutionsstrategien (ES), der Evolutionären Programmierung (EP) und
der Genetischen Programmierung (GP). Die GP stellt im engeren Sinne eine spezielle Variante der GAs
dar, welche jedoch einen sehr eigenständigen Ansatz verfolgt und deshalb eine besondere Bedeutung
erlangt hat.
Die Unterscheidung in die Teilgebiete ist hauptsächlich durch die Geschichte bedingt. Die Gebiete
nahmen quasi parallel von unterschiedlichen Personen aus ihren Anfang (die GAs z.B. von John
Holland aus, die ES von Ingo Rechenberg aus). Trotz der relativ hohen Ähnlichkeit der vier
Untergebiete existieren natürlich inhaltliche Unterschiede bzw. Unterschiede, die vor allem die
Schwerpunkte der jeweiligen Gebiete betreffen.
Daneben kann man auch eine Blockeinteilung in den „Genetik−Bereich“, also in Genetische
Algorithmen und Genetisches Programmieren und in den Evolutions−Bereich, also die verbleibenden
zwei Teilgebiete vornehmen, um auf eine erhöhte Ähnlichkeit der jeweiligen Gebiete hinzuweisen.
Die GA−“Anhänger“ (und auch die GP−“Anhänger) legen besonderen Wert auf die problemspezifische
Codierung des vom Algorithmus zu „lösenden“ bzw. zu approximierenden Optimierungsproblems, was
die ES− und ER−“Anhänger“ fast vollständig ignorieren.
GAs kodieren ihre Individuen traditionell in Binärstrings (was man darunter versteht, wird im nächsten
Abschnitt genauer erläutert), wohingegen bei den ES und der EP bevorzugt reelle Vektoren verwendet
werden. GAs benutzen damit traditionell die breitest mögliche, ES hingegen die kompakteste aller
Codierungsmöglichkeiten. In zunehmendem Maße verwenden jedoch neuere GA−Anwendungen
ebenfalls eine von der binären Kodierung abweichende Kodierungsform.Generell kann man sagen, dass
sich nicht an ein festes Schema gehalten wird, sondern immer erst im konkreten Einzelfall, in dem ein
Genetischer Algorithmus angewendet werden soll, entscheiden wird, wie die problem−
charakterisierenden Entscheidungsvariablen kodiert werden.
Ein weiterer Hauptunterschied zwischen den unterschiedlichen Teilgebieten der EAs zeigt sich darin,
wie die Individuen selektiert werden. GAs und EP nehmen eine stochastische Selektion vor. Das heißt,
das prinzipiell auch die an der Fitnessfunktion gemessenen schlechtesten Individuen eine Chance auf
Fortpfanzung also auf Weitergabe ihrer Genetischen Information haben. Bei den ES ist dies nicht der
Fall. Die Selektion wird deterministisch vorgenommen, so dass nur die Individuen mit der besten
Fitness ihre Gene weitergeben. Desweiteren arbeitet man bei GAs mit fixen Populationsgrößen, die
Größe der Population bei ES ist variabel.GA−Anhänger schenken auch dem Cross−Over besondere
Aufmerksamkeit, wohingegen ES−Anhänger ihren Augenmerk eher auf Mutation und Cross−Over als
Suchoperator richten.
Dieser Vortrag beschäftigt sich, wie sein Titel schon vermuten läßt, mit den Grundlagen Genetischer
Algorithmen. Die anderen drei Teilgebiete der Evolutionären Algorithmen werden in den folgenden
Vorträgen behandelt.
Einleitung 1
2 Grundbegriffe
Abbildung 1: Abbildung von Entscheidungsvariablen auf ein Chromosom
2.1 Individuum/Chromosom
Unter einem Individuum bzw. einem Chromosom versteht man im Zusammeenhang mit genetischen
Algorithmen einen binären Vektor (binären String), also ein Element aus {0,1}n.
Die Gleichsetzung der beiden Begriffe Individuum und Chromosom verwirrt anfangs ein wenig, da man
von der Biologie her ja weiß, dass jede Eukaryotenart eine charakteristische Anzahl an Chromosomen
besitzt. Es handelt sich in der Natur also um eine 1:n−Beziehung (ein Individuum – mehrere
Chromosomen, im Fall des Menschen 1 – 46). Im Zusammenhang mit Genetischen Algorithmen wird
allerdings darüber hinweggesehen und der eine Begriff mit dem anderen gleichgesetzt. Es gibt auch
einige, wenige GA−Anwendungen, bei denen Individuen durch mehrere Chromosomen codiert werden,
aber standardmäßig identifiziert man die beiden Begriffe miteinander. Dies rührt vielleicht daher, dass
die 1:n−Beziehung für den Vererbungsmechanismus als unwesentlich angesehen wird. Das Individuum
kodiert eine mögliche und gültige Lösung des zu optimierenden Problems.
2.2 Gen
Unter einem Gen versteht man eine bestimmte Stelle des Chromosoms bzw. einen bestimmten
Abschnitt / eine bestimmte Sequenz des Chromosoms. Das Chromosom <1,0,1,1> enthält somit vier
Gene, das Chromosom <1,0,<1,0,1>,1> ebenfalls. Ob man unter einem einzelnen Gen eine einzelne
Stelle oder einen ganzen Abschnitt versteht, geht aus dem jeweiligen Kontext hervor.
2.3 Allel
Ein Allel bezeichnet die konkrete Ausprägung eines Gens. Betrachtet man das Gen als Variable, so ist
das Allel der Wert der Variablen. Bezeichnen die betrachteten Gene einzelne Stellen eines Binärstrings
und keine Sequenzen, so können die jeweiligen Allele natürlich nur die Werte 0 und 1 annehmen.
Grundbegriffe 2
2.4 Population
Als Population bezeichnet man eine Menge strukturell gleichartiger Individuen. Mit Genetischen
Algorithmen wird durch Anwendung genetischer Operatoren (also im Wesentlichen durch Cross−Over
und Mutation) versucht, bessere Lösungen für ein betrachtetes Problem zu finden. Man arbeitet dabei
stets auf einer ganzen Population und nie mit einzelnen Individuen.
2.5 Länge (eines Chromosoms)
Unter der Länge eines Chromosoms versteht man die Länge des Binärvektors also die Anzahl der Gene
eines Individuums.
2.6 Genotyp
Die codierte Lösung/ der codierte Vektor der Entscheidungsvariablen. Der Genotyp ist damit von der
gewählten Codierungsmethode abhängig. Der Ausdruck hat in der Biologie besondere Bedeutung da
eine befruchtete Eizelle einen doppelten (diploiden) Chromosomensatz besitzt und daher jedes Gen
doppelt vorhanden ist. Es ist deshalb oft unklar welches der beiden in Frage kommenden Gene für eine
bestimmtes Merkmal verantwortlich ist.
2.7 Phänotyp
Die decodierte Lösung/ der decodierte Vektor der Entscheidungsvariablen. Der Phänotyop ist von der
gewählten Codierungsmethode unabhängig. Die Ausprägung des dominanten Gens, also das was letzten
Endes sichtbar wird bzw. dominiert, ist im Falle von GAs der tatsächliche, für die Optimierungsaufgabe
maßgebliche Wert der Entscheidungsvariablen.
3 Grundgerüst eines Genetischen Algorithmus
Genetische Algorithmen sind von ihrer Grundstruktur her immer gleichartig aufgebaut und können in
folgende Subroutinen aufgeteilt werden:
1. Codierung des zu optimierenden Problems, also Abbilden des Problems auf ein (binär) kodiertes
Chromosom.
2. Erzeugung und zufällige Initialisierung einer Population (von Individuen). => Generation 0
3. Wiederholung der folgenden Subroutinen bis Abbruchkriterium erreicht:
4. Bewertung der einzelnen Individuen mit Hilfe einer Bewertungsfunktion. Evtl. Berechnung der
Fitness der einzelnen Individuen mit Hilfe einer Fitnessfunktion, insofern sich diese von der
Bewertungsfunktion unterscheidet.
5. Selektion der (Eltern)Paare oder (Eltern)Subpopulation gemäß einer gewählten Selektionsvariante
und Erzeugung der Nachkommen durch eine gewählte Rekombinationsvariante (Cross−Over).
6. Mutation der erzeugten Nachkommen (die natürlich auch durch Chromosomen repräsentiert sind).
7. Ergänzung der neuen Population bzw. Ersetzen der Elemente der aktuellen Generation nach einem
Grundgerüst eines Genetischen Algorithmus 3
gewählten Ersetzungsschema und Überprüfen der Abbruchbedingung (evtl. Generationszähler
inkrementieren, falls vorhanden).
Man könnte die Selektion und Replikation in Punkt fünf nochmals in zwei separate Unterpunkte
einteilen, was jedoch am Grundalgorithmus nichts ändert.
Die fettgedruckten Subroutinen mit Ausnahme der Codierung werden auch als Genetische Operatoren
bezeichnet. Sie werden zumeist auf das jeweilige Problem angepasst und unterscheiden sich somit von
Anwendung zu Anwendung. Sie stellen die Drehregler dar, mit welchen der oben vorgestellte
Grundalgorithmus auf die zu bewältigende Aufgabenstellung eingestellt wird. Auf die verschiedenen
Möglichkeiten an Operatoralternativen und die damit verbundenen Probleme wird im folgenden
genauer eingegangen.
4 Codierung / Lösungsrepräsentation
Wie schon eingangs erwähnt richten die Anhänger der GAs ein besonderes Augenmerk auf die
Codierung eines Problems, also auf die Abbildung der Entscheidungsvariablen eines Problems auf ein
Chromosom.
Eine interessante Codierungsvariante wird in der Genetischen Programmierung eingesetzt. Hier werden
die Individuen nicht mehr durch einen einfachen Vektor repräsentiert, sondern durch lauffähige
Computerprogramme. Dies hängt mit der vom Gründer dieser speziellen GA−Richtung John R. Koza
propagierten Motivation zusammen, Computer zu selbstlernenden Systemen zu machen, d.h. die
Möglichkeit zu schaffen, Probleme durch Computer lösen zu lassen, für die sie nicht explizit
programmiet wurden. Auf das Thema der GP wird in einem der noch folgenden Vorträge genauer
eingegangen.
Die „normale“ binäre GA−Codierung der Choromosomen über Bitverktoren verwendet bevorzugt den
Gray−Code anstelle des Standard−Binärcodes. Der Grund dafür ist einerseits die z.T. große
(durchschnittliche) Hamming−Distanz des Standardbinärcodes, andererseits aber auch die
unterschiedliche Wertigkeit zwischen benachbarten Stellen.
Unter der Hamming−Distanz versteht man den Abstand zwischen zwei gültigen Codeworten bzw. die
Anzahl der Bits, die man invertieren muss, um von einem gültigen Codewort zu einem anderen zu
gelangen. Die Hamming−Distanz benachbarter, binär dargestellter natürlicher Zahlen im
Standardbinärcode kann dabei beliebig groß werden, wenn man den zulässigen Zahlenbereich nur groß
genug wählt. Dies erschwert die Konvergenz eines Genetischen Algorithmus unnötig, also die
verstärkte Suche in erfolgsversprechen Gebieten des Suchraumes.
Ein kleines Beispiel zur Verdeutlichung: Die Hamming−Distanz zwischen den binären
Repräsentationen von beispielsweise 7 und 8 beträgt vier (0111 → 1000), da vier Bits invertiert werden
müssen. Die beiden Werte liegen also was ihre Hamming−Distanz betrifft wie auch von der
„genetischen Ähnlichkeit“ her bezüglich des Standardbinärcodes recht weit auseinander, obwohl sie
nahe beiander liegende Werte repräsentieren. Auf der anderen Seite haben beispielsweise die Zahlen
100001 und 000001 (also 33 und 1) lediglich einen Abstand von 1. Eine zufälllige Mutation könnte also
die eine Zahl in die andere überführen und die durch diesen Wert repräsentierte Entscheidungsvariable
wesentlich verschlechtern oder verbessern. Es sind also große Sprünge im Phänotyp möglich.
Die unterschiedliche Wertigkeit der Stellen im Standardbinärcode ist offensichtlich. Bei einer durch
eine Sequenz repräsentierten Entscheidungsvariablen – unabhängig davon ob man nun die binäre
Sequenz als einzelnes Gen definiert oder eine Sequenz von Genen zur Kodierung heranzieht – ergibt
sich folgendes Problem: Je weiter vorne man sich in in der Sequenz befindet, desto größer ist die
Codierung / Lösungsrepräsentation 4
Zweierpotenz und desto höher ist die Wertigkeit der betreffenden Stelle. Eine Mutation die weiter vorne
in der Sequenz ansetzt hat damit natürlich für den codierten Wert ein größeres Gewicht als eine weiter
hinten ansetzende Mutation. Dieses Ungleichgewicht müsste durch eine geringere
Mutationswahrscheinlichkeit auf den vorderen Stellen ausgeglichen werden. Beim Crossover, dem
wichtigsten Operator der GAs, auf den später noch näher eingegangen wird, liegt die Problematik für
eine aus beiden Elternteilen gebildete Sequenz ähnlich. Der für den vorderen Teil zuständige Elternteil
hätte einen größeren Einfluss auf die Entscheidungsvariable als der hintere Teil, was aber vermieden
werden sollte.
Der Standard−Binärcode verletzt somit bei der Rekombination und Mutation das von Rechenberg
eingeführte Prinzip der strengen Kausalität, welches aussagt, dass eine kleine Ursache auch nur eine
kleine Wirkung nach sich ziehen sollte.
Der Gray−Code hingegen hat immer eine Hammingdistanz von 1. Der Graycode löst zwar nicht alle bei
GAs auftretenden Codierungsprobleme,aber er reduziert sie zumindest deutlich.
Im Folgenden ein kleines Beispiel von Standardbinärcode und Graycode mit einer Beispielmutation
(d = Hamming−Distanz (k, k−1)):
dezimal
Standardbinärcode
Gray−Code
0
000
000
1
001
(d = 1)
001
(d = 1)
2
010
(d = 2)
011
(d = 1)
3
011
(d = 1)
010
(d = 1)
4
100
(d = 3)
110
(d = 1)
gegeben: dezimal 105 und Mutation an vierter Stelle der Sequenz des Genotyps:
Standardbinärcode:
Graycode
:
1101001 → 1100001 (dez. 97, ∆ : 8)
1011101 → 1010101 (dez. 102, ∆ : 3)
Die gezeigte geringere Veränderung des Wertes einer Variablen durch Mutation an einer Stelle bei
Einsatz von Gray−Codierung trifft jedoch nicht immer zu. Würde man beispielsweise bei dezimal drei
im Graycode das zweite Bit kippen, käme man zur Null, bei der Standardbinärcodierung zur Eins, was
zeigt dass die mutationsbedingten Veränderungen eines Allels bei Einsatz von Gray−Codierung nicht
immer geringfügiger sind.
5 Bewertungs− und Fitnessfunktion
Die Bewertungsfunktion misst die Güte eines gegebenen Individuums bezüglich des zu optimierenden
Zieles, die Fitnessfunktion hingegen bewertet seine Chancen zur Fortpflanzung. In einigen Fällen
werden beide Funktionen gleichgesetzt, da es auf der Hand liegt, dass die am Optimum gemessenen
besten Individuen auch die besten Chancen zur Replikation zugestanden bekommen sollten. Häufiger
ist es jedoch so, daß die Fitnessfunktioneine Funktion der Bewertung darstellt.
Gängig sind dabei die sog. Proportionale oder Lineare Fitness, bei der die Fitness eines Chromosoms in
direkter Proportionalität zur Bewertung steht (Propfit(I) := a*I/B, wobei I die Bewertung eines
Individuums sei, B die Summe der Bewertungen aller Individuen und a ein beliebiger Faktor).
Wie die Bewertungsfunktion einer GA−Anwendung aussieht, ist problemspezifisch. Es existieren keine
allgemeinen diese Funktion betreffenden Regeln.
Bewertungs− und Fitnessfunktion 5
6 Selektion (Heiratsschema)
Die Selektion kann in einen Selektionsalgorithmus und in einen Auswahlalgorithmus aufgeteilt werden.
Der Selektionsalgorithmus weist dabei jedem Individuum einen Wahrscheinlichkeitswert für dessen
Replikation zu. Dieser Wert ist dabei zunächst nur ein Erwartungswert E(I) = µ * ps(I), wobei µ die
Populationsgröße und ps(I) die Selektionswahrscheinlichkeit des betreffenden Individuums ist. E(I) gibt
also die zu erwartende Anzahl der Kopien des Individuums im sog. mating pool an.
Wie das Wort „erwartet“ schon andeutet wird die tatsächliche Anzahl der Kopien des Individuums im
mating pool vom Auswahlalgorithmus bestimmt. Der Unterschied zwischen erwarteter und
tatsächlicher Anzahl wird dabei als „spread“ bezeichnet.
6.1 Selektionsalgorithmen
Ein gängiger Selektionsalgorithmus ist die fitnessproportionale Selektion, bei der ps(I) direkt
Ij
proportional zur Fitness des jeweiligen Chromosoms ist. ps =
n
Ij
j 1
Φ ist dabei die Bewertungsfunktion, I ein Individuum und j der Index/die Nummerierung der
Individuen (bei n Individuen insgesamt).
Die wichtigsten Alternativen zur fitnessproportionalen Selektion sind rangbasierte Selektion (ranking)
und Wettkampfselektion (tournament selection). Der Grund für alternative Algorithmen ist der
verhältnismäßig niedrige Selektionsdruck der fitnessproportionalen Selektion. Je höher der
Selektionsdruck ist, desto schneller konvergiert der Algorithmus und desto schneller wird ein u.U.
lokales Optimum gefunden. Als Maß für den Selektionsdruck wurde die sog. takeover time eingeführt.
Sie ist definiert als diejenige Anzahl an Generationen, die benötigt wird um mit einem gegebenen
Selektionsalgorithmus bei alleiniger Anwendung der Selektion eine Population zu generieren, die x−1
Kopien des besten Individuums der Ausgangspopulation enthält, wenn x die (fixe) Populationsgröße ist.
Bei der Rangbasierten Selektion steht die Selektionswahrscheinlichkeit nicht mehr in direktem
Verhältnis zur Fitness. Statt dessen werden die Individuen einer Population nach absteigendem
Fitnesswert sortiert und durchnummeriert. Die Selektionswahrscheinlichkeit steht dann mit der so
entstandenen Rangzahl eines Individuums im Verhältnis. Der Selektionsdruck kann dabei über einen
dem höchstrangigen Individuum zugeordneten Erwartungswert Emax, der in Grenzen wählbar ist,
eingestellt werden.
Die Wettkampfselektion stellt Selektions− und Auswahlalgorithmus zugleich dar. Hier werden jeweils
z Individuen (2 ≤ z ≤ x, x = Pop.größe) bei gleicher Selektionswahrscheinlichkeit aus der Population
gezogen, deren Fitness miteinander verglichen und das Beste in den mating pool kopiert. Dies wird x−
mal durchgeführt. Über z kann der Selektionsdruck direkt eingestellt werden: je größer z, umso höher
ist der Selektionsdruck. Die Wettkampfselektion birgt allerdings die Gefahr, dass im Extremfall x
identische Individuen in den mating pool kopiert werden. (s.a. Auswahlalgorithmus roulette wheel).
6.2 Auswahlalgorithmen
Der am weitesten verbreiteste Auswahlalgorithmus ist die sog. roulette wheel selection (auch Roulette−
Prinzip genannt). Anschaulich entspricht dieser Algorithmus einem Glückrad, das in x Abschnitte
unterteilt wird, wenn x die Zahl der Individuen einer Population ist. Die Breite jedes Abschnitts ist
dabei direkt proportional zu der Selektionswahrscheinlichkeit des zugehörigen Individuums. Nun wird
am Rad x mal gedreht und so die Eltern für die nächste Generation bestimmt. Dabei hat ein Individuum
Selektion (Heiratsschema) 6
natürlich umso bessere Chancen ausgewählt zu werden, je höher seine Fitness ist. Im Extremfall besteht
allerdings wie schon bei der Wettkampfselektion die Gefahr, dass x gleiche Individuen ausgewählt
werden. Roulette wheel selection hat damit einen verhältnismäßig hohen spread, ist aber dennoch das
verbreitetste Verfahren.
Einen minimalen spread hat das sog. Stochastic Universal Sampling (SUS). Wieder geht man von
einem Glückrad aus wie schon bei der roulette wheel selection. Auch hier ist die Breite des jeweiligen
Abschnitts proportional zum Erwartungswert E(I) des jeweiligen Individuums I und damit auch zur
Selektionswahrscheinlichkeit. Allerdings werden hier im Gegensatz zur roulette wheel selection x in
gleichmäßigem Abstand um das Glücksrad angeordnete Zeiger verwendet (x wieder Pop.größe). Das
Rad wird hier allerdings nur einmal gedreht und von jedem Individuum werden exakt soviel Kopien in
den mating pool kopiert wie Zeiger auf den zugehörigen Abschnitt zeigen. Dadurch kann
ausgeschlossen werden, dass x mal dasselbe Individuum im mating pool auftritt.
Abbildung 2: SUS Auswahlalgorithmus
7 Rekombination/Crossover
Der wichtigste Suchoperator bei Genetischen Algorithmen ist der Crossover−Operator. Er beschreibt
die Art und Weise, wie das neue Individuum aus zwei oder mehreren „alten“ Chomosomen, also
Chromosomen der Elterngeneration gebildet werden können. Die Eltern werden stochastisch aus dem
mating pool ausgewählt. Wir gehen zunächst von zwei Eltern aus und besprechen Mehr−Elter−
Rekombinationen weiter unten, da sie doch eher die Ausnahme sind. Ob überhaupt ein Crossover
zwischen zwei Eltern stattfindet oder nicht, wird durch die Crossover−Wahrscheinlichkeit pc festgelegt:
Üblicherweise ist pc ≥ 0,6 (nach Empfehlung), womit ein Crossover wahrscheinlicher ist als kein
Crossover. In der Praxis zieht man also eine Zufallszahl u, die im Intervall [0,1[ liegt und vergleicht sie
dann mit dem gewählten pc . Ist die gezogene Zufallszahl größer als pc findet ein Crossover statt,
ansonsten werden die Elternchromosomen so wie sie sind dem Mutationsoperator übergeben, der in der
Reihenfolge der Subroutinen auf das Crossover folgt. Bis hierhin gleichen sich noch alle Crossover−
Varianten, das weitere Vorgehen unterscheidet sich jedoch je nach Variante.
Rekombination/Crossover 7
7.1 One−Point−Crossover (1−Punkt−Crossover)
Dieses Verfahren wählt zunächst zufällig einen Crossover−Punkt, der zwischen 1 und L−1 (L = Länge)
liegt, also eine Grenze zwischen zwei Genen referenziert. Abhängig von diesem Punkt werden nun die
Gene der beiden Chromosomen rekombiniert, indem Teile ausgetauscht werden. Alle Gene, die sich
links vom Crossover−Punkt c befinden (Genindex i < c) werden, vom ersten Elternteil übernommen,
die restlichen Gene des neuen Individuums werden vom zweiten Elternteil kopiert. Beim zweiten
Nachkommen wird analog vorgegangen, jedoch mit vertauschen Elternteilen.
7.2 N−Point−Crossover (N−Punkt−Crossover)
Das N−Punkt−Crossover funktioniert vom Prinzip her genau gleich wie das one−point−crossover, mit
Außnahme der Tatsache, dass n statt nur einem crossover−Punkt bestimmt werden. Üblicherweise ist n
aus Symmetriegründen eine gerade Zahl. Der erste Teil der neuen Chromosomen, also diejenigen Gene
bis zum ersten crossover−Punkt, werden wieder vom asoziierten Elternteil übernommen, der zweite
Teil vom zweiten Elter, der dritte wieder vom ersten Elter etc. .
Abbildung 3: N−Point−Crossover
7.3 Uniform Crossover
Beim Uniform Crossover wird für jedes Bit einzeln geprüft, ob es zwischen den Elternteilen
ausgetauscht wird oder nicht. Maßgeblich ist dabei eine festzulegende Wahrscheinlichkeit pux und eine
bitbezogene Wahrscheinlichkeit Uz (z = 1, 2, ..., L). Ist pux ≥ Uz werden die beiden Bits an Position z
zwischen den Elternteilen ausgetauscht, ansonsten nicht.
Rekombination/Crossover 8
Abbildung 4: Uniform Crossover
7.4 Shuffle Crossover
Das Shuffle Crossover stellt
eine Erweiterung des 1−
Punkt− bzw. N−Punkt−
Crossovers, um einen
zusätzlichen
shuffle−/unshuffle−Schritt
dar. Die Gene werden hierbei
zunächst durchnummeriert
und danach durchmischt
(shuffle). Auf den
durchmischten Chromo−
somen wird dann ein one−
bzw. n−point−crossover
durchgeführt. Abschließend
werden die Gene anhand
ihrer Nummerierung wieder
entmischt (unshuffle).
Abbildung 5: Shuffle Crossover
7.5 Diagonal
Crossover
Das Diagonal Crossover ist ebenfalls eine Erweiterung des N−Punkt−Crossovers. Allerdings verläuft
hierbei die Erweiterung in eine andere Richtung: Es sind nun mehr als zwei Eltern zulässig; Diagonal
Crossover erzeugt aus i Eltern i Nachkommen. Dies veranschaulicht einmal mehr die Abstraktion, die
die Genetischen Algorithmen vom natürlichen Vorbild vornehmen, denn diese Crossover−Variante
Rekombination/Crossover 9
dürfte in der Natur kaum zu finden sein.
Die i Eltern− und Kinder−Chromosomen werden durch (i−1) stochastisch gewählte Crossover−Punkte
in i Abschnitte unterteilt.Eltern und noch leere Kinder werden separat durchnummeriert. Die Bildung
der Kinder geschieht
nun wie folgt: Der erste
Abschnitt des i−ten
Kinder−Chromosoms
wird mit dem ersten
Abschnitt des
zugehörigen
Elternchromosoms −
also dasjenige Eltern−
Chromosom, das seine
Nummer trägt −belegt
(die Allele dieses
Abschnitts werden in
die entsprechenden
Gene des Kindes
kopiert). Der zweite
Abschnitt des Kinder−
Chromosoms wird mit
Abbildung 6: Diagonal Crossover
den Allelen des zweiten
Abschnitts des i+1−ten
Eltern−Chromosoms belegt, der dritte Abschnitt mit den Allelen des dritten Abschnitts des i+2−ten
Elternchromosoms u.s.w.. Ist das letzte Elternchromosom erreicht, also dasjenige mit der höchsten
Nummer, wird wie in einem Rotationsverfahren wieder beim ersten anfangen.
7.6 Sequenzoperatoren
Sequenzoperatoren sind Suchoperatoren, die auf Codierungen von Permutationen arbeiten bzw. speziell
für diese angepasst wurden. Naheliegenderweise kann man für die Optimierung von Permutationen
nicht die üblichen, oben vorgestellten Operatoren verwenden, denn diese würden bei einer binären
Permutations−Codierung mit hoher Wahrscheinlichkeit ungültige Belegungen der einzelnen Elemente
der Permutation erzeugen. Z.B. wäre die Erzeugung zweier gleicher Zahlen in einer Variablen/einem
Gen ohne weiteres möglich, was in einer Permuation aber unzulässig ist. Deshalb wurden in diesem
Bereich spezielle Cross−Over−Verfahren entwickelt. Man kann die Sequenzoperatoren über die Anzahl
der zum Cross−Over herangezogenen Elternchromosomen klassifizieren. So gibt es 1−Elter−, 2−Elter−,
... oder kurz M−Elter−Sequenzoperatoren. Standard sind bei Permutationsoptimierungen ebenfalls zwei
Eltern, also M = 2.
7.6.A Uniform Order−Based Crossover
Uniform Order−Based Crossover gehört zu den 2−Elter−Operatoren und verläuft vom Prinzip her
analog zum oben beschriebenen Uniform Crossover (dessen Verallgemeinerung für Permutationen es
darstellt). Auch hier wird aus positions−bezogenen Wahrscheinlichkeiten eine binäre Maske generiert,
die darüber bestimmt, welche Permutationselemente (Allele) aus dem ersten Elterchromosom und
welche Permutationselemente aus dem zweiten Elterchromosom in die Nachkommen kopiert werden.
Dazu geht man wie in der Abbildung 7 angedeutet vor: In dem dargestellten Beispiel deutet eine Eins in
Rekombination/Crossover 10
der zufällig generierten Bitmaske an, dass die Allel−
Ausprägung des entsprechenden Gens des ersten
Elters in den ersten Nachkommen kopiert wird. Eine
Null bedeutet die Übernahme des asoziierten Allels
des zweiten Elters in den zweiten Nachkommen.
Nun sind noch einige Stellen (Genpositionen) in den
Chromosomen der Kinder frei, und die Allele der
entsprechenden Eltern (Kind 1−Elter 1, Kind 2
−Elter 2) wurden noch nicht verwendet. Die
fehlenden Gene können jetzt selbstverständlich nicht
einfach mit den Allelen des anderen Elternteils an
dieser Stelle gefüllt werden, da es sonst mit größter
Wahrscheinlichkeit zu unzulässigen Belegungen
kommen würde. Statt dessen werden die noch freien
Allele der Eltern in der entsprechenden Reihenfolge
derselben Allele des anderen Elters angeordnet und
die noch offenen Gene des Kindchromosoms von
links nach rechts (in dieser Reihenfolge aufgefüllt).
Zusammenfassend kann man also sagen, dass das
Uniform Order−Based Crossover Informationen
über die relative Reihenfolge der Allele vererbt.
Abbildung 7: Uniform Oder−Based Crossover
7.6.B Edge Recombination
Bei der Edge Recombination werden im Unterschied zum Uniform Order−Based Crossover
Informationen über (direkte) Nachbarschaftsbeziehungen vererbt. Nachbarschaftsbeziehungen würden
in einem Graph als Kanten dargestellt werden, daher die Bezeichnung.
Die Edge Recombination generiert aus zwei Eltern jeweils nur einen Nachkommen. Die in den Eltern
codierte Nachbarschaftsinformation wird dafür in einer sog. edge table abgelegt. In dieser Tabelle
werden hinter jedem Allel die Nachbarallele aus beiden Eltern aufgelistet. Doppelte
Nachbarschaftsbeziehnungen, also Nachbarschaften die in beiden Elternteilen auftreten, werden dabei
mit einem Minuszeichen gekennzeichnet und beim eigentlichen Cross−Over bevorzugt behandelt. Die
Allele des Kindes werden nun wie folgt bestimmt: Zunächst wählt man zufällig eines der beiden Elter−
Allele an der ersten Genposition und löscht es aus der Auflistung der Nachbarwerte auf der rechten
Seite der Edge table (vgl. Abbildung 8). Anschließend bestimmt man aus der Nachbarschaftsliste des
gewählten Allels ein darauffolgendes Allel (Nachbar des neuen Chromosoms)) nach folgender Priorität:
(1)Zuerst Allele mit Minuszeichen
(2)danach dasjenige Allel mit der kürzesten Nachbarschaftsliste
Sollten dabei mehrere (alte) Nachbar−Allele die gleiche Priorität besitzen, also beispielsweise zwei
Allele mit Minuszeichen bzw. zwei Nachbarn mit gleichkurzer Nachbarschaftsliste, wird unter diesen
eines zufällig bestimmt. Ist auf der anderen Seite die Nachbarschaftsliste eines Allels leer, was vor
allem dann auftritt, wenn schon mehrere Gene des Kinds belegt wurden, wird unter den verbleibenden
Allelen ebenfalls eines zufällig ausgewählt. So belegt man schrittweise die Gene des Kindes bis sein
Chromosom vollkommen bestimmt wurde bzw. die Edge table leer ist.
Rekombination/Crossover 11
Abbildung 8: Edge Recombination
7.6.C 1−Elter−Sequenzoperatoren
Bei den 1−Elter−Sequenzoperatoren handelt es sich streng genommen nicht mehr um Cross−Over−
Operatoren, da mangels einem zweitem Elter kein Cross−Over stattfinden kann. Man könnte sie eher zu
den permutationsspezifischen Mutations−Operatoren zählen. Sie werden im folgenden jeweils ohne
Bild erläutert; die Operator−Bezeichnungen sind dabei fett gedruckt.
Zu den 1−Elter−Sequenzoperatoren zählt der Zweiertausch, der, wie der Name schon besagt, zwei
Allele vertauscht. Die zu tauschenden Gene, also die Positionen der Allele im Binärstring, werden
stochastisch bestimmt. Alle Gene besitzen bezüglich ihrer Auswahl die gleiche Wahrscheinlichkeit 1/L.
Analog existieren Dreiertausch, Vierertausch etc..
Beim Verschiebungsoperator werden in Analogie zum 2−Punkt−Crossover stochastisch zwei Punkte
bestimmt, ein Anfangs− und ein Endpunkt. Das von diesen beiden Punkten eingegrenzte Sequenzstück
wird um eine zufällig bestimmte Anzahl an Gen−Positionen auf dem Chomosom nach rechts
verschoben, die dahinter liegenden Gene rücken um dementsprechend viele Postitionen nach vorne.
Dabei wird das Chomosomende zirkulär auf den seinen Anfang angebildet.
Die Inversion dreht ein zwischen zwei stochastisch bestimmten Punkten liegendes Sequenzstück um:
das hinterste Gen wird innerhalb der Sequenz zum ersten, das zweithinterste zum zweitvordersten etc..
Der Scramble Sublist Operator permutiert die zwischen zwei stochastisch bestimmten Punkten
liegenden Allele in zufälliger Reihenfolge.
Rekombination/Crossover 12
7.7 Vergleich der verschiedenen Crossover−Operatoren
Man vergleicht verschiedene Crossover−Operatoren üblicherweise auf der Grundlage zweier,
unerwünschter Charakteristikas: positional bias und distributional bias.
Unter positional bias versteht man die Abhängigkeit der Wahrscheinlichkeit eines Genaustauschs
durch eine Crossover−Operation von der Position der Codierung der Gene im Chromosom. Besitzt ein
Crossover−Operator ein großes postitional bias, so werden gewisse Gene mit größerer
Wahrscheinlichkeit zwischen den Eltern ausgetauscht als andere. So hat z.B. das 1−Punkt−Crossover
ein relativ großes postitional bias, da die Wahrscheinlichkeit eines Austausch mit wachsender
Positionsnummer zunimmt.
Distributional bias hat ein Crossover−Operator dann, wenn die erwartete Anzahl der beim Crossover
ausgetauschten Gene keiner Gleichverteilung zwischen 1 und L−1 unterliegt. 1−Punkt−Crossover
schneidet diesbezüglich sehr gut ab: es besitzt kein distributional bias. Nachfolgend ein kleiner
Vergleich von ausgewählten auf Binärstings arbeitenden Crossover−Operatoren:
positional bias
distributional bias
1−Punkt−Crossover
viel
kein
N−Punkt−Crossover
weniger als 1−Punkt−Crossover
mit steigendem N zunehmend
Uniform−Crossover
kein
sehr viel (pux*L) → zunehmend
mit steigender Länge
Shuffle−Crossover
kein
entspricht dem dist. bias des
gewählten Basis−Operators (N−
Punkt, 1−Punkt)
8 Mutation
Wie schon erwähnt spielt die Mutation bei den Genetischen Algorithmen eher die Rolle eines
Hintergrundoperators. Dies drückt sich in einer niedrigen Mutationswahrscheinlichkeit von einzelnen
Bits aus. Verbreitet sind Wahrscheinlichkeiten von pm = 0,01 und pm = 0,001. Der Trend geht allerdings
dahin, dass der Mutation auch bei Genetischen Algorithmen verstärkte Aufmerksamkeit geschenkt
wird.
Unter einer Mutation kann dabei das Kippen eines Bits, also der Übergang zum komplementären Allel
eines Gen verstanden werden, aber auch die zufällige Neubestimmung eines Bits. Die letztgenannte
Variante verringert die Mutationswahrscheinlichkeit noch weiter, da bei binärer Codierung im Mittel
die Hälfte der neu gesetzten Bits identisch mit dem alten Bit sind.
Bei geringer Mutationswahrscheinlichkeit und langen Chromosomen wirkt sich die Mutation im
Normalfall kaum auf die Güte aus. Ungleiche Mutationswahrscheinlichkeiten für unterschiedliche Gen−
Positionen sind ebenfalls keine Ausnahme, insbesondere bei einer Standardbinärcodierung. Hier kann
eine an die einzelnen Bits angepasste Mutationswahrscheinlichkeit die positionabhängige Wertigkeit
von Genen teilweise kompensieren. Generell sollen Mutationen eine zu frühzeitige Konvergenz des
Algorithmus verhindern, indem sie Inhomogenität und Divergenz in die Population bringen. Sie wirkt
somit dem Selektionsdruck entgegen.
Mutation 13
9 Ersetzungs−/Ergänzungsschema
Nachdem neue Individuen durch die bisher beschriebenen Schritte erzeugt wurden, muss entschieden
werden, welcher Anteil der alten Individuen durch neue ersetzt werden soll. Die einfachste Variante
hierbei ist das general replacement, bei dem alle alten Individuen durch neue ersetzt werden. Dieses
Vorgehen besitzt allerdings den Nachteil, dass dadurch potentiell das beste Indviduum der
Vorgängergeneration verloren geht und auch die mittlere Güte der Gesamtpopulation abnehmen kann.
Auf der anderen Seite läuft ein genetischer Algorithmus mit general replacement jedoch nie in Gefahr,
sich auf einige wenige, sehr gute Individuen einzuschießen, und damit möglicherweise seinen
Suchraum negativ einzuschränken und in einem Suboptimum steckenzubleiben. Behält man ein oder
wenige der besten Individuen der alten Generation bei, so spricht man von Elitismus bzw. vom Prinzip
der Eliten. Dieser birgt allerdings, wie soeben schon angedeutet, die Gefahr, dass der Algorithmus zu
früh konvergiert, wenn einige, wenige Individuen sehr viel besser sind als die anderen. Dadurch werden
potentiell bessere Lösungen u.U. nicht mehr gefunden. In einer abgeschwächten Form, man spricht
auch von schwachem Elitismus, unterwirft man die beizubehaltenden Individuen der Mutation, bevor
man sie in die neue Generation übernimmt. Betrachtet man die Ersetzungs−Problematik von der
anderen Seite aus, so könnte man genau so gut fragen, wieviele der neuen Elemente durch Individuuen
der Vorgängergeneration ersetzt werden sollen. Man spricht dann von einem delete−n−last−Schema,
falls die n schlechtesten, generierten, neuen Individuen durch alte ersetzt werden. Wird dabei die alte
Population größenteils übernommen, und ist Anzahl der neuen Individuen sehr viel kleiner als die
Populationsgröße, so spricht man auch von einem „Steady−state“ Ersetzungsschema. Darauf geht
allerdings der nächste Vortrag näher ein.
10 Abbildungs− und Literaturverzeichnis
verwendete Literatur:
Nissen, Volker; Einführung in Evolutionäre Algorithmen; Vieweg Verlag; 1997
Schöneburg, E., Heinzmann, F., Feddersen, S.; Genetische Algorithmen und Evolutionsstrategien;
Addision−Wesley; 1996
Campbell, Neil A.; Biologie; Spektrum Akademischer Verlag; 1997
Alle Abbildungen sind dem oben genannten Buch von Volker Nissen entnommen.
Abbildungs− und Literaturverzeichnis 14