5.7 Reversibler und irreversibler Prozess im Vergleich

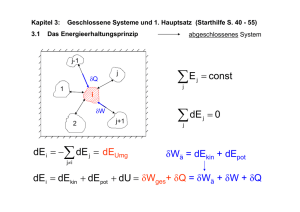
5. Prozessbewertung und zweiter Hauptsatz (Starthilfe S. 58-69)
5.1 Das Prinzip der Irrevesibilität
- bestimmte Richtung der Prozesse
δQ
T1>T2
δWR ≥ 0
T2
- durch Reibung nimmt der Anteil der in Arbeit umwandelbaren Energie ab
- reversibler Prozess als theoretischer Grenzfall
isotherme Kompression
pA
δQ
T=Tu
isotherme Expansion
Fä
+ dFä
Folge von Gleichgewichten
- alle natürlichen Prozesse sind irreversibel
pA
δQ
Fä
- dFä
5.2 Entropie und zweiter Hauptsatz
gesucht wird eine Zustandsgröße zur Beschreibung der Richtung und
des Ablaufes von Prozessen
1. HS: du + pdv = δq + δw R + (p − p SG ) dV mit δw R + (p − p SG ) dV ≥ 0
>
δq 0
<
adiabates System: (du + pdv )ad = δw diss ≥ 0
>0
irreversibler
=0
<0
reversibler
nicht möglicher Prozess
Überführung in eine Zustandsgröße (integrierender Nenner)
du (T, v ) + p (T, v )dv
d ϕ(T, v ) =
N(T, v )
Entropie
dS =
dU + pdV δQ rev
,
=
TTD
TTD
Thermodynamische Temperatur
S
=s
M
TTD = Tid. Gas = T > 0
in
K
nichtadiabate Systeme
- reversibler Prozess: quasistatisch, δw diss = 0
du + pdv = δqrev
bzw.
ds =
du + pdv δqrev >
=
0
T
T <
- realer Prozess:
dS =
δWdiss
dU + pdV δQ (p − p SG )
dV +
=
+
T
T
T
T
Berücksichtigung ΔT = T − Tu für Wärmetransport
δQ
dS =
Tu
⎛1 1 ⎞
p − pSG
δWdiss
+ ⎜⎜ − ⎟⎟δQ +
dV +
T
T
⎝ T Tu ⎠
dS = δS Transp +
2. Hauptsatz:
δSirrev
δSirrev ≥ 0
5.3 Zweiter Hauptsatz für adiabate Gesamtsysteme
(d S )
ges ad
⎞
⎛
⎜
= ⎜ ∑ dS j ⎟⎟
⎠ad
⎝ j
⎛
⎞
⎜
= ⎜ ∑ δS Transp, j + ∑ δSirrev, j ⎟⎟
⎝ j
⎠ad
= (∑ δSirrev, j )ad ≥ 0
(dS )
ges ad
⎛
⎞
⎜
= ⎜ ∑ dS j ⎟⎟ ≥ 0
⎝ j
⎠ad
2. Hauptsatz
5.4 Entropie als Zustandsgröße
- Definition:
1
du + pdv dh − vdp ⎛ δqrev ⎞
ds = dS =
=
=⎜
⎟
M
T
T
⎝ T ⎠quasist.
- Integration: u = u ( T,v ) , p = p ( T,v )
stoffabhängig
⎛
⎞
1
- ideale Flüssigkeiten ⎜ v = = const, du = c ( T ) dT ⎟ :
ρ
⎝
⎠
2
T2
2
c = const
cdT
pdv
s2 − s1 = ∫ ds = ∫
+∫
T
T
1
T1
1
- ideale Gase
T2
T1
(pv = RT, du = c ( T ) dT ) :
c v ( T ) dT v 2 Rdv
s2 − s1 = ∫
+∫
T
T
T1
v1
T2
s2 − s1 = c ln
v
c v = const
s2 − s1 = c v ln
T2
v
T
p
+ Rln 2 = c p ln 2 − Rln 2
T1
v1
T1
p1
5.5 T,s-Diagramm (id. Gase)
T
du + pdv c v dT + pdv
=
T
T
dh − vdp c p dT − vdp
ds =
=
T
T
ds =
Voraussetzung: c p , c v = const
s
Isochore:
Isobare:
s − s1 = c v ln
s − s1 = c p ln
T
T1
T
T1
→
→
T = T1e
s − s1
cv
T = T1e
s − s1
cp
5.6 Zustandsänderungen in adiabaten Systemen (id. Gase)
T
Kompression
T
Expansion
Tds = du + pdv
= dh − vdp
= (δq + δw R )quasistat .
s
isentrope ZÄ (reversibel, adiabat)
s
ds = 0, s = const
Isentropenbeziehungen
1 : du + pdv = 0 → c v dT = −pdv = −
RT
dv
v
→ f (T, v ) = 0
2 : dh + vdp = 0 → c pdT = vdp = −
RT
dp
p
→ ϕ(T, p ) = 0
3 = 2 / 1:
Integration:
(cp, c v , κ = const )
→
cp
cv
=κ=−
vdp
pdv
→ f (T, v ) = 0
Isentropenexponent
pv κ = const = p1v1κ = p2 v 2κ
p = RT / v
v = RT / p
5.7 Reversibler und irreversibler Prozess im Vergleich
Voraussetzung:
rev. Prozess:
durev , dv rev → dsrev
realer Prozess: du = durev
dv = dv rev
dU
= δQrev + δWrev
dQrev = δQ
~ δSTransp
δW − δWrev ≥ 0
= δQ + δW
+ δW − δWrev = TdS
~ δSirrev
Kompr . (δWrev > 0 ) : | δWrev | < | δW |
min. Arbeitsau fwand
Exp.
max. Arbeitsge winn
(δWrev < 0) : | δWrev | > | δW |
Zusammenfassung – Entropie und 2. Hauptsatz
• Definition- und Berechnungsgleichungen der Entropie:
du + pdv dh + vdp δqrev ( δq + δw diss )quasistat.
ds =
=
=
=
T
T
T
T
Integration abhängig vom Stoff
⎛
⎝
- ideale Flüssigkeiten ⎜ ρ =
T2
s2 − s1 = c ln
T1
für
1
⎞
= const, du = cdT ⎟
v
⎠
c = const
(
- ideale Gase c p , c v = const
s2 − s1 = c v ln
)
T2
v
T
p
+ Rln 2 = c p ln 2 − Rln 2
T1
v1
T1
p1
• 2. Hauptsatz:
(
dSges
)
ad
⎛
⎞
= ⎜ ∑ dS j ⎟ ≥ 0
⎝ j
⎠ad
> 0 irreversibel
= 0 reversibel
< 0 nicht möglich
• T,s-Diagramm:
2
∫ T ( s ) ds = q
12
1
= ( q12 )rev
+ w diss,12
= ( w diss,12 )ad