Folien_zur_Vorlesung_Energiesysteme Kapitel_3

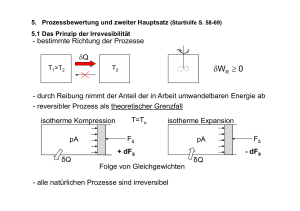
Kapitel 3:
3.1
Geschlossene Systeme und 1. Hauptsatz (Starthilfe S. 40 - 55)
Das Energieerhaltungsprinzip
abgeschlossenes System
j-1
δQ
j
∑E
j
= const
j
1
i
δW
2
j+1
dEi = −∑ dE j = dEUmg
j≠i
∑ dE
j
=0
j
δWä = dEkin + dEpot
dE i = dEkin + dE pot + dU = δWges+ δQ = δWä + δW + δQ
3.2 Arbeit und innere Energie
Voraussetzung: • adiabate Systeme (δQ = 0)
− dEUmg = δW = dE System
• Schwerkraft als einzige äußere Kraft
• Beschränkung auf mechanische Arbeit
3.2.1 Mechanische Arbeit
Scherkräfte
Ö Wirkung einer Kraft
Normalkräfte
G
G
= ∫ F ( s ) ⋅ ds
2
Wmech,12
1
äußere Arbeit δWä
Wirkung auf das thermodynamische System
Systemarbeit δW
Mechanische Arbeit und thermodynamisches System
→ keine Änderung des inneren
Systemzustandes (Änderung
der äußeren Koordinaten)
→ Änderung des inneren
Systemzustandes (dp, dT)
δWmech = δWSystem
δWmech = δWä
p, T
ds
p, T
ds
F
F
−dEUmg
G G
= Fds = Fds = δWmech
3.2.2 Äußere Arbeit
−dEUmg = δWmech = dESystem = d (Ekin + Epot + U)
δWä = dEkin + dEpot
M 2
= dv + Mgdz
2
δWä 1 2
δw ä =
= dv + gdz
M
2
w ä,12
(
)
1 2
2
= v 2 − v1 + g ( z2 − z1 )
2
(Vernachlässigung der
Rotation in dEkin)
spezifische Arbeit
3.2.3 Systemarbeit
- Volumenänderungsarbeit
quasistatische und nichtstatische Zustandsänderung
• quasistatische Zustandsänderung
(→ Folge von Gleichgewichten)
• mechanisches Gleichgewicht
F + pUAK = pSGAK = pAK
• nichtstatische Zustandsänderung
pSG ≠ p (Nichtgleichgewicht)
Ö Diskussion des Druckausgleichs
(mechanisches Gleichgewicht)
im System
Volumenänderungsarbeit - Berechnungsgleichung
δWV = δWmech = ± Fds = −pSGdV( System)
Vorzeichenvereinbarung: • Zufuhr (Kompession)
• Abgabe (Expansion)
δW > 0
δW < 0
quasistatische Zustandsänderung: p SG = p System = p(V )
δWV quasistatisch = δWV = −p ( V ) d V
Volumenänderungsarbeit - Integration
• spezifische Arbeit
w v,12
2
Wv,12 2
=
= ∫ δw v = ∫ p d v = ?
M
1
1
p = p(v)
Wegabhängigkeit der Arbeit als
Prozessgröße
• isochore Zustandsänderung
→ z. B. ideale Flüssigkeiten mit ρ =
w v,12 = 0
mit
1
= const
v
dv = 0
• isotherme Zustandsänderung (ideales Gas)
p(v) = ?
→ p=
2
RT RT1 p1v1 p2 v 2 const
=
=
=
=
v
v
v
v
v
v
v
dv
= −RT1 ln 2 = −p1v1 ln 2
v
v1
v1
1
w v,12 = −const ∫
- Dissipative Arbeit
WWelle12 =
t 0 +Δt
∫
W
Welle ( t ) dt =
t = t0
t 0 +Δt
∫
Mdωdt = WR12 ≥ 0
t = t0
R
Wel12
=
t0 +Δt
∫
t = t0
( t ) dt =
W
el
t0 +Δt
∫
l2elReldt ≥ 0
t = t0
R
WR12 + Wel12
= Wdiss12 ≥ 0
δW = δWV + δWR + δWelR = δWV + δWdiss = ( dU)ad
δWges = δWV + δWdiss + δWä = ( dE )ad
3.2.4 Druckänderungsarbeit (Beispiel idealer Verdichter)
Arbeit für eine Arbeitsperiode AP
WAP = WV,12 + WV,23 + WV,34 + WV,41
2
3
4
1
1
2
3
4
= − ∫ pdV − ∫ pdV − ∫ pdV − ∫ pdV
2
= − ∫ pdV − p2 ( V3 − V2 ) − p1 ( V1 − V4 )
1
2
= − ∫ p ( V ) dV + p2 V2 − p1V1
1
2
w D,12 = ∫ v ( p ) dp
1
2
= ∫ V ( p ) dp = WD,12
1
3.2.5 Arbeit und innere Energie
v = const
−dEUmg = δWmech = −Mgdz = ( dU)ad = Mdu ( T,v ) = Mdu ( T )
Untersuchungen zum sogenannten „Mechanischen Wärmeäquivalent“ durch
James Prescott Joule (1818-1889) und Robert Mayer (1814-1878)
3.3
Der erste Hauptsatz
3.3.1 Formulierung mit der inneren Energie
− dEUmg = dESystem = d (Ekin + Epot + U) = δWä + δW + δQ
dU = δQ + δW
bzw.:
du = δq + δw
quasistatisch:
U2 − U1 = Q12 + W12
bzw.:
u2 − u1 = q12 + w12
du = δq − pdv + δ W R
2
u2 − u1 = q12 − ∫ p ( v ) dv + w R,12
1
3.3.2
Enthalpie
Definition:
H = U + pV = Mh
bzw. h = u + pv
dh = du + d(p ⋅ v ) = du + pdv + vdp
Ideales Gas:
(pv = RT)
dh = du + d(pv ) = c v (T )dT + R d T = dh(T )
⎛ ∂h ⎞
dh = ⎜ ⎟ dT = c p (T )dT
⎝ ∂T ⎠p
c p (T ) = c v (T ) + R
mit
ideale Flüssigkeit: dh = du + vdp = c (T )dT + vdp = dh(T, p )
(ρ = const)
⎛ ∂h ⎞
⎛ ∂h ⎞
dh = ⎜
dT
+
⎜ ⎟ dp
⎟
⎝ ∂T ⎠p
⎝ ∂p ⎠T
1. Hauptsatz:
(quasistationär)
mit
⎛ ∂h ⎞
1
v
=
=
⎜ ⎟
ρ
⎝ ∂p ⎠T
d h = δq + v d p + δw R
2
h 2 − h 1 = q1 2 +
∫ v (p ) d p + w
1
R ,1 2
3.3.3 Wärme bei reversiblen Zustandsänderungen
Voraussetzung: quasistatisch,
δw diss = 0
δqrev = du + pdv = dh − vdp
- reversibel isochor (dv = 0):
δqrev
⎛ ∂u ⎞
= du = cvdT + ⎜ ⎟ dv
⎝ ∂v ⎠T
0
mit
⎛ ∂u ⎞ ⎛ δq ⎞
cv = ⎜ ⎟ = ⎜ rev ⎟
⎝ ∂T ⎠v ⎝ dT ⎠v
- reversibel isobar (dp = 0):
Zustandsgl. allg.
δqrev
0
⎛ ∂h ⎞
= dh = cpdT + ⎜ ⎟ dp
mit
⎝ ∂p ⎠T
nur rev. isobar
- reversibel isotherm (dT = 0):
δqrev = ?
⎛ ∂h ⎞ ⎛ δq ⎞
cp = ⎜ ⎟ = ⎜ rev ⎟
⎝ ∂T ⎠p ⎝ dT ⎠p
3.3.4 Anwendung des 1. Hauptsatzes auf abgeschlossene Gesamtsysteme
Voraussetzung:
Δekin = 0, Δepot = 0, Vi = const
dUGS = ∑ dUi = δQ GS + δWGS = 0
⇒
i
Beispiel Kalorimeter:
∑ (Mc ) dT = 0
i
i
c i = const
∑ (Mc ) ( T
i
i2
− Ti1 ) = 0
Bestimmung von:
• spezifischer Wärmekapazität cProbe
• Mischtemperatur Ti2 = TM
• Mischungsverhältnis M1/M2
Zusammenfassung Arbeit
Zusammenfassung 1. Hauptsatz
3.4 Beispiele
Beispiel 3.1: Gasometer
Ein zylindrischer Gasbehälter (Gasometer) hat einen Durchmesser dG = 16 m und
eine Höhe zG = 20 m. Er wird durch einen vertikal verschiebbaren Deckel der
Masse MD = 50000 kg gasdicht abgeschlossen. Durch Sonneneinstrahlung
vergrößert sich das Gasvolumen. Der Deckel hebt sich um ΔzG = 0,5 m an. Das
Gas hat vor der Sonneneinstrahlung eine Temperatur von T1 = 293 K. Die
Gaskonstante, die spezifische Wärmekapazität und der Luftdruck betragen:
R = 287 J/(kgK), cp = 1004 J/(kgK) und pu = 105 Pa.
Berechnen Sie
a) die Gasmasse MG, die sich im
Gasometer befindet,
b) den Zustand T2, p2, V2 des Gases
nach der Sonneneinstrahlung,
c) die durch die Sonne zugeführte
Wärme Q12,
d) die Volumenänderungsarbeit WV12,
e) die Änderung der inneren Energie
ΔU = U2 – U1.
Lösungen
Beispiel 3.1: Gasometer
Der Deckel des Gasometers hat die Fläche A G = dG2 π / 4 = 201,06 m 2. Der
Absolutdruck p1 im Gasometer beträgt
MD g
= 0,10244MPa
AG
p1 = p u +
Die Behältervolumina vor und nach der Sonneneinstrahlung ergeben sich zu:
V1 = A G z G = 4021,2m 3
und
V2 = A G ( z G + Δz G ) = 4121,8 m 3 .
Die Gasmasse im Gasometer MG = V1ρ1 = V1p1 / (RT1 ) = 4898,7 kg bleibt
während der Zustandsänderung konstant. Die Zustandsänderung durch
Sonnenineinstrahlung vollzieht sich wegen des beweglichen Deckels isobar
p 2 = p1 = const. Somit folgt aus den thermischen Zustandsgleichungen
p1V1 = MGRT1
und
p 2 V2 = M GRT2
die Temperatur des Gases nach der Sonneneinstrahlung T2 = V2 / V1T1 = 300,3K.
Mit der Gleichung erhalten wir für die Volumenänderungsarbeit
2
W V12 = − ∫ pdV = − p1 ( V2 − V1 ) = −10,298 MJ.
1
Die durch die Sonne zugeführt Wärme Q12 lässt sich unmittelbar aus der
Enthalpieformulierungen des ersten Hauptsatzes berechnen.
Es ist
Q12 = H2 − H1 = MG c p ( T2 − T1 ) = 36,051 MJ.
Schließlich bestimmen wir noch die Änderung der inneren Energie mit dem ersten
Hauptsatz
U2 − U1 = Q12 + W V12 = 36,051 − 10,298 = 25,753MJ.