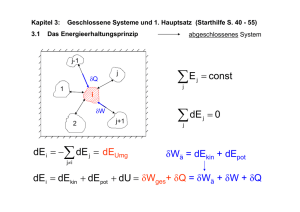
EinfidMet-II-3 - Meteorologisches Institut der Universität Bonn
Werbung

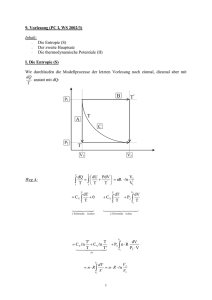
Einführung in die Meteorologie - Teil II: Meteorologische Elemente Clemens Simmer Meteorologisches Institut Rheinische Friedrich-Wilhelms Universität Bonn Sommersemester 2006 Wintersemester 2006/2007 II Meteorologische Elemente II.1 Luftdruck und Luftdichte II.2 Windgeschwindigkeit II.3 Temperatur II.4 Feuchte II.5 Strahlung II.3 Temperatur 1. Thermodynamische Systeme • thermodynamische Systeme • 0-ter Hauptsatz der Thermodynamik • Zustandsgrößen, Arbeit 2. 1. und 2. Hauptsatz der Thermodynamik • Carnot-Kreislauf 3. Potentiale und spezifische Wärme 4. Messskalen 5. Vertikalbewegungen • 6. 7. Potentielle Temperatur Fluss fühlbarer Wärme Temperaturmessung II.3.1 Thermodynamische Systeme Bei einem Luftvolumen interessiert uns meteorologisch nicht das einzelne Molekül und dessen Position und Bewegungszustand. Wir interessieren uns nur für deren relevante statistische Eigenschaften und die gegenseitigen Abhängigkeiten dieser statistischen Eigenschaften. Dies ist der Ansatz der statistischen Physik: Hier betrachten wird das Luftvolumen als ein sogenanntes thermodynamisches System. Thermodynamische Zustandsgrößen beschreiben ein thermodynamisches System z.B. p, T, V, n, innere Energie, …i.a. nicht unabhängig (siehe Gasgleichung) Gleichgewichtszustand p(t)=const, T(t)=const, …alle Zustandsgrößen sind zeitlich konstant Teilgleichgewichtszustand z.B. T(t)=const ↔ thermisches Gleichgewicht Was ist Temperatur? • Thermodynamik – Makro-Sicht, Masse+Volumen – Temperatur ist eine Zustandsgröße der Luft • die den Wärmeenergieinhalt (innere Energie) beschreibt, • die wichtig ist für die Richtung des Wärmetransports • Statistische Physik – Mikro-Sicht, Moleküle – Temperatur ist proportional zur mittleren kinetischen Energie der Moleküle (~v²) – Zeigt die Grenzen der Thermodynamik auf (Temperatur verliert ihren Sinn, wenn einzelne Moleküle betrachtet werden 0-ter Hauptsatz der Thermodynamik Die Temperatur kennzeichnet den Wärmezustand eines thermodynamischen Systems. Sind zwei Systeme miteinander in Kontakt, so ändert sich ihre Temperatur nur dann nicht, wenn diese gleich sind. Temperatur ist eine Zustandsgröße eines thermodynamischen Systems Im thermodynamischen Gleichgewicht ändert sich die Temperatur nicht Zustandsgrößen (a) Es sei der thermodynamische Zustand Beispiel ideales Gas (k=2): durch k Zustandsgrößen eindeutig T = T(p,V) = pV/(nR*) bestimmt. Eine weitere Größe T ist dann ebenfalls eine Zustandsgröße, p wenn gilt: T dT 0 T(p,V) entlang geschlossenem Weg V d.h. wenn bei einem beliebigen geschlossenen Weg des Systems im durch die k Zustandsgrößen aufgespannten Zustandsraum T wieder den gleichen Wert annimmt, oder wenn T eindeutig über die k Zustandsgrößen definiert ist. Zustandsgrößen (b) Alternativ ist die Feststellung, dass T genau dann eine Zustandsgröße ist, wenn sie sich als totales Differenzial von Zustandsgrößen darstellen lässt, die ein thermodynamisches System vollständig beschreiben. p → dp ds dV Beispiel: T = f(p,V) V T T T dT dp dV p T p V V T ds dp dV Achtung: Hier bezeichnen wir mit d nicht die Änderung eines mit dem Wind bewegten Volumens – eine Inkonsistenz im Bezeichnungssystem in der Meteorologie, leider. Auch der Nabla-Operator ist hier anders zu verstehen. Die Raumkoordinaten des Partikels sind ausgetauscht durch andere – allgemeinere – Koordinaten, die den Zustand eines Systems beschreiben. (Ausdehnungs)Arbeit eines Gases V → V + ΔV p ΔV = (Kraft/Fläche) x Volumen = Kraft x Weg = A (Arbeit) Dehnt sich ein Luftvolumen aus und verschiebt dabei angrenzende Luftvolumina gegen den dort herrschenden Druck, so leistet die Luft Arbeit an der Umgebung. Infinitesimal, d.h. sehr kleine Volumenänderungen (ΔV→0): A→δA=pdV Achtung: Wir benutzen δA anstatt dA, weil „d“ vollständigen Differentialen, d.h. Zustandsgrößen wie der Temperatur vorbehalten ist Übung zu II.3.1 1. Vollziehe mit unterem Diagramm das geschlossene Linienintegral der Ausdehnungsarbeit eines Gases nach: 2 3 4 1 1 2 3 4 A pdV pdV pdV pdV pdV A p (V A ? p p2 p1 2 2 V1 ) p1 (V2 V1 ) 0 also leistet das Gas Arbeit in 1 2 diesem " Kreisproze ss" A 0 , damit ist die Arbeit keine Zustandgröße 4 V1 3 VV eines idealen Gases 2 2. Schreibe mit Hilfe der Gasgleichung den Druck als vollständiges Differential von T und ρ; also dp=xdT+ydρ (bestimme x und y). II.3.2 Erster und zweiter Hauptsatz der Thermodynamik • • • • Ausdehnungsarbeit und Temperatur 1. Hauptsatz der Thermodynamik adiabatische Zustandsänderungen Carnot-Kreisprozess – Entropie – 2. Hauptsatz der Thermodynamik Quelle der Ausdehnungsarbeit und Auswirkung auf die Temperatur Bei fester Wand ändern auftreffende Luftmoleküle nur ihre Richtung; ihre kinetische Energie bleibt konstant und damit auch die Temperatur im Volumen. Bewegt sich die Wand z.B. durch den Druck der Luftmoleküle nach rechts, so haben die reflektierten Luftmoleküle eine geringere kinetische Energie; da die Temperatur proportional zur mittleren kinetischen Energie eines Luftmoleküls ist nimmt die Temperatur im Volumen ab. Ausdehnung eines Gases gegen einen äußeren Druck führt zur Abnahme der Temperatur des Gases. Die Temperatur hängt mit der inneren Energie des Gases zusammen. Es gibt also eine Umwandlung zwischen innerer Energie und Ausdehnungsarbeit (→ Erster Hauptsatz der Wärmelehre) 1. Hauptsatz der Thermodynamik 1. Führt man einem idealen Gas die Wärmemenge ΔQ zu, so kann das Gas diese in (Ausdehnungs-)Arbeit ΔA und innere Energie ΔU umwandeln: ΔQ = ΔA + ΔU 2. Die Ausdehnungsarbeit eines idealen Gases ist gegeben durch ΔA=p ΔV 3. Die innere Energie eines idealen Gases ist nur von der Temperatur abhängig U=U(T) 4. Wir führen spezifische Größen ein, also Q→q=Q/m, A→a=A/m, U→u=U/m mit m Masse du (T ) q pd oder dU (T ) Q pdV a A Bezeichnungen • Eine Zustandsänderung eines thermodynamischen Systems wird als adiabatisch bezeichnet, wenn keine Wärmezu- oder –abfuhr erfolgt, also δQ=0 oder δq=0 . • Erfolgt die Zustandsänderung ohne diese Einschränkung, so spricht man von diabatischen Zustandsänderungen. Beispiel Carnot-Kreislauf (a) dU (T ) Q pdV 1 2 isotherme Expansion (warm) dU (T ) 0 (da U nur von T abhängt) Q pdV 0 Q 0 Wärmezufuh r Isothermen (T=const) p 1 Q pdV PV nR*T 2 2 2 2 dV * * Q Q nR T nR Tw d ln V 12 w 1 V 1 1 4 3 V Adiabaten (kein Wärmeübergänge) nR *Tw dV V V2 nR Tw (ln V2 ln V1 ) nR Tw ln V1 * * Beispiel Carnot-Kreislauf (b) 2 3 adiabatisc he Expansion (großes V ) Q 0 (abgeschlo ssenes System) dU (T ) pdV dU (T ) Q pdV 0 dU 0 Temperatur abnahme Isothermen (T=const) p 1 Arbeitslei stung pdV des Systems auf Kosten der inneren Energie U 2 4 3 V Adiabaten (kein Wärmeübergänge) Einschub : Gleichvert eilungssat z (später genauer) n Mole des Gases f Freiheitsg rade eine Moleküls U (T ) 1 2 fnR*T , dU 12 fnR*dT pdV 1 2 Gasgleichung fnR*dT nR *T dV V 2 2 f dT dV 2 f , d ln T d ln V TkV3 TwV2 f 2 T V f Beispiel Carnot-Kreislauf (c) dU (T ) Q pdV 3 4 isotherme Kompressio n (kalt) dU (T ) 0 (da U nur von T abhängt) Q pdV 0 Q 0 Wärmeabfuh r Isothermen (T=const) p 1 nRTw dV V PV nRT Q pdV 2 4 4 dV * * Q Q nR T nR Tk d ln V 34 k 3 V 3 3 4 3 V Adiabaten (kein Wärmeübergänge) 4 nR *Tk ln V4 V3 Beispiel Carnot-Kreislauf (d) dU (T ) Q pdV 4 1 adiabatisc he Kompressio n (kleines V ) Q 0 (abgeschlo ssenes System) dU (T ) pdV 0 dU 0 Temperatur zunahme Isothermen (T=const) p 1 Arbeitslei stung pdV am System erhöht innere Energie U 2 2 TkV4 4 f TwV1 2 f 2 Adiabaten (keine Wärmeübergänge) 3 zusammen mit TkV3 V V2 V3 V1 V4 f TwV2 2 f folgt Carnot-Kreislauf dU (T ) Q pdV Isothermen (T=const) p 1 Folgerung 1 : dU (T ) 0 Q A 0 0 Q Q 12 2 Q34 0 zu zeigen als Übung d.h. dem System wird insgesamt 4 3 V Adiabaten (keine Wärmeübergänge) da U Zustandsv ariable Wärme zugeführt, womit es Arbeit leistet Carnot-Kreislauf Folgerung 2 : dU (T ) Q pdV Wirkungsgr ad der Wärmek raftmaschi ne geleistete Arbeit Isothermen (T=const) hinein gesteckte Wärme p 1 Q34 Q12 Q34 1 Q12 Q12 2 4 1 3 V Adiabaten (keine Wärmeübergänge) nRTk ln V2 nRTw ln V3 V1 V4 1 Tk Tw 1 , umso größer je größer die Temperatur differenz Carnot-Kreislauf dU (T ) Q pdV Isothermen (T=const) p 1 Q Q 12 Q T Q34 0 , aber Q12 Q34 0 Tw Tk Definition Entropie : S Q T 3 S ist eine Zustandsg röße Anmerkung : der Carnot - Kreislauf ist eine Idealisier ung (Annahme : thermische s Gleichgewi cht). Qirrev Es gilt : Carnot real 0 Übung T irreversibel V also dS 2 4 Adiabaten (keine Wärmeübergänge) Folgerung 3 : Definition der Entropie reversibel Q T In einem abgeschlos senen System (δQ 0) bleibt die Entropie konstant oder nimmt zu. Carnot-Kreislauf dU (T ) Q pdV Isothermen (T=const) p 1 2 4 Folgerung 4 : 2. Hauptsatz der Themodynam ik : Wärme kann nicht voll ständig in Arbeit umgesetzt werden. Folgerung 5 : Die Atmosphäre funktionie rt wie eine Wärmekraf tmaschine : Unter hohem Druck wird Wärme zugeführt (am Boden durch Wärm eflüsse), unter niedrigem Druck (oben, durch Ausstrahlu ng) wieder abgeführt. 3 V Adiabaten (keine Wärmeübergänge) Folgerung 6 : Neue Formulieru ng des 1.HS : du (T ) Tds pd Übungen zu II.3.2 1. 2. 3. Zeige, dass beim beschriebenen Carnot-Kreislauf (Folgerung 1) insgesamt Wärme zugefügt wird. Zeige, dass beim beschriebenen Carnot-Kreislauf das Linienintegral über δQ/T bei irreversiblen Prozessen nicht verschwindet (Folgerung 3) Versuche eine qualitative nur schematische Darstellung einer idealisierten Hadley-Zirkulation im p-V-Diagramm. Dabei fließt Luft am Boden von den Hochdruckgebieten der Subtropen zu der tropischen Tiefdruckrinne und erwärmt sich dabei durch Wärmeaufnahme vom Untergrund leicht. Dort steigt sie adiabatisch auf und fließt dann zurück unter leichter Druckabnahme und Temperaturabnahme (durch Abstrahlung in das Weltall) zu den Subtropen, wo sie wieder adiabatisch zum Boden sinkt. II.3.3 Thermodynamische Potentiale und spezifische Wärme • Bislang hatten wir den Zustand eines thermodynamischen Systems immer im pV-Diagramm dargestellt (siehe Carnot-Kreisprozess). • Im p-V- Diagramm können wir über die ideale Gasgleichung die Temperatur T eines idealen Gases eindeutig darstellen (Isothermen im p-V-Diagramm). • Der 1. Hauptsatz als totales Differential du=Tds-pdα gibt uns eine andere Möglichkeit der 2-dimensionalen Zustandsdarstellung eines thermodynamischen Systems, nämlich die innere Energie im s-α-Raum. • Eine energetische Zustandsdarstellung (u hat die Einheit einer spezifischen Energie, J/kg) wird bevorzugt, weil dann der Satz der Energieerhaltung unmittelbar anwendbar ist (z.B. Änderungen müssen durch Zu-/Abfuhr anderer Energien bewirkt werden. • Energetische Zustandsvariable werden auch als thermodynamische Potentiale bezeichnet. Mit du Tds pdα also u u(s, α) 1. T können folgende Beziehunge n abgeleitet werden : u u u u , p da du vollständi ges Diff. bzw. Definition part. Ableit. s α s α s α 2u 2u T 2. sα αs α s p sogenannte thermodyna mische Relationen s α Weitere thermodynamische Potentiale Die innere Energie ist offensichtlich eine adäquate Beschreibung eines thermodynamischen Systems, wenn man seinen Zustand in Abhängigkeit von der Entropie s und seinem spezifisches Volumen α betrachtet. Oft sind andere Darstellungen zweckmäßig, z.B. im T-α-Raum; dies erhält man durch Anwendung der sog. Legendre-Transformation. Ersetze s durch T durch Definition der freien Energie f u - Ts df d (u Ts ) du d (Ts ) Tds pd Tds sdT pd sdT f f (T , ) Analog erhalten wir für p Enthalpie h(s, p) und s T p freie Enthalpie g(T,p), also insgesamt : Innere Energie : u(s, ) du Tds pd Enthalpie : Freie Energie : h(s, p ) u p f (T , ) u Ts dh Tds dp df sdT pd Freie Enthalpie : g (T , p ) u Ts p dg sdT dp Damit haben wir drei weiter thermodynamische Potentiale, die zur Behandlung thermodynamischer Probleme verwendet werden können. Wenn wir z.B. den Sättigungsdampfdruck des Wasserdampfes, der nur von der Temperatur abhängt behandeln (e*=e*(T)), werden wir die freie Enthapie verwenden. Spezifische Wärmen c ≡ Wärmeenergiezufuhr pro Massen- und Temperatureinheit, [c]=J/(kg K) i.a. vom Weg, z.B. bei Gasen von Annahmen über p und α abhängig spezifisch e Wärme bei konstantem Volumen cv cv q dT Tds du dT dT du dT da du Tds-pdα und u u (T ) spezifisch e Wärme bei konstantem Druck c p cp q dT p Tds dh dT p dT p dh dT Joule-Kelvin-Prozess Vakuum u (T 0) 0 u cvT h(T 0) 0 h c pT da dh Tds αdp und h h(T ) T bleibt konstant Beziehung zwischen cv und cp Tds du pd cv dT d ( p ) dp mittels Gasgleichu ng cv dT RdT dp (cv R )dT dp dh dp wegen 1. H.S. dh Tds αdp c p dT dp c p cv R Luft : c p 1004 J/(kgK) cp cv 717 J/(kgK) f Anzahl der Freiheitsg rade RL 287 J/(kgK) (Nachweis übernächst e Seite) 2 2 1 1 1,4 cv f 5 Freiheitsgrade = unabhängige Bewegungsmöglichkeiten eines Teilchens, mit denen es innere Energie speichern kann Jedes Molekül besitzt drei Translationsfreiheitsgrade entsprechend den drei Raumrichtungen, in die es sich bewegen kann. Zweiatomige Moleküle besitzen zusätzlich zwei Rotationsfreiheitsgrade mit Achsen senkrecht zur Verbindungsachse Dreiatomige nichtlineare Moleküle besitzen drei Rotationsfreiheitsgrade Hinzu kommen Vibrationsfreiheitsgrade; einer beim zweiatomigen Molekül, drei bei einem dreiatomigen Molekül. Diese sind aber bei den Atmosphärentemperaturen wenig „aktiviert“. Da Luft i. W. aus 2-atomigen Molekülen besteht hat sie 5 Freiheitsgrade. Beweis von cp 2 1 cv f Gleichvert eilungssatz : Pro Freiheitsg rad beträgt die Energie eines Moleküls E 1 k BT mit k B 1,3806 10- 23 J/K Boltzmann - Konstante 2 Dann folgt * f f R E k T T 2 B 2 L dEmol f R *dT 2 * f R de du dT 2 M * f du R cv , dT 2 M , J / Molekül mit L Loschmidts che Zahl , J / Mol , J / kg mit M Molmasse * R c p cv * R M 1 f c p 1 f M 2 cv 2 Übungen zu II.3.3 1. 2. Leite die Formulierungen des 1. Hauptsatzes für Enthalpie und freie Enthalpie ab. Bestimme cp und cv für Luft unter der Annahme, dass diese nur aus Wasserdampf besteht. II.3.4 Definition der Temperatur und ihrer Maßskalen • • • • • 0-ter Hauptsatz Gasthermometer (über Gasgleichung) Gaskinetische Deutung 2. Hauptsatz der Thermodynamik Empirische Temperaturskalen (Celsius, Kelvin etc.) 0-ter Hauptsatz Temperatur ist eine Zustandsgröße. + Im thermischen Gleichgewicht haben alle Körper die gleiche Temperatur. Damit kann die Temperaturmessung erfolgen, in dem man einen Probekörper, dessen Temperatur man irgendwie messen kann, in den zu messenden Körper, z.B. die Luft, einbringen und so lange wartet, bis sich die Temperatur nicht mehr ändert. TP TK Prinzip des Gasthermometers Gasgleichu ng : pV nR T * 2 Zustände mit n const p,V,T und p0 ,V0 ,T0 nR* T V T p0 p V0 nR* T0 T0 p p0 i) p p0 const ii) V V0 const V T T0 V0 p T T0 p0 → Rechten Schenkel senken bis beide Flüssigkeitsspiegel auf gleicher Ebene sind. Dann ist Innendruck gleich dem äußerem Luftdruck. Dann kann die Volumenänderung (V) bestimmt werden und damit T. T0 → T0+ΔT T=T0 → Rechten Schenkel heben bis linker Flüssigkeitsspiegel wieder auf ursprünglicher Höhe ist. Dann ist V=V0. Dann kann die Druckänderung (p) über die Höhe der Säule bestimmt werden und damit T. Gaskinetische Deutung der Temperatur Ekin m 2 3 v k BT 2 2 mittlere kinetische Energie der Moleküle , T 0 v 0 2. Hauptsatz – Carnot-Kreisprozess q1 q2 q T 1 1 T1 T2 q2 T2 beim reversible m Kreisproze ss Stoff - unabhängig e Messung der Temperatur durch Bestimmung der Wärmeflüss e. Empirische Temperaturskalen Celsius - Skala : 0C 273,15 K Fahrenheit Skala : 0 F -17 ,78C , 100 F 37C (Körpertem peratur des Menschen) F 9 5 C 32 , C 5 9 F 32 Reaumur Skala : 0C 0 R , 100C 80 R Übungen zu II.3.4 • Um wieviel % seines Volumens dehnt sich ein Luftvolumen aus, wenn es isobar von 0°C auf 27°C erwärmt wird? • Wie schnell ist im Mittel ein Sauerstoffmolekül, wenn die Lufttemperatur 20°C beträgt? II.3.5 Temperaturänderung der Luft bei Vertikalbewegungen • • • • • • • Adiabatische Form des 1. HS der Thermodynamik Poisson-Gleichung Potentielle Temperatur Temperaturprofil in der turbulenten Grenzschicht Adiabatischer Temperaturgradient Energiebetrachtung beim Aufsteigen Potentielle Temperatur und Entropie Problemstellung Wir betrachten die Temperaturänderung eines Luftvolumens, das wir in der Atmosphäre (Umgebungu) nach oben oder unten verschieben. Annahmen: 1. „trocken“: keine Kondensation von Wasserdampf 2. adiabatisch: keine Wärmeleitung, Strahlungserwärmung oder Strahlungsabkühlung, oder Diffusion, also δq=0 3. Instantaner Druckausgleich mit der Umgebung, p=pu du(T ) pd 1. HS für adiabatische Prozesse : Ausgle ich zwischen Innerer Energie und Ausdehnun gsarbeit 4. Beim Aufsteigen nimmt nach der statischen Grundgleichung dpu=-ρugdz der Druck in der Umgebung (und im Luftvolumen p) ab. 5. Nimmt dabei die Dichte ab (und damit α zu), so leistet das Gas Ausdehnungsarbeit auf Kosten der inneren Energie u: diese (und mit u=cvT auch die Temperatur T) nehmen ab. Tu(z) aktuelles Temperaturprofil z T T T dT ? dz T T T zunächst: Temperaturänderung mit dem Druck - Poisson-Gleichung adiabatisc h q dh dp c pdT dp 0 RLT dp p mit dh c pdT und RLT Poisson Gleichung p mit Variablen trennung dT dp RL , c pd lnT RLd ln p mit Integratio n T p R T R p lnT2 lnT1 L ln p2 ln p1 , ln 2 L ln 2 mit exp() cp T1 c p p1 cp 0 T 0 -pk k StüweDiagramm 300 500 dT dp 1000 p T2 p2 c p T1 p1 RL k 0,286 cp p T ( p ) T ( p0 ) p0 TrockenAdiabaten -p RL T p 0 1000 T Definition der Potentiellen Temperatur θ = Temperatur, die ein Luftvolumen annimmt, wenn es adiabatisch auf einen Referenzdruck po (meist 1000 hPa) gebracht wird. Berechnung : Setze in Poisson - Gleichung p2 p0 Referenzdr uck -p 0 pA A T2 pB Referenzdr uck p1,T1 p,T beliebig B p0 TA θA TB Temperatur bei θB T p T 0 p RL cp Die potentielle Temperatur ist eine Konstante (konservative Größe) bei adiabatischen Bewegungen eines Luftvolumens. Adiabatischer Temperaturgradient c pdT dp ad 1.HS für adiabatische Bewegung (mit Enthalpie) z 1 u gdz mit dp pu u gz u gdz instantane r Druckausgl eich mit Umgebung dT dz dT dz Tu z ad RLT pu T gdz gdz wieder mit p pu p RLTu Tu T dT dz ad T g Tu c p g cp 0,98 K/100m Tu z T 1 Tu g cp T 1 Tu T T Temperaturprofil bei Durchmischung a) Atmosphäre sei in Ruhe. Sie werde vom Boden (bei T0) durch Wärmeleitung etc. angeheizt. Strahlungsprozesse in der Atmosphäre seien vernachlässigbar. b) Einsetzen von Turbulenz und damit vertikale Durchmischung, die innerhalb der Atmosphäre adiabatisch erfolgen soll. z z T0 T T(z)=T0=const im thermischen Gleichgewicht T0 T Adiabatisches Profil stellt sich ein mit T0 als Temperatur in Bodennähe. Energiebetrachtungen beim Aufsteigen c p dTad dp gdz Integratio n c p T T0 g ( z z0 ) 0 c pT0 c pT g ( z z0 ) wähle z0 als Referenzhö he c p c pT g ( z z0 ) const Enthalpie potentiell eEnergie Beim adiabatischen Aufstieg/Abstieg wird Enthalpie in potentielle Energie umgewandelt und umgekehrt. Aus der 1. Form des 1. HS mit der inneren Energie u folgte, dass bei adiabatischen Bewegungen innere Energie in Ausdehnungsarbeit umgewandelt wird bzw. umgekehrt. cpθ - und damit auch die potentielle Temperatur θ - sind Konstanten (konservative Größen) bei adiabatischen Umlagerungen. Entropie s und potentielle Temperatur θ q c p dT dp q dT 1 ds c p dp T T T ds c p d ln T RL d ln p ds c p d ln RL p0 c p T p p ln ln T RL ln cp p 0 c p ln c p ln T RL ln p RL ln p0 const c pd ln c p d ln T RLd ln p T q Tds c pTd ln c p d c p d ~1 Wärmezu und –abnahmen sind in etwa proportional zur Änderung der potentiellen Temperatur – und nicht der thermodynamischen Temperatur!!! Übungen zu II.3.5 1. 2. 3. 4. Zeige dass bei adiabtischen Zustandsänderungen gilt dT/dp|p=0 =∞. Ein Teilchen habe bei 500 hPa die Temperatur – 20°C. Welche Temperatur hätte es bei adiabatischer Bewegung auf 1000 hPa? Wie ändert sich in einer isotherm geschichteten Atmosphäre die potentielle Temperatur mit der Höhe? In 800 hPa habe ein Luftvolumen von 1 kg Masse die Temperatur 0°C. Es sinke adiabatisch auf 1000 hPa ab. Dort erhöhe sich danach seine Temperatur isobar um 5 K. Welche Temperatur und welche potentielle Temperatur hat dann das Teilchen? Um wie viel haben sich seine vier massenspezifischen thermodynamischen Potentiale geändert? II.3.6 Fluss fühlbarer Wärme • Die Atmosphäre wird wesentlich durch ihren Kontakt mit der Erdoberfläche erwärmt. • Direkt an der Erdoberfläche (wenige mm) geschieht das durch Wärmediffusion. Diese lässt sich wegen der Inhomogenität des Untergrundes nicht messen. • Oberhalb dieser sehr dünnen Schicht erfolgt der Wärmetransport i.w. durch Turbulenz; dieser Transport lässt sich, wie im letzten Kapitel diskutiert, durch hochfrequente Messung von Temperatur und Vertikalgeschwindigkeit direkt messen (oder aus dem Temperatur- und Windprofil abschätzen). • w‘T‘ ist nicht die geeignete Formulierung für den Wärmetransport, da sich T durch adiabatische Druckänderung mit der Höhe verändert, ohne dass Wärme transportiert wird. • w‘θ‘ ist die geeignete Formulierung, da die potentielle Temperatur eine Konstante bei adiabtischen Abläufen ist. Wärmehaushaltsgleichung - Vereinfachung durch potentielle Temperatur dh c pdT Tds dp Än derung der Enthalpie im Volumenel ement 1.HS dh cp dt dT ds dp T Änderun g mit der Zeit dt dt dt T v T t h T ds dp cp cp v T T Haushaltsg leichung der Enthalpie t t dt dt Adv ektion in das Volumen Quellen Senken im Volumen Vereinfach ung durch potentiell e Temperatur (Druckterm dann schon drin! ) d ds d c p d c pd ln ds , cp mit v dt dt dt t ds cp cp v t dt Adv ektion Qu Quellen und Senken ohne Druckterm Gemittelte Haushaltsgleichung (a) Mittelung von c p c p v Qu t cp cp v c p v t lokale Änderung der potentiell en Temperatur Adv ektion durch mittlere Strömung Qu Div ergenz des turbulente n Flusses v on c p gemittelter Quellterm Haushaltsg leichung der fühlbaren Wärme i ) Qu Erwärmung des Volumens durch innere Reibung Divergenz der Strahlungs flüsse H mol T c p aT Divergenz der molekulare nWärmeleit ung H mol mit Wärmelei tfähigkeit ( 0,026 J/(m 2s )) und a c p Temperatur leitfähigk eit ( 2 10 -5 m 2s ) T Annahme : 1 K / m H mol 0,026 W/m 2 x sehr klein! Gemittelte Haushaltsgleichung (b) cp cp v c p v t Adv ektion durch Div ergenz des lokale Änderung der potentiell en Temperatur mittlere Strömung turbulente n Flusses v on c p Qu gemittelter Quellterm ii ) c p v θ Advekti on fühlbarer Wärme (ist bei Divergenzf reiheit des Windfelde s proportion al zur Divergenz des konvektive n Transports fühlbarer Wärme H konv mit H konv c p v θ ii ) c p v θ der Divergenz des turbulente n Flusses fühlbarer Wärme Hturb c p v θ . Ist i.a. schwierig zu messen; daher werden Parametris ierungsans ätze entwickelt analog zu größerskal igen Flüssen. Gradientan satz : Hturb c p K mit K (i.a. a ) turbulente r Diffusions koeffizent H H mol Hturb Hturb in der freien Atmosphär e Turbulente Wärmeflüsse und vertikales Temperaturprofil A z B : A B keine Profilände rung, kein Wärme fluss A B TA nimmt zu, TB nimmt ab, Wärmeflus s nach unten A B TA nimmt ab, TB nimmt zu, Wärmeflus s nach oben 0 H 0 (kein Wärm efluss) z 0 H 0 (abwärts) z 0 H 0 (aufwärts) z z z z T,θ T,θ T,θ Übungen zu II.3.6 • Erläutere warum bei der Bestimmung des turbulenten Wärmeflusses (Fluss fühlbarer Wärme) H die potentielle Temperatur und nicht die Lufttemperatur verwendet werden muss. II.3.7 Temperaturmessung • Prinzipien: – Temperatur eines Probekörpers im thermischen Gleichgewicht (direkte Messung) – Strahlungsmessung und Interpretation nach Planckschem Strahlungsgesetz (Fernerkundung, Satelliten) – Laufzeitmessung des Schalls (Fernerkundung) • Meteorologisch wichtige Temperaturen: – Lufttemperatur (→Grundgleichungen) – Bodentemperatur (→Wärmeaustausch mit Untergrund) – Temperatur unter besonderen Bedingungen) • • • • Feuchtes Thermometer→Luftfeuchte Thermometer unter Sonnenbestrahlung→Sonnenstrahlung) Thermometer über kochendem Wasser→Luftdruck) Temperatur eines beheizten Drahtes→Windstärke) Direkte Messmethoden i) Flüssigkeitsthermometer: Prinzip: Ausdehnung von Flüssigkeiten bei Temperaturänderungen) ii) Bimetallthermometer: Prinzip: Unterschiedliche Ausdehnung zweier längs verlöteter Metallstäbe iii) Thermoelement: Prinzip: Verlöten zweier Metalle mit unterschiedlichen Austrittsarbeiten für Elektronen iv) Widerstandsthermometer: Prinzip: Widerstand R von Metallen und Halbleitern hängt von der Temperatur ab. Quecksilber (Hg) Schmelzpkt, °C Siedepkt., °C 96% Alkohol -38,8 -117 +359,7 +78 1 + 2 kleine große Austrittsarbeit ++ -- - + Tk Metalle : R R0 (1 ) Tw R T Halbleiter : R R0e b T R Flüssigkeitsthermometer • …sind (noch) meist verwendet in der Meteorologie • … benötigen wir jetzt um tieferen Verständnis der Temperaturmessung die Wärmehaushalts- und Oberflächenernergiebilanzgleichung • …daraus folgt die Notwendigkeit der Belüftung eines Thermometers. • …und die Bauart des Thermometers bestimmt die Trägheit (Ansprechzeit). • Alles gilt auch für die meisten anderen thermometerarten. Flüssigkeitsthermometer (1) Volumen : V ( ) V ( 0C )(1 w ) mit Temperatur in C Aufbau: w (Hg ) 18 10 5 K 1 TK nur 1 des Volumens bei T 50K 100 großer Flüssigkei tsbehälter mit sehr dünn ausgezogen em Schaft Wärmehaush altsgleich ung dU dT m c K , J/s W dt dt S F ab/zugefüh rteWärme über Oberfläche F durch Wärmeflus sdichte S, S W / m 2 U innere Energie der Flüssigkei t m Masse der Flüssigkei t c spezifische Wärmekapa zität der Flüssigkei t Trägheit des Thermomete rs : mc dTK S F dt hängt i.w. möglichst groß, damit schnelle möglichst Angleichun g klein an Luf ttemperatur also TL m, c klein F groß bei empf indlichen Thermomete rn nur v on T -Dif f erenz Thermomete r zu Luf t ab Flüssigkeitsthermometer (2) 4 mc dTK S Si F dt i 1 L TL TK turbulente r Fluss fühlbarer Wärme an die Umgebung mit L Wärmeüber gangskoeff izient KK kurzwellig e Strahlungs bilanz mit K kurzwellig es Absorptio nsvermögen TK und K einfallend e kurzwellig e Strahlungs flussdicht e TL TK (1-εK)K K α S(TW TK ) langwellig e Strahlungs bilanz TW mit S Strahlungs übergangsz ahl β TS TK und TW Umgebungst emperatur (z.B. Wand) Wärm eleitung aus dem Schaft mit Wärmeüber gangskoeff izient und TS Schafttemp eratur dTK Annahme : Stationari tät, d.h 0 dt 1 K K αS(TW TK ) β TS TK 0 TK TL L TK TS TK D.h. ist Tk konstant, so ist Tk nicht unbedingt die Lufttemperatur Tl , die ich messen will. Flüssigkeitsthermometer (3) Um TK TL (Thermomet er zeigt Lufttemper atur an), also TK TL 1 L K K αS(TW TK ) βTS TK 0 zu erreichen, können folgende Maßnahmen getroffen werden : 1) L muss möglichst groß sein v , v Anströmge schwindigk eit d d Durchmesse r des Thermomete rs sollte das Thermomete r belüftet werden Mit L 3 und/oder möglichst klein gehalten werden 2) Die Strahlungs terme können reduziert werden durch Strahlungs schutz und die Umgebung (Hütte) sollte auf Lufttemper atur gehalten werden 3) Der Schaft sollte ebenfalls möglichst auf Lufttemper atur gehalten werden (mit in Belüftung einbeziehe n) und möglichst dünn sein. Flüssigkeitsthermometer (4) - Zeitverhalten des idealen Thermometers dTK F F 1 mc S T T T T mit Trägheitsz eit L L K L K dt mc keine Strahlung, mc F L kein Wärmef luss ausSchaf t 1 Integratio n (Annahme TL const) : dTK 1 d lnTK TL dt TK TL ln TK TL 1 t t 0 TK ,0 TL TK TL TK ,0 TL e T Dif f erenz zur Zeit t t TK t0 exp t t 0 t0 T Dif f erenz zur Zeit t 0 Bei t t 0 e t t 0 TL e 1 0,368 1 / 3 also nach einer Zeitdauer von ist die ursprüngli che Temperatur differenz auf ein Drittel abgesunken 0,368TK ,0 TL t Übung: Bestimme die Reduktion in % von TK,0-TL nach einer Zeitperiode von 2, 4 und 6τ Übungen zu II.3.7 Bestimme die Reduktion in % der Anfangsdifferenz zwischen Thermometeranzeige und Lufttemperatur Tk,0TL nach einer Zeitperiode des zwei-, vier- und sechsfachen der Trägkeitszeit des Thermometers. Wie lange dauert es , bis man bei einem Thermometer mit Trägheitszeit 3 s bei einer Anfangsdifferenz von 10 K die Lufttemperatur mit einer Genauigkeit von 0,1 K bestimmen kann?