Document

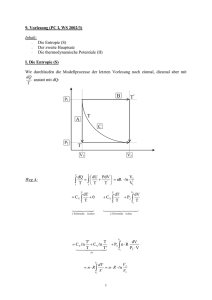
12. Vorlesung PCI
Inhalt:



Maxwell Relationen
Anmerkungen zur Gibbsenergie
Das chemische Potential:
I. Maxwell Relationen
Aus dem 1.Hauptsatz der Thermodynamik (dU=dQ+dW) folgt für reversible
Zustandsänderungen mit Hilfe des 2. Hauptsatzes dQrev =TdS. Daraus folgt: dU=TdSPdV.
Abgeleitet für reversible Prozesse, gilt diese Gleichung auch für andere Prozesse, da U eine
Zustandsfunktion ist. Sie heißt Fundamentalgleichung der Thermodynamik.
Der Koeffizientenvergleich des vollständigen Differentials
 U 
 U 
dU  
 dS  
 dV mit dU=TdSPdV
 S  V
 V S
liefert
 U 
T

 S  V
und
 U 
P
 .
 V  S
Der erste Ausdruck ist die thermodynamische Definition der Temperatur. Da der vorherige
Ausdruck ein vollständiges Differential ist, muss gelten:
2U
   U   !    U  
2U
 









VS V   S  V S S   V S  V SV
Daraus folgt dann
 T 
 P 

    .
 V S
 S  V
Dies ist eine der Maxwellrelationen, von denen es vier gibt und die durch analoges Vorgehen
ableitbar sind. Diese sind im einzelnen:
1
Für reversible Prozesse, vollständiges Differential in den
bzw. im Gleichgewicht natürlichen Variablen
gilt
Relationen durch
Koeffizientenvergleich
Maxwellrelationen
berechnet aus Relationen in
voriger Spalte (Reihenfolge
partieller Ableitungen ist beliebig)
dU= T dS  P dV
dU =  U  dS   U  dV
 U 
 U 
  P

  T und 
 V  S
 S  V
H 
 H 
dH = 
 dS  
 dP
dA=–PdV – S dT
 S  P
 P  S
dA =  A  dV   A  dT
 V  T
 T  V
 H 
 H 
 V

  T und 
 P  S
 S  P
 A 
A

   S und     P
 T  V
 V  T
dG= VdP – SdT
dG =  G  dP   G  dT
 G 
 G 

   S und 
 V
 T  P
 P  T
 T 
 P 

   
 V  S
 S  V
 T   V 
  

 P  S  S  P
 P 
 S 
  


T
  V  V  T
 V 
 S 

   
 T  P
 P  T
 S  V
dH= T dS + V dP
 P  T
 V S
 T  P
Nun wollen wir uns diese Tabelle, die Sie benutzen, jedoch nicht auswendig lernen sollten,
anwenden. Betrachten wir hierzu die Änderung der inneren Energie U bei isothermer
Volumenänderung: Definieren wir uns hierfür den Koeffizienten T als
 U 

  T
 V T
Das vollständige Differential
 U 
 U 
dU  
 dS  
 dV
 S  V
 V S
was wir uns oben hergeleitet haben, formen wir um zu:
 U   U   S   U   V 

 
 
 
 
 .
 V  T  S  V  V  T  V S  V  T
Mit Hilfe der Relationen in der Tabelle (siehe oben) ergibt sich daraus:
 U 
 S 

  T 
 P
 V  T
 V  T
Mit Hilfe der Maxwell-Relationen (Tabelle) läßt sich daraus die Entropie eliminieren:
 U 
 P 
T  
  T    P
 V  T
 T  V
Dies ist eine thermodynamische Zustandsgleichung. Das bedeutet, daß diese Gleichung
allgemein für jeden Stoff gültig ist! Sie gibt an, wie die Änderung der inneren Energie eines
Stoffes bei isothermer Volumenänderung mit der isochoren Druckänderung zusammenhängt.
Zur Veranschaulichung berechnen wir den Koeffizienten T für das ideale Gas und für das
Van-der-Waals-Gas.
2
Ideales Gas:
nR
 P 
T  T     P  T 
P  PP 0
V
 T  V
Van-der-Waals-Gas:
nRT
nR
n
 P 
P
 a     
V  nb  V 
 T  V V  nb
2
nR
nRT
a
 P 
n
n
T  T     P  T 

 a   a   2
V  nb V  nb  V 
Vm
 T  V
V
2
2
Man erkennt, dass beim Van-der-Waals-Gas der Koeffizient T den Binnendruck angibt.
II. Anmerkungen zur Gibbsenergie
Aus der Tabelle kann man die Temperaturabhängigkeit bei konstantem Druck als
 G 

  S entnehmen.
 T  P
Hinweis: für H=const folgt dieser Zusammenhang bereits aus der Definition G=H-ST.
Wichtig ist jedoch, daß die obige Relation immer gilt. Da S>0 ist, nimmt G mit steigender
Temperatur immer ab. Beim Vergleich von je 1 Mol fester, flüssiger, gasförmiger Materie
läßt sich schließen, daß die Änderung der freien Enthalpie des Gases mit der Temperatur
wesentlich stärker ist als für kondensierte Materie, da die Entropie des Gases am größten ist.
G
fest
flüssig
gasförmig
T
Bei einem Stoff liegen die drei Phasen nicht bei denselben Temperaturen vor, sondern wie im
unten dargestellten Diagramm:
G
P=const.
fest
flüssig
gasförmig
3
T
m
m
Tb
T
Die Druckabhängigkeit bei konstanter Temperatur lässt sich aus der Tabelle entnehmen als
 G 

 V
 P  T
Hinweis: Für U,V,S=const folgt dieser Zusammenhang bereits aus der Definition G=U+PVST. Wichtig ist jedoch, daß die obige Relation immer gilt.
Vergleichen wir nun die Aggregatzustände: Bei steigendem Druck nimmt die Gibbsenergie
der Gasphase nimmt am stärksten zu.
P1
G
P2>P1
fest
flüssig
gasförmig
Tm
Tm (P2)
T
Tb
Tb (P2)
Die Konsequenz aus diesem Diagramm ist, dass mit steigendem Druck der Siedepunkt zu
höherer Temperatur hin verschoben wird und der Schmelzpunkt wandert i.d.R. ebenfalls zu
höherer Temperatur. Hierfür gibt es jedoch Ausnahmen: Eine Ausnahme bildet Wasser. Sein
Volumen nimmt beim Gefrieren um ca. 8% zu! D.h. für Wasser nimmt die Gibbsenergie beim
Eis schneller zu als bei der Flüssigkeit  Gefrierpunkt sinkt mit steigendem Druck!
III. Das chemische Potential:
Nehmen wir an, in einem System liegen zwei verschiedene Stoffe oder sowohl eine flüssige
wie auch eine Gasphase vor: Dann verteilt sich die Gibbsenergie auf die Stoffmengen der
Teilchen beider Stoffe bzw. in den beiden Phasen; somit muß für eine energetische
Betrachtung die Gesamtenergie auf beide Phasen verteilt und sozusagen eine
stoffmengenabhängige Gibbsenergie, das chemische Potential eingeführt werden: Es ist rein
formal definiert als:
 G 


 n  P , T
Für einen reinen Stoff ist  identisch mit Gibbsenergie pro Mol, der molaren Gibbsenergie.
dG =  dn, bzw. G =   n
Für ein Gemisch von 2 Stoffen gilt:
4
G (P,T, n1,n2)
 G 
 G 
 G 
 G 


dG  
dP  
dT  
dn1  
dn 2


 P  T ,n1 ,n 2
 T  P ,n1 ,n 2
 n1  T ,P ,n 2
 n 2  T ,P ,n1
Für ein geschlossenes System (Zusammensetzung bleibt konstant, d.h. dn1=dn2=0) folgt:
dG = VdP – SdT.
Durch Koeffizientenvergleich erhalten wir:
 G 
V
und

 P  T ,n1 ,n 2
 G 
.
S  

 T  P ,n1 ,n 2
Durch die Anwendung der Definition des chemischen Potentials folgt:
 G 
 G 


1  
und  2  
.

n

n
 1  T ,P ,n 2
 2  T , P , n1
Damit erhalten wir:
dG=V dP  S dT + 1 dn1 + 2 dn2
Dies ist die Fundamental-Gleichung der Thermodynamik chemischer Prozesse.
Für konstanten Druck P und konstante Temperatur T ergibt sich
dG = 1dn1 + 2dn2.
Das chemische Potential gibt auch die Änderung der anderen thermodynamischen Potentiale
mit der Stoffmenge an:
 U 
 H 
 A 



i  
;  i  
; i  
 n i S,V,n ji
 n i S,P ,n ji
 n i  V,T ,n ji
5