thermodynamik genauer

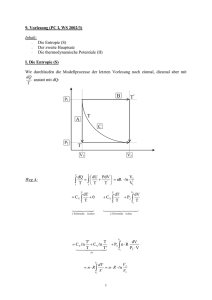
181
9. Wärmelehre
182
9.1 Temperaturskala
Temperatur T
Wärmeenergie:
Temperatur:
statistisch verteilte kinetische und potentielle
Energie in einem System
(relativ zum Grundzustand)
Maß für mittlere kinetische Energie eines
Systems (im Schwerpunktssystem)
Bemerkung: potentielle und kinetische Energie nehmen
mit der Temperatur zu; aber nur die kinetische Energie
ist streng proportional zur Temperatur
Definition:
Einheit Kelvin [K]
0K:
absoluter Nullpunkt
(keinerlei kinetische Energie
mehr im System)
273.16 K: Tripelpunkt des Wassers
(Eis, Wasser und Dampf sind
gleichzeitig vorhanden;
der Druck beträgt 612 Pa)
Damit ist die gesamte Temperaturskala festgelegt!
Es gilt:
Genauer:
Zwei Systeme in Kontakt tauschen Wärmeenergie
aus, bis sie im thermischen Gleichgewicht sind.
Ist System A mit System C und System B mit
System C im thermischen Gleichgewicht, so sind
auch A und B im thermischen Gleichgewicht.
„Nullter Hauptsatz der Thermodynamik“
Dient als theoretische Grundlage der Temperaturmessung
(System C kann als Thermometer verwendet werden)
Bemerkung: Die Kelvin-Skala entspricht der Celsius-Skala,
sie ist nur verschoben.
Die Celsius-Skala ist definiert über
0° C :
Schmelzpunkt des Wassers
bei 1.013 bar (273.15 K)
100° C : Siedepunkt des Wassers bei
1.013 bar (373.15 K)
183
9.2 Temperaturmessung: Thermometer
184
In molaren Einheiten:
Definition:
Ausnutzung thermischer Effekte:
Avogadro-Zahl NA (Zahl der Atome pro mol)
1 mol Atome 12C haben eine Masse von 12g
• Druck
⇒
NA = 6.022*1023 1/mol
• Materialausdehnung
• elektrischer Widerstand
Damit:
pV = Nk BT = N mol N A k BT = N mol RT
• thermoelektrische Spannung
R = NAkB = 8.31 J/Kmol
• Strahlungsleistung
• etc.
⇒ der Druck ist (bei festem Volumen) streng proportional
zur Temperatur:
9.2.1 Gasdruckthermometer
p=
Für ein ideales Gas gilt:
pV = Nk BT
Wird ausgenutzt beim Gasthermometer.
Klassischer Aufbau:
h
p Druck
V Volumen
N Anzahl Gasteilchen
(Atome oder Moleküle)
T Temperatur
kB : Boltzmann - Konstante
kB = 1.38 10-23 J/K
T
p0
T0
Höhe wird konstant
gehalten
Hg
Gas
Druck im Behälter:
flexible
Verbindung
p = pL + h ρ g
185
Bei der Eichtemperatur (z.B. 273.15 K):
186
l = l 0 (1 + α T )
Längenausdehnung:
p0 = pL + h0 ρ g
α: Ausdehnungskoeffizient
Bei einer anderen Temperatur ist dann:
p=
⇒
⇒
⇒
T
p0 = pL + h ρ g
T0
p − p0 = (
Werte:
T
− 1) p0 = (h − h0 ) ρ g
T0
ρ gT0
p0
α = 12*10-6 1/K
α = 0.51*10-6 1/K
V = V0 (1 + γ T )
Volumenausdehnung:
γ: Volumenausdehnungskoeffizient
T
ρg
−1 =
( h − h0 )
T0
p0
T=
Eisen
Quartz
Werte:
Benzol
γ = 10.6*10-4 1/K
Quecksilber γ = 1.8*10-4 1/K
( h − h0 ) + T0
Erlaubt präzise absolute Temperaturmessung!
9.2.2 Ausdehnungsthermometer
Die thermische Ausdehnung ist bei vielen Materialien
in breiten Temperaturbereichen proportional zur
Temperatur.
Gegenbeispiel: Wasser hat seine maximale Dichte bei 4°C
⇒
γ =0 bei T= 4°C
γ <0 bei 0<T< 4°C
γ <0 bei T>4°C
187
Kapillare
(Radius r)
Thermometer
∆x
Flüssigkeit
(Volumen V0)
188
9.3 Wärmekapazität
Gleichverteilungssatz:
im thermischen Gleichgewicht ist jeder Freiheitsgrad
eines Systems im zeitlichen Mittel mit der Energie
1
k BT
2
angeregt.
Eine geringe Veränderung des Volumens erzeugt eine
starke Verschiebung in der Kapillare
∆V = γ V0 ∆T = π r 2 ∆x
⇒
∆x =
V0
γ ∆T
πr2
(durch Wahl von Volumen und Kapillarradius läßt sich
die Verschiebung ∆x für eine gegebene Temperaturveränderung
beliebig groß machen!)
Freiheitsgrad:
jede verallgemeinerte Orts- und Impulsvariable
eines Systems, die quadratisch in die Gesamtenergie
eingeht (ausgenommen Schwerpunktskoordinaten)
Konkret: jede unabhängig wählbare kinetische Energie und
(bei Vibrationen) potentielle Energie bildet einen Freiheitsgrad
Die Temperatur ist dann also
π r2
∆T =
∆x
γ V0
Hier ist zu beachten, dass r und V0 ebenfalls von der
Temperatur abhängen, und dass der Ausdehnungskoeffizient
nur in einem beschränkten Temperaturbereich gültig ist.
Ein solches Thermometer muss daher an möglichst
vielen Temperaturfixpunkten geeicht werden.
Definition:
dQ
dT
Q: Wärmeenergie
1 dQ
M dT
M: Systemmasse
Wärmekapazität
C=
Spezifische Wärmekapazität:
c=
Genauer:
Wärmekapazität bei konstantem Volumen
CV
Wärmekapazität bei konstantem Druck
Cp
189
190
Bei „einfachen“ Systemen gilt:
ω
hier ist die kinetische Energie eines Moleküls:
m
1
1
C = f tot k B = N f k B
2
2
ftot : totale Zahl der Freiheitsgrade;
2-atomiges ideales Gas
Beispiel:
1
1
Q = f tot k BT = N f k BT
2
2
1 1 m
D
E kin = M v 2 + Jω 2 + rɺ 2 + r 2
2
2
4
2
m
f: Freiheitsgrade pro Atom
r
Rotation
Translation
Vibration
(kin. und pot. Energie)
1-atomiges ideales Gas
Beispiel:
m
v
1 E kin = m v 2
2
Freiheitsgrade:
pro Atom
1
1
1
2
2
2
= mv x + mv y + mv z
2
2
2
Atom
3 unabhängige Energien
⇒ 3 Freiheitsgrade (f=3)
f = 3
+
3
Eges = Q = N f
1
3
k BT = Nk BT
2
2
⇒
f = 3
+
2
CV =
3
Nk B
2
+
0 +
(die Rotation um die Molekülachse und die Vibration
werden nicht angeregt)
5
Eges = Q = N k BT
2
CV =
Wärmekapazität:
1 +
1 = 8
Aber: wegen quantenmechanischer Effekte sind Rotationen
mit kleinem Trägheitsmoment und Molekülvibrationen bei
Zimmertemperatur meist nicht angeregt
Die Gesamtenergie des Gases ist damit:
Gesamtenergie des Gases (mit N Atomen):
+
5
N k BT
2
0 = 5
191
Beispiel:
Festkörper
1 1 E = mv 2 + Dr 2
2
2
Energie pro Atom
m
⇒
f=
3
+
3 = 6
Gesamtenergie:
Q = 3 N k BT
Wärmekapazität
CV = 3N k B
192
Bemerkung: auch bei Festkörpern gilt: je tiefer die Temperatur,
desto weniger Vibrationsmoden sind angeregt
(nur solche mit etwa ℏ ω < k B T
)
Damit fällt cV für kleine T auf Null.
Wärmekapazität
verschiedener fester
Stoffe, aufgetragen gegen
die normierte Temperatur
T/TD
Dulong-Petit-Gesetz
Feste Stoffe haben also eine Wärmekapzität von
4.14 10-23 J/K pro Atom = 24.84 J/(K mol)
Die spezifische Wärmekapazität ist:
Die Debye-Temperatur TD hängt vom Material ab:
3N k B 3 N k B 3k B
cV =
=
=
M
NmAt mAt
Stoffe mit großen Atommassen haben geringe spezifische
Wärmekapazitäten!
Zahlenwerte
Material
mAt [u]
ρ [g/cm3]
cp [J/kgK]
C [J/K]1cm3
Messing
67.3
8.4
377
3.17
Aluminium
27.0
2.70
897
2.42
Blei
207.2
11.35
129
1.46
Alumunium
Kupfer
Zinn
Blei
TD = 426 K
TD = 345 K
TD = 195 K
TD = 96 K
193
9.3 Kinetische Gastheorie: Gasdruck
194
und damit den Druck:
p=
Fläche
A
Druck entsteht durch
Impulsübertrag bei
Stößen der Gasteilchen
mit der Wand
F 1
2 m
= nmv 2 = n v 2
A 3
3 2
2
2 3
N
= nE kin = n k BT = nk BT = k BT
3
3 2
V
Die Zustandsgleichung des idealen Gases lautet damit:
Gasgefülltes Volumen
pV = N k BT
Abschätzung der Zahl der Stöße mit der Wand
Annahme: alle Teilchen haben die gleiche Geschwindigkeit v
und bewegen sich nur in x-, y- oder z-Richtung
⇒ im Zeitraum ∆t treffen 1/6 der Teilchen im Volumen
v ∆t A auf die Fläche A
9.3.1 Boltzmann-Verteilung
Die Zahl der Stöße ist also
1
z = nv∆tA
6
Der Impulsübertrag dabei ist:
1
∆p = 2 zmv = nmv 2 A∆t
3
Die erzeugt eine Kraft:
F=
∆p 1
= nmv 2 A
∆t 3
Eine genauere Behandlung sollte die statistische Verteilung
der Geschwindigkeiten berücksichtigen.
n: Teilchendichte
n=
N At
V
Im thermischen Gleichgewicht ist die Wahrscheinlichkeit,
einen Zustand mit Energie E zu besetzen, gegeben durch
f ( E ) = a g e − E / kBT
BoltzmannVerteilung
g: Zahl der Zustände mit Energie E („Entartung“)
a: Normierungsfaktor
195
196
Die kinetische Energie für ein Gasteilchen ist:
Verteilung der
Geschwindigkeiten
der Moleküle
in Luft für verschiedene
Temperaturen
1 E = mv 2
2
Alle Geschwindigkeitsvektoren zu einer gegebenen Energie
bilden also eine Kugelschale im dreidimensionalen Geschwindigkeitsraum. Nimmt man an, dass jeder mögliche Vektor eine endliche Fläche
auf dieser Kugelschale ausfüllt, gibt es endlich viele mögliche
Vektoren, deren Zahl proportional zur Fläche der Kugelschale
(d.h. zu v2) ist. Es gilt hier also
g (v ) ∝ v 2
Diskussion:
Damit folgt für die Geschwindigkeitsverteilung in einem Gas:
Wahrscheinlichste Geschwindigkeit (Maximum von f(v) ):
2 m 
f (v ) =
π  k BT 
3/ 2
v2 e
m
− v 2 / kBT
2
Maxwell-Verteilung
vw =
Mittlere Geschwindigkeit:
∞
Die Normierungsfaktoren sind so gewählt, dass
2k BT
m
v = ∫ v f (v) dv =
8 k BT
π m
∞
0
0
Mittlere quadratische Geschwindigkeit:
∫ f (v)dv = 1
∞
v
2
= ∫ v f (v)dv =
0
3k BT
m
197
∞
Damit ist die mittlere kinetische Energie:
Ekin =
198
∫
Normierung:
f (vx ) dvx = 1
−∞
m 2
m 2
3k T
v =
v = B
2
2
2 m
Die mittlere quadratische Geschwindigkeit ist dann:
vx2 =
(3 Freiheitsgrade!)
∞
2
∫ vx f (vx )dvx =
−∞
f(v)
vw
<v>
<v2>
(auch negative
Werte möglich!)
MaxwellBoltzmannVerteilung
also
Ekin , x =
k BT
m
k T
m 2
vx = B
2
2
Zahl der Stöße auf Fläche A in Zeit ∆t :
∞
Z = ∫ nvx ∆tAf (vx )dvx
0
1
2
v/
0
3
2 kBT
(nur positive vx tragen bei!)
m
Impulsübertrag bei jedem Stoß:
∆ ps = 2mvx
9.3.2 Berechnung des Gasdrucks
v
v
v
x
v
vx
Für den Druck auf die Fläche A zählt
nur die Geschwindigkeitskomponente
senkrecht zu A (hier vx).
Gesamter Impulsübertrag in Zeit ∆t :
∞
∆ p = ∫ 2mvx nvx ∆tAf (vx )dvx
0
1D Geschwindigkeitsverteilung:
1
f (v x ) =
2π
m
m − 2 vx2 / kBT
e
k BT
∞
= 2n∆tAm ∫ v 2x f (vx )dvx
0
= n∆tAk BT
(1 Freiheitsgrad!)
199
Der Druck ist damit:
p=
∆p
N
= n k BT = k BT
∆ tA
V
In der Zeit ∆t ist dann die Energieerhöhung des Gases:
1
6
1
3
1
n
= n 3k BT ∆V = k BT ∆V = p∆V = ∆W
3
V
∆ E = Z ∆ ET = nv0 A∆t 2mv0 vK = n mv0 2 AvK ∆t
pV = N k B T
also
Auch bei expliziter Berücksichtigung der statistischen Verteilung der
Geschwindigkeiten erhält man das ideale Gasgesetz!
Gas
p
9.5 1. Hauptsatz
Geleistete Arbeit:
F
A
(unabhängig von der Kolbengeschwindigkeit vK!)
Die Erhöhung der inneren Energie des Gases (der kinetischen
Energie aller Gasteilchen) entspricht der geleisteten Arbeit!
9.4 Druckarbeit
∆x
200
∆W = F ∆ x = pA ∆ x = p ∆V
Für ein System, das an seine Umgebung nur durch Wärmübertrag
und Arbeit gekoppelt ist, gilt:
Führt zur Erwärmung des Gases!
∆U = ∆Q + ∆W
Kolben
Mikroskopische Beschreibung: betrachten ideales Gas,
Geschwindigkeit aller Gasteilchen v0, nur Richtungen x,y, oder z.
Während der Kompression bewege sich der Kolben mit
Geschwindigkeit vK; die Gasteilchen werden bei der Reflektion
beschleunigt:
v ' = v0 + 2 v K
vK
v0
∆ ET =
v‘
Dies führt zu einem Energiegewinn
pro auftreffendem Teilchen:
m 2 m 2 m 2
v ' − v0 = ( v0 + 4 v0 v K + 4 v K 2 − v0 2 )
2
2
2
≈ 2 mv0 v K
(für
v K ≪ v0 )
1. Hauptsatz der
Thermodynamik
(Energieerhaltung)
Zugeführte Wärme (Q) oder am System geleistete Arbeit (W)
erhöht die innere Energie (U) des Systems.
Andere Formulierung: es gibt kein perpetuum mobile, d.h. eine
Maschine, die Arbeit leistet, ohne Energie zu verbrauchen
(also ohne die innere Energie des Systems zu senken oder Wärme
zugeführt zu bekommen).
Falls nur Druckarbeit möglich ist:
dU = dQ − pdV
⇒
dQ = dU + pdV
201
202
Bemerkung: W bezeichnet die am System geleistete Arbeit
dV < 0 ⇒ dW = − pdV > 0
Volumenverkleinerung:
Mit
CV = N
f
kB :
2
Es wird Arbeit am System geleistet
Cp = N
dV > 0 ⇒ dW = − pdV < 0
Volumenvergrößerung:
f
f +2
k B + Nk B = N
kB
2
2
Isobare
Wärmekapazität
System leistet Arbeit
Hieraus ergibt sich das Verhältnis der beiden Wärmekapazitäten:
Beispiel: ideales Gas
U = CV T = N
Innere Energie:
Cp
f
k BT
2
CV
=
f +2
=γ
f
Adiabatenkoeffizient
dU = CV dT
f
dQ = dU + pdV = N k B dT + pdV
2
Damit:
9.5.2 Zustandsänderungen
Änderungen eines Systems können unter verschiedenen
Bedingungen stattfinden:
9.5.1 Isobare Wärmekapazität
Gas
p
F=konst.
A
dQ
Bei Zuführung der Wärmeenergie dQ
dehnt sich das Gas aus und leistet
Druckarbeit
⇒ geringere Temperaturerhöhung als
bei festem Volumen
pdV = n k B dT
⇒
dQ = dU + pdV = CV dT + Nk B dT = ( CV + Nk B ) dT
Cp =
dQ
dT
= CV + Nk B
p = konst .
T konstant
V konstant
p konstant
∆Q=0 (kein
Wärmeaustausch)
Für ideale Gase folgt:
Isothermer Fall
Bei konstantem Druck gilt:
⇒
• isotherm :
• isochor :
• isobar :
• adiabatisch :
dW
T
T konstant ⇒ U konstant (dU=0)
⇒
dQ = − dW = pdV
Endliche Volumenänderung:
dQ
T
Wärmebad
V
V
N
V
k BTdV = Nk BT ln
V
V0
V0
∆Q = ∫ pdV = ∫
V0
203
Vom System geleistete Arbeit:
204
Adiabatischer Fall
V
∆WS = − ∆W = ∆Q = Nk BT ln
V0
dW
Die auf das System übertragene Wärmeenergie wird vollständig
in Arbeit umgesetzt, die innere Energie ändert sich nicht.
kein Wärmeübertrag ⇒ dQ=0
dU = CV dT = dW = − pdV
Vom System geleistete Arbeit:
∆WS = −CV ∆T
Isolation
Isochorer Fall
Volumen konstant ⇒ dW=0
∆Q = ∆U = CV ∆T
⇒
V
Für die Änderung von der Temperatur in Abhängigkeit vom
Volumen folgt:
V
Übertragene Wärme wird vollständig
in innere Energie umgesetzt
(die Temperatur erhöht sich)
dQ
⇒
V0
Lösung:
Isobarer Fall
dQ = dU − dW = CV dT + pdV
dW
= C p dT
p
⇒
dQ
Damit gilt auch:
p
∆V
Nk B
∆WS = −∆W = p∆V = Nk B ∆T
∆Q = C p ∆T = C p
C
1
∆U = CV ∆T = V ∆Q = ∆Q
Cp
γ
Nk
∆WS = B ∆Q
Cp
Umsetzung der übertragenen Wärme
in innere Energie und Arbeit
∆U = CV ∆T = − ∫ p (V , T )dV
T V 
=
T0  V0 
−
2
f
Adiabatengleichung
pV
T
=
p0V0 T0
Andere Formulierungen durch Einsetzen
des idealen Gasgesetzes
p V 
=
p0  V0 
−
f +2
f
p T 
=
p0  T0 
V 
= 
 V0 
f +2
2
−γ
205
Beispiel: adiabatische Kompression kann zu starker
Temperaturerhöhung führen (hier für Luft)
V
1
=
V0 20
⇒
V 
T = T0  
 V0 
Druckerhöhung dabei:
−
2
5
= 300K *3.31 = 994K
V 
p = p0  
 V0 
−
7
5
206
9.6 Wärmekraftmaschinen
Wärmeenergie kann in mechanische Arbeit umgewndelt
werden; bei zyklischen Prozessen allerdings nicht mit
100% Wirkungsgrad!
9.6.1 Carnot-Prozess
= 66.3 bar
Beschreibt eine idealisierte Wärmekraft-Maschine.
Ein Zyklus besteht aus 4 Schritten:
1.
T1
vom System geleistete Arbeit:
9.5.2 Adiabatische Kompressibilität
Aus
 p
V = V0  
 p0 
−
Wärmebad 1
1
γ
1
− −1
Adiabatische Expansion V2 → V3
T1→T2
⇒
1 dV
1  1 V
= − − 
V dp
V γp
vom System geleistete Arbeit:
∆W2 = − ∆U = CV (T1 − T2 )
auf das System übertragene Wärme:
Damit ist die adiabatsiche Kompressibilität:
κ =−
V2
V1
∆Q1 = ∆W1
2.
dV
1 p
1 V
= V0 (− )
= (− )
1
−
dp
γ
γ p
p0 γ
∆W1 = Nk BT1 ln
auf das System übertragene Wärme:
∆W1
γ
folgt
Isotherme Expansion V1 → V2
T1
∆Q2 = 0
∆W2
3.
Isotherme Kompression V3 → V4
T2
vom System geleistete Arbeit:
T2
Wärmebad 2
1
κ=
γp
∆W3
∆W3 = Nk BT2 ln
V4
V3
(<0!)
auf das System übertragene Wärme:
∆Q3 = ∆W3
(<0!)
207
Adiabatische Kompression V4 → V1
4.
T2→T1
208
Der Wirkungsgrad (geleistete Arbeit durch zugeführte Wärme)
ist damit:
vom System geleistete Arbeit:
∆W4 = − ∆U = −CV (T1 − T2 )
η=
auf das System übertragene Wärme:
∆Q4 = 0
∆W4
Der Wirkungsgrad ist immer kleiner als 1 (und umso größer, je
größer das Verhältnis der Temperaturen der Wärmebäder T1/T2 ist)
Bei den adiabatischen Schritten gilt:
V3  T2 
=
V2  T1 
⇒
−
V2 V3
=
V1 V4
f
2
∆WS T1 − T2
T
=
=1− 2
∆Q1
T1
T1
und
V1  T1 
=
V4  T2 
bzw.
ln
−
f
2
V2
V
= − ln 4
V1
V3
Dieser für den Carnot-Prozess gefundene Wirkungsgrad
gilt allgemein; es gibt keinen Wärmekraftprozess, der einen
besseren Wirkungsgrad hat.
Schematisch:
Wärmebad 1
Es gilt:
Die vom System geleistete Arbeit ist also:
∆WS = ∆W1 + ∆W2 + ∆W3 + ∆W4
V
V
= Nk BT1 ln 2 + CV (T1 − T2 ) + Nk BT2 ln 4 − CV (T1 − T2 )
V1
V3
V2
= Nk B (T1 − T2 ) ln
V1
T1
Q1
Carnot-Prozeß
C
Q2
Die dem Wärmebad 1 entnommene Wärmeenergie ist:
V
∆Q1 = ∆W1 = Nk BT1 ln 2
V1
Q1 = W + Q2
T2
Wärmebad 2
W
W = η Q1
Die Wärmebad 1 entnommene
Wärme wird teilweise in Arbeit
umgewandelt und teilweise
Wärmebad 2 zugeführt.
209
Auftragung im pV-Diagramm
Der Stirling-Prozeß hat einen etwas schlechteren Wirkungsgrad,
weil bei der Verringerung der inneren Energie in Schritt 2 keine
Arbeit geleistet wird.
p
Carnot-Prozeß
V1
Adiabaten
p = p0V0γ
∆W
V2
T2
210
1
Vγ
Auftragung im pV-Diagramm
p
Stirling-Prozeß
1
Isothermen p = Nk BT
V
T1
T1
V4
V4
T2
V1
∆W
V
Isothermen
Fläche unter den Kurven:
∫ pdV
V2
(vom oder am Systen
geleistete Arbeit)
⇒ die im pV-Diagramm umlaufene Fläche ist die pro
Zyklus geleistete Arbeit ∆W
V
9.6.3 Kältemaschinen
9.6.2 Stirling-Motor
Die adiabatischen Schritte des Canot-Prozesses werden hier
durch eine einfache isochore Temperaturänderung des
Arbeitsmediums ersetzt.
Umkehrung des Vorgangs: es wird Arbeit am System geleistet,
und dabei Wärme aus dem unteren ins obere Wärmebad „gepumpt“.
T1
Damit ergeben sich die folgenden vier Schritte:
Q1 = W + Q2
Es gilt:
Q2 = Q1 − W =
Q1
1.
2.
3.
4.
Isotherme Expansion
Isochore Temperaturänderung
Isotherme Kompression
Isochore Temperaturänderung
W
Q2
⇒
T2
Q2 =
1
η
W −W
T2
W
T1 − T2
211
Je höher T1 und je niedriger T2, desto mehr Arbeit muß geleistet
werden, um eine bestimmte Wärmemenge aus Wärmebad 2 zu
entfernen.
Bemerkung:
Q1 ist immer größer als Q2 ! Ein offener Kühlschrank
(mit Wärmetauscher im selben Raum) kühlt daher nicht,
sonderen erwärmt den Raum.
212
S nimmt nach dem Zyklus wieder den gleichen Wert an!
Es handelt sich um eine Zustandsgröße (beschreibt den
Zustand eines Systems unabhängig davon, wie dieser erreicht
worden ist).
Entropie S
Definition:
dS =
Für diese gilt:
9.7 Entropie
Beim Carnot-Prozeß sind die pro Zyklus übertragenen Wärmen:
dQrev : bei einem reversiblen
V
∆Q1 = Nk BT1 ln 2
V1
Prozeß übertragene Wärme
9.7.1 Entropie ideales Gas
V
∆Q2 = − Nk BT2 ln 2
V1
Damit ist
aber
Für die Größe
Bei der isothermen Expansion gilt:
∆Q2 ≠ − ∆Q1
∆Q2
T2
=−
∆S =
∆Q1
T1
∆Q
T
dQrev
T
∆W = −∆Q = − Nk BT ln
bzw.
∆Q2
T2
+
∆Q1
T1
=0
⇒
∆S =
∆Q
T
= Nk B ln
V
V0
V
V0
Bei der isochoren Temperaturänderung gilt:
gilt also:
∆ S zykl = ∆ S1 + ∆ S 2 = 0
dQ = dU + pdV = dU = CV dT
⇒
dS =
dQ CV
=
dT
T
T
(am System
geleistete Arbeit)
213
214
T
also
CV
T
dT = CV ln
T
T0
T0
∆S = ∫
(falls CV konstant ist)
Einen beliebigen T,V-Zustand (womit auch p festgelegt ist) kann
man z.B. durch Änderung erst von V, dann von T erreichen.
Beispiel: isotherme Expansion eines idealen Gases
V1
V2
Wahrscheinlichkeit für ein Teilchen in V2, sich in einem
Teilvolumen mit Ausdehnung V1 aufzuhalten:
Damit ist die Entropie dieses neuen Zustands:
p=
S = S0 + CV ln
T
V
+ Nk B ln
T0
V0
Entropie des
idealen Gases
Wahrscheinlichkeit für N Teilchen, sich alle in V1 aufzuhalten:
9.7.2 Statistische Bedeutung der Entropie
Für die Entropie zweier Zustände eines Systems gilt:
S1
P
= Nk B ln 1
S2
P2
V1
V2
Pi: Wahrscheinlichkeit
des Zustands
(da ungeordnete Zustände häufig wahrscheinlicher sind als
geordnete, ist die Entropie auch ein Maß für die „Unordnung“)
Diese Definition erlaubt es, die Entropie durch Abzählung
der „Mikrozustände“ zu einem Zustand zu berechnen.
V 
P =  1 
 V2 
N
Ordnet man auch dem Zustand „alle Teilchen in V2“ eine
Wahrscheinlichkeit zu, erhält man:
N
V 
P1 =  1  P2
 V2 
Die Entropieänderung bei Volumenzunahme ist damit:
∆S = S 2 − S1 = k B ln PV2 − k B ln PV1
PV2
N
V
V
= k B ln
= k B ln( 2N ) = Nk B ln 2
PV1
V1
V1
Es ergibt sich das gleiche Ergebnis!
215
9.8 2. Hauptsatz
216
∆ S1 = −
Entropieänderung Wärmebad 1:
Bei spontanen Zustandsänderungen eines abgeschlossenen
Systems gilt:
∆S ≥ 0
2. Hauptsatz der
Thermodynamik
T1
∆Q2 1
Entropieänderung Wärmebad 2: ∆ S 2 =
= ( ∆Q1 − ∆W )
T2
T2
In der statistischen Betrachtung: ein System geht nicht von
selbst in einen unwahrscheinlicheren Zustand über!
(bis auf statistische Schwankungen, die zu geringen negativen
∆S führen können. Im thermodynamischen Limit, d.h. für
unendlich große Systeme, geht die relative Amplitude dieser
Schwankungen gegen Null).
Ein Vorgang ist reversibel, wenn er durch
infinitesimale Änderung eines Parameters
umgekehrt werden kann.
Definition:
irreversible Vorgänge
∆S > 0
η < ηCarnot
Bei
abgeschlossenes
System
T1
Q1
C
Q2
W
∆Q1 = ∆Q2 + ∆W
T2
wird
∆W = η∆Q1
Arbeit kann gespeichert
werden, z.B. durch adibatische
Kompression eines Gases
(∆Q=0 ⇒ ∆S=0 )
=
1
∆Q1
T1
∆Q2 > ∆Q2Carnot
∆ S 2 > − ∆ S1
fl
∆S > 0
Beispiel: Expansion eines Gases
adiabatische (reversible) Expansion
dW
Beispiel: Carnot-Prozeß
1
1 T 
(1 − η ) ∆Q1 =  2  ∆Q1
T2
T2  T1 
Der Carnot-Prozeß ist reversibel! Für einen Kraftwärmeprozeß
mit schlechterem Wirkungsgrad gilt dies nicht:
fl
∆S = 0
=
∆ S = ∆ S1 + ∆ S 2 = 0
Zusammen:
Für das Gesamtsystem gilt:
reversible Vorgänge
∆Q1
Gas
∆Q = 0
Schieber
(instantan geöffnet)
Gas
⇒ ∆S = 0
irreversible Expansion
ideales Gas:
∆ S = Nk B ln
V2
>0
V1
217
9.9 Einschub: Wärmetransport
Beispiel: Temperaturausgleich
System A
∆Q
T1
Entropieänderung System A:
Entropieänderung System B:
Zusammen:
218
System B
T1 > T2
T2
∆ S1 = −
∆S2 =
∆Q
Zwei Systeme unterschiedlicher Temperatur tauschen Wärme aus;
es wird immer mehr Wärme vom warmen auf das kalte System
übertragen als umgekehrt. Bei Temperaturgleichheit ist der
resultierende Wärmetransport Null.
Es gibt drei Arten von Wärmetransport:
T1
• Wärmeleitung
• Konvektion (in Gasen und Flüssigkeiten)
• Wärmestrahlung
∆Q
T2
1 1
− >0
T
 2 T1 
∆ S = ∆ S1 + ∆ S 2 = ∆Q 
9.9.1 Wärmeleitung
In Gasen, Flüssigkeiten und Festkörpern tauschen die Teilchen
durch Stöße (im Wesentlichen) kinetische Energie aus. In
wärmeren Bereichen haben die Teilchen höhere kinetische
Energien ⇒ Energie wird von wärmeren in kältere Bereiche
transportiert.
Irreversibler Vorgang!
Damit legt der zweite Hauptsatz die Richtung des
Wärmetransports fest: Wärme wird immer vom heißen zum
kalten System übertragen!
Beispiel: Gas bei geringem Druck
T1
3
Ekin = k BT1
2
T2
3
Ekin = k BT2
2
Annahme: die Gasteilchen
stoßen inelastisch mit den
Wänden und nehmen
deren Temperatur an
⇒ bei jedem Stoß auf die
rechte Wand wird die Energie
3
k B (T1 − T2 )
2
übertragen.
219
220
Jeder Stoß auf die linke Wand übeträgt die Energie
3
2
Zahlenwerte (0º C):
k B (T2 − T1 )
Gesamtwärmetransport:
3
Qɺ = Zɺ k ∆T
2 B
Material
λ [W/mK]
Ag
420
Pb
36
Quartz
1,4
Wasser
0,54
Luft
0,024
Zahl der Stöße pro Zeit
Gilt nur bei niedrigem Druck; bei höherem Druck finden Stöße
auch im Volumen statt; damit wird die pro Stoß auf die Wand
übertragene Energie geringer.
Bemerkung: dieses Gesetz läßt sich auf eine beliebige Temperaturverteilung erweitern. Der Wärmestrom in einem
isotropen Material ist gegeben durch
jth = −λ∇T
Im Festkörper und in Flüssigkeiten gibt es zwei Formen
der Wärmeleitung:
bei allen Stoffen:
bei leitenden Stoffen:
durch Atombewegung
durch Elektronenbewegung
Allgemein gilt für den Wärmetransport durch ein Volumen:
9.9.2 Konvektion
Strömung von Flüssigkeiten oder Gasen zwischen Bereichen
unterschiedlicher Temperatur, verursacht durch Wärmeausdehnung
und Schwerkraft.
Führt häufig zu sehr viel
stärkerem Wärmetransport
als reine Wärmeleitung.
l
T1
Gas, Flüssigkeit,
Feststoff
T2
Querschnittsfläche A
A
Qɺ = λ ∆T
l
λ: Wärmeleitkonstante
A: Querschnittsfläche
l: Länge
T1
T2
T1
T2
(hängt ab von Ausdehnungskoeffizienten, Wärmekapazität,
Dichte, Viskosität, Geometrie
fl nicht einfach zu beschreiben)
kaltes Medium wird aufgewärmt
und steigt auf
221
9.9.3 Wärmestrahlung
222
9.10 Alternative Formulierung 2. Hauptsatz
Jeder Körper strahlt Wärmestrahlung ab; die abgestrahlte
Leistung ist etwa:
„Es gibt keine periodisch arbeitende Maschine, die Arbeit
leistet und dabei nur ein Wärmebad abkühlt“
P = ε Aσ T 4
D.h. es gibt kein sogenanntes perpetuum mobile 2. Art.
ε : Emissivität (0 < ε <1)
A : Oberfläche
σ : Stefan-Boltzmann-Konstante
σ = 5.7 10-8 Wm-2K-4
Die Formel gilt exakt für den idealen schwarzen Körper (ε=1); bei
anderen Oberflächen wird ein wellenlängenunabhängiger Wert
von ε < 1 angenommen - dies ist aber eine Näherung.
P1
T2
T1
P2
Flächengröße A
(ein perpertuum mobile 1. Art ist eine Maschine, die Arbeit leistet,
ohne Energie aufzunehmen)
Zusammenhang mit der Aussage, dass die Entropie nur
zunehmen kann: gäbe es die oben beschriebene Maschine,
ließe sich damit die Entropie eines geschlossenen Systems
erniedrigen.
Beweis:
Von der Fläche 1 abgestrahlte
Leistung:
4
P1 = ε1 Aσ T1
Von der Fläche 2 aufgenommene
Leistung:
4
P12 = ε 2ε1 Aσ T1
Das perpertuum mobile 2. Art
ließe sich mit einem CarnotProzeß koppeln.
T1
Q1
Q‘1
P2
C
W
Q‘2
Analoges gilt für den Energietransport von 2 nach 1. Damit ist
die transportierte Leistung:
Genauer: berücksichtigt man, dass die nicht absorbierte Leistung
reflektiert wird, erhält man:
εε
1 2
ε1 + ε 2 − ε1ε 2
Aσ (T14 − T24 )
Q '1 = Q '2 + W = Q '2 + Q1
also
T2
P = ε1ε 2 Aσ (T14 − T24 )
P=
Carnot
Die in das obere Wärmebad
eingebrachte Wärme wäre dann:
Q '1 > Q1
Das obere Wärmebad würde
immer wärmer werden!
Entropieänderungen:
∆S2 = −
Q '2
1 T2
1
=−
W =−
Q1
T2
T2 T1 − T2
T1 − T2
223
∆ S1 = −
 1
Q1 Q '1
Q
1
1
+
=− 1+
W =
−  Q1
T1 T1
T1 T1 − T2
 T1 − T2 T1 
Zusammen:
∆ S = ∆ S1 + ∆ S 2 = −
Q1
<0
T1
dU ≤ d (TS ) − SdT − pdV
Q1 Q2  1 1 − η 
Q1 = 0
+
= − +
T1 T2  T1
T2 
Bei einem η >ηCarnot wäre also ∆ S < 0
∆S = −
9.11 Zustandsfunktionen
dU ≤ TdS − pdV
d (U − TS ) ≤ − SdT − pdV
F = U − TS
Für diese gilt offenbar:
Freie Energie
dF ≤ − SdT − pdV
(Gleichheit
bei reversiblen
Vorgängen!)
Die von einem System isotherm geleistete Arbeit ist:
Für beliebige Zustandsänderungen eines System gilt:
folgt damit:
⇒
Wir definieren eine neue Zustandsfunktion:
Bei dem Carnot-Prozeß ist wie schon gezeigt
dU = dQ + dW = dQ − pdV
d (TS ) = SdT + TdS
Eingesetzt in obige Gleichung:
„Es gibt keine Wärmekraftmaschine, die einen besseren
Wirkungsgrad hat als der Carnot-Prozeß“
Zusammen mit dem 1. Hauptsatz
Diese Aussage läßt sich mithilfe eine Koordinatentransformation
(Legendre-Transformation) neu formulieren.
1. Es gilt:
Alternative Formulierung:
dQ
dS ≥
T
224
(Gleichheit
bei reversiblen
Vorgängen!)
dWS = pdV ≤ − dF − SdT = − dF
=0
Die isotherm geleistete Arbeit ist also maximal die Abnahme der
freien Energie!
Im isotherm-isochoren Fall gilt:
dF ≤ − SdT − pdV = 0
Bei festem T,V kann sich die freie Energie nur verringern;
im Gleichgewicht nimmt F den kleinstmöglichen Wert an.
225
d ( pV ) = pdV + Vdp
2. Es gilt:
226
3. Setzt man
d (TS ) = SdT + TdS
Eingesetzt in obige Gleichung:
dU ≤ TdS − d ( pV ) + Vdp
⇒
in obige Gleichung ein, ergibt sich:
d (U + pV ) ≤ TdS + Vdp
dU ≤ d (TS ) − SdT − d ( pV ) + Vdp
⇒
Wir definieren die Zustandsfunktion:
H = U + pV
Für diese gilt:
d ( pV ) = pdV + Vdp
Wir definieren die Zustandsfunktion:
Enthalpie
dH ≤ TdS + Vdp
d (U − TS + pV ) ≤ − SdT + Vdp
G = U − TS + pV
(Gleichheit
bei reversiblen
Vorgängen!)
Im isentropen-isochoren Fall gilt:
dH ≤ TdS + Vdp = 0
Für diese gilt:
dG ≤ − SdT + Vdp
Freie Enthalpie
(Gleichheit
bei reversiblen
Vorgängen!)
Im isotherm-isochoren Fall gilt:
Bei festem S,V kann sich die Enthalpie nur verringern und nimmt
im Gleichgewicht den kleinstmöglichen Wert an.
dG ≤ 0
G wird im Gleichgewicht minimal.
Bemerkung: die Enthalpie wird in der Chemie häufig verwendet,
da viele Prozesse isobar ablaufen.
Z.B. gilt bei dem isobaren, reversiblen Verdampfen einer
Substanz:
dH = TdS + Vdp = TdS = dQ
Die Verdampfungsemthalpie ist also einfach die für das
Verdampfen (einer bestimmten Stoffmenge) benötigte Wärme.
Bemerkung:
Es gilt immer
Aber nur im einfachsten Fall ist
dU = dQ + dW
dW = − pdV
Es sind weitere Formen von Arbeit möglich, mit denen
das System an die Umgebung koppeln kann.
227
z.B.:
Zusammenfassung
dW = −σ dA
Arbeit gegen die
Oberflächenspannung
dW = HdM
Änderung der Magnetisierung
im magnetischen Feld
dW = µ dN
Änderung der Teilchenzahl
(µ: chemisches Potential)
etc.
Hierbei gilt immer: die Arbeit ist das Produkt einer intensiven
und einer extensiven Größe.
intensiv:
extensiv:
unabhängig von der Systemgröße (T, p, µ)
proportional zur Systemgröße (S, V, N)
Damit gilt bei variabler Teilchenzahl:
dU = dQ − pdV + µ dN
Und bei reversiblen Vorgängen:
dG = − SdT + Vdp + µ dN
Isotherm-isochor:
228
dG = µ dN
Die freie Enthalpie entspricht also dem chemischen Potential
aller Teilchen (für T,p konstant).
Bei reversiblen Zustandsänderungen gilt („einfache Systeme“):
1
dQ
T
dU = TdS − pdV
Entropie
dF = d (T − US ) = − SdT − pdV
Freie Energie
dH = d (U + pV ) = TdS + Vdp
Enthalpie
dG = d (U − TS + pV ) = − SdT + Vdp
Freie Enthalpie
dS =
Damit gilt auch:
 ∂F 
 ∂G 
S = −
 = −

 ∂T V
 ∂T  p
 ∂U 
 ∂F 
p = −
 = −

 ∂V  S
 ∂V T
 ∂H 
 ∂G 
V = −
= −


 ∂p  S
 ∂p T
Innere Energie
229
9.13 Reale Gase
9.12 3. Hauptsatz
Bisher wurde Entropie nur relativ definiert. Der dritte Hauptsatz
legt den absoluten Wert fest.
T →0
Reale Gase zeigen eine Abweichung vom idealen Verhalten
wegen der Wechselwirkung der Gasteilchen untereinander.
Näherungsweise lassen sie sich beschreiben durch die
Van-der-Waals-Gleichung:
Für reine, kristalline Stoffe gilt:
lim S (T ) = 0
230
3. Hauptsatz
der Thermodynamik
N2
( p + a 2 )(V − Nb) = Nk BT
V
„Binnendruck“
„Kovolumen“
(bei T=0K gibt es keine „Unordnung“ mehr)
Daraus folgt direkt: T = 0K ist nicht erreichbar!
Abkühlung ist nur möglich durch den Kontakt mit einem Wärmebad
oder durch adiabatische Prozesse.
In erstem Fall wird die (endliche) Temperatur des Wärmebads
angenommen (worraus ein endlicher Wert für die Entropie
folgt), in zweitem kann die Entropie nur gleich bleiben, aber
nicht verkleinert werden. Damit ist S=0 nicht erreichbar, und folglich
auch T=0K nicht.
Der Binnendruck ensteht durch die Anziehung der Teilchen
untereinander (van-der-Waals-Wechselwirkung) und erhöht
die Kompression des Gases. Das Kovolumen beschreibt die
endliche Ausdehnung der Teilchen, aufgrund derer das
Gas nicht beliebig dicht zusammengepresst werden kann.
Aufgelöst nach dem Druck:
Nk BT a N 2
p=
−
V − Nb V 2
Kritischer Punkt
Flüssigkeit
Phasengemisch
Gas
231
Für die innere Energie eines van-der-Waals-Gases gilt:
232
f
N2
U = N k BT − a
2
V
gilt dann:
∂H
dT
= − ∂V
∂H
dV
∂T
Die innere Energie ist volumenabhängig! Dies führt zu
Temperaturänderungen bei der Expansion.
⇒
9.13.1 Joule-Thomson-Effekt
„Entspannung“ (Expansion) eines realen Gases.
F1
F2
An einem strömenden
Gasvolumen V1 wird die
Arbeit geleistet:
p1V1
p1
p2
Düse oder
poröse Wand
Es leistet die Arbeit:
Für das van-der-Waals-Gas also:
f
N 2  Nk BT
N2 
H = N k BT − a
+
− a 2 V
2
V  V − Nb
V 
p2V2
Die Differenz muss die innere
Energie verändern:
⇒
U1 + p1V = U 2 + p2V2
V 
N2
f
= Nk BT  −
 − 2a
V
 2 V − Nb 
Damit:
H1 = H 2
Die Enthalpie bleibt erhalten! Anders ausgedrückt:
dH = 0
Temperaturänderung
bei isenthalper
Volumenänderung
H = U + pV
Es ist
U 2 − U1 = p1V1 − p2V2
Umgeformt:
∂H
∂H
dV +
dT
∂V
∂T
∂H
∂H
dV = −
dT
∂V
∂T
dH =
Mit
− Nb
N2
∂H
Nk BT
+ 2a 2
2
dT
V
Nb
V
(
)
−
= − ∂V = −
∂H
V 
dV
f
Nk B  −

∂T
 2 V − Nb 
233
Mit
Nb ≪ V
wird dies:
dT NbT − 2aN / k B
=
dV
f
 2
 − 1V
2 
Für große Temperaturen ist der Zähler positiv; die Temperatur
nimmt bei Volumenvergrößerung zu. Bei kleinen Temperaturen
ist der Zähler negativ; die Temperatur nimmt ab.
Die Grenze zwischen beiden Bereichen ist die Temperatur:
Ti =
2a
kBb
Inversionstemperatur