Physikalische Thermodynamik

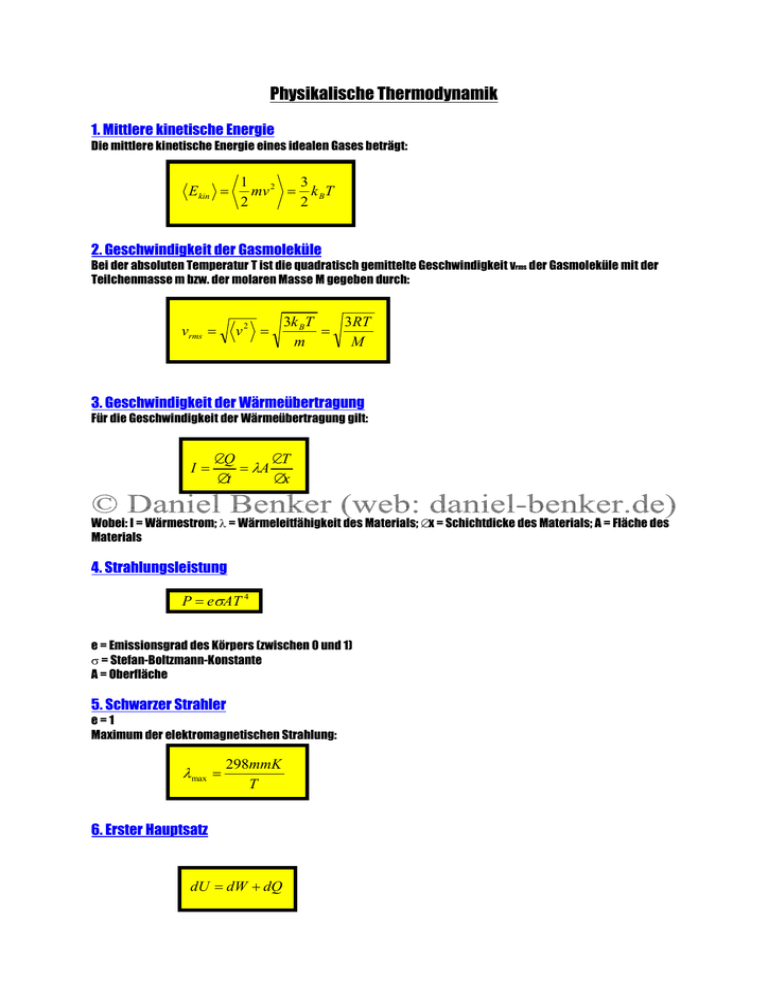
Physikalische Thermodynamik
1. Mittlere kinetische Energie
Die mittlere kinetische Energie eines idealen Gases beträgt:
E kin =
1 2
3
mv = k BT
2
2
2. Geschwindigkeit der Gasmoleküle
Bei der absoluten Temperatur T ist die quadratisch gemittelte Geschwindigkeit vrms der Gasmoleküle mit der
Teilchenmasse m bzw. der molaren Masse M gegeben durch:
vrms =
v2 =
3k BT
3RT
=
m
M
3. Geschwindigkeit der Wärmeübertragung
Für die Geschwindigkeit der Wärmeübertragung gilt:
I=
∆Q
∆T
= λA
∆t
∆x
Wobei: I = Wärmestrom; λ = Wärmeleitfähigkeit des Materials; ∆x = Schichtdicke des Materials; A = Fläche des
Materials
4. Strahlungsleistung
P = eσAT 4
e = Emissionsgrad des Körpers (zwischen 0 und 1)
σ = Stefan-Boltzmann-Konstante
A = Oberfläche
5. Schwarzer Strahler
e=1
Maximum der elektromagnetischen Strahlung:
λmax =
298mmK
T
6. Erster Hauptsatz
dU = dW + dQ
7. Innere Energie U
Die innere Energie eines Systems ist eine Zustandsfunktion. Das bedeutet: U hängt nur vom augenblicklichen
Zustand des Systems ab und nicht davon, wie dieser Zustand erreicht wurde. Zustandsfunktionen sind auch
Volumen, Druck und Temperatur. KEINE Zustandsfunktionen sind Wärme und Arbeit!
Die innere Energie eines idealen Gases hängt nur von seiner absoluten Temperatur ab. Bei realen Gasen und
auch Flüssigkeiten und Festkörpern hängt die innere Energie auch vom Druck und vom Volumen ab.
8. Adiabatengleichung
Bei einem reversiblen Prozess vollziehen sich die Änderungen so langsam, dass das System eine Reihe von
Gleichgewichtszuständen durchläuft. Jeder vom System einmal eingenommene Zustand lässt sich durch
infinitesimale Änderungen eines oder mehrerer Parameter in der umgekehrten Richtung wieder erreichen.
Während eines isobaren Prozesses bleibt der Druck konstant, und während eines isothermen Prozesses ändert
sich die Temperatur nicht. Bei einem adiabatischen Prozess wird keine Wärme zwischen System und
Umgebung übertragen.
Während der reversiblen adiabatischen Expansion eines idealen Gases gilt stets die Adiabatengleichung:
PV γ = const.
Darin ist γ der Quotient der Wärmekapazitäten bei konstantem Druck und konstantem Volumen:
γ=
CP
CV
9. reversible Expansion
Die Volumenarbeit eines reversibel expandierenden Systems ist gegeben durch:
W = − ∫ PdV
Im Falle der isothermen Expansion:
Wisotherm = − nRT ln
V2
V1
10. Wärmekapazität
Die Wärmekapazität bei konstantem Volumen entspricht der Änderung der inneren Energie mit der Temperatur:
CV =
∂U
∂T
Bei einem idealen Gas ist die Wärmekapazität bei konstantem Druck um nR größer als bei konstantem
Volumen:
C P = CV + nR
Die Wärmekapazitäten idealer Gase bei konstantem Volumen sind:
Einatomiges Gas:
3
CV = nR
2
Zweiatomiges Gas:
5
CV = nR
2
11. Gleichverteilungssatz
Befindet sich ein System im Gleichgewicht, so entfällt auf jeden Freiheitsgrad die mittlere Energie (½)kBT pro
Teilchen. Einatomige Gase haben drei Freiheitsgrade der kinetischen Energie. Zweiatomige Gase besitzen zwei
weitere Freiheitsgrade, nämlich die der Rotation um die beiden Achsen senkrecht zur Kernverbindungsachse.
Aus dem Gleichverteilungssatz folgt auch die Regel von Dulong und Petit: Die molare Wärmekapazität der
meisten Festkörper beträgt 3R. Dies kommt von den 6 möglichen Freiheitsgraden(je drei für die kinetische und
die potentielle Energie der Schwingung).
12. Zweiter Hauptsatz
Nach dem Zweiten Hauptsatz in der Formulierung von Clausius kann keine zyklisch arbeitende Kältemaschine
Wärme aus einem kälteren Reservoir in ein wärmeres Reservoir übertragen, ohne dass gleichzeitig Arbeit
zugeführt werden muss.
13. Entropie
Bei jedem irreversiblen Prozess geht das Universum in einen weniger geordneten Zustand über. Dieser hat eine
höhere Wahrscheinlichkeit. Ein Maß für die Unordnung eines Systems ist dessen Entropie. Sie ist eine
Zustandsfunktion. Die Entropieänderung ist definiert als
∆S = ∫
dQrev
T
Darin ist dQrev die dem System zu- oder abgeführte Wärmemenge, und zwar bei einem Prozess, der reversibel
zwischen dem jeweils betrachteten Anfangs- und Endzustand abläuft.
Die Entropie eines gegebenen Systems kann zu- oder abnehmen; die Entropie des Universums oder irgendeines
isolierten Systems allerdings kann niemals abnehmen. Bei einem reversiblen Prozess bleibt die Entropie des
Universums konstant; dagegen nimmt sie bei einem irreversiblen Prozess zu.
Bei einem irreversiblen Prozess steigt die Entropie SU des Universums, und die Wärmemenge
Wn = T∆SU
wird entwertet, kann also nicht mehr in Arbeit umgewandelt werden.
Die Entropie hängt mit der Wahrscheinlichkeit des betreffenden Zustands des Systems zusammen. Ein Zustand
höherer Ordnung tritt mit geringerer Wahrscheinlichkeit auf. Ein isoliertes System (ebenso das Universum)
strebt einem Zustand geringerer Ordnung, höherer Wahrscheinlichkeit und höherer Entropie zu.
14. Dritter Hauptsatz
Eine mögliche Formulierung des dritten Hauptsatzes ist das Nernstsche Wärmetheorem, nach dem jede ideal
kristallisierte reine Substanz am absoluten Nullpunkt die Entropie Null hat.