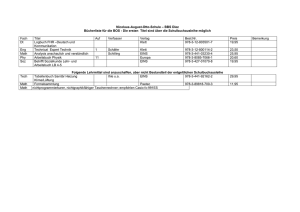
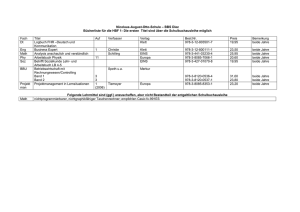
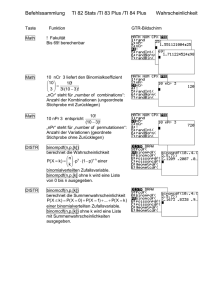
Kombinatorik (Inklusions-Exklusions

Kombinatorik (Inklusions-Exklusions-Prinzip)
Aufgaben: 5
> restart;
Anzahl surjektiver und injektiver Abbildungen
MATH: Hier ist ein Programm, welches rekursiv die Anzahl der surjektiven Abbildungen einer
Menge von n Elementen auf eine Menge von k Elementen ausrechnet.
> ansur:=proc(n::posint, k::posint)
if k>n then
return 0;
end if;
if k=1 then
return 1;
end if;
return (ansur(n-1,k-1)+ansur(n-1,k))*k;
end proc:
> map(i->ansur(i , 3),[$1..13]);
(1.1.1)
ÜBUNG [01]:
Beweise die Rekursion aus dem obigen Programm, d.h. zeige, dass die dort definierte Rekursion
tatsächlich die Anzahl der surjektiven Abbildungen einer Menge von Elementen auf eine
Menge von Elementen bestimmt.
MATH: Kann man die Anzahl
surjektiver Abbildungen von
bestimmen, kann man auch die Anzahl der Partitionen von
bestimmen, die dann
nach
in Klassen
ist.
> map(i->ansur(i,3)/3!,[$1..20]);
(1.1.2)
ÜBUNG [02]:
Schreibe ein alternatives Programm, welches die Anzahl
der Partitionen einer elementigen Menge in Klassen rekursiv berechnet. (Ohne Benutzung von ansur. Hinweis:
).
MATH: Will man nun die Menge aller Partitionen auf
zählen, so kann man das etwas
umständlich so machen:
> map(n->add(ansur(n,i)/i!,i=1..n),[$1..15]);
(1.1.3)
(1.1.3)
Hier ist ein Programm, welches etwas direkter vorgeht:
> part:=proc(n::posint)
if n=1 then
return 1;
end if;
return 1 + add(part(n-k)*binomial(n-1,k-1), k=1..n-1);
> end proc:
> map(part, [$1..15]);
(1.1.4)
ÜBUNG [03]:
Begründe die Richtigkeit des obigen Programms p a r t.
MATH: Wir wollen jetzt die Anzahl der surjektiven Abbildungen von einer -elementigen
Menge auf eine -elementige Menge genauer untersuchen.
> with(LinearAlgebra):
> M:=Matrix(10,10,(i,j)->ansur(i,j));
(1.1.5)
Wir vergleichen mit der Anzahl aller Abbildungen von
> A:=Matrix(10,10,(i,j)->j^i);
nach
:
(1.1.6)
Wir bekommen jetzt den Anfang einer Einsicht, wenn wir fragen, wie sich die Spalten von
denen von linearkombinieren:
> A^(-1).M;
aus
(1.1.7)
MATH: Dies ist ein sehr schönes Beispiel des Inklusions-Exklusions-Prinzips zum Abzählen.
Nehmen wir die dritte Spalte: Um die Menge aller surjektiven Abbildungen von
auf
zu zählen, zählen wir zuerst alle Abbildungen von
nach
, also .
Dann ziehen wir ab: Für jede 2-elementige Teilmenge von
die Anzahl der
Abbildungen, deren Bild in liegt. Also insgesamt
Zwischenbilanz:
.
.
Kritik: Wir haben die Anzahl der Abbildungen, die in eine einelementige Teilmenge von
gehen, nicht angemessen behandelt. Wir wollten sie gar nicht haben, hatten sie bei
einmal gezählt und dann bei
zweimal abgezogen. Wenn die Abbildung etwa nach
geht, geht sie auch nach
und nach
. Also werden wir sie wieder einmal für jede
einelementige Teilmenge hinzuaddieren müssen. Die Anzahl der einelementigen Teilmengen ist
aber
. Also bekommen wir:
.
Dies ist aber die Endbilanz. Es erklärt nicht nur die dritte Spalte der letzten Matrix, sondern
liefert ein Ergebnis für allgemeines .
ÜBUNG [04]:
1.) Diskutiere in gleicher Weise die vierte Spalte und die -te Spalte.
2.) Schreibe ein neues Programm
, das eine geschlossene Formel in für
fester Eingabe ausgibt.
bei
Übrigens zeigt
> limit((5+5^n-5*4^n+10*3^n-10*2^n)/5^n,n=infinity);
1
(1.1.8)
dass der (relative) Anteil der surjektiven Abbildungen von
auf
für große
praktisch gleich 1 ist, obwohl die absolute Anzahl der nicht surjektiven Abbildungen gegen
unendlich strebt.
> limit(5^n-(5+5^n-5*4^n+10*3^n-10*2^n),n=infinity);
(1.1.9)
DENKANSTOSS: Was sagen uns die -te Spalte der Matrix
> M^(-1).A;
(1.1.10)
über die Menge aller Abbildungen von
nach
Abbildung zerlegt sich gemäß der Bilder der Abbildungen.)
? (Hinweis: Die Menge dieser
ÜBUNG [05]:
1.) Du hast drei endliche Mengen
> op(map(i->C[i],[$1..3]));
(1.1.11)
einer Potenzmenge zusammen mit den Anzahlen der Elemente
> op(map(i->c[i],[$1..3]));
(1.1.12)
und den Anzahlen in den paarweisen Durchschnitten
> op(map(i->op(map(j->c[i,j],[$i+1..3])),[$1..2]));
(1.1.13)
und der Anzahl
>
(1.1.14)
>
(1.1.13)
> c[1,2,3];
c
(1.1.14)
der Elemente in dem Schnitt aller drei Mengen. Gib eine Formel für die Anzahl der Elemente
in der Vereinigung der drei Mengen an.
2.) Ist die Konfiguration
,
,
,
,
,
,
möglich?
Rationale Cauchy-Folgen/Nullfolgen
Aufgaben: 6
> restart;
Konvergente Folgen
MATH: Wir hatten bereits gesehen, daß < als angeordneter Körper nicht vollständig ist.
Außerdem hatten wir = als vollständigen angeordneten Körper, in welchem < dicht liegt,
axiomatisch eingeführt oder gefordert. Hier soll nun eine Konstruktion des Körpers der reellen
Zahlen als Vervollständigung des Körpers der rationalen Zahlen gegeben werden.
MATH: Eine rationalwertige Folge
, falls gilt:
Zu jedem
für alle
existiert ein
heißt konvergent gegen den Grenzwert
mit
.
Diese Bedingung fassen wir als ein Spiel auf: Der eine Spieler gibt ein
vor. Der andere
Spieler muss dann das bestimmen oder zeigen, dass es keines gibt. Es ist leider kein endliches
Spiel, denn der erste Spieler kann z.B. im Falle der Konvergenz sein immer wieder vergrößern.
Man kann das Spiel allerdings sehr gut mit MAPLE spielen.
Wir vergleichen die Folge
mit der Referenzfolge
wobei der Vegleich ein wenig subtil ist, weil alle
für
also unendlich viele Bedingungen gibt. Warum nehmen wir
mit
verglichen werden, es
als Vergleichsfolge?
> m:=50;
(2.1.1)
> an := [ [n, 1/n]$n=1..m ];
plot(an, y=0..m, style=point, symbol=circle);
Die Folge
ist postive rationale Nullfolge, denn offenbar gibt es für jedes
(hinreichend großes)
mit
. Und weil
,
monoton fallend ist, gilt sogar
ein
.
ÜBUNG [01]:
1.) Zeige:
ist konvergent mit Grenzwert 0, kurz eine rationale Nullfolge.
2.) Zeige: Konvergiert die Folge sowohl gegen als auch gegen , so gilt
.
MATH: Unsere Definition von Konvergenz hat einen großen Nachteil. Wir haben z. B. früher
schon gesehen, dass es eine rationale Folge gibt, welche gegen
konvergiert, aber
.
Cauchy-Folgen
MATH: Es entsteht also die Frage, wie wir rationale Folgen, die in konvergent sind, bereits im
Kontext der rationalen Zahlen charakterisieren können. Die Antwort sind die rationalen CauchyFolgen:
Eine rationalwertige Folge
Zu jedem
existiert ein
für alle
heißt Cauchy-Folge, falls gilt:
mit
.
DENKANSTOSS: Eine rationale Folge mit reellem Grenzwert ist rationale Cauchy-Folge.
BEISPIEL: Sei
eine Folge und
, dann ist
eine rationale Cauchy-Folge. Diese Cauchy-Folgen nennen wir von Dezimalbruchtyp.
DENKANSTOSS: Zeige dies!
> plot(map(i->[i, floor(sqrt(2)*10^i)/10^i], [$1..30]), style=
point, symbol=circle);
MATH: Die Menge aller Cauchy-Folgen
bezeichen wir mit
. Wir wollen
sehen, dass diese unter gliedweiser Addition und gliedweiser Multiplikation einen Ring bilden:
Seien
:
ÜBUNG [02]:
Zeige
.
MATH: Cauchy-Folgen sind beschränkt:
Wegen
für
gilt
für alle
für alle und ist beschränkt.
. Daher ist
ÜBUNG [03]:
Zeige
.
MAPLE: Der l i m i t-Befehl von Maple rechnet Grenzwerte aus, zumindest soweit Maple dazu
in der Lage ist. Wir werden ihn später noch brauchen.
> limit(1/i, i=infinity);
0
(2.2.1)
Manche Grenzwerte kann Maple nicht bestimmen:
> n->sum((1/i)^i, i=1..n);
limit(%(n), n=infinity);
(2.2.2)
Bei anderen Folgen wiederum erkennt Maple, dass es keinen Grenzwert gibt:
> limit(sin(1/n), n=0);
(2.2.3)
> limit(sin(1/n)/n, n=0);
undefined
(2.2.4)
Konstruktion von
MATH: Da in jeder Komponente die Ringaxiome erfüllt sind und die konstanten Folgen
und
beide in
liegen, ist
offenbar ein kommutativer Ring. Allerdings kein
Körper, denn Folgen, die den Wert Null annehmen kann man nicht invertieren. Schlimmer noch,
unsere Referenzfolge
hat zwar eine inverse Folge, nämlich
, aber diese ist keine Cauchyfolge mehr.
Idee: Es kommt bei den Cauchy-Folgen nur auf das ultimative Verhalten der Folge an. Daher
führen wir eine Äquivalenzrelation auf
ein:
ist Nullfolge.
DENKANSTOSS: Zeige, dass wirklich eine Äquivalenzrelation vorliegt. Benutze insbesondere
die Dreiecksungleichung, um Transitivität von w zu zeigen.
ÜBUNG [04]:
Gib zwei verschiedene Cauchyfolgen von Dezimalbruchtyp an, die äquivalent sind.
(Hinweis: Wann ist die Dezimalbruchentwicklung rationaler Zahlen nicht eindeutig?)
>
MATH: Summe und Produkt in
mit
1.)
2.)
sind verträglich mit ~, d.h.
,
DENKANSTOSS: 1.) ist offenbar einfach zu zeigen. Führe den Beweis von 2.) durch, indem du
die Kernidee
weiter ausführst.
MATH: Die Äquivalenzklassen bilden somit unter vertreterweiser Addition und Multiplikation
einen Ring, wie man leicht zeigt. Denn schwierig ist allenfalls die Vertreterunabhängigkeit der
Operationen, diese bekommt man aber sofort aus 1.) und 2.). Die Ringaxiome folgen
automatisch, da sie bereits für
gelten:
Die Menge der Äquivalenzklassen
ist ein kommutativer Ring mit 1.
Behauptung:
ist sogar ein Körper.
ÜBUNG [05]:
Zeige: Ist
keine Nullfolge, so ist
eine Cauchy-Folge, für die gilt:
.
MATH: Wir wollen diesem Körper noch eine Anordnung geben: Es gilt offenbar:
mit
.
Im ersten Fall wird man für die Äquivalenzklassen
definieren
im zweiten Fall
.
MATH: Die Axiome eines angeordneten Körpers sind erfüllt. Die Anordnung setzt die
Anordnung von < fort, indem wir
mit der Äquivalenzklasse der konstanten Folge
identifizieren.
DENKANSTOSS: Zeige dies.
Ohne Beweis behaupten wir:
MATH: Der angordnete Körper
ist vollständig und erfüllt das
Archimedische Axiom. Daher kann dieser Körper als = gewählt werden.
DENKANSTOSS: Zeige: Jede w -Klasse enthält eine Cauchy-Folge vom Dezimalbruchtyp.