Grundlegendes über Funktionen

2
Grundlegendes über Funktionen
Für die meisten Menschen beginnt die „richtige“ Mathematik beim ersten Auftreten von
Funktionen: Sobald man ein Funktionsschaubild hinzeichnen und Verläufe von Funktionen bestimmen kann, geht ihnen das mathematische Herz auf. Ich muss gestehen, dass ich
auch nicht ganz frei bin von dieser Denkweise, wenngleich ich betonen will, dass all das,
was Gegenstand des ersten Kapitels war, durchaus ernst zu nehmende Mathematik ist. Aber
dennoch will ich gern einstimmen in den Chor derer, die sagen: „Jetzt geht’s richtig los!“
Das Problem ist allerdings: Kaum ist die Freude über das Auftreten der Funktionen verflogen, beginnt der Bammel vor denselben: Was ist das eigentlich, eine Funktion, was für
wichtige Eigenschaften kann sie haben, welche speziellen Funktionen muss man kennen
usw.?
Diese Befürchtungen sind aber wirklich nicht begründet, Funktionen etwas „ganz Normales“. Um Ihnen ein Gefühl dafür zu geben, beginne ich mit einem ganz einfachen Beispiel; stellen Sie sich vor, Sie fahren mit Ihrem Auto einige Stunden lang mit der konstanten
Geschwindigkeit von  km/h. (Ich weiß, dass das heutzutage schwer vorstellbar ist, aber
versetzen Sie sich einfach mal gedanklich ins Innere Australiens, da geht so was.) Zur Berechnung des nach einer Zeit von t Stunden zurückgelegten Weges von s Kilometern kann
man dann die Formel
s =  ⋅ t
aufstellen, wobei ich nach bester Mathematiker-Manier großzügig auf die Einheiten verzichtet habe. Bei Anwendungen, diese Warnung möchte ich hier gleich anbringen, sollte
man die physikalischen Einheiten allerdings sicherheitshalber stets mitführen, entweder
explizit auf beiden Seiten oder in eckigen Klammern für die ganze Gleichung.
Mit obiger Formel kann man ausrechnen, dass Sie nach einer Stunde 120 Kilometer zurückgelegt haben, nach zwei Stunden 240 Kilometer und beispielsweise nach fünf Stunden
600 Kilometer. Es ist aber ebenso gut möglich, auszurechnen, wie weit Sie nach einer halben Stunde gekommen sind (nämlich  ⋅  = , also 60 km), wie weit nach einer Minute
G. Walz, F. Zeilfelder, T. Rießinger, Brückenkurs Mathematik,
DOI 10.1007/978-3-642-41564-7_2, © Springer-Verlag Berlin Heidelberg 2014
35
36
2 Grundlegendes über Funktionen
(2 km), und wenn Sie Lust haben auch die zurückgelegte Strecke nach einer Sekunde oder
Stunden. Sie sehen also, dass man für t jeden beliebigen positiven Wert einauch nach 

setzen kann, und abhängig von diesem Wert liefert die Formel die zugehörige Strecke s.
Um diese Abhängigkeit stärker zu betonen, schreibt man meist
s(t) =  ⋅ t,
(2.1)
und schon haben wir – heimlich, still und leise – das erste Beispiel einer Funktion gesehen.
Da t hier von überhaupt nichts abhängt, nennt man es auch die unabhängige Variable,
entsprechend s die (von t) abhängige Variable; für jeden beliebigen Eingabewert von t, mit
dem Sie die Funktion füttern, liefert diese Ihnen einen eindeutig bestimmten Ausgangswert s. Genau das ist das Wesen einer Funktion, und das werde ich im nächsten Abschnitt
erst einmal präzise hinschreiben.
2.1 Definitionsbereich, Wertevorrat und Bildmenge
Da es im Leben nicht nur Autos und gefahrene Zeiten gibt (was man bei manchen Leuten
allerdings glauben könnte), nennt man die unabhängige Variable in der Mathematik meist
x (und nicht t) und die Funktion bezeichnet man mit f (und nicht s).
Funktion, Definitionsbereich und Wertevorrat
Es seien D und W Mengen, die nicht leer sein sollten; üblicherweise, aber nicht zwingend notwendig, werden das Mengen von Zahlen sein. Eine Funktion f ist eine
Vorschrift (Abbildungsvorschrift, Formel, . . . ), die jedem Element x der Menge D
auf eindeutig bestimmte Art und Weise ein Element y = f (x) von W zuordnet.
Man nennt D den Definitionsbereich von f (weil f für alle Werte x aus D definiert sein soll) und W den Wertevorrat von f , weil y als Funktionswert von x
bezeichnet wird und W eben alle möglichen Funktionswerte von f in sich versammelt.
Oft schreibt man kurz f ∶ D → W und hat so auf einen Schlag Definitionsbereich
und Wertevorrat von f definiert. Ich werde das im Folgenden gelegentlich, aber nicht
immer so tun.
Ich vermute, Sie brauchen jetzt erst mal einen starken Kaffee, um das Gelesene zu verdauen. Vielleicht kann ich Ihnen aber auch mit ein paar Beispielen helfen:
Beispiel 2.1: Ich wähle erst mal der Bequemlichkeit halber sowohl als Definitionsmenge
als auch als Wertevorrat die Menge der reellen Zahlen, also D = W = R. Die erste Abbil-
2.1 Definitionsbereich, Wertevorrat und Bildmenge
37
dungsvorschrift, die ich testen will, ist
f ∶ R → R,
f (x) = x.
Das ist nun eine Funktion reinsten Wassers, denn sie weist jeder reellen Zahl x einen eindeutig bestimmten Wert zu, nämlich das Doppelte von x, und dieser Wert liegt auch im
∎
zulässigen Wertebereich, nämlich der Menge der reellen Zahlen.
Ursprünglich hatte ich an dieser Stelle vorgesehen, in einer Übungsaufgabe einige Funktionswerte von f berechnen zu lassen, aber das scheint mir jetzt doch zu kindisch.
Beispiel 2.2: Stattdessen ein zweites Beispiel, die Abbildungsvorschrift sei dieses Mal
f ∶ R → R,
f (x) = x  .
Auch dieses ist eine Funktion, denn jedem reellen Eingabewert x wird eine eindeutige Zahl,
nämlich gerade sein Quadrat, zugewiesen. Dennoch weist dieses Beispiel eine Neuigkeit
auf: Getreu der Regel „Minus mal Minus ergibt Plus“ treten hier als Funktionswerte näm∎
lich niemals negative Zahlen auf, obwohl sie prinzipiell durchaus zugelassen wären.
Es ist also wichtig zu betonen, dass der Wertevorrat W die Menge aller als Funktionswert
zugelassenen Zahlen enthält, diese müssen aber nicht unbedingt auch wirklich von der
Funktion „getroffen“ werden. Das sollte festgehalten werden:
Der Wertevorrat muss nicht ausgeschöpft werden
Der Wertevorrat W einer Funktion enthält die Menge aller potenziellen Funktionswerte; er kann durchaus Zahlen enthalten, die niemals als Funktionswert auftreten.
Die Menge aller Elemente von W, die tatsächlich als Funktionswert auftreten, bezeichne ich als Bildmenge von D und symbolisiere sie mit f (D).
Die Bildmenge der Funktion f (x) = x  ist also gerade die Menge der nicht negativen
reellen Zahlen.
Ich gebe zu, dass die feinsinnige Unterscheidung zwischen Wertevorrat und Bildmenge
nicht jedermanns Lieblingsthema ist, aber wichtig ist sie eben doch; schlimmer noch: Die
Bezeichnungsweise und Notation ist in der Literatur nicht einheitlich, und es kann Ihnen
durchaus passieren, dass später einmal ein Dozent oder Fachbuchautor das, was ich hier als
Wertevorrat bezeichne, lieber Wertebereich nennen wird, die Bildmenge wiederum heißt
dann vielleicht Wertemenge usw. Ich kann’s nicht ändern, Sie müssen einfach immer sorgfältig schauen, was der jeweilige Autor am Anfang des Textes definiert.
Ein weiteres, ziemlich eintöniges, aber korrektes Beispiel einer Funktion, die ihren Wertevorrat nicht ausschöpft, ist das folgende: Es sei D = R, W = {, , } und f (x) = .
38
2 Grundlegendes über Funktionen
Was ist hier los? Nun, dies ist sicherlich eine Funktion, denn es wird jeder reellen Zahl x
in eindeutiger Weise ein Wert zugeordnet, nämlich die Zahl . Der Wertevorrat dieser
Funktion ist schon nicht allzu groß, er umfasst nur drei Zahlen, und dennoch schöpft sie
ihn nicht aus, denn die Zahlen  und  treten niemals als Funktionswert in Erscheinung.
Hier ist also die Bildmenge gerade die ein-elementige Menge {}.
Sehr oft ist der Definitionsbereich einer Funktion ein Intervall, und diesen Begriff sowie
die damit zusammenhängende Bezeichnungsweise will ich an dieser Stelle gleich einführen:
Intervall
Sind a und b reelle Zahlen, wobei a kleiner oder gleich b sein soll, also a ≤ b, so nennt
man die Menge aller reellen Zahlen, die zwischen a und b liegen, das Intervall mit
den Grenzen a und b.
Gehören a und b selbst auch zu diesem Intervall, so nennt man dies ein abgeschlossenes Intervall und bezeichnet es mit eckigen Klammern:
[a, b] = {x ∈ R mit a ≤ x ≤ b}.
Gehören a und b nicht zu diesem Intervall, so nennt man dies ein offenes Intervall
und bezeichnet es mit runden Klammern:
(a, b) = {x ∈ R mit a < x < b}.
Auch die Mischformen
(a, b] = {x ∈ R mit a < x ≤ b}
und
[a, b) = {x ∈ R mit a ≤ x < b}
existieren, man nennt sie halboffene Intervalle.
Mithilfe dieser Notation kann man also beispielsweise eine Funktion, deren Definitionsbereich die Menge aller rellen Zahlen zwischen 2 und 3 (unter Einschluss dieser beiden)
sein soll, kurz in der Form
f ∶ [, ] → R
notieren.
Wie wäre es denn an dieser Stelle mit einem kleinen mental snack zwischendurch?
2.1 Definitionsbereich, Wertevorrat und Bildmenge
39
Übungsaufgabe 2.1: Bestimmen Sie die genaue Bildmenge der Funktion
f ∶ [−, ] → R,
f (x) =

.
x −
∎
Wenn Sie nun so langsam denken, dass so ziemlich alles unter der Sonne, was mit
„ f (x) =“ losgeht, eine Funktion ist, so muss ich Ihnen das Folgende zeigen:
Es sei D = R , W = {−, } und für alle x ∈ D
f (x) =  oder −, je nachdem, wie ich mich fühle.
Das ist nun sicherlich keine eindeutige Vorschrift zur Ermittlung des Wertes f (x), denn
woher sollen Sie wissen, wie ich mich fühle, ich weiß es ja selbst oft nicht so genau; somit
ist f keine Funktion.
Aber auch die folgenden beiden, wieder eher mathematisch angehauchten Beispiele stellen – aus unterschiedlichen Gründen – keine Funktionen dar:
Setzen wir beispielsweise
g ∶ N → N,
g(x) =
√
x,
√
so stellt sich relativ schnell heraus, dass beispielsweise
der Wert g(), also , nicht im
√
angegebenen Wertevorrat von g liegt, denn  ist keine natürliche Zahl (nicht einmal eine
rationale, aber darauf kommt’s jetzt auch nicht mehr an).
Aber auch wenn ich den Definitionsbereich und den Wertevorrat von g erweitere zu D =
W = R, erweise ich der Möchtegern-Funktion einen Bärendienst, denn jetzt ist sie nicht
mal mehr auf der gesamten Menge D definiert, da reelle Wurzeln aus negativen Zahlen
nicht erklärt sind.
Sie sehen also, man muss die Funktionsvorschrift stets im Zusammenhang mit dem
Definitionsbereich und dem Wertevorrat prüfen, um sicher sagen zu können, ob es sich
wirklich um eine Funktion handelt. Und – um doch einmal in den bei vielen Autoren beliebten Krankenschwestern-Plural zu verfallen – das wollen wir doch gleich noch ein wenig
üben:
Übungsaufgabe 2.2: Welche der folgenden Vorschriften stellt eine Funktion dar?
a) f ∶ N → N, f (x) = x 
b) g ∶ [−, ] → R, g(x) = x
c) h ∶ Q → Q, h(x) = x  −  x  +  x
∎
Liegen sowohl der Definitionsbereich als auch der Wertevorrat einer Funktion in den
rellen Zahlen – man sagt dann auch kurz, es handle sich um eine reelle Funktion –, so
kann man ihren Verlauf auch bildlich darstellen. Wenngleich Sie das ganz sicher von verschiedensten Gelegenheiten her bereits kennen, will ich es hier der Vollständigkeit halber
kurz aufschreiben:
40
2 Grundlegendes über Funktionen
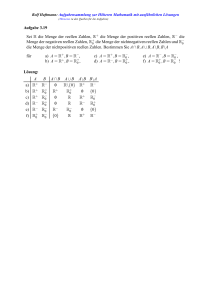
f (x)
2
1
−3
−2
−1
1
2
3
x
−1
Abb. 2.1 Graph einer Funktion
Man beginnt damit, ein Koordinatensystem zu zeichnen, also zwei senkrecht zueinander stehende Achsen, die sich üblicherweise im jeweiligen Nullpunkt schneiden. Auf
diesen nimmt man durch Markierung von mindestens einer Zahl eine Einteilung vor. Die
horizontale, nach rechts gerichtete Achse bezeichnet man meist als x-Achse, da man darauf die x-Werte markiert, die vertikale, nach oben gerichtete Achse heißt meist y-Achse, da
man zumindest in früherer Zeit die Funktionswerte, welche man auf dieser Achse markiert,
nicht als f (x), sondern einfach als y bezeichnete.
Nach dem großen Philosophen und Mathematiker René Descartes, dessen Name in
damals üblicher Weise latinisiert wurde zu Renatus Cartesius, nennt man ein derartiges
Koordinatensystem auch kartesisches Koordinatensystem.
Um sich nun im wahrsten Sinne des Wortes ein Bild vom Verlauf einer Funktion zu
machen, interpretiert man für jedes x aus dem Definitionsbereich der Funktion das Zahlenpaar (x, f (x)) als Koordinaten eines Punktes in diesem gerade gezeichneten System
und zeichnet diesen Punkt ein. So ergeben sich beispielsweise für die Funktion f (x) = x
die Paare (, ), (, ), (−, −) und (, ).
Macht man das nicht nur für vier, sondern für ganz viele ganz dicht beieinander liegende Pärchen, so ergeben die solchermaßen gezeichneten Punkte bei nicht allzu verrückten
Funktionen eine durchgehende Linie, die man als Schaubild oder Graph der Funktion bezeichnet. Ein ziemlich willkürlich gewähltes Beispiel sehen Sie in Abb. 2.1.
Übrigens schreibt man auch nach der vor ein paar Jahren eingeführten neuen Rechtschreibung das Wort „Graph“ mit „ph“, ganz im Gegensatz zu so schönen damit verwandten
Wörtern wie „grafisch“ oder „Biografie“. Meiner persönlichen Vermutung nach liegt das
einfach daran, dass in der „f “-Schreibweise der Ausdruck „Graf von f “ doch gar zu sehr
an „Graf von Monte Christo“ erinnern würde.
Aber nun zurück zur Mathematik.
2.2 Verkettung von Funktionen; Monotonie und Umkehrbarkeit
41
2.2 Verkettung von Funktionen; Monotonie und Umkehrbarkeit
Nehmen wir einmal an, Sie sind glücklicher Inhaber einer kleinen Firma, die für eine Reihe stark nachgefragter Produkte das Monopol besitzt, und sie wollen die Preise für Ihre
Produkte neu kalkulieren. Da Sie ordentlich verdienen wollen, gehen Sie dabei wie folgt
vor: Zuerst wird der alte Preis um 100 erhöht, und danach wird das Ganze noch mal verdreifacht. (Sollte Ihnen das unverschämt erscheinen, so bin ich ganz Ihrer Meinung, aber
beispielsweise machen das die Ölkonzerne bei der Neubestimmung ihrer Benzinpreise genauso.)
Da Sie heimlich ein Mathematikbuch gelesen haben, beschreiben Sie diese beiden Operationen jeweils durch eine Funktion, die auf der Menge der positiven Zahlen definiert sein
soll: Ist x der alte Preis, so lautet die zuerst anzuwendende Funktion
g(x) = x + ,
und die zweite ist
f (y) =  ⋅ y.
So berechnen Sie beispielsweise für x = , dass g(x) =  und f () =  ist; ein
Produkt, das vorher  Euro kostete, schlägt jetzt mit  Euro zu Buche.
So können Sie das nach und nach mit allen Produktpreisen machen. Beispielsweise
kommt ein Produkt, das eingangs x =  Euro kostete, nach Ihrer kleinen Neukalkulation auf g(x) =  und schließlich f () =  Euro.
Allerdings fällt Ihnen wohl ziemlich bald auf, dass Sie die zwischenzeitliche Bestimmung von g(x) eigentlich weglassen können und lieber gleich den Ausgabewert von g
wieder in f hineinstecken können. Was Sie dabei machen, nennt man in der Mathematik die Verkettung der Funktionen g und f . Die durch die Verkettung entstandene neue
Funktion nenne ich für den Moment h; ich berechne sie explizit, indem ich g(x) in f hineinstecke und ausrechne:
h(x) = f (g(x)) = f (x + ) =  ⋅ (x + ) = x + .
Es ist also
h(x) = x + ,
und auch diese Funktion ist auf der Menge aller positiven Zahlen definiert. In dieser Darstellung können Sie nun etwas schneller als oben nachrechnen, dass h() =  und
h() =  ist.
So geht das prinzipiell für alle Funktionen der Welt, wobei nur gewährleistet sein muss,
dass die Funktion f mit dem Ausgabewert von g etwas anzufangen weiß, dass also die
Bildmenge von g im Definitionsbereich von f liegt.
42
2 Grundlegendes über Funktionen
Das sollte ich jetzt wirklich mal präzise aufschreiben:
Verkettung von Funktionen
Es seien f ∶ F → W und g ∶ D → E zwei Funktionen mit der Eigenschaft, dass der
Definitionsbereich F von f im Bildbereich g(D) von g liegt.
Dann heißt die Funktion f ○ g ∶ D → W, definiert durch
f ○ g ∶ D → W,
f ○ g(x) = f (g(x))
für alle x ∈ D, die Verkettung von f und g; gelegentlich sagt man auch Hintereinanderausführung oder Komposition.
Zu beachten ist die Reihenfolge: Es wird zuerst g und danach f angewendet.
Ich habe keine Ahnung, wie man das Zeichen ○ aussprechen soll, ich habe es in meinem
Leben bisher immer nur hingeschrieben. Manche Leute sagen dazu „Kringel“, andere „verknüpft mit“, und wieder andere sagen einfach „nach“, „ f ○ g“ wird also in diesem Fall als „ f
nach g“ ausgesprochen. Das ist gar nicht so schlecht, wie es auf den ersten Blick scheinen
mag, denn es verdeutlicht noch mal die Reihenfolge, in der die beiden Funktionen nacheinander auszuführen sind: Zuerst g und danach f . Das macht man gerade am Anfang oft
falsch, da man eben von links nach rechts zu lesen gewohnt ist (möglicherweise machen
Japaner hier weniger Fehler, ich weiß es nicht). Die Schreibweise ( f ○ g)(x) soll suggerieren, dass zunächst g auf x angewendet wird, weil es direkt daneben steht, und erst danach
f an die Reihe kommt.
Bevor ich mich nun weiter in philosophische Betrachtungen über Vor- und Nachteile
dieser Schreibweise verliere, lieber Beispiele; um diese etwas kompakter hinzuschreiben,
möchte ich gerne für die Menge der nicht negativen reellen Zahlen das Symbol R+ einführen, also
R+ = {x ∈ R; x ≥ }.
Dann kann’s losgehen:
Beispiel 2.3: Betrachten wir die Funktionen
g ∶ R → R,
g(x) = (x + )
und
f ∶ R+ → R,
f (y) =
√
y − .
Da die Bildmenge von g gerade die nicht negativen reellen Zahlen sind („Minus mal Minus . . . “!), kann ich unbesorgt f mit g verketten und erhalte:
√
( f ○ g) ∶ R → R, ( f ○ g)(x) = f ((x + ) ) = (x + ) −  = x +  −  = x + ,
2.2 Verkettung von Funktionen; Monotonie und Umkehrbarkeit
43
also ( f ○ g)(x) = x + . Die Verkettung bewirkt also gerade mal die Erhöhung von x um .
Sie müssen zugeben, dass wir hier gegenüber der separaten Auswertung von f und g eine
∎
Menge Arbeit gespart haben!
Beispiel 2.4: Jetzt seien
√
+
g ∶ R → R,
g(x) =
x+
x +
und
f ∶ R ∖ {} → R,
f (y) =

.
y
Die Funktion f verdaut als Eingabewert jede reelle Zahl außer der Null, und da diese als
Wert von g nicht vorkommt, brauchen wir uns um das Zusammenpassen der Bereiche keine Sorgen zu machen; das Berechnen bzw. Vereinfachen der Verkettung mache ich jetzt
mal in Einzelschritten: Setzt man g(x) in f ein, so wird g(x) quadriert und in den Nenner gepackt; das Quadrieren hebt aber gerade die Wurzelbildung auf, sodass der Nenner
heißt. Und da man durch einen Bruch dividiert, indem man mit seinem
von f jetzt x+
x+
Kehrbruch multipliziert, erhalten wir als Ergebnis:
( f ○ g) ∶ R+ → R,
( f ○ g)(x) =
x +
.
x +
∎
Vielleicht haben Sie sich die ganze Zeit schon gefragt, was passiert, wenn man in obigen
Beispielen bei der Verkettung die Reihenfolge der verketteten Funktionen vertauscht? Zu
spät, ich war schneller und frage Sie:
Übungsaufgabe 2.3: Prüfen Sie bei den in den obigen Beispielen behandelten Funktionenpaaren, ob auch die Verkettung g ○ f möglich ist; falls ja, geben Sie die verkettete Funk∎
tion möglichst einfach an.
Eine gewisse Sonderrolle bei der Verkettung von Funktionen spielt die so genannte Umkehrfunktion einer Funktion. Das ist diejenige Funktion, die eine gegebene Funktion durch
Verkettung wieder rückgängig macht; ich werde das gleich noch genauer definieren, erst
mal ein paar Beispiele:
Verkettet man die Funktion
g ∶ R → R,
g(x) = x − 
mit der ebenfalls auf ganz R definierten Funktion f (y) = y + , so ergibt sich
( f ○ g) ∶ R → R,
( f ○ g)(x) = (x − ) +  = x
44
2 Grundlegendes über Funktionen
und ebenso
(g ○ f ) ∶ R → R,
(g ○ f )(x) = (x + ) −  = x.
Die Verkettung der beiden Funktionen lässt also unabhängig von der Reihenfolge jedes x
unverändert, so als ob gar keine Funktion angewandt worden wäre. Anders formuliert: Die
jeweils zuerst angewandte Funktion wird durch die Anwendung der zweiten umgekehrt.
Das ist natürlich völlig unabhängig von der speziellen Zahl 28 und entspricht im Übrigen
völlig der täglichen Lebenserfahrung: Wenn Sie beispielsweise im Roulette einen bestimmten Betrag gewinnen und diesen im nächsten Spiel gleich wieder komplett verlieren, so hat
sich insgesamt an Ihrer finanziellen Situation nichts geändert, getreu dem alten Sprichwort:
„Wie gewonnen, so zerronnen.“
Auch im nächsten Beispiel klappt das mit dem Umkehren noch ganz gut: Um die Funktion
g ∶ R → R,
g(x) = −x
wieder umzukehren, muss man sie nur mit der Funktion f (y) = −  y verketten, denn dann
ist für alle x ∈ R:
( f ○ g) ∶ R → R,

( f ○ g)(x) = − ⋅ (−x) = x

und ebenso
(g ○ f ) ∶ R → R,

(g ○ f )(x) = − ⋅ (− x) = x.

Alles schön und gut, werden Sie sagen, wo ist das Problem? Die Probleme kommen noch,
keine Sorge. Zuvor wird es aber höchste Zeit, den Begriff Umkehrfunktion exakt zu definieren. Dabei sollen natürlich die gerade betrachteten Beispiele als Leitfaden dienen.
Umkehrfunktion
Es sei f eine Funktion mit dem Definitionsbereich D und der Bildmenge f (D). Eine
Funktion, nennen wir sie f − , deren Definitionsbereich f (D) ist und die die Eigenschaft
( f − ○ f )(x) = x
für alle x ∈ D hat, nennt man Umkehrfunktion von f . Existiert zu einer Funktion f
eine Umkehrfunktion, so nennt man f selbst umkehrbar.
Nicht jede Funktion ist umkehrbar.
http://www.springer.com/978-3-642-41563-0