Übungen zu Mathematische Methoden der Physik 1 / Blatt 2 / 14

Übungen zu Mathematische Methoden der Physik 1 / Blatt 2 / 14. März 2005 / GG
Binomialverteilung, Geometrische Verteilung
1. Ein instabiler Atomkern sei nach Ablauf einer Zeit τ mit der Wahrscheinlichkeit x ∈ [0, 1] zerfallen.
Der W-raum (Ω, W ) dieses Vorgangs ist Ω = {0, 1} mit dem W-maß W , für das W ({1}) = x gilt.
Die Zahl 1 steht also für das Elementarereignis „Der Kern ist zerfallen”.
(a) Welchen Erwartungswert und welche Varianz hat Z : Ω → R, ω 7→ ω?
(b) Wenn N unterscheidbare Kerne sich gegenseitig nicht beeinflussen, hat die Frage „Welche der
N Kerne zerfallen innerhalb der Zeit τ ?” den W-raum (ΩN , WN ) mit
ΩN := ΩN und WN (A1 × .. × AN ) :=
N
Y
W (Ai ).
i=1
Die Zahl der in einem Elementarereignis (ω 1 , .., ω N ) ∈ ΩN zerfallenen Kerne wird von der
PN
stochastischen Variablen ZN : ΩN → R mit ZN (ω 1 , .., ω N ) := i=1 Z(ω i ) angegeben. Welchen
Erwartungswert und welche Varianz hat ZN ? Hinweis:
⎞
⎛
⎞
Ã
! ⎛
X
X
X
X
f (α) · g (β) · . . . · h (γ) =
f (α) · ⎝
g (β)⎠ · . . . · ⎝
h (γ)⎠
α∈A
α∈A,β∈B,...γ∈C
γ∈C
β∈B
(c) Zeigen Sie, dass der Transport von WN mit ZN die Binomialverteilung auf {0, 1, .., N } ist. Es
gilt für k ∈ {0, 1, .., N }
−1
({k})) = Bi (k; N, x) := xk (1 − x)N−k
WN (ZN
N!
.
(N − k)!k!
−1
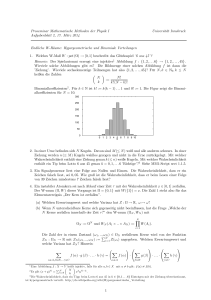
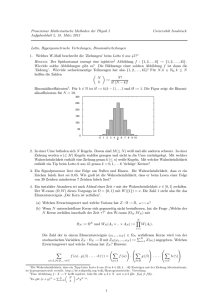
({k})) für N = 10 und N = 100 und
Die Figuren zeigen die Binomialverteilung k 7→ WN (ZN
x = 1/3 und x = 2/3.
(d) Sei nun x = 10−3 . Welchen Wert hat die Wahrscheinlichkeit, dass von N = 103 Kernen
innerhalb der Zeit τ mehr als 2 (bzw. 3) zerfallen? Hinweis: Berechnen Sie zunächst die
Wahrscheinlichkeit des komplementären Ereignisses.
(e) Kontrollieren Sie Ihr Ergebnis für d) an der Chebyshev Ungleichung1 .
2. Ein instabiler Atomkern, zerfalle unabhängig von seinem Alter in einer Sekunde mit der Wahrscheinlichkeit (1 − x) ∈ ]0, 1[. Die Wahrscheinlichkeit, dass er n ∈ N0 Sekunden überlebt und dann bis
zum Zeitpunkt n + 1 zerfällt, ist p(n) := W ({n}) := xn (1 − x). (Geometrische Verteilung zum
Parameter x)
(a) Sei N ∈ N0 gegeben. Mit welcher Wahrscheinlichkeit zerfällt der Kern vor der Zeit N + 1?
Gilt W (N0 ) = 1?
(b) Die stochastische Variable τ := idN0 heißt Lebensdauer. Welchen Erwartungswert und welche
Varianz hat τ ? Hinweis:
∞
X
n=0
nxn = x
∞
∞
∞
X
d X n
d2 X n
x and
n(n − 1)xn = x2 2
x
dx n=0
dx n=0
n=0
(c) Skizzieren Sie den Graphen der Verteilung p (von τ ).
(d) Seien M, m ∈ N0 gegeben. Mit welcher Wahrscheinlichkeit zerfällt ein Kern, der den Zeitpunkt
M erlebt, bis zum Zeitpunkt M + m? Hinweis: Die bedingte Wahrscheinlichkeit W (A | B) =
W (A∩B)
W (B) für A = {n ∈ N0 | n < M + m} und B = {n ∈ N0 | n ≥ M } ist zu ermitteln. Sind A
und B stochastisch unabhängig? Mit welcher Wahrscheinlichkeit zerfällt ein Kern im Intervall
M ≤ n < M + m?
1 Für
eine reelle stochastische Variable f auf einem endlichen Wahrscheinlichkeitsraum (Ω, W ) sagt diese
W ({ω ∈ Ω : |f (ω) − hf i| ≥ t}) ≤ V(f )t−2 .
1
x=1/3
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
6
7
8
9
10
6
7
8
9
10
k
x=2/3
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
k
Figure 1:
x=1/3
0.1
0.08
0.06
0.04
0.02
0
-20
0
20
40
60
80
100
120
60
80
100
120
k
x=2/3
0.1
0.08
0.06
0.04
0.02
0
-20
0
20
40
k
Figure 2:
2