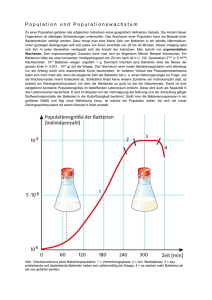
Aufgabe 27 In einem kleinen Teich lebt eine Bakterienpopulation

Stochastische Prozesse - Übung
Andrea Wiencierz
Blatt 9
WS 2009/10
Aufgabe 27
In einem kleinen Teich lebt eine Bakterienpopulation. Die Population verschwindet niemals vollständig,
d.h. es ist immer mindestens ein Bakterium vorhanden. Der Teich bietet aber nur Nahrung und Lebensraum für N Bakterien, weshalb niemals mehr als N Stück vorkommen. Die Bakterien vermehren
sich durch Teilung mit der Rate λi = λi , i = 1, . . . , N − 1, wobei sich nie mehrere Bakterien gleichzeitig
teilen. Die Teilung verlangsamt sich also mit der Anzahl der vorhandenen Bakterien.
µ
Die Bakterien dienen als Nahrung für räuberische Einzeller, die sie mit der Rate µi = (N +1−i)
,
i = 2, . . . , N fressen, wobei auch dieses Ereignis niemals gleichzeitig vorkommt. Es werden also weniger Bakterien gefressen, wenn die Bakteriendichte niedriger ist.
(a) Welcher stochastische Prozess beschreibt die Anzahl X(t) der zum Zeitpunkt t lebenden Bakterien?
(b) Geben Sie die Intensitätsmatrix Λ und die Übergangsmatrix Q der eingebetteten Markov-Kette an.
(c) Schreiben Sie eine Funktion in R, die diesen Prozess in Abhängigkeit der Parameter µ und λ sowie
der maximalen Populationsgröße N simuliert.
Simulieren Sie Realisierungen des Prozesses mit N = 100, λ = 1.5, µ = 1, n = 1000, je für die
Startwerte X(0) = 1, X(0) = 51 und X(0) = 100. Stellen Sie die Pfade graphisch dar.
(d) Nehmen Sie nun an, dass die räuberischen Einzeller selbst ausgestorben sind. Wie lange würde
es dann erwartungsgemäß dauern, bis die Bakterienpopulation von X(0) = 1 auf 50 bzw. von
X(0) = 51 auf 100 Bakterien angewachsen ist?
Aufgabe 28
Schreiben Sie eine R-Funktion, die für einen diskreten Markov-Prozess mit Zustandsraum S = {1, . . . , N }
und Intensitätsmatrix Λ die Matrix P (t) der Übergangswahrscheinlichkeiten berechnet.
Hinweis: Eine Eigenwertzerlegung kann in R mithilfe der Funktion eigen() durchgeführt werden.
(a) Wenden Sie Ihre R-Funktion auf die Situation in Aufgabe 27 c) an. Bestimmen Sie P (t) für verschiedene t.
(b) Vergleichen Sie die in a) berechneten exakten Übergangswahrscheinlichkeiten mit der Approximation aus Satz 4.7 des Vorlesungsskripts.
Aufgabe 29
Betrachten Sie in Folgenden erneut das Hamsterlabyrinth aus den Aufgaben 18 und 22. In den vier
Ecken des Labyrinths sind nun Nüsse und Hirse deponiert, sodass die Neigung des Hamsters diese
Räume zu verlassen nur halb so groß ist wie bei den anderen Räumen des Labyrinths.
Die Hamsterläufe können nun als Realisierungen eines Markov-Prozesses betrachtet werden, mit der aus
Aufgaben 18 und 22 bekannten homogenen Markov-Kette als eingebettete Markov-Kette. Dabei sind
die zustandsabhängigen Intensitäten λi gegeben als λ1 = λ3 = λ7 = λ9 =: λ2 (Eckräume mit Nüssen
und Hirse) und λ2 = λ4 = λ5 = λ6 = λ8 =: λ (andere Labyrinthräume).
(a) Bestimmen Sie die Intensitätsmatrix dieses Markov-Prozesses sowie die Matrix P (t) der Übergangswahrscheinlichkeiten zu einem Zeitpunkt t ≥ 0 für λ = 2, mithilfe der obigen R-Funktion.
(b) Wieviel Zeit braucht der Hamster im Mittel, um in vier Schritten von Raum 1 zu 9 zu gehen?
22.12.2009
Seite 1