Informationstheorie

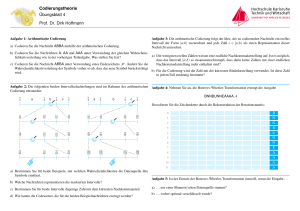
Informationstheorie - (P)Review
Contact:
Rolf S. Adelsberger
[email protected]
1
1.1
1.1.1
Looking Back:
Vorlesung
Arithmetic Coding
X = {a, e, i, o, u}
x P (X = x)
a
0.12
e
0.42
i
0.09
o
0.30
0.07
u
1.1.2
Beispiel von Slide 18
0.12 a
0.0
0.54
0.5967
0.12
0.5508
0.59994
0.54
0.63
0.5886
0.5967
0.61128
0.61371
0.93
1.0
0.6237
0.63
0.62181
0.6237
0.42 e
0.09 i
0.30 o
0.07 u
"i"
"o"
1
"u"
0.12 a
1.0
0.46
0.4033
0.88
0.4492
0.40006
0.46
0.4114
0.38872
0.37
0.4033
0.38629
0.07
0.0
0.3763
0.37
0.37819
0.3763
0.42 e
0.09 i
0.30 o
0.07 u
"i"
2
"o"
"u"
Looking Ahead: Übung 7
2.1
Shannon/Fano Codierung
a) Applet
X
a
b
c
d
e
f
g
PX
0.10
0.15
0.34
0.17
0.05
0.09
0.10
b) Doing it by hand
X
a
b
PX
0.1
0.9
Berechne den Erwartungswert; Vergleiche Erwartungswert zur Entropie;
Berechne die Coderedundanz RC ,
RC = E[lC (X)] − H(X) ≥ 0
c) Quelle mit m = 2
X
aa
ab
ba
bb
PX
< T BD
< T BD
< T BD
< T BD
2
>
>
>
>
2.2
Arithmetische Codierung
a) ’aacbca’
• Ordne die Buchstaben lexikographisch (nicht nach den Wahrscheinlichkeiten)
• Fange mit 0 an → a ∈ [0, 12 ) . . .
b) Wort der Länge 10 mit 0.6 und dem Stellvertreter 0.63215699
c) Beweis... Zeige
h
⌊T̄ (x)⌋l(x) ∈ u(m) , o(m)
(1)
• good to know: ⌊T̄ (x)⌋l(x) < o(m) , da T̄ (x) < o(m)
2.3
Codierung der Ganzen Zahlen
In Prof. Maurers Skript, Seite 46ff...
• B(j) = Binäre Codierung von j
• L(j) = Länge von B(j) → L(j) = ⌊log j⌋ + 1
• C1 (j) = 0L(j)−1 kB(j)
• B(j) = 1kB ′ (j)
• C2 (j) = C1 (L(j))kB ′ (j)
n
C (j) =
C
n−1
0j−1 1
(L(j))kB ′ (j)
für n = 0
für n > 0
a) Tabelle für C1 und C2 von 1-10
j
1
...
B(j) L(j)
1
...
C1 (j)
...
C2 (j)
...
b) C2 ...
c) Modifiziere C2 so, dass er präfixfrei bleibt, aber alle W’keitsverteilungen
mit P (1) < P (2) + P (3) besser ist als C3 Ein paar Codewörter müssen
geändert werden...
2.4
Bedingte Entropie und Fehlerwahrscheinlichkeit
a) H(X|Y )
• H(X|X = j) =?
• H(X|Y ) =
N
P
...
j=1
• ...
3
b) numerisch: Untere Schranke der Fano-Ungleichung an die Fehlerwahrscheinlichkeit Pe bei N = 4 und N = 8.
c) Fehlerwahrscheinlichkeit bei der Schätzung von X: Bestmögliche Strategie?
• Gegeben Y = j → was ist die beste Strategie?
• Was ist dann die Erfolgswahrscheinlichkeit Ps ?
4