Aufgabe 1 Betrachten Sie im normativen Modell den Kauf eines

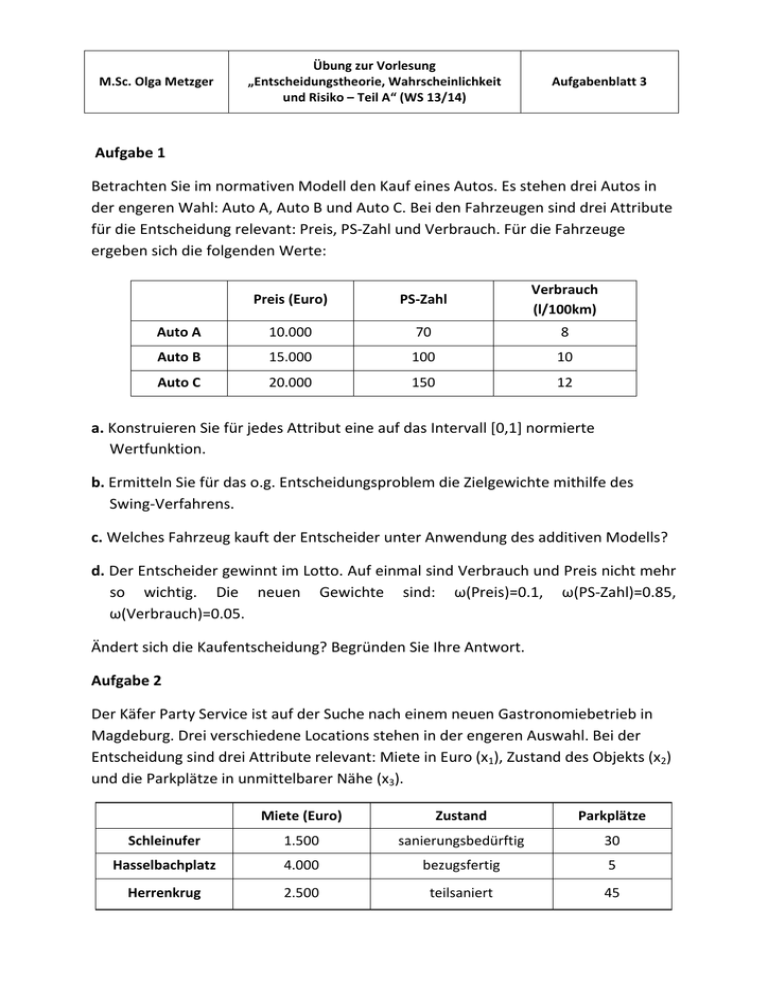
M.Sc. Olga Metzger Übung zur Vorlesung „Entscheidungstheorie, Wahrscheinlichkeit und Risiko – Teil A“ (WS 13/14) Aufgabenblatt 3 Aufgabe 1 Betrachten Sie im normativen Modell den Kauf eines Autos. Es stehen drei Autos in der engeren Wahl: Auto A, Auto B und Auto C. Bei den Fahrzeugen sind drei Attribute für die Entscheidung relevant: Preis, PS‐Zahl und Verbrauch. Für die Fahrzeuge ergeben sich die folgenden Werte: Preis (Euro) PS‐Zahl Verbrauch (l/100km) Auto A 10.000 70 8 Auto B 15.000 100 10 Auto C 20.000 150 12 a. Konstruieren Sie für jedes Attribut eine auf das Intervall [0,1] normierte Wertfunktion. b. Ermitteln Sie für das o.g. Entscheidungsproblem die Zielgewichte mithilfe des Swing‐Verfahrens. c. Welches Fahrzeug kauft der Entscheider unter Anwendung des additiven Modells? d. Der Entscheider gewinnt im Lotto. Auf einmal sind Verbrauch und Preis nicht mehr so wichtig. Die neuen Gewichte sind: ω(Preis)=0.1, ω(PS‐Zahl)=0.85, ω(Verbrauch)=0.05. Ändert sich die Kaufentscheidung? Begründen Sie Ihre Antwort. Aufgabe 2 Der Käfer Party Service ist auf der Suche nach einem neuen Gastronomiebetrieb in Magdeburg. Drei verschiedene Locations stehen in der engeren Auswahl. Bei der Entscheidung sind drei Attribute relevant: Miete in Euro (x1), Zustand des Objekts (x2) und die Parkplätze in unmittelbarer Nähe (x3). Miete (Euro) Zustand Parkplätze Schleinufer 1.500 sanierungsbedürftig 30 Hasselbachplatz 4.000 bezugsfertig 5 Herrenkrug 2.500 teilsaniert 45 Für den Käfer Party Service ist eine Location besser als die andere, wenn sie eine niedrigere Miete, einen besseren Zustand sowie mehr Parkmöglichkeiten hat. a. Ermitteln Sie unter Verwendung der Direct‐Rating‐Methode geeignete Wertefunktionen für die drei Attribute. Gehen Sie im Weiteren davon aus, dass der Käfer Party Service folgende Gewichte für die Attribute besitzt: ω1 = 0,1; ω 2 = 0,6 und ω3 = 0,3. b. Für welche Location entscheidet sich der Käfer Party Service? Aufgabe 3: Entscheidungen bei Ungewissheit Ein Entscheider steht vor dem Problem aus einer Menge von Investitionsalternativen (a1, a2, ..., a6) die beste Alternative auszuwählen. Zu welchem Erfolg eine Alternative führt, lässt sich im Zeitpunkt der Entscheidung nicht mit Sicherheit vorhersagen; dies ist abhängig von dem jeweils eintretenden Umweltzustand. Der Entscheider hält sechs Umweltzustände für möglich; deren Eintrittswahrscheinlichkeiten er jedoch nicht näher spezifizieren kann. Die Erfolge, die mit den Investitionsalternativen bei alternativen Umweltentwicklungen erzielt werden, enthält nachfolgende Tabelle: s1 s2 s3 s4 s5 s6 a1 2.000 2.500 5.000 500 ‐200 2.000 a2 1.500 3.000 ‐250 8.000 3.000 2.000 a3 1.400 2.500 300 1.000 800 2.100 a4 1.000 ‐800 900 600 2.100 500 a5 7.000 3.500 4.000 ‐100 1.600 900 a6 1.300 2.400 200 900 800 2.000 Welche Alternative wählt der Entscheider bei Anwendung a. der Maximin‐Regel? b. der Maximax‐Regel? c. des Hurwicz‐Prinzips (mit α =0,4)? d. der Niehans‐Savage‐Regel? e. der Laplace‐Regel?