Rechtwinklige Dreiecke

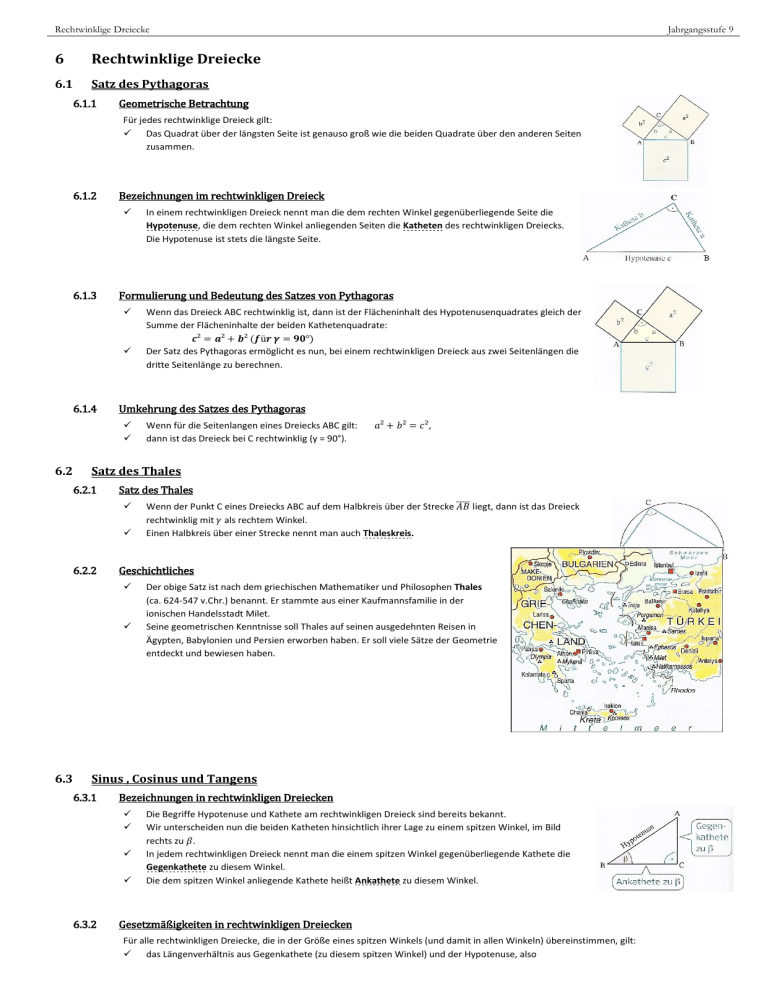
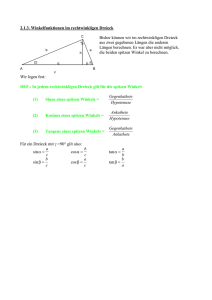
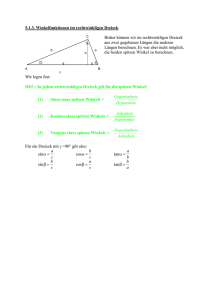
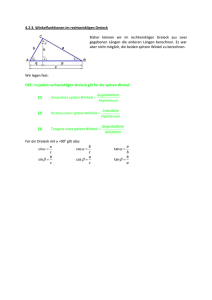
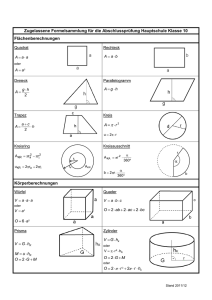
Rechtwinklige Dreiecke
6
Rechtwinklige Dreiecke
6.1
Satz des Pythagoras
6.1.1
Jahrgangsstufe 9
Geometrische Betrachtung
Für jedes rechtwinklige Dreieck gilt:
 Das Quadrat über der längsten Seite ist genauso groß wie die beiden Quadrate über den anderen Seiten
zusammen.
6.1.2
Bezeichnungen im rechtwinkligen Dreieck

6.1.3
6.1.4
Formulierung und Bedeutung des Satzes von Pythagoras

Wenn das Dreieck ABC rechtwinklig ist, dann ist der Flächeninhalt des Hypotenusenquadrates gleich der
Summe der Flächeninhalte der beiden Kathetenquadrate:

Der Satz des Pythagoras ermöglicht es nun, bei einem rechtwinkligen Dreieck aus zwei Seitenlängen die
dritte Seitenlänge zu berechnen.
Umkehrung des Satzes des Pythagoras


6.2
Wenn für die Seitenlangen eines Dreiecks ABC gilt:
dann ist das Dreieck bei C rechtwinklig (y = 90°).
,
Satz des Thales
6.2.1
Satz des Thales


6.2.2
Wenn der Punkt C eines Dreiecks ABC auf dem Halbkreis über der Strecke ̅̅̅̅ liegt, dann ist das Dreieck
rechtwinklig mit als rechtem Winkel.
Einen Halbkreis über einer Strecke nennt man auch Thaleskreis.
Geschichtliches


6.3
In einem rechtwinkligen Dreieck nennt man die dem rechten Winkel gegenüberliegende Seite die
Hypotenuse, die dem rechten Winkel anliegenden Seiten die Katheten des rechtwinkligen Dreiecks.
Die Hypotenuse ist stets die längste Seite.
Der obige Satz ist nach dem griechischen Mathematiker und Philosophen Thales
(ca. 624-547 v.Chr.) benannt. Er stammte aus einer Kaufmannsfamilie in der
ionischen Handelsstadt Milet.
Seine geometrischen Kenntnisse soll Thales auf seinen ausgedehnten Reisen in
Ägypten, Babylonien und Persien erworben haben. Er soll viele Sätze der Geometrie
entdeckt und bewiesen haben.
Sinus , Cosinus und Tangens
6.3.1
Bezeichnungen in rechtwinkligen Dreiecken




6.3.2
Die Begriffe Hypotenuse und Kathete am rechtwinkligen Dreieck sind bereits bekannt.
Wir unterscheiden nun die beiden Katheten hinsichtlich ihrer Lage zu einem spitzen Winkel, im Bild
rechts zu .
In jedem rechtwinkligen Dreieck nennt man die einem spitzen Winkel gegenüberliegende Kathete die
Gegenkathete zu diesem Winkel.
Die dem spitzen Winkel anliegende Kathete heißt Ankathete zu diesem Winkel.
Gesetzmäßigkeiten in rechtwinkligen Dreiecken
Für alle rechtwinkligen Dreiecke, die in der Größe eines spitzen Winkels (und damit in allen Winkeln) übereinstimmen, gilt:
 das Längenverhältnis aus Gegenkathete (zu diesem spitzen Winkel) und der Hypotenuse, also
Rechtwinklige Dreiecke
Jahrgangsstufe 9
hat immer den gleichen Wert.

das Längenverhältnis aus der Ankathete (zu diesem spitzen Winkel) und der Hypotenuse, also
hat immer den gleichen Wert.

das Längenverhältnis aus der Gegenkathete und der Ankathete (zu diesem spitzen Winkel), also
hat immer den gleichen Wert.

6.3.3
6.3.4
Diese Verhältnisse ändern sich nur, wenn der Winkel sich ändert. Sie bestimmen also den Winkel; deshalb gibt man ihnen eigene
Namen.
Der Sinus eines spitzen Winkels

Das Längenverhältnis aus der Gegenkathete zu einem spitzen Winkel und der Hypotenuse im rechtwinkligen
Dreieck nennt man den Sinus dieses Winkels:

Für das Dreieck ABC mit y = 90° gilt z. B.:
Der Kosinus eines spitzen Winkels

Das Längenverhältnis aus der Ankathete zu einem spitzen Winkel und der Hypotenuse im rechtwinkligen
Dreieck nennt man den Kosinus dieses Winkels:

Für das Dreieck ABC mit y = 90° gilt z. B.:
Rechtwinklige Dreiecke
6.3.5
6.3.6
Jahrgangsstufe 9
Der Tangens eines spitzen Winkels

Das Längenverhältnis aus Gegenkathete und Ankathete zu einem spitzen Winkel im rechtwinkligen Dreieck
nennt man den Tangens dieses Winkels:

Für das Dreieck ABC mit y = 90° gilt z. B.:
Bestimmen von Werten mit dem Taschenrechner
6.3.6.1
Bestimmen des Wertes zu vorgegebener Winkelgröße


6.3.6.2
Je nach Taschenrechner musst du erst die Winkelgröße eingeben und dann die Taste für z. B. Sinus drücken oder erst die Taste für
Sinus und dann die Winkelgröße eingeben. Probiere das bei deinem Taschenrechner am Beispiel sin 27° aus.
Achte darauf, dass der Taschenrechner DEG (von degree, engl. Grad) für die Winkelgröße anzeigt.
Als Ergebnis musst du 0,45399 ... erhalten.
Bestimmen der Winkelgröße zu vorgegebenem Wert




Die Tasten deines Taschenrechners sind doppelt belegt. Die Tasten sin cos und tan haben sin-1, cos-1 und tan-1 als zweite
Belegung.
Man erhält diese, indem man vorher die Taste 2nd (engl. second) drückt. sin-1 bedeutet: Man erhält umgekehrt zu einem
Sinuswert die zugehörige Winkelgröße.
Entsprechendes gilt für cos-1 und tan-1. Probiere das am Beispiel
zur Bestimmung von aus.
Als Ergebnis musst du 36,869 ...° erhalten.