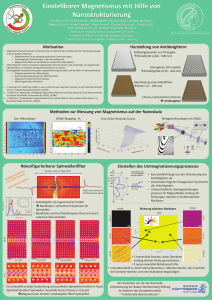
Phasenaufgelöste Untersuchung der Propagation von

Phasenaufgelöste Untersuchung der
Propagation von Spinwellenpaketen und der
Entstehung von Spinwellen–Kaustiken
Thomas Schneider
Dem Fachbereich Physik der Technischen Universität Kaiserslautern
zur Erlangung des akademischen Grades
Doktor der Naturwissenschaften“ eingereichte Dissertation
”
Betreuer: Prof. Dr. B. Hillebrands
Datum des Antrages auf Eröffnung des Promotionsverfahrens:
30.04.2009
Kurzfassung
Im Rahmen dieser Arbeit wurde die Anregung und Propagation von Spinwellenpaketen in magnetischen Filmen untersucht.
Für die hier vorgestellten Resultate wurde als magnetisches Material Yttrium–
Eisen–Granat (YIG) gewählt. Dieses erlaubt aufgrund seiner geringen Dämpfung
die Beobachtung der Spinwellenpropagation über Distanzen von einigen Millimetern und ist damit ideal für die Untersuchung mit Hilfe von orts-, zeit- und phasenaufgelöster Brillouin–Lichtstreuspektroskopie (BLS) geeignet. Die Anregung der
Spinwellen in diesem System kann leicht mit Mikrowellenpulsen geeigneter Frequenz (üblicherweise im GHz–Bereich) durchgeführt werden. Da die verwendeten
physikalischen Prinzipien nicht materialabhängig sind, können die grundsätzlichen
Resultate auch auf Spinwellen in anderen magnetischen Filmen übertragen werden.
Im ersten Teil dieser Arbeit wurde die Anregung und Propagation von Spinwellen in YIG–Wellenleitern untersucht. Dabei konnte dank der phasenaufgelösten BLS
erstmals direkt die Phasenänderung während der Propagation beobachtet werden.
Damit war es möglich, die Phasensymmetrie von gegenläufig propagierenden Spinwellen, die von derselben Mikrowellenantenne angeregt werden, zu untersuchen.
Es konnte gezeigt werden, dass diese genau wie die Amplitudensymmetrie von der
gewählten Geometrie, das heißt der Richtung der Propagation in Bezug auf das äußere Magnetfeld, abhängig ist. Propagieren die Spinwellen parallel zum magnetischen
Feld (die sogenannten “Backward–Volume–Moden”), haben die beiden gegenläufigen Wellen dieselbe Amplitude aber eine um π verschiedene Phase, während bei
der senkrecht zum Feld propagierenden “Surface–Mode” die Phasen gleich aber die
Amplituden deutlich verschieden sind. In weiteren Experimenten konnte durch die
Messung der Phasenänderung von nichtlinearen Spinwellenpulsen ein direkter Einfluss der Amplitude der Welle auf ihre Phase gezeigt werden.
Während bei der Propagation von Spinwellen in einem Wellenleiter parallel oder
senkrecht zum äußeren Feld die Gruppengeschwindigkeit parallel zum Wellenvektor ist, ist dies bei der unbeschränkten Ausbreitung im Allgemeinen nicht mehr der
Fall. Insbesondere führt das Vorhandensein einer durch das äußere Magnetfeld induzierten Anisotropie dazu, dass die Richtung der Gruppengeschwindigkeit für einen
weiten Bereich von Wellenvektorwinkeln unabhängig von diesem Winkel ist. Die-
ii
ser Effekt kann ausgenutzt werden, um ein lateral stabiles, lineares Wellenpaket anzuregen. Mit Hilfe verschiedener Wellenleiterantennen konnte in dieser Arbeit die
Anregung und Propagation dieser sogenannten Kaustiken experimentell untersucht
werden. Dabei wurde gezeigt, dass Existenz und Kontrast der Kaustiken abhängig
vom äußeren Feld und der verwendeten Anregungsstruktur sind; die erwartete Stabilität wurde für Propagationsdistanzen von über 10 mm nachgewiesen. Simulationen
der stationären Kaustiken bestätigen das beobachtete Verhalten. Die durchgeführten phasenaufgelösten BLS–Messungen zeigten, dass die laterale Ausdehnung nicht
durch die Wellenlänge der Kaustiken begrenzt ist. Aufgrund der anisotropen Ausbreitung der Spinwellen konnte die nicht–geometrische Reflexion der Kaustiken beobachtet werden. Weiter konnte die anisotrope Streuung an einem mechanischen
Defekt im YIG–Film gezeigt werden.
Eine mögliche Anwendung von Spinwellen in Form von Spinwellenlogik-Gattern wird im letzten Teil dieser Arbeit vorgestellt. Zur Realisierung der Gatter wird
ein Mach–Zehnder–Interferometer verwendet. Durch die lokale Änderung des magnetischen Felds durch das Oersted–Feld stromdurchflossener Leiter kann, abhängig
von Stärke und Ausdehnung dieser Änderung, die Amplitude oder die Phase der
Spinwelle im jeweiligen Interferometerarm und damit das Signal am Ausgang des
Interferometers geändert werden. Es konnte gezeigt werden, dass dieses Interferometer als logisches NOT, XNOR oder NAND Gatter verwendet werden kann, bei
dem die fließenden Ströme den logischen Eingängen und das Interferenzsignal dem
logischen Ausgang entspricht. Im Rahmen dieser Arbeit wurden funktionsfähige
Prototypen dieser Gatter aufgebaut und getestet. Dabei wurden verschiedene Realisierungen des Spinwelleninterferometers verwendet.
Abstract
In this thesis the excitation and propagation of spin–wave packets in magnetic films
have been studied.
For the results presented here yttrium iron garnet (YIG) was chosen as magnetic
material. Due to its small damping, YIG allows the observation of spin–wave propagation over distances of some millimeters, and is thus ideally suited for investigations
using space, time and phase resolved Brillouin light scattering spectroscopy (BLS).
The excitation of spin waves in this system can be done using microwave pulses of
suitable frequencies (typically in the GHz range). Since the used physical principles
are not material dependent, the general results can be transferred to spin waves in
other magnetic films.
In the first part of this thesis, the excitation and propagation of spin waves in
YIG waveguides were investigated. Using the phase–resolved BLS, the phase change
during propagation could be directly observed for the first time. Thus it was possible
to examine the phase symmetry of counterpropagating spin waves excited by the
same microwave antenna. It was shown that this symmetry, just like the amplitude
symmetry, depends on the selected geometry, i.e. the direction of the propagation
with respect to the external magnetic field. If the spin waves propagate parallel to
the magnetic field (Backward volume waves), the two waves moving in opposite
directions have the same amplitude but a phase difference of π . For surface waves
propagating perpendicular to the field, the phases are identical, while the amplitudes
are different. In further experiments, the direct influence of the amplitude of the
wave on its phase was shown by measuring the phase changes of nonlinear spin
wave pulses.
While the group velocity is parallel to the wave vector when the spin waves
propagate in a waveguide parallel or perpendicular to the external field, this is in
general not the case for an unrestricted propagation. In particular the presence of
anisotropy induced by the external magnetic field leads to the fact that the direction
of the group velocity for a wide range of wavevector angles is independent of that
angle. This effect can be used to excite a laterally stable, linear wave packet known as
caustic. With the help of different waveguide antennas the excitation and propagation
of these caustics were experimentally examined in this thesis. It was shown that
iv
existence and contrast of these caustics depend on the external field and the used
excitation structure; the expected stability was proven for propagation distances of
more than 10 mm. Simulations of the stationary caustics confirmed the observed
behaviour. The performed phase resolved BLS measurements showed that the lateral
expansion is not limited by the wavelength of the caustics. Due to the anisotropic
propagation of the spin waves the non–geometrical reflection of caustics could be
observed. Furthermore the anisotropic diffraction at a mechanical defect in the YIG
film was shown.
A possible application of spin waves in the form of spin waves logic gates is
presented in the last part of this thesis. To realize this gates a Mach–Zehnder–interferometer is used. By a local change of the magnetic field using the Oersted field
of a current–carrying conductor, depending on strength and width of this change,
the amplitude or the phase of the spin wave in the respective interferometer arm
and thus the signal in the exit of the interferometer is changed. It was shown that
this interferometer can be used as logical NOT, XNOR or NAND gates, where the
currents represent the logical inputs and the interference signal the logical output.
In this thesis working prototypes of these gates have been developed and tested.
Different implementations of the spin wave interferometer were demonstrated.
Inhaltsverzeichnis
1 Einleitung
2
3
Grundlagen der Spindynamik
2.1 Magnetische Wechselwirkungen . . . . . . . . . . . . . . . . . . .
2.1.1 Dipol–Dipol–Wechselwirkung und Streufeld . . . . . . . .
2.1.2 Austauschwechselwirkung . . . . . . . . . . . . . . . . . .
2.2 Landau–Lifschitz–Gleichung . . . . . . . . . . . . . . . . . . . . .
2.3 Polder–Suszeptibilitäts–Tensor . . . . . . . . . . . . . . . . . . . .
2.4 Spinwellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5 Dispersionsrelation für austauschdominierte Moden . . . . . . . . .
2.6 Dispersionsrelation dipolarer Moden in in–plane magnetisierten Filmen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.1 Walker–Gleichung . . . . . . . . . . . . . . . . . . . . . .
2.6.2 Allgemeine Dispersionsrelation dipolarer Spinwellen . . . .
2.6.3 Einfluss des dynamischen Streufelds auf die Richtung der
Gruppengeschwindigkeit . . . . . . . . . . . . . . . . . . .
2.6.4 Spezialfälle der Dispersionsrelation . . . . . . . . . . . . .
2.6.5 Wellenvektorabhängigkeit der Propagationsrichtung . . . .
1
5
5
5
7
8
10
12
12
14
14
15
20
21
22
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
3.1 Anregung und Detektion von Spinwellen durch Mikrowellenmesstechnik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Aufbau der Probe . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Brillouin–Lichtstreuspektroskopie . . . . . . . . . . . . . . . . . .
3.3.1 Brillouin–Lichtstreuprozess . . . . . . . . . . . . . . . . .
3.3.2 Experimenteller Aufbau . . . . . . . . . . . . . . . . . . .
3.3.3 Das Tandem–Fabry–Pérot–Interferometer . . . . . . . . . .
3.4 Orts- und zeitaufgelöste Brillouin–Lichtstreuspektroskopie . . . . .
25
25
27
30
30
32
32
35
vi
Inhaltsverzeichnis
3.5
4
Phasenaufgelöste Brillouin–Lichtstreuspektroskopie . . . . . . . . .
Phasenaufgelöste Untersuchung der Anregung und Propagation von Spinwellen in YIG–Wellenleitern
4.1 Propagation linearer Spinwellen . . . . . . . . . . . . . .
4.1.1 Phasenprofil einer linearen Spinwellen . . . . . . .
4.1.2 Lineare Phasenakkumulation . . . . . . . . . . . .
4.2 Phasensymmmetrie bei der Anregung von Spinwellen . . .
4.2.1 Phasensymmetrie von Backward–Volume–Wellen .
4.2.2 Phasensymmetrie von Surface–Wellen . . . . . . .
4.3 Einfluss der Nichtlinearität auf die Phase der Spinwellen .
4.3.1 Phasenprofil einer nichtlinearen Spinwelle . . . . .
4.3.2 Nichtlineare Phasenakkumulation . . . . . . . . .
5
36
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
5.1 Grundlagen der Kaustikanregung . . . . . . . . . . . . . . . . . .
5.1.1 Prinzip . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.2 Experimentelle Realisierung . . . . . . . . . . . . . . . .
5.1.3 Numerische Berechnung . . . . . . . . . . . . . . . . . .
5.1.4 Theoretische Beschreibung des Profils eines Kaustikstrahls
5.2 Kontrolle der Kaustikanregung durch externe Parameter . . . . . .
5.3 Kaustik–“Feinstruktur” . . . . . . . . . . . . . . . . . . . . . . .
5.4 Phasenstruktur von Spinwellen–Kaustikstrahlen . . . . . . . . . .
5.5 Reflexion und Streuung von Spinwellen–Kaustikstrahlen . . . . .
.
.
.
.
.
.
.
.
.
41
42
42
42
44
46
48
54
54
55
.
.
.
.
.
.
.
.
.
59
61
61
61
63
65
67
71
73
74
6
Spinwellenlogikgatter
6.1 Prinzip des Spinwelleninterferometers . . . . . . . . . . . . . . . .
6.1.1 Kontrolle der Phase von Spinwellen durch Ströme . . . . .
6.1.2 Kontrolle der Amplitude von Spinwellen durch Ströme . . .
6.2 Realisierung von XNOR–, NAND– und NOT–Spinwellenlogikgattern
6.2.1 XNOR–Gatter . . . . . . . . . . . . . . . . . . . . . . . .
6.2.2 NAND–Gatter . . . . . . . . . . . . . . . . . . . . . . . .
6.2.3 NOT–Gatter . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3 Spinwellenlogik mit einem Wellenleiter . . . . . . . . . . . . . . .
6.3.1 Interferometer auf einem Wellenleiter . . . . . . . . . . . .
6.3.2 Leistungsteiler auf einem Wellenleiter . . . . . . . . . . . .
77
78
79
81
82
82
84
85
86
86
89
7
Zusammenfassung und Ausblick
91
A Elektro–optischer Effekt
95
Inhaltsverzeichnis
vii
B Messung der Spinwellen–Phasenprofile
99
B.1 Berechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
B.2 Messung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
Eigene Veröffentlichungen
105
Literaturverzeichnis
107
Abkürzungsverzeichnis
γ
Gyromagnetisches Verhältnis
θ
Ausbreitungsrichtung der Spinwelle in Bezug auf das externe Magnetfeld
θK
Ausbreitungsrichtung des Spinwellen–Kaustikstrahls in Bezug auf
das externe Magnetfeld
κ
Nicht–Diagonalenkomponente des Polder–Suszeptibilitäts–Tensors
λ
Wellenlänge der Spinwelle
τ
Länge des Spinwellenpulses
φ
Richtung des in–plane–Wellenvektors in Bezug auf das externe
Magnetfeld
ϕ
Phase der Spinwelle
χ
Diagonalkomponente des Polder–Suszeptibilitäts–Tensors
χ̂
Polder–Suszeptibilitäts–Tensor
ω
Spinwellenfrequenz
Ak
Anregungsspektrum der Wellenleiterantenne
d
Filmdicke
h
Dynamisches Magnetfeld
hq
Magnetfeld der Mikrowellenantenne
hs
Dynamisches Streufeld
H0
Externes Magnetfeld
k
In–plane Wellenvektor der Spinwelle
k
Betrag des in–plane Wellenvektors der Spinwelle
ky
In–plane Wellenvektorkomponente senkrecht zum Feld
x
Abkürzungsverzeichnis
kz
In–plane Wellenvektorkomponente parallel zum Feld
m
Dynamische Magnetisierung
MS
Sättigungsmagnetisierung
q
Out–of–plane Wellenvektor der Spinwelle
w
Breite der Wellenleiterantenne
BLS
Brillouin–Lichtstreuspektroskopie
BVMSW
Backward Volume Magnetostatic Spin Waves
EOM
Elektro–optischer Modulator
MSSW
Magnetostatic Surface Spin Waves
NAND
Logisches Nicht–Und
NOT
Logisches Nicht
XNOR
Logisches Exklusiv–Nicht–Oder
YIG
Yttrium–Eisen–Granat
Kapitel 1
Einleitung
Die Untersuchung von Wellenphänomenen ist in nahezu allen Gebieten der Physik
von großer Bedeutung. Auch die Wellenanregungen magnetischer Systemen, die
sogenannten Spinwellen, die Thema dieser Arbeit sind, sind seit vielen Jahren Gegenstand verschiedenster Untersuchungen.
Seit der ersten experimentellen Beobachtung von Spinwellen in Yittrium–Eisen–
Granat (YIG) durch Eshbach [1, 2] waren dabei nicht nur grundlegende Fragestellungen der Spindynamik von Interesse. Da die Eigenschaften der Spinwellen stark
von einer Vielzahl von Materialparametern abhängen, kann die Messung des thermischen Spinwellenspektrums zur Bestimmung dieser Parameter verwendet werden.
Messungen dieser Art spielen heutzutage zum Beispiel eine wichtige Rolle bei der
Untersuchung von Heusler–Legierungen [3, 4].
Neben diesen thermischen Spinwellen ist auch die Untersuchung von künstlich
durch Mikrowellen angeregten Spinwellen von großer Bedeutung. In vielen Fällen,
unter anderem in dieser Arbeit, wird dabei YIG als Material verwendet, da dieses
dank seiner geringen Dämpfung die Propagation von Spinwellen über makroskopische Distanzen erlaubt. Aufgrund dieser Eigenschaft können Spinwellen in YIG in
vielfältiger Weise in Bauteilen zur analogen Signalverarbeitung bei Mikrowellenfrequenzen eingesetzt werden (siehe zum Beispiel [5, 6]).
Als weitere Anwendung von Spinwellen wurden in den letzten Jahren verschiedene Konzepte zur Realisierung von logischen Operation mit Hilfe von Spinwelleninterferometern vorgeschlagen [A1, A2, 7–11]. Das Konzept von Khitun et al. [8, 9]
verwendet die Spinwellen dabei nicht nur zur Durchführung der logischen Operationen, sondern auch zur Datenübermittlung zwischen den einzelnen Logikgattern. Vom selben Autor stammt auch ein Modell zur Verwendung von Spinwellen in
Quantencomputern [12].
Da für eine kommerzielle Anwendung von Spinwellenlogikgattern die Größe der
resultierenden Bauteile von entscheidender Bedeutung ist, basieren die meisten die-
2
Einleitung
ser Konzepte auf Permalloy, da dieses Material deutlich kleinere Strukturen als YIG
erlaubt. Die zugrundeliegende Physik entspricht im Wesentlichen der in YIG, so
dass die dort gewonnenen Erkenntnisse meist problemlos übertragen werden können.
Die Möglichkeit Spinwellen in kleineren (dass heißt Mikrometergroßen) Strukturen anzuregen und zu beobachten ermöglicht auch die Untersuchung neuer Effekte, wie zum Beispiel die Wechselwirkung von Spinwellen mit Domänenwänden
[7, 13, 14] oder mit spinpolarisierten Strömen (Spin torque transfer) [15–21]; betrachtet man strukturiertes Permalloy können die Einflüsse von Quantisierungen oder
Inhomogenitäten im internen Magnetfeld auf das Spinwellenspektrum beobachtet
werden [22–24]. Wie kürzlich gezeigt wurde, ermöglicht Permalloy auch den Aufbau und die Untersuchung von dreidimensionalen Strukturen, zum Beispiel einer
Röhre [25]
Der Einfluss einer Strukturierung des magnetischen Materials auf die Propagation von Spinwellen konnte kürzlich anhand der Realisierung eines eindimensionalen
magnonischen Kristalls, bestehend aus einer regelmäßigen Anordnung von Gräben,
untersucht werden [26]. Die Transmissionscharakteristik dieser Struktur wird dabei
durch Interferenz zwischen den an den Gräben reflektierten Wellen bestimmt. Eine genaue Kenntnis der Phaseneigenschaften von Spinwellen und insbesondere der
Einflüsse die hohe Spinwellenintensitäten und der Anregungsprozess auf die Phase
haben ist daher von besonderer Bedeutung zum Verständnis dieses magnonischen
Kristalls. Weitere Möglichkeiten zur Herstellung eines magnonischen Kristalls werden zum Beispiel in [27–31] vorgestellt.
Nicht vergessen werden sollte, dass Spinwellen in YIG auch als Modellsystem
für andere physikalische Fragestellungen verwendet werden können. Zum Beispiel
werden schon seit vielen Jahren nichtlineare Wellenphänomene, wie sie auch in der
Optik auftreten, an Spinwellen in YIG untersucht [32–39]. Vorteil hierbei ist nicht
nur, dass die Nichtlinearität eine inhärente Eigenschaft der Spinwelle ist und damit nicht Materialabhängig ist, sondern auch, dass Spinwellen vergleichsweise langsam propagieren. Damit ist es möglich die Ausbildung nichtlinearer Effekte zeitaufgelöst zu beobachten. Beachtet man weiter, dass mit der orts-, zeit- und phasenaufgelösten Brillouin–Lichtstreuspektroskopie (BLS) ein vielseitiges Beobachtungsinstrument zur Verfügung steht und das durch die Kontrolle des externen Magnetfelds
die Wellenlänge der Spinwelle quasi unabhängig von der Spinwellenfrequenz eingestellt werden kann, wird klar, welchen Vorteil die Untersuchung der nichtlinearen
Spinwellenoptik gegenüber der “klassischen” nichtlinearen Optik hat.
Dabei konnten nicht nur die aus der Optik bekannten hellen und dunklen Solitonen [40] in Spinwellenwellenleitern beobachtet werden, sondern auch eine neuartige, symmetriebrechende Form einer nichtlinearen Anregung in einer Ringstruktur
erzeugt und untersucht werden. Dieses sogenannte “Moebius–Soliton” ändert bei
jedem Umlauf seine Phase um π und muss daher den Ring zweimal umlaufen, bevor
es den Ausgangsort wieder mit der gleichen Phase erreicht [41, 42].
Einleitung
Betrachtet man die quantenmechanischen Teilcheneigenschaften von Spinwellen, dass heißt wechselt man zum Bild der Magnonen, können Spinwellen in YIG
als Modellsystem für wechselwirkende bosonische Gase verwendet werden. Ein
eindrucksvolles Beispiel hierfür ist die kürzlich von Demokritov et al. realisierte Bose–Einstein–Kondensation von Magnonen bei Zimmertemperatur [43]. Die
BLS ermöglicht auch in diesem Fall die zeitaufgelöste Untersuchung der kollektiven Dynamik dieses sogenannten Magnonengases. Mit dem parametrischen Pumpen [44–51] steht dabei ein wirkungsvolles Werkzeug zur Manipulation des Magnonengases zur Verfügung. Zu beachten ist, dass die parametrischen Prozesse phasensensitiv sind [A4, 52], so das auch hier eine genaue Kenntnis der Spinwellenphase
von großer Bedeutung ist.
Bisher unerwähnt blieb die Tatsache, dass die Propagation von Spinwellen stark
anisotrop ist. Ursache hierfür ist, dass durch die Richtung des externe Magnetfelds
eine ausgezeichnete Richtung im Propagationsmedium existiert. Diese Anisotropie
führt unter anderem dazu, dass die Ausbreitungsrichtung der Spinwelle im Allgemeinen nicht parallel zur Richtung ihres Wellenvektors ist. Insbesondere ist die
Beziehung zwischen diesen beiden Richtungen nicht monoton und es existiert ein
Bereich von Wellenvektorrichtungen in dem die Richtung der Gruppengeschwindigkeit unabhängig von der des Wellenvektors ist. Dies ermöglicht bei einem geeigneten Anregungsspektrums die eigenständige Ausbildung stabiler, lateral begrenzter
Spinwellenstrahlen, sogenannter Kaustiken [53, 54].
Die im Rahmen dieser Arbeit behandelten Themen, sind mit den meisten der
bisher diskutierten Fragestellungen verknüpft. So behandelt ein Teil dieser Arbeit,
die Phaseneigenschaften von Spinwellen in YIG. Außerdem wird die Anregung und
Kontrolle von Spinwellen–Kaustiken untersucht. Im Bereich der Anwendungen von
Spinwellen wird ein Konzept von Spinwellenlogikgattern getestet.
Im Einzelnen gliedert sich die Arbeit wie folgt: Zunächst werden in Kapitel 2 die
notwendigen theoretischen Grundlagen zum Verständnis dieser Arbeit vorgestellt.
Den Hauptteil dieses Kapitels bildet dabei die Herleitung der Dispersionsrelation
dipolarer Spinwellen und die Besprechung ihrer Eigenschaften.
Anschließend werden in Kapitel 3 die verwendeten Methoden zur Anregung und
Untersuchung der Spinwellen vorgestellt. Nach einem kurzen Überblick über die
verwendete Mikrowellentechnik folgt eine ausführliche Diskussion der BLS Technik
und des verwendeten Aufbaus. Insbesondere wird dabei auf die Realisierung der
orts-, zeit- und phasenaufgelösten BLS eingegangen.
In den anschließenden Kapiteln werden die im Rahmen dieser Arbeit gewonnenen Resultate vorgestellt. Kapitel 4 behandelt die phasenaufgelöste Untersuchung
der Propagation und Anregung linearer und nichtlinearer Spinwellen. Die dazu verwendete Technik — die Messung der Phasenänderung mit der Propagationsdistanz
der Spinwelle, die sogenannte Phasenakkumulation — wird zunächst am einfachen
Fall einer linearen Spinwelle vorgestellt. Anschließend wird diese Methode verwen-
3
4
Einleitung
det, um die Phasensymmetrie bei der Anregung von Spinwellen in verschiedenen
Geometrien zu bestimmen. Das Kapitel endet mit der Untersuchung der Phasenakkumulation einer nichtlinearen Spinwelle und des Einflusses der Spinwellenamplitude auf die Spinwellenphase.
In Kapitel 5 wird die Untersuchung der Anregung und Propagation der bereits
erwähnten Spinwellen–Kaustiken behandelt. Zunächst wird das Prinzip der Anregung diskutiert und eine Antennenstruktur vorgestellt, die die kontrolierte Anregung
von Spinwellen–Kaustiken ermöglicht. Verschiedene Möglichkeiten der Beeinflussung der Anregung werden vorgestellt; die gewonnen Resultate werden mit numerischen und analytischen Modellen verglichen. Weiter wird die Phasenstruktur der
Kaustiken untersucht, so wie der Einfluss der induzierten Anisotropie auf die Reflexion und Streuung von Spinwellen–Kaustiken besprochen.
In Kapitel 6 wird eine Realisierung von Spinwellenlogik untersucht. Zur Umsetzung der logischen Operationen wird dabei gezielt die Phase oder die Amplitude
der Spinwellen in den beiden Armen des Interferometers beeinflusst. Auf YIG basierende Prototypen verschiedener Logikgatter werden getestet. Abschließend wird
eine verbesserte Realisierung eines Spinwelleninterferometers vorgestellt.
Die Arbeit schließt mit einer Zusammenfassung der gewonnenen Erkenntnisse
und einem kurzen Ausblick auf weitere mögliche Untersuchungen.
Kapitel 2
Grundlagen der Spindynamik
Im Folgenden sollen die notwendigen theoretischen Grundlagen, die zum Verständnis dieser Arbeit benötigt werden, zusammengefasst werden. Dazu wird zunächst
kurz auf die magnetischen Wechselwirkungen eingegangen (Kapitel 2.1), bevor mit
der Landau–Lifschitz–Gleichung (Kapitel 2.2) und der daraus abgeleiteten Polder–
Suszeptibilität (Kapitel 2.3) die notwendigen Grundgleichungen der Spindynamik
besprochen werden. Davon ausgehend wird nach einem kurzen Überblick über die
allgemeinen Eigenschaften von Spinwellen (Kapitel 2.4) zunächst die Dispersionsrelation austauschdominierter Spinwellen behandelt (Kapitel 2.5), bevor dann die
Dipsersionsrelation für die im Rahmen dieser Arbeit untersuchten dipolaren Spinwellen hergeleitet wird (Kapitel 2.6). Für einen umfangreicheren Überblick über die
Physik des Magnetismus sei auf [55, 56] verwiesen. Weiterführende Darstellungen
zur Spindynamik finden sich unter anderem in [57–59].
Alle Rechnungen werden im Gauß–System durchgeführt. Eine Umrechnungstabelle in das SI–System findet man zum Beispiel in [60].
2.1 Magnetische Wechselwirkungen
2.1.1 Dipol–Dipol–Wechselwirkung und Streufeld
Die Wechselwirkungsenergie zwischen zwei Dipolen µi und µ j im Abstand ri j beträgt [61]
"
#
µi · µ j
(µi · ri j )(µ j · ri j )
E(µi , µ j , ri j ) =
−3
.
(2.1)
ri3j
ri5j
Die Dipol–Dipol–Wechselwirkung ist (im Vergleich zur Austauschwechselwirkung,
siehe Kapitel 2.1.2) langreichweitig, so dass für die Energie E(µi ) eines Dipols µi
6
Grundlagen der Spindynamik
der Beitrag aller Atome in einem Festkörper berücksichtigt werden muss
E(µi ) = ∑ E(µi , µ j , ri j ) .
(2.2)
j
Um die Größenordnung der Wechselwirkungsenergie abschätzen zu können, ist es
allerdings ausreichend, zwei Momente µ = µB im Abstand von zwei Bohr’schen
Radien a0 zu betrachten. Man erhält in diesem Fall für die Wechselwirkungsenergie der Dipole E ≈ 0,6 meV. Diese Energie entspricht einer thermischen Energie
von etwa 7 K. Vergleicht man diese Temperatur mit der Curie–Temperatur typischer
Ferromagnete (Fe: 1043 K, Ni: 627 K, Co: 1388 K [62]), ist offensichtlich, dass die
Dipol–Dipol–Wechselwirkung nicht die Ursache für die ferromagnetische Ordnung
sein kann.
Wie die folgende Überlegung zeigt, spielen die Dipolmomente trotzdem eine
wichtige Rolle. Statische magnetische Momente im Inneren eines Festkörpers werden in vielen Fällen (z.B. bei kubischer Kristallstruktur) kompensiert und liefern
keinen Beitrag zur Dipolenergie. An der Oberfläche existieren allerdings unkompensierte Momente, die das sogenannte Streufeld oder Entmagnetisierungsfeld Hs
erzeugen.
Zur Berechnung dieses Streufeldes verwendet man die magnetostatischen Maxwellgleichungen
∇ × Hs = 0
∇ · B = ∇ · (Hs + 4πM ) = 0 .
(2.3)
(2.4)
Gleichung (2.3) erlaubt wegen ∇×(∇Ψ ) = 0 die Definition eines skalaren Potentials
ψ mit Hs = −∇ψ . Einsetzen in Gl. (2.4) liefert
∆ψ = 4π∇ · M = −ρM
.
(2.5)
Dieser Ausdruck entspricht der aus der Elektrostatik bekannten Poisson–Gleichung
mit einer magnetischen Ladungsdichte ρM = −4π∇·M , daher können die Lösungen
übernommen werden [61].
Für einen homogen magnetisierten Ellipsoid erhält man so eine lineare Beziehung zwischen Magnetisierung M und Streufeld Hs . Diese kann in der Form
Hs = −4πN̂ M
(2.6)
geschrieben werden. Der symmetrische Tensor N̂ heißt Entmagnetisierungstensor;
seine Komponenten sind nicht ortsabhängig. Im Hauptachsensystem des Ellipsoiden
ist er diagonal, die Spur ist Eins. Diese Diagonalelemente sind für einige Körper in
Tab. 2.1 angegeben.
2.1 Magnetische Wechselwirkungen
Kugel
Zylinder k ez
Film in (y, z)–Ebene
7
Nxx
Nyy
Nzz
1
3
1
2
1
3
1
2
1
3
0
1
0
0
Tabelle 2.1: Diagonalelemente des Entmagnetisierungstensors N̂ für verschiedene ellipsoide Körper [63].
Für die weitere Betrachtung ist insbesondere wichtig, dass im Fall eines (unendlich ausgedehnten) in–plane magnetisierten Films kein (statisches) Streufeld Hs
auftritt. Da allerdings die dynamische Magnetisierung m (siehe Kapitel 2.3) out–
of–plane Komponenten besitzt, tritt ein dynamisches Streufeld hs auf, das berücksichtigt werden muss (zur Definition von statischer und dynamischer Magnetisierung
siehe Kapitel 2.3).
2.1.2 Austauschwechselwirkung
Wie in Kapitel 2.1.1 begründet wurde, kann die Dipol–Dipol–Wechselwirkung nicht
die Ursache für die ferromagnetische Ordnung sein. Diese Ordnung lässt sich nur
erklären, wenn man die quantenmechanische Austauschwechselwirkung berücksichtigt [55,56]. Diese wurde erstmals von Heisenberg behandelt [64]. Die wesentlichen
Überlegungen dazu werden im Folgenden wiedergegeben.
Elektronen sind Fermionen, das heißt, die Wellenfunktion eines Mehrelektronensystems muss antisymmetrisch unter Vertauschung zweier Teilchen sein (Pauli–
Prinzip) [65]. Betrachtet man ein Zwei–Elektronen–System, so sind deshalb nur
Kombinationen aus einer symmetrischen Spinwellenfunktion (parallele Spins) mit
einer antisymmetrischen Ortswellenfunktion oder umgekehrt möglich.
Diese beiden Möglichkeiten führen zu verschiedenen Aufenthaltswahrscheinlichkeiten für die Elektronen und damit zu verschiedenen Energieeigenwerten. Die
Differenz zwischen diesen Energien nennt man Austauschenergie Eex .
Der Hamilton–Operator Ĥ für die Austauschwechselwirkung zwischen zwei
Spins Ŝ1 und Ŝ2 kann in der Form
Ĥ = −Eex
1
1
Ŝ · Ŝ2 = −2J 2 Ŝ1 · Ŝ2
2 1
h̄
h̄
(2.7)
geschrieben werden. Ŝ1 und Ŝ2 sind die Spinoperatoren. Die Kopplungskonstante
J, das so genannte Austauschintegral, kann beide Vorzeichen annehmen. Ist sie positiv, sind parallele Spins energetisch günstiger; man spricht von “Ferromagnetischer
8
Grundlagen der Spindynamik
Kopplung”. Im umgekehrten Fall stellen sich die Spins bevorzugt antiparallel, es
ergibt sich die “Antiferromagnetische Kopplung” [56].
Für einen Festkörper mit N Spins kann der Hamilton–Operator der Austauschwechselwirkung als Näherung durch die Summation über die Zwei–Spin–Wechselwirkung zwischen allen Paaren von Spins beschrieben werden. Man erhält
1
Ĥ = − 2
h̄
N
∑ ∑
j=1
l
(l6= j)
J j,l Ŝ j · Ŝl
.
(2.8)
Quantenmechanische Rechnungen zeigen, dass das Austauschintegral mit Hilfe
der Ein–Elektronen–Wellenfunktionen ϕ j,l (r) als
J j,l = 2
Z
ϕl∗ (r1 )ϕ ∗j (r2 )
e2
ϕl (r2 )ϕ j (r1)dr1 dr2
|r1 − r2 |
(2.9)
dargestellt werden kann (e ist dabei die Elementarladung) [56]. Aus dieser Gleichung ergibt sich, dass J j,l nur dann von Null verschieden sein kann, wenn die Wellenfunktionen ϕ j,l überlappen. Da ein nennenswerter Überlapp nur bei nahe benachbarten Atomen auftritt, ist die Austauschwechselwirkung kurzreichweitig. In vielen
Fällen reicht es daher aus, nur die Wechselwirkung zwischen nächsten Nachbarn zu
betrachten und die Summation über l in Gl. (2.8) entsprechend zu beschränken.
2.2 Landau–Lifschitz–Gleichung
Die Landau–Lifschitz–Gleichung beschreibt phänomenologisch die Bewegung der
Magnetisierung in einem magnetischen Feld und bildet somit die Grundlage aller
weiteren Betrachtungen zur Spindynamik. Sie soll im Folgenden hergeleitet werden
(siehe auch [63]).
Auf ein magnetisches Moment µ in einem Magnetfeld H wirkt ein Drehmoment
T = µ×H
.
(2.10)
Das magnetische Moment µ ist mit dem Drehimpuls L durch das gyromagnetische Verhältnis γ verknüpft
µ
L=−
.
(2.11)
|γ |
Mit Gl. (2.10) erhält man daraus
µ×H = T =
dL
1 dµ
=−
dt
|γ | dt
.
(2.12)
2.2 Landau–Lifschitz–Gleichung
Heff
− |γ | M × Heff
M
9
Abbildung 2.1: Bewegung der Magnetisierung M in einem Magnetfeld Heff . Aufgrund
des wirkenden Drehmoments präzediert die
Magnetisierung um das effektive Feld Heff
(durchgezogene Linie). In realen Medien wird
die Amplitude der Präzession gedämpft, bis
die Magnetisierung schließlich parallel zum
Feld liegt (gestrichelte Linie).
Ein magnetisches Moment, das nicht parallel zum Feld ausgerichtet ist, präzediert also um die Feldrichtung. In realen Medien wird diese Präzession gedämpft, so
dass sich das Moment nach einiger Zeit parallel zum Feld einstellt.
Der Übergang zur Magnetisierung M liefert die Landau–Lifschitz–Gleichung
[66]
dM
= − |γ | M × Heff .
(2.13)
dt
Heff ist dabei das effektive Feld, das auf die Magnetisierung wirkt. Zu diesem effektiven Feld tragen neben dem konstanten und dem zeitabhängigen äußeren Feld H0
und H(t) (z.B. das Feld des anregenden Mikrowellensignals, vgl. Kapitel 3.1) auch
das Anisotropie- und das Austauschfeld Hani und Hex [24] sowie das statische und
das dynamische Streufeld Hs und hs (t) (vgl. Kapitel 2.1.1 und 2.3) bei
Heff = H0 + H(t) + Hani + Hex + Hs + hs (t) .
(2.14)
Wie bereits in Kapitel 2.1.1 erwähnt, werden in dieser Arbeit nur in–plane magnetisierte Filme betrachtet, so dass kein statisches Streufeld Hs auftritt. Weiter können
aufgrund der geringen kristallographischen Anisotropie des verwendeten Materials
(Yittrium Eisen Granat, siehe Kapitel 3.2) und der Beschränkung auf dipolare Spinwellen (Kapitel 2.4) Anisotropie- und Austauschfeld vernachlässigt werden, so dass
sich Gl. (2.14) auf
Heff = H0 + H(t) + hs(t)
(2.15)
reduziert.
Da das dynamische Streufeld hs (t) eine Funktion der Magnetisierung ist (vgl.
Gl. (2.6)), ist die Landau–Lifschitz–Gleichung (2.13) und damit alle von ihr abgeleiteten Dispersionrelationen intrinsisch nichtlinear. Da im Folgenden allerdings nur
kleine Auslenkungen aus der Ruhelage betrachtet werden, kann diese Nichtlinearität
vernachlässigt werden.
10
Grundlagen der Spindynamik
Dämpfungsprozesse können durch das Einfügen eines phänomenologischen Zusatzterms berücksichtigt werden. Landau und Lifschitz schlugen dazu eine Erweiterung von Gl. (2.13) der Form
dM
λ |γ |
= − |γ | M × Heff −
M × (M × Heff )
dt
|M |
(2.16)
α
dM
dM
= − |γ | M × Heff −
M×
dt
|M |
dt
(2.17)
vor [66]. λ ist dabei ein dimensionsloser Dämpfungsparameter. Dieser Ansatz kann
allerdings nur für kleine λ verwendet werden, da die Stärke des Dämpfungsterms
mit λ ohne Beschränkung steigt. Damit würde die Zeit zum Erreichen der Ruhelage
(M k Heff ) mit steigender Dämpfung abnehmen [67]. Dieses Verhalten widerspricht
jedoch allen Beobachtungen.
Ein von Gilbert vorgeschlagener alternativer Ansatz hat die Form
und behebt dieses Problem, da die Dämpfung hier proportional zur Änderung der
Magnetisierung ist [68]. Im Fall kleiner Dämpfung (α ≪ 1, λ ≪ 1) ist er äquivalent
zu Gl. (2.16).
Die Dämpfung steht in beiden Fällen senkrecht zur Magnetisierung und ändert
daher den Betrag von M nicht, wie durch Multiplikation von Gl. (2.16) und (2.17)
mit M und unter Berücksichtigung von
M
1d
dM
=
M2
dt
2 dt
gezeigt werden kann.
2.3 Polder–Suszeptibilitäts–Tensor
Die Landau–Lifschitz–Gleichung (2.13) lässt sich im Fall kleiner Auslenkungen aus
der Ruhelage und unter Vernachlässigung der Dämpfung zu einer linearen Beziehung zwischen den dynamischen Anteilen des magnetischen Feldes umformen. Dazu wird angenommen, dass sich Heff (t) und M (t) in der Form
M (t) = M0 + m(t)
Heff (t) = H0 + h(t) ,
(2.18)
mit
m(t) = me−iω t
−iω t
h(t) = he
, |m| ≪ |M0 |
,
|h| ≪ |H0 |
(2.19)
2.3 Polder–Suszeptibilitäts–Tensor
11
schreiben lassen. Ein zeitabhängiges äußeres Feld H(t) tritt im Rahmen dieser Arbeit nur als Feld des anregenden Mikrowellensignals H(t) = hq e−iω t auf und kann
daher gegebenenfalls in h(t) berücksichtigt werden. Weiter soll gelten
H0 = H0 ez
, M0 = MS ez
.
(2.20)
Dies entspricht einem magnetisch gesättigten Ein–Domänen–Zustand ohne Anisotropie, also zum Beispiel einem eindomänigen, in–plane magnetisierten Film. MS ist
die Sättigungsmagnetisierung; Feld und Magnetisierung sind in z–Richtung orientiert. Für kleine Auslenkungen aus dem Gleichgewicht bleiben die z–Komponenten
von H(t) und M (t) unverändert, das heißt, m und h haben nur Komponenten in x–
und y–Richtung




mx (t)
hx (t)
m(t) = my (t) , h(t) = hy (t) .
(2.21)
0
0
Einsetzen von Gl. (2.18) in die Landau–Lifschitz–Gleichung (2.13) liefert
h
i
dm(t)
= −|γ | M0 × H0 + M0 × h(t) + m(t) × H0 + m(t) × h(t) . (2.22)
dt
Der erste Term in der Klammer ergibt Null (H0 k M0 ); der letzte Term kann als
Produkt zweier vom Betrag her kleiner Größen vernachlässigt werden. Einsetzen
von Gl. (2.19) und (2.20) liefert
iω m(t) = |γ |ez × [MS h(t) − H0m(t)]
.
(2.23)
Bringt man Gl. (2.23) in die Form m(t) = χ̂h(t), so erhält man


χ −iκ 0
1 
χ̂ =
i κ χ 0
4π
0
0 0
(2.24)
mit
und
χ=
ωH ωM
ωH2 − ω 2
ωM = |γ |4πMS
, κ=
ω ωM
ωH2 − ω 2
, ωH = |γ |H0
(2.25)
.
(2.26)
χ̂ heißt Polder–Suszeptibilitäts–Tensor [58].
Wie in [57] gezeigt wird kann die Dämpfung leicht durch die Einführung einer
komplexen Frequenz erreicht werden. Dazu muss nur in den Ausdrücken für χ und κ
(Gl. (2.25)) die Frequenz ωH durch ωH +iαω mit dem Gilbert Dämpfungsparameter
α (siehe Gl. (2.17)) ersetzt werden.
12
Grundlagen der Spindynamik
2.4 Spinwellen
Betrachtet man ein magnetisches Moment, das durch eine Störung aus der Ruhelage
ausgelenkt wurde, beschreibt die Landau–Lifschitz–Gleichung (2.13) die Präzession
dieses Momentes um die Richtung der Magnetisierung. Das Moment koppelt dabei
durch die Dipol–Dipol– und die Austauschwechselwirkung (vgl. Kapitel 2.1) an die
benachbarten Momente. Die Störung breitet sich daher als Welle im Festkörper —
oder genauer — im Spinsystem des Festkörpers aus. Man spricht von Spinwellen
oder, in der Sprache der zweiten Quantisierung, von Magnonen.
Da der Betrag des magnetischen Momentes aufgrund der starken Austauschwechselwirkung konstant bleiben muss, haben Spinwellen nur zwei Freiheitsgrade [63].
Bei der theoretischen Beschreibung von Spinwellen ist zu beachten, dass sich die
beiden Wechselwirkungen sowohl in Stärke als auch in Reichweite deutlich voneinander unterscheiden. Daher muss abhängig von der Wellenlänge λ der betrachteten
Spinwelle in vielen Fällen nur eine der Wechselwirkungen berücksichtigt werden.
Ist die Wellenlänge klein, so ist die Austauschwechselwirkung zwischen benachbarten Spins groß, da diese stark gegeneinander verkippt sind. Die schwache dipolare Wechselwirkung kann daher vernachlässigt werden, man spricht von austauschdominierten Moden (vgl. Kapitel 2.5).
Für Spinwellen mit großer Wellenlänge und geringer Amplitudenvariation über
die Filmdicke (wie sie im Rahmen dieser Arbeit untersucht werden) ist die Verkippung zwischen benachbarten Spins sehr gering, die Austauschwechselwirkung ist
schwach und kann gegenüber der dipolaren Wechselwirkung vernachlässigt werden.
Man spricht daher auch von dipolaren Moden. Diese werden in Kapitel 2.6 behandelt.
2.5 Dispersionsrelation für austauschdominierte
Moden
Die Spinoperatoren in Gl. (2.8) können durch die Pauli–Spinmatrizen
h̄ 0 1
Ŝ =
2 1 0
x
h̄ 0 −i
Ŝ =
2 i 0
y
h̄ 1 0
Ŝ =
2 0 −1
z
(2.27)
dargestellt werden [65]. Anstelle der Operatoren Ŝx und Ŝy ist es günstiger, die Spinumklappoperatoren
Ŝ± = Ŝx ± iŜy
(2.28)
2.5 Dispersionsrelation für austauschdominierte Moden
13
zu verwenden. Die Spineigenzustände werden durch
1
0
|↑i =
|↓i =
0
1
(2.29)
dargestellt. Die Wirkung der Operatoren auf diese Zustände ist
Ŝ+ |↑i = 0
Ŝ+ |↓i = |↑i
Ŝ− |↑i = |↓i
Ŝ− |↓i = 0
(2.30)
und
1
Ŝz |↑i = |↑i
2
1
Ŝz|↓i = − |↓i .
2
(2.31)
Mit diesen Operatoren lässt sich der Austausch–Hamilton–Operator für N Spins
(2.8) als
1 + −
J N
z z
− +
Ŝ Ŝ + Ŝ j Ŝδ
(2.32)
Ĥ = − 2 ∑ ∑ Ŝ j Ŝδ +
2 j δ
h̄ j=1 δ =NN
darstellen. Dabei werden aufgrund der kurzen Reichweite der Austauschwechselwirkung bei der zweiten Summation nur die z Nächsten Nachbarn von j berücksichtigt
(vgl. Kapitel 2.1.2).
Der Grundzustand dieses Operators kann in der Basis der Spineigenzustände
durch
|0i = ∏ |↑il
(2.33)
l
beschrieben werden. Ein Zustand, in dem nur einer der Spins umgeklappt ist, wie
− |0i, ist kein Eigenzustand von Gl. (2.32), da der Operator
zum Beispiel |↓m i = Ŝm
−
+ Ŝ diesen Spin an den Ort k verschiebt und damit einen neuen Zustand erzeugen
Ŝm
k
würde. Bildet man allerdings eine Linearkombination aus allen |↓m i
1
|ki = √ ∑ eik·rm |↓m i ,
N m
(2.34)
erhält man einen Eigenzustand von Gl. (2.32) [69]. Der Zustand |ki beschreibt dabei
eine Spinwelle mit Wellenvektor k. Die Energieeigenwerte von |ki können mit Hilfe
der stationären Schrödinger–Gleichung Ĥ|ki = E|ki berechnet werden. Man erhält
!
1 z ik·rδ
E = E0 + J z − ∑ e
+ e−ik·rδ
2 δ
!
z
= E0 + J z − ∑ cos (k · rδ )
δ
.
(2.35)
14
Grundlagen der Spindynamik
Für nicht zu große Wellenvektoren k kann der Ausdruck entwickelt werden. Man
erhält
1 z
(2.36)
E ≈ E0 + J ∑(k · rδ )2 .
2 δ
Mit E = h̄ω ergibt sich damit für die Dispersion von austauschdominierten Spinwellen
ω ∼ k2 .
(2.37)
2.6 Dispersionsrelation dipolarer Moden in in–plane
magnetisierten Filmen
Dispersionsrelation dipolarer Moden in isotropen1 , in–plane magnetisierten Filmen
wird hier im wesentlichen der Ansatz von Damon und Eshbach [71, 72] beziehungsweise die Formulierung von Hurben und Patton [70] verwendet.
Ausgangspunkt für die Berechnung der Dispersionsrelationen der dipolaren Moden sind die magnetostatischen Maxwellgleichungen ohne Ströme und Ladungen
∇×H = 0
∇·B = 0 ,
(2.38)
mit
B = H + 4πM
.
(2.39)
Diese sind gültig, wenn alle Änderungen quasistatisch, das heißt langsam gegenüber
der Lichtgeschwindigkeit ablaufen. Dieser Fall ist bei allen hier betrachteten Systemen gegeben.
Die Berechnung der Dispersionsrelation erfolgt in zwei Schritten. Zunächst wir
eine allgemeine Differentialgleichung für das skalare Potential des dynamischen Magnetfeldes h(t) hergeleitet (Walker–Gleichung). Diese wird anschließend für das
hier verwendete System eines in–plane magnetisierten Films gelöst.
2.6.1 Walker–Gleichung
Setzt man Heff (t) und M (t) (siehe Gl. (2.19)) in die magnetostatischen Maxwell–
Gleichungen (2.38) ein, erhält man unter Verwendung von Gl. (2.39) für das dyna1 Eine
Herleitung der Dispersionsrelation unter berücksichtigung der kristallographische Aniso-
tropie findet sich in [70].
2.6 Dispersionsrelation dipolarer Moden in in–plane magnetisierten Filmen
15
mische Feld h und die dynamische Magnetisierung m
∇×h = 0
∇ · (h + 4πm) = 0 .
(2.40)
(2.41)
Gleichung (2.40) erlaubt die Definition eines skalaren Potentials Ψ mit
h = −∇Ψ
.
(2.42)
Weiter gilt
m = χ̂h
,
(2.43)
wobei χ̂ der Polder–Suszeptibilitäts–Tensor ist (vgl. Gl. (2.24)). Einsetzen von
Gl. (2.42) und (2.43) in die Maxwellgleichung (2.41) ergibt
∇ · [(1 + 4πχ̂) · ∇Ψ ] = 0
.
Auflösen dieses Ausdrucks liefert die sogenannte Walker–Gleichung
2
∂ Ψ ∂ 2Ψ
∂ 2Ψ
+
+
=0 ,
(1 + χ )
∂ x2
∂ y2
∂ z2
mit
χ=
ωH ωM
ωH2 − ω 2
,
(2.44)
(2.45)
(2.46)
die das Potential Ψ erfüllen muss [73].
Für χ 6= −1 liefert die Walker–Gleichung (2.45) Lösungen, die propagierende
Spinwellen beschreiben. Diese Lösungen werden in den folgenden Kapiteln behandelt.
Ist χ = −1 wird die Walker–Gleichung (2.45) durch ein beliebiges von z unabhängiges Potential Ψ (x, y) gelöst. Man erhält
ω 2 = ωH (ωH + ωM ) .
(2.47)
Dieser Ausdruck entspricht der sogenannten Herring–Kittel–Formel für dünne Filme [74, 75] und beschreibt die ferromagnetische Resonanzabsorption, das heißt eine
homogene Anregung des gesamten Spinsystems. Eine quantenmechanische Herleitung von Gl. (2.47) findet man in [76].
2.6.2 Allgemeine Dispersionsrelation dipolarer Spinwellen
Ausgehend von der Walker–Gleichung (2.45) soll im Folgenden die allgemeine Dispersionsrelation dipolarer Spinwellen in in–plane magnetisierten Filmen der Dicke
16
Grundlagen der Spindynamik
H0
y
ky
− d2
k
φ
kz
0
d
2
mx ex + my ey
x
z
MS ez
Abbildung 2.2: Geometrie zur Berechnung der allgemeinen Dispersionsrelation für dipolare
Spinwellen. Das statische Feld und die statische Magnetisierung sind entlang der z–Achse
orientiert. Der Wellenvektor liegt in der y–z–Ebene unter dem Winkel φ zur Magnetisierungsrichtung.
d in der y–z–Ebene berechnet werden. Wie bereits erwähnt tritt in diesem Fall kein
statisches Streufeld auf; das statische Feld im Inneren des Films entspricht dem angelegten Feld H0 = H0 ez , und für die statische Magnetisierung ergibt sich M0 = MS ez .
Abbildung 2.2 zeigt die verwendete Geometrie. Als Ansatz für das Potential Ψ wird
eine ebene Welle mit (in–plane) Wellenvektor k = (0, k sin(φ ), k cos(φ )) gewählt
Ψi,a = Xi,a(x)eiyk sin(φ ) eizk cos(φ )
.
(2.48)
Dabei ist k = |k| der Betrag des Wellenvektors und φ der Winkel zwischen Wellenvektor und statischer Magnetisierung. Die Indizes i und a kennzeichnen hier und
im Folgenden die Funktion innerhalb (i) und außerhalb (a) des Films. Innerhalb des
Films muss das Potential Ψi die Walker Gleichung (2.45) erfüllen. Außerhalb existiert keine Magnetisierung, das heißt, es gilt die Laplace Gleichung ∆Ψa = 0. Weiter
müssen an den Grenzflächen des Films die Tangentialkomponenten von h und die
Normalkomponente von b = h + 4πm stetig sein
hy,z,i (x = ±d/2) = hy,z,a (x = ±d/2)
bx,i (x = ±d/2) = bx,a (x = ±d/2) .
(2.49)
2.6 Dispersionsrelation dipolarer Moden in in–plane magnetisierten Filmen
17
Daraus folgt für das Potential unter Verwendung von Gl. (2.43) mit dem Polder–
Suszeptibilitäts–Tensor (2.24)
Ψi |x=±d/2 = Ψa |x=±d/2
(2.50)
∂Ψi
∂Ψa ∂Ψi (1 + χ )
− iκ
=
∂x
∂ y x=±d/2
∂ x x=±d/2
(2.51)
Den von x abhängenden Teil Xi,a(x) des Potentials erhält man durch Lösen der
Walker– und Laplace–Gleichung für Ψi,a. Innerhalb des Films ergibt sich
Xi (x) = a cos(qx) + b sin(qx)
mit dem out–of–plane Wellenvektor
s
q=k
1 + χ sin2 (φ )
−
1+χ
Außerhalb des Films kann Xa (x) durch
(
cekx
Xa (x) =
de−kx
(2.52)
.
(2.53)
x ≤ − d2
x ≥ d2
,
,
(2.54)
beschrieben werden. Dabei wurde nur das jeweils physikalisch sinnvolle Vorzeichen
des Exponenten berücksichtigt, da
lim Ψ = 0
(2.55)
x→±∞
gelten muss.
Die Konstanten a, b, c und d müssen über die Randbedingungen (2.50) und
(2.51) bestimmt werden. Aus Gl. (2.50) folgt
d
a cos (−qd/2) + b sin (−qd/2)= ce−k 2
d
a cos (qd/2) + b sin (qd/2) = de−k 2
.
(2.56)
Durch Addition beziehungsweise Subtraktion dieser Gleichungen erhält man Ausdrücke für a und b
d
a=
c + d e−k 2
2 cos q d2
(2.57)
d
c − d e−k 2
b=−
2 sin q d2
.
(2.58)
18
Grundlagen der Spindynamik
Aus der zweiten Randbedingung Gl. (2.51) erhält man
(1 + χ ) [−aq sin (−qd/2) + bq cos (−qd/2)]
d
+ κ k sin(φ ) [a cos (−qd/2) + b sin (−qd/2)] = cke−k 2 (2.59)
und
(1 + χ ) [−aq sin (qd/2) + bq cos (qd/2)]
d
+ κ k sin(φ ) [a cos (qd/2) + b sin (qd/2)] = −dke−k 2
. (2.60)
Addition beziehungsweise Subtraktion dieser Gleichungen und Einsetzen der Ausdrücke für a und b (Gl. (2.59) und (2.60)) liefert
c−d
(1 + χ )q tan(qd/2) − k
κ k sin(φ )
=−
=
c+d
κ k sin(φ )
(1 + χ )q cot(qd/2) + k
.
(2.61)
k2 − (1 + χ )2 q2 − κ 2 k2 sin2 (φ ) + 2(1 + χ )qk cot(qd) = 0
(2.62)
Aus der zweiten Gleichheit ergibt sich2
und — nach Ersetzen von q durch Gl. (2.53) — damit die allgemeine Dispersionsrelation für dipolare Spinwellen in in–plane magnetisierten Filmen
1 + χ sin2 (φ )
1 − (1 + χ ) −
− κ 2 sin2 (φ )
1+χ
 s

s
2
2
1 + χ sin (φ )
1 + χ sin (φ ) 
+ 2(1 + χ ) −
cot kd −
= 0 . (2.63)
1+χ
1+χ
2
Für die weitere Betrachtung muss unterschieden werden, ob der out–of–plane Wellenvektor q reell oder imaginär ist. Im ersten Fall hat das Potential über die Filmdicke eine harmonische Verteilung, und die Spinwellen–Mode ist im gesamten Volumen lokalisiert. Man spricht von Volumenmoden, genauer von Backward–Volume–
Moden (Backward Volume Magnetostatic Spin Waves, BVMSW)3 , da, wie später
gezeigt werden wird, die Dispersion monoton fallend ist und somit Gruppengeschwindigkeit und Wellenvektor in entgegengesetzte Richtungen zeigen. Ist q imaginär, klingt Xi (x) (Gl. (2.52)) exponentiell nach innen ab, das heißt, die Spinwelle
2 Unter
Verwendung von cot(α ) − tan(α ) = 2 cot(2α ), siehe Gl. (2.116) und (2.119) in [77].
im weiteren Verlauf dieser Arbeit werden die englischen Begriffe “Backward–Volume”
3 Hier und
beziehungsweise “Surface” beibehalten, da es sich dabei um feststehende Namen der entsprechenden
Spinwellenmoden handelt.
2.6 Dispersionsrelation dipolarer Moden in in–plane magnetisierten Filmen
19
8
MSSW
ν = ω /2π [GHz]
7,5
7
BVMSW
6,5
6
5,5
0
0
2000
2000
4000
ky [cm−1 ]
4000
6000
6000
8000
8000
10000
10000
kz [cm−1 ]
Abbildung 2.3: Dispersion für dipolare Spinwellen in YIG [79]. (H0 = 1850 Oe, d = 5 µm,
4πMS = 1750 G)
ist an der Oberfläche lokalisiert; man spricht von Surface–Moden (Magnetostatic
Surface Spin Waves MSSW) [78].
Anhand des Ausdrucks für q (Gl. (2.53)) kann der Frequenzbereich bestimmt
werden, in dem q reell ist und damit Backward–Volume–Moden existieren.4 Man
erhält
q
p
ωH (ωH + ωM sin2 (φ )) < ω < ωH (ωH + ωM )
(2.64)
mit
ωM = |γ |4πMS
ωH = |γ |H0
.
(2.65)
Um den Frequenzbereich der Surface–Moden bestimmen zu können, muss zusätzlich geprüft werden, für welche ω (außerhalb des Backward–Volume–Bands)
die Dispersionsrelation (2.63) gelöst werden kann. Wie in [70] gezeigt wird, ist dies
nur in einem Frequenzbereich oberhalb des Backward–Volume–Bands möglich, das
4 Da
cot(qd) eine periodische Funktion ist, erhält man aus Gl. (2.63) unendlich viele Backward–
Volume–Moden, die (solange die Austauschwechselwirkung nicht berücksichtigt wird) alle im selben
Frequenzbereich liegen. Bei denen im Rahmen dieser Arbeit vorgestellten Ergebnissen spielen diese
höheren Moden allerdings keine Rolle, so dass auf eine Behandlung im Folgenden verzichtet wird.
20
Grundlagen der Spindynamik
y
z
y
hs
z
x
λ
x
M (t)
M (t)
λ
(a) Surface–Wellen mit k ⊥ H0
hs
(b) Backward–Volume–Wellen mit k k H0
Abbildung 2.4: Dynamisches Streufeld von dipolaren Spinwellen. Die Pfeile in den Kreisen
verdeutlichen die Richtung der dynamischen Magnetisierung m.
heißt, Surface–Moden existieren nur, wenn
s
p
(ωM sin2 (φ ) − ωH cos2 (φ ))2
ωH (ωH + ωM ) < ω < ωH (ωH + ωM ) +
4 sin2 (φ )
(2.66)
gilt.5 Diese Grenzen zeigen auch, dass es einen minimalen Winkel φc gibt, unterhalb
dessen Surface–Wellen nicht existieren können. Bei diesem Winkel fallen die obere
und die untere Grenzfrequenz zusammen. Für diesen Winkel gilt
r
ωH
φc = arctan
.
(2.67)
ωM
Eine genauere Untersuchung der Spinwellenlokalisierung bei Surface–Wellen
zeigt, dass sich das Maximum der dynamischen Magnetisierung von einer Oberfläche zur anderen verschiebt, wenn die Propagationsrichtung der Welle umgedreht
wird [58]. Surface–Wellen sind demzufolge nicht–reziprok.
Abbildung 2.3 zeigt den Verlauf der Dispersion für beide Moden bei typischen
Parametern.
2.6.3 Einfluss des dynamischen Streufelds auf die Richtung der
Gruppengeschwindigkeit
Wie bereits erwähnt, bildet die statische Magnetisierung eines in–plane magnetisierten Films kein Streufeld aus. Existieren in diesem Film allerdings Spinwellen und
5 Da
bei Surface–Wellen in Gl. (2.62) der cot aufgrund des imaginären Arguments durch den
coth ersetzt wird (coth(x) = i coth(ix)) und dieser nicht periodisch ist, gibt es für Surface–Wellen im
Gegensatz zu den Backward–Volume–Wellen nur eine Mode.
2.6 Dispersionsrelation dipolarer Moden in in–plane magnetisierten Filmen
21
damit eine dynamische Magnetisierung m(t), tritt ein dynamisches Streufeld hs auf.
Dieses wird von der out–of–plane Komponente mx der dynamischen Magnetisierung
erzeugt. Abbildung 2.4 veranschaulicht diesen Effekt für die Spezialfälle k k H0 und
k ⊥ H0 .
Die Energie zum Aufbau dieses Streufeldes wird reduziert, wenn die Wellenlänge abnimmt, da dann die antiparallelen mx –Komponenten enger zusammen liegen.
Für eine vollständige Energiebilanz in Abhängigkeit von der Wellenlänge muss
allerdings auch die in–plane Komponente my der dynamischen Magnetisierung berücksichtigt werden. Bei Surface–Wellen senkrecht zum Feld (vgl. Abb. 2.4(a))
liegt diese Komponente parallel zum Wellenvektor. Daher führt eine Reduzierung
der Wellenlänge zu einer Verringerung des Abstands zwischen antiparallelen my –
Komponenten. Die daraus resultierende Erhöhung der Dipolenergie ist größer als
die Energieabsenkung durch die Reduzierung des Streufeldes, daher steigt die Gesamtenergie mit kleinerer Wellenlänge (das heißt größerem Wellenvektor). Gemäß
E = h̄ω erhöht sich somit die Frequenz der Spinwelle mit größer werdendem Wellenvektor; die Dispersion für Surface–Wellen senkrecht zum Feld ist monoton steigend.
Bei Backward–Volume–Wellen parallel zum Feld (vgl. Abb. 2.4(b)) ist my senkrecht zu k, das heißt benachbarte my –Komponenten zeigen immer in dieselbe Richtung. Die Energieabsenkung durch die Reduzierung des Streufelds wird daher nicht
kompensiert, und die Gesamtenergie der Welle sinkt mit kleinerer Wellenlänge (größerem Wellenvektor). Die Dispersion ist monoton fallend.
Liegt der Wellenvektor unter einen beliebigen Winkel φ zum anliegenden Feld,
kommt es zu einer Vermischung der beschriebenen Situationen, und eine Begründung des Backward– beziehungsweise Forward–Charakters der beiden Spinwellen
Moden über die Energiebilanz ist nur noch eingeschränkt möglich. Die Dispersionsrelation (2.63) zeigt allerdings, dass dieser Charakter für beliebige Winkel φ erhalten
bleibt [70].
2.6.4 Spezialfälle der Dispersionsrelation
Untersucht man die Spinwellenpropagation in Wellenleitern, werden üblicherweise
die Fälle k k H0 oder k ⊥ H0 realisiert. Im Folgenden sollen daher aus der allgemeinen Dispersionsrelation diese beiden Spezialfälle abgeleitet werden.
Backward–Volume–Wellen mit k k H0
Für den Fall k k H0 , das heißt φ = 0 erhält man aus Gl. (2.53)
s
1
q=k
−
.
1+χ
(2.68)
22
Grundlagen der Spindynamik
Damit q reell ist, muss also 1 + χ < 0 gelten. Damit lässt sich die Gl. (2.63) zu
!
p
kd
=0
(2.69)
1 + (1 + χ ) − 2 −(1 + χ ) cot p
−(1 + χ )
vereinfachen, woraus sich für die Dispersion für Backward–Volume–Wellen parallel
zum Feld6
p
2p
k=
−(1 + χ ) arctan
−(1 + χ )
(2.70)
d
ergibt.
Surface–Wellen mit k ⊥ H0
Wie bereits erwähnt ist q bei Surface–Wellen imaginär. Für den hier betrachteten
Spezialfall k ⊥ H0 , das heißt φ = π/2 gilt q = ik, und die Dispersion (2.63) vereinfacht sich zu
1 + (1 + χ )2 − κ 2 + 2(1 + χ ) coth(kd) = 0 .
(2.71)
Auflösen dieses Ausdrucks nach ω liefert die Dispersion für Surface–Wellen senkrecht zum Feld
ω2 ω 2 = ωH (ωH + ωM ) + M 1 − e−2kd
.
(2.72)
4
Abhängigkeit der Dispersion vom angelegtem Feld und der Magnetisierung
Betrachtet man die Grenzfrequenzen für Backward–Volume–Wellen (2.64) und Surface–Wellen (2.66), so fällt auf, dass diese Grenzen Funktionen des angelegten Felds
H0 und der Magnetisierung MS sind. Änderungen dieser Parameter führen also zu
einer Verschiebung (beziehungsweise Stauchung und Streckung) der Dispersionskurve entlang der Frequenzachse und damit, bei beibehaltener Frequenz, zu einer
Änderung des Wellenvektors. Abbildung 2.5 zeigt dieses Verhalten für die in diesem
Kapitel behandelten Spezialfälle.
2.6.5 Wellenvektorabhängigkeit der Propagationsrichtung
Bei der bisherigen Betrachtung wurde die Ausbreitung der Spinwelle ausschließlich
über den Wellenvektor charakterisiert. Im Experiment direkt beobachtbar ist allerdings nur die Propagationsrichtung der Welle, das heißt die Gruppengeschwindigkeit
vg = ∇k ω
6 Unter
Verwendung von arctan
2α
1−α 2
.
= 2 arctan(α ), siehe Gl. (2.157a) in [77].
(2.73)
2.6 Dispersionsrelation dipolarer Moden in in–plane magnetisierten Filmen
Frequenz [GHz]
7,5
7,0
H0 = 1850 Oe
4πMS = 1750 G
6,5
H0 = 1750 Oe
4πMS = 1750 G
6,0
H0 = 1850 Oe
4πMS = 1650 G
5,5
5,0
0
5000
10000
15000
20000
25000
Wellenvektor [cm−1 ]
Abbildung 2.5: Änderung der Dispersion bei Änderung des angelegten Felds H0 und der
Magnetisierung MS . Die Dicke des betrachteten Films ist in allen Fällen d = 5 µm.
In anisotropen Medien ist die Gruppengeschwindigkeit im Allgemeinen nicht parallel zum Wellenvektor. Im Folgenden soll nun die Abhängigkeit der Richtung der
Gruppengeschwindigkeit von der Richtung des Wellenvektors bestimmt werden.
Die Anisotropie in dem im Rahmen dieser Arbeit betrachteten System wird durch
das in der Filmebene angelegte Feld induziert. Es ist daher sinnvoll, alle Richtungen
in Bezug zum Feld (hier entlang der z–Achse) anzugeben. Neben dem bereits eingeführten Winkel φ (Richtung des Wellenvektors in Bezug auf das angelegte Feld,
siehe Abb. 2.2) wird im Folgenden auch die Richtung der Gruppengeschwindigkeit
(das heißt die Propagationsrichtung)
vg,y
θ = arctan
(2.74)
vg,z
betrachtet.
Bei der Berechnung von θ tritt das Problem auf, dass die Dispersion nicht in einer
expliziten Form sondern als implizite Funktion f(ω , k, φ ) = 0 (Gl. (2.63)) vorliegt.
Die Berechnung von vg,y und vg,z muss daher gemäß
∂f
∂f
∂f
∂f
vg,y =
vg,z =
(2.75)
∂ ky ∂ ω
∂ kz ∂ ω
erfolgen.
23
24
Grundlagen der Spindynamik
40
H0 = 1820 Oe
H0 = 1830 Oe
H0 = 1840 Oe
H0 = 1860 Oe
H0 = 1880 Oe
30
20
θ [◦ ]
10
0
-10
-20
-30
-40
-80
-60
-40
-20
0
20
40
60
80
φ [◦ ]
Abbildung 2.6: Abhängigkeit der Propagationsrichtung θ von der Richtung des Wellenvektors φ für verschiedene Felder (ω = 2π · 7,132 GHz, d = 5 µm, 4πMS = 1750 G).
Die nötigen partiellen Ableitungen können aus Gl. (2.63) analytisch berechnet
werden. Die Durchführung dieser Rechnung ist allerdings sehr langwierig, da nahezu alle Größen in Gl. (2.63) Funktionen von ω , ky und kz sind. Hier wird daher auf
die Darstellung der einzelnen Teilschritte verzichtet und nur die berechneten θ (φ )–
Kurven wiedergegeben.
Stellt man die Richtung der aus Gl. (2.75) berechneten Gruppengeschwindigkeiten (θ ) als Funktion von φ dar, ergeben sich (für Backward–Volume–Wellen) die
in Abb. 2.6 gezeigten Kurven. Es fällt auf, dass für Wellenvektoren für die φ zwischen 20◦ und 40◦ beziehungsweise 60◦ und 70◦ liegt, die Propagationsrichtung θ ,
insbesondere für kleine Felder, nur schwach von φ abhängt. Dieser Effekt wurde im
Rahmen dieser Arbeit genutzt, um stabile, lateral begrenzte Spinwellen (sogenannte
Kaustikstrahlen) zu erzeugen.
Kapitel 3
Brillouin–Lichtstreuspektroskopie an
mikrowellenangeregten
Spinwellenpaketen
Im Folgenden werden die experimentellen Techniken für die im Rahmen dieser
Arbeit durchgeführten Untersuchungen vorgestellt. Zunächst wird dabei kurz auf
die Anregung von Spinwellen mit Mikrowellen und die dazu notwendigen Schaltungen eingegangen (Kapitel 3.1). Im Anschluss wird der typische Probenaufbau
vorgestellt (Kapitel 3.2). Den Schwerpunkt dieses Kapitels bildet die Besprechung
der Brillouin–Lichtstreuspektroskopie (Kapitel 3.3) und deren Erweiterungen zur
orts- und zeitaufgelösten BLS (Kapite 3.4) sowie zur phasenaufgelösten BLS (Kapitel 3.5). Einen allgemeinen Überblick über die Brillouin–Lichtstreuspektroskopie
und andere optische Untersuchungsmethoden liefert zum Beispiel [80].
3.1 Anregung und Detektion von Spinwellen durch
Mikrowellenmesstechnik
Die hier untersuchten Spinwellen wurden mit Hilfe von Mikrowellensignalen erzeugt. Dabei koppelt das magnetische Wechselfeld einer Mikrowellenantenne an die
magnetischen Momente der Probe und regt diese zur Präzession an [81]. Findet diese Anregung lokal begrenzt statt, kann sich die Störung in der Probe ausbreiten, und
es bildet sich eine propagierende Spinwelle aus. Die Frequenz sowie die Amplitude
dieser Spinwelle wird dabei durch Frequenz und Amplitude des anliegenden Mikro-
26
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
Referenzsignal
zur
Probe
Mikrowellenquelle
Leistungs- Ferritisolator
teiler
schneller Verstärker
Schalter
Abschwächer
Synchronisation
Pulsgenerator
(a) Eingangsnetzwerk
von der
Probe
Detektor
Oszilloskop
Verstärker
Abschwächer
(b) Ausgangsnetzwerk
Abbildung 3.1: Schaltplan des Eingangs- (a) und Ausgangsnetzwerks (b) des Mikrowellenaufbaus.
wellensignals bestimmt. Zur Detektion dieser Welle kann der umgekehrte Prozess
verwendet werden. Die Spinwelle (genauer: das von der Spinwelle erzeugte Streufeld b(t) = h(t) +4πm(t)) induziert in einer Mikrowellenantenne eine hochfrequente
Wechselspannung, die anschließend nachgewiesen werden kann. Im Folgenden werden die dazu verwendeten Schaltungen kurz vorgestellt. Ein genereller Überblick
über die verwendete Mikrowellentechnik findet sich zum Beispiel in [82, 83].
Abbildung 3.1(a) zeigt den Schaltplan des Eingangsnetzwerks. Die verwendete Mikrowellenquelle liefert ein kontinuierliches Ausgangssignal einstellbarer Leistung und Frequenz. Ein Leistungsteiler stellt ein Referenzsignal zur Verfügung,
das zum Betrieb der phasenaufgelösten Brillouin–Lichtstreuspektroskopie benötigt
wird (vgl. Kapitel 3.5). Ein schneller Mikrowellenschalter wandelt anschließend
das cw–Signal der Quelle in Pulse einstellbarer Länge um. Der Pulsgenerator, der
diesen Schalter ansteuert, wird auch zur Synchronisation des Oszilloskops im Ausgangsnetzwerk und der Zeitauflösung des optischen Aufbaus verwendet (vgl. Kapitel 3.4). Die Pulse werden anschließend verstärkt und passieren einen einstellbaren
Abschwächer. Dieser erlaubt eine feine Kontrolle der Mikrowellenintensität und damit der Intensität der angeregten Spinwelle. Dazu ist anzumerken, dass die Intensität
der Spinwelle nicht nur von der anliegenden Mikrowellenleistung sondern auch von
der Anregungseffizienz der Antenne und damit von der Wellenlänge der Spinwellen
abhängt (da langwellige Spinwellen effizienter angeregt werden als kurzwellige).
Eine Änderung des angelegten magnetischen Felds führt daher auch zu einer Änderung der Intensität der Spinwelle, so dass bei Messreihen darauf zu achten ist, die
3.2 Aufbau der Probe
27
Intensität der Mikrowellenpulse entsprechend zu ändern, um vergleichbare Resultate zu erhalten. Die beiden Isolatoren im Eingangsnetzwerk schützen die Quelle
und den Verstärker von den am (geöffneten) Schalter beziehungsweise der Antenne
reflektierten Mikrowellen.
Das Ausgangsnetzwerk ist in Abb. 3.1(b) dargestellt. Die von der Probe kommenden Mikrowellen sind zu schwach, um direkt erfasst zu werden. Sie müssen
daher verstärkt werden. Ein einstellbarer Abschwächer erlaubt eine Anpassung der
Intensität. Der Abschwächer ist dabei vor den Verstärker geschaltet, da dieser nur
bis zu einer bestimmten Eingangsleistung linear arbeitet und daher das Signal, das
von der Probe kommt, gegebenenfalls reduziert werden muss. Der Mikrowellendetektor wandelt das Mikrowellensignal in eine Spannung proportional zu deren Intensität um. Diese kann auf einem Oszilloskop dargestellt werden. Dabei muss beachtet werden, dass die Beziehung zwischen nachgewiesener Mikrowellenleistung
und Ausgangsspannung häufig nichtlinear ist. Das gemessene Signal muss daher
umgerechnet werden, um eine qualitative Aussage zu ermöglichen.
3.2 Aufbau der Probe
Die hier untersuchten Spinwellen wurden in dünnen Filmen (ca. 5 – 7 µm dick) aus
Yttrium–Eisen–Granat Y3 Fe5 O12 (Yttrium–Iron–Garnet, YIG, siehe auch [84]) angeregt. Diese wurden durch Flüssigphasenepitaxie auf ein Substrat aus Gallium–
Gadolinium–Granat (GGG) gewachsen.1 Beide Materialien sind transparent und
können daher mit Hilfe der Brillouin–Lichtstreuspektroskopie (siehe Kapitel 3.3 –
3.5) untersucht werden.
Sättigungsmagnetisierung 4π MS
1750 G
gyromagnetisches Verhältnis γ
2π · 2,8 · 106 rad/s
Oe
FMR–Linienbreite 2∆ H
Gilbert–Dämpfungsparameter α
0,3 – 0,6 Oe
5,6 · 10−4
Tabelle 3.1: Eigenschaften der verwendeten YIG–Filme.
In Tabelle 3.1 sind die typischen Eigenschaften der verwendeten YIG–Filme zusammengefasst. Für die hier durchgeführten Untersuchungen ist dabei insbesondere
die geringe Dämpfung (das heißt der kleine Wert des Gilbert–Dämpfungsparameters
1 Die
im Rahmen dieser Arbeit verwendeten Proben wurden von Scientific Research Company
“Carat”, R&D Institute of Materials, Division of Crystal Growth and Technology, Lviv, Ukraine
hergestellt.
28
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
Zuleitungen der
Mikrowellensignale
Mikrowellenantennen
Mikrowellenantennen
YIG Wellenleiter
(a) YIG Spinwellenwellenleiter
Eingangswelleleiter
Propagationsfläche
(b) YIG Wellenleiterantenne
Abbildung 3.2: Beispiele der verwendeten Proben. (a) YIG Spinwellenwellenleiter. Anregung und Nachweis der Spinwellen erfolgt durch die Mikrowellenantennen. (b) YIG Wellenleiteantenne. Der Übergang vom Eingangswellenleiter zur Propagationsfläche dient als
Antenne, die unbegrenzte Spinwellen in einem weiten Winkelbereich anregt.
α , siehe Gl. (2.17)) von Bedeutung, da dadurch eine Beobachtung der Spinwellen über makroskopische Distanzen (ca. 1 cm) möglich ist. Zur Beschreibung der
experimentellen Resultate in den Kapiteln 4 – 6 wird üblicherweise nicht der hier
genannte Literaturwert der Sättigungsmagnetisierung 4πMS verwendet, sondern eine effektive Magnetisierung durch einen Fit der entsprechenden Dispersionsrelation
an die gemessenen Frequenz–Wellenvektor–Paaren bestimmt. Diese berücksichtigt
Änderungen von MS durch Temperatur oder Oberflächendefekte (durch die nasschemische Strukturierung) sowie ein abhängig von der Richtung von k in Bezug auf
die kristallographischen Achsen eventuell vorhandenes (geringes) Anisotropiefeld.
Derselbe Fit erlaubt auch die Bestimmung der Filmdicke d.
Die zu untersuchende Probe wird auf ein Substrat aus Duroid® befestigt. Mikrostreifen–Antennen auf diesem Substrat dienen zur Anregung und zum Nachweis
der Spinwellen; ein Fenster zwischen den Antennen erlaubt die Untersuchung der
Spinwellen mit optischen Methoden.
Abbildung 3.2 zeigt Beispiele für die hier verwendeten Probenaufbauten. In
Abb. 3.2(a) ist ein typischer Spinwellenwellenleiter dargestellt, wie er zum Beispiel
bei der Untersuchung von Solitonen (siehe zum Beispiel [32–35]) oder einigen der
hier präsentierten Resultate verwendet wurde.
Im Rahmen dieser Arbeit wurde erstmals eine sogenannte Wellenleiterantenne
3.2 Aufbau der Probe
29
-10
p
ωH (ωH + ωM )
Transmission [dB]
-20
H0 = 1800 Oe
-30
-40
-50
-60
H0 = 1840 Oe
6,9
7,0
7,1
7,2
7,3
ν = ω /2π [GHz]
Abbildung 3.3: Transmissionscharakteristik eines Spinwellenwellenleiters aus YIG (Filmdicke d = 6 µm) für Backward–Volume–Wellen mit H0 = 1800 Oe und H0 = 1840 Oe.
verwendet, die in Abb. 3.2(b) dargestellt ist.2 Spinwellen werden zunächst im Eingangswellenleiter angeregt und propagieren dort. Der Übergang zur Propagationsfläche wirkt wie eine (schmale) Antenne, die unbegrenzte Spinwellen in einem weiten (Wellenvektor–)Winkelbereich anregt.
Abbildung 3.3 zeigt eine typisches Beispiel einer Transmissionscharakteristik eines Spinwellenwellenleiters aus YIG. Dargestellt ist die Transmission des Wellenleiters in Abhängigkeit der Frequenz, das heißt der Anteil der Mikrowellenleistung an
der Eingangsantenne, der an der Ausgangsantenne noch nachgewiesen werden kann.
Die Spinwellen propagieren parallel zum angelegten Feld. Wie bereits theoretisch
gezeigt (siehe Kapitel 2.6.4), verschiebt sich das Transmissionsband bei Erhöhung
des magnetischen Felds zu größeren Frequenzen.
Die obere Grenzfrequenz für
p
Backward–Volume–Wellen parallel zum Feld ωH (ωH + ωM ) (vgl. Gl. (2.64)) ist
deutlich bei etwa 7,1 GHz beziehungsweise 7,22 GHz zu erkennen. Für kleinere
Frequenzen, das heißt in dieser Geometrie kleinere Wellenlängen der angeregten
Spinwellen (vgl. Kapitel 2.6.4), nimmt die Transmission ab. Ursache hierfür ist zum
2 Die
Herstellung dieser Probe erfolgte durch nasschemische Strukturierung eines YIG–Wavers
und wurde von Christian Sandweg, Andrii Chumak und Sandra Wolff im Nano+Bio Center der TU
Kaiserslautern durchgeführt.
30
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
einen, dass die Effektivität der Spinwellenanregung durch Mikrowellen für kurzwellige Spinwellen abnimmt, da dann die Breite der Antenne vergleichbar mit der
Wellenlänge der Spinwellen wird. Außerdem nimmt die Gruppengeschwindigkeit
mit kleiner werdender Frequenz leicht ab, das heißt die räumliche Dämpfung nimmt
geringfügig zu, da
−α vzg
I ∼ e−α t = e
(3.1)
gilt.
3.3 Brillouin–Lichtstreuspektroskopie
Der Nachweis von Spinwellen durch eine Mikrowellenantenne hat den Nachteil,
dass die Wellen nur an einer Position und dort auch nur integral über die gesamte Länge der Antenne registriert werden können. Im Gegensatz dazu erlaubt die
Brillouin–Lichtstreuspektroskopie (BLS) den Nachweis von Spinwellen [22] (und
Phononen [85]) in einem beliebigen Punkt; die erreichbare Auflösung wird dabei nur
durch die Fokusgröße des Lasers begrenzt. Sie ist damit — insbesondere mit den in
diesem Kapitel vorgestellten Erweiterungen zur orts-, zeit- und phasenaufgelösten
BLS — vielseitig zur Untersuchung verschiedenster Fragestellungen im Bereich der
Spindynamik einsetzbar (siehe zum Beispiel [3, 4, 24, 43, 86–90]).
3.3.1 Brillouin–Lichtstreuprozess
Unter Brillouin–Lichtstreuung versteht man die inelastische Streuung von Licht an
Anregungen des Festkörpers, wie zum Beispiel Phonenen oder Magnonen. Eine einfache Beschreibung dieser Streuung ist im Bild der zweiten Quantisierung (vgl. zum
Beispiel [91]) möglich. Sie lässt sich darin als Wechselwirkung eines einfallenden
Photons mit einem Magnon verstehen (vgl. Abb. 3.4).
Wird bei der Streuung ein Magnon der Frequenz ω vernichtet, muss sich aufgrund der Energieerhaltung die Frequenz des Photons ωL erhöhen. Wird ein Magnon erzeugt, wird die Frequenz des Photons vermindert. Man erhält daher für die
Frequenz des gestreuten Photons
ωL′ = ωL ± ω
,
(3.2)
wie man durch Multiplikation von Gl. (3.2) mit h̄ sieht. Gleichzeitig ändert sich
aufgrund der Impulserhaltumg der Wellenvektor des gestreuten des Photons
kL′ = kL ± k
,
(3.3)
3.3 Brillouin–Lichtstreuspektroskopie
31
ωL
Gestreutes Photon
ωL ± ω , kL ± k
Stokes
Anti–Stokes
ωL − ω
ωL + ω
Spinwelle
ω, k
Spektrum des gestreuten Lichts
Einfallendes Photon
ωL , kL
(a) Prinzip
(b) Spektrum
Abbildung 3.4: (a) Prinzip der Brillouin–Lichtstreuung. Ein Photon wird unter Erzeugung
oder Vernichtung eines Magnons gestreut. Dadurch verschiebt sich die Frequenz des eingestrahlten Photons um die Magnonenfrequenz. (b) Schematische Darstellung des Spektrum
des gestreuten Lichts.
wie ebenfalls durch Multiplikation mit h̄ gezeigt werden kann. Gleichung (3.3) erlaubt damit bei Kenntnis der Wellenvektoren (das heißt von Wellenlänge und Winkel) des einfallenden und gestreuten Lichts, die Bestimmung des (in–plane) Wellenvektors der untersuchten Spinwelle (siehe zum Beispiel [A11, 24]).
Wird bei der Streuung ein Magnon erzeugt, spricht man von einem Stokes–
Prozess, wird ein Magnon vernichtet von einem Anti–Stokes–Prozess. Bei Zimmertemperatur sind beide in vielen Fällen nahezu gleich wahrscheinlich. Eine wichtige
Ausnahme ist die Streuung an Oberflächenmoden (vgl. Kapitel 2.6). Aufgrund des
definierten Umlaufsinnes dieser Moden finden Stokes– und Anti–Stokes–Prozesse
mit unterschiedlicher Wahrscheinlichkeit statt [92].
Weiter ist zu beachten, dass bei der Streuung die Polarisationsebene des inelastisch gestreuten Lichts um π/2 gedreht wird [93]. Da diese Drehung bei der Streuung an Phononen oder bei elastisch gestreutem Licht nicht auftritt, kann ein Polarisationsfilter, der senkrecht zur ursprünglichen Polarisationsrichtung steht, verwendet
werden, um diese Komponenten des gestreuten Lichts herauszufiltern.
Klassisch kann die Brillouin–Lichtstreuung durch eine Veränderung der Dielektrizitätskonstante ε beschrieben werden: Eine propagierende Spinwelle tritt durch
die Spin–Bahn–Kopplung mit dem Elektronensystem des Festkörpers in Wechselwirkung und führt so zu einer periodischen Fluktuation von ε und damit des Brechungsindex n [93–95]. Diese beeinflusst das einfallende Licht, so dass nach der
Streuung Komponenten mit den Frequenzen ωL ± ω entstanden sind.
32
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
3.3.2 Experimenteller Aufbau
Der Aufbau der hier verwendeten BLS–Anlage ist in Abb. 3.5 gezeigt. Als Lichtquelle wird ein diodengepumpter frequenzverdoppelter Nd:YVO4 Laser mit der Wellenlänge λ = 532 nm verwendet. Ein kleiner Teil des Laserstrahls wird mit einem
Strahlteiler abgeteilt und dient zur Stabilisierung des Interferometers. Der verbleibende Teil wird auf die Probe fokussiert. Der Strahl durchdringt die Probe und wird
inelastisch an den Spinwellen gestreut, man spricht von “Forward–Scattering”.3 Eine zweite Linse sammelt das gestreute Licht.
Ein räumlicher Filter, der aus zwei Linsen und einer Lochblende besteht, unterdrückt das Hintergrundrauschen, das zum Beispiel durch die Raumbeleuchtung
verursacht wird. Ein Shutter–System führt Referenzstrahl und Messstrahl wieder
zusammen. Zur Frequenzselektion wird ein Tandem–Fabry–Pérot–Interferometer
(vgl. Kapitel 3.3.3) verwendet.
Das Licht, das vom Interferometer durchgelassen wird, passiert einen weiteren
räumlichen Filter und wird von einem Photodetektor4 registriert. Die Datenaufnahme erfolgt mit einem Computer.
Die Ansteuerung des Shutter–Systems stellt sicher, dass im Wellenlängenbereich
des Lasers der Referenzstrahl und im Bereich des inelastisch gestreuten Lichts der
Messstrahl verwendet wird. Dadurch ist der Photodetektor vor der hohen Intensität des elastisch gestreuten Lichts geschützt. Außerdem wird sichergestellt, dass
unabhängig von den Transmissionseigenschaften der Probe immer die gleiche Laserintensität zur Stabilisierung des Interferometers zur Verfügung steht.
3.3.3 Das Tandem–Fabry–Pérot–Interferometer
Verwendet man ein einfaches Fabry–Pérot–Interferometer (Etalon) zur Frequenzselektion, ist keine eindeutige Zuordnung zwischen Plattenabstand und durchgelassener Wellenlänge möglich [98]. Haben die beiden Etalon–Spiegel den Abstand d,
wird Licht nur dann transmittiert, wenn die Wellenlänge λ die Bedingung
n
λ
=d
2
(3.4)
erfüllt. Da n eine beliebige natürliche Zahl sein kann, wird diese Bedingung von
vielen Wellenlängen erfüllt. Das von J. R. Sandercock entwickelte Tandem–Fabry–
Pérot–Interferometer löst dieses Problem durch die Verwendung eines zweiten Etalons [99–101].
3 Bei
nicht transparenten Proben kann auch das rückwärts gestreute Licht verwendet werden; man
spricht dann von Backward–Scattering“.
”
4 In dem hier verwendeten Aufbau wird dazu eine Avalanche–Photodiode [97] verwendet.
PC-Steuerung
- Stabilisierung
- Daten-Akkumulation
und -Verarbeitung
- Darstellung
Räumlicher
Filter
Zeitauflösender
Detektor
Prisma
Pulsgenerator
FP2
Mikrowellenverstärker
Probe
Scan-Richtung
Räumlicher
Filter
Magnet
N
Polarisationsanalysator
Mikrowellenquelle
Schneller
Schalter
Retroreflektoren
z
FP1
ShutterSystem
y
S
Magnet
3.3 Brillouin–Lichtstreuspektroskopie
Photodetektor
Scan-Bühne
Tandem-Fabry-PerotInterferometer
Laser
33
Abbildung 3.5: Aufbau der Brillouin–Lichtstreuspektroskopie. Die einzelnen Komponenten werden im Text näher erklärt. Abbildung
nach [96].
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
δ L · cos (θ )
FP2
ω
ω
ω
FP2
ScanRichtung
Umlenkspiegel
θ
FP1
ω
Transmission
34
FP1
TFP
Scan-Bühne
Spiegelabstand
δL
(a) Aufbau
(b) Funktion
Abbildung 3.6: (a) Aufbau des Tandem–Fabry–Pérot–Interferometers. (b) Funktion des
Tandem–Fabry–Pérot–Interferometers. ω ist die Frequenz der streuenden Spinwelle. Abbildung entnommen aus [24].
Das Prinzip ist in Abb. 3.6(a) dargestellt. Die beiden Etalons sind in einem Winkel θ zueinander angebracht und bestehen aus jeweils zwei parallelen, hochreflektierenden Spiegeln. Ein System aus Umlenkspiegeln und Prismen sorgt dafür, dass
beide zur Kontrastverbesserung mehrfach durchlaufen werden (vgl. Abb. 3.5). Jeweils einer der Spiegel jedes Etalons ist auf einer gemeinsamen, beweglichen Bühne
befestigt, so dass die Spiegelabstände simultan geändert werden können. Eine Änderung des Spiegelabstandes von FP1 um δ L führt dabei zu einer Abstandsänderung
um δ L · cos (θ ) in FP2.
Sind beide Etalons in Resonanz, das heißt transmittieren sie Licht der Wellenlänge λ , so führt eine Abstandsänderung von δ L = λ /2 in FP1 zum Erreichen
der nächsten Transmissionsordnung. FP2 ist dann allerdings nicht mehr in Resonanz, so dass das Licht dieses Etalon nicht passieren kann (vgl. Abb. 3.6(b)). Damit
ist sichergestellt, das nur eine Transmissionsordnung hinter den Etalons mit nennenswerter Intensität nachgewiesen werden kann. Die Tandem–Anordnung erlaubt
also eine eindeutige Zuordnung zwischen der Abstandsänderung δ L und der durchgelassenen Wellenlänge und ermöglicht damit eine präzise Bestimmung der Spinwellenfrequenz.
Die Verschiebung der Scan–Bühne erfolgt durch einen Piezokristall. Wird die
anliegende Spannung geändert, ändert sich der Spiegelabstand und damit die durchgelassene Wellenlänge.
Während der gesamten Dauer der Messung (diese kann einige Stunden betragen)
müssen die Spiegel der Etalons exakt parallel bleiben. Diese Stabilisierung wird
mittels weiterer Piezokristalle durch ein Computerprogramm gesteuert, das auch die
3.4 Orts- und zeitaufgelöste Brillouin–Lichtstreuspektroskopie
Antenne
YIG
35
Laser
4. Speicherinhalt wird
um eins erhöht
2. Inelastisch gestreutes
Photon stopt Zähler
1. Triggersignal
startet Spinwelle
und Zähler
Stop
Zähler
Intensität
Start
3. Zählerstand adressiert
Speicher
Zeitprofil der
Spinwelle
Speicherstellen
(Zeit)
Abbildung 3.7: Schematische Darstellung der zeitaufgelösten BLS–Messung.
Datenerfassung übernimmt [102]. Zur weiteren Erhöhung der Stabilität dient eine aktive Vibrationsdämpfung; außerdem ist das Interferometer durch den Einbau
in eine geschlossene Box weitestgehend von Temperaturänderungen und Luftbewegungen isoliert.
3.4 Orts- und zeitaufgelöste Brillouin–Lichtstreuspektroskopie
Zur Bestimmung der räumlichen Verteilung der Spinwellenintensität kann die Probe
mit Schrittmotoren in y– und z–Richtung (das heißt in der Probenebene) bewegt
werden. Die erreichbare Auflösung ist dabei durch den Durchmesser des Laserspots
beschränkt, der bei dem hier verwendeten Aufbau etwa 50 µm beträgt.5 Die Anzahl
der inelastisch gestreuten Photonen ist dann proportional zur Intensität der Spinwelle
am Ort des Lasers.
Die zur Realisierung einer Zeitauflösung notwendigen Komponenten wurden bereits in Abb. 3.5 dargestellt. Derselbe Pulsgenerator, der auch den Mikrowellenschal5 Verwendet
man anstelle einer ‘normalen’ Linsen ein Mikroskop–Objektiv, kann die Auflösung
auf bis zu 250 nm gesteigert werden (siehe zum Beispiel [90, 103]).
36
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
ter ansteuert, startet einen schnellen Zähler mit einer Zeitbasis von 1,2 GHz. Dieser
wird gestoppt, sobald ein inelastisch gestreutes Photon registriert wird. Der aktuelle
Zählerstand dient zur Adressierung einer Speicherzelle in einem Array, deren Inhalt
um Eins erhöht wird. Nach mehrmaliger Wiederholung dieses Prozesses gibt der
Inhalt des Speicherarrays die zeitliche Intensitätsverteilung am Ort des Laserspots
wieder. Die Messmethode wird ausführlicher in [96, 104] beschrieben. Die zeitliche Auflösung wird durch den Mehrfachdurchgang der Etalons bestimmt und beträgt
hier etwa 1,8 ns. Abbildung 3.7 illustriert das beschriebene Verfahren.
Eine Kombination von orts- und zeitaufgelösten Messungen liefert eine dreidimensionale Matrix (zwei Ortskoordinaten, eine Zeitkoordinate). Diese Matrix
enthält die Anzahl der am jeweiligen Ort zur jeweiligen Zeit inelastisch gestreuten Photonen. Mit Hilfe eines Computerprogrammes6 können daraus die (zweidimensionalen) Intensitätsverteilungen der gemessenen Spinwelle zu jedem Zeitpunkt
bestimmt und entweder als einzelne Bilder (wie zum Beispiel in Abb. 3.9(a)) oder
als Film dargestellt werden.
3.5 Phasenaufgelöste Brillouin–Lichtstreuspektroskopie
Der bisher vorgestellte BLS–Aufbau erlaubt nur die Bestimmung der Intensität und
nicht der Phase von Spinwellen, obwohl bei der inelastischen Streuung die Phaseninformation der Spinwelle auf das gestreute Photon übertragen wird. Da zur Detektion
ein Photomultiplier eingesetzt wird, geht diese Information allerdings verloren, und
man erhält nur ein Signal, das proportional zur Spinwellenintensität ist. Die vor einigen Jahren entwickelte phasenaufgelöste BLS [A1, A3] umgeht dieses Problem und
ermöglicht die Untersuchung der Phaseneigenschaften von mikrowellenangeregten
Spinwellen.
Der prinzipielle Aufbau der phasenaufgelösten BLS ist in Abb. 3.8 dargestellt.
Das inelastisch gestreute Licht wird mit einem kohärenten Referenzsignal gleicher
Frequenz überlagert. Zur Erzeugung dieses Referenzsignals wird ein Teil des eingestrahlten Lichts um den Betrag der Spinwellenfrequenz frequenzverschoben. Dazu wird ein elektro–optischer Modulator (EOM) verwendet (siehe Anhang A und
[105]), der mit demselben Mikrowellensignal betrieben wird, das auch die Spinwellen erzeugt. Dies garantiert nicht nur, dass beide Signale dieselbe Frequenz haben
sondern auch die notwendige Phasenkohärenz. Das daraus resultierende Interferenzbild enthält Informationen über Amplitude und Phase der betrachteten Spinwelle.
6 Entwickelt
versität, Kiev.
von Andrii Chumak und Oleksandr Dzyapko, Nationalen Taras Schewtschenko Uni-
3.5 Phasenaufgelöste Brillouin–Lichtstreuspektroskopie
Laser
Signal Kanal
Magnet
N
37
Fabry-PerotInterferometer
Referenz Kanal
Photodetektor
Elektrooptischer
Modulator
S
Magnet
Abbildung 3.8:
Schematischer
Lichtstreuspektroskopie.
Aufbau
der
Phasenaufgelösten
Brillouin–
Mit einem Abschwächer kann die Intensität des Referenzsignals eingestellt werden.
Ein Phasenschieber erlaubt die Festlegung des Phasen–Nullpunkts.
Interferenz zwischen dem gemessenen Signal und einem koheränten Referenzsignal wurde bereits bei Experimenten mit Mikrowellen zur Bestimmung der Phaseneigenschaften eingesetzt und lieferte dort gute Ergebnisse [41]. Während bei
Mikrowellenexperimenten das Referenzsignal und das Messsignal im Allgemeinen
räumlich getrennt sind und erst nach dem Experiment zusammengeführt werden,
liegen bei dem hier verwendeten Aufbau der Strahlengang von Referenz- und Messsignal übereinander. Dies ist notwendig, da die Wellenlänge des verwendeten Lasers
deutlich kürzer ist als die Wellenlänge von Mikrowellen (532 nm gegenüber einigen
Zentimetern). Daher können bereits kleine Änderungen im Strahlengang, zum Beispiel durch thermische Ausdehnung, Vibrationen beim Verschieben der Probe oder
sogar geringfügige Änderungen der Dicke der Probe das Interferenzbild stören.
Weiter ist zu beachten, dass das inelastisch gestreute Licht eine Polarisationsdrehung um 90◦ erfährt, während die Polarisationsrichtung des durch den EOM
frequenzverschobenen Lichts nicht geändert wird. Um trotzdem ein Interferenzsignal zu erhalten, ist es daher notwendig, die Polarisation beider Signale anzupassen.
Dazu wird ein Polarisator (hinter EOM und Probe) verwendet, dessen Polarisationsebene auf einen Wert zwischen 0 und 90◦ eingestellt ist. Da dabei die Intensität
beider Signale reduziert wird und sich die Intensität des Referenzsignals einfacher
erhöhen lässt, ist es im Allgemeinen günstiger, einen Winkel näher an 90◦ zu wählen.
Im Rahmen dieser Arbeit wurden üblicherweise ein Wert von 70◦ verwendet. Wie
38
Brillouin–Lichtstreuspektroskopie an mikrowellenangeregten Spinwellenpaketen
138,9 ns
λ/2
max
(a) Ortsaufgelöste Messung
72,9 ns
λ
min
(b) Phasenaufgelöste Messung
Abbildung 3.9: Tunneln von Spinwellen als Beispiel einer orts-, und phasenaufgelösten BLS–
Messung. (a) Ortsaufgelöste Messung. Ein Teil der Welle tunnelt durch die Lücke, während
der Rest reflektiert wird und vor der Lücke eine stehende Welle ausbildet. (b) Phasenaufgelöste Messung vor der Reflektion.
kürzlich vorgeschlagen wurde, kann alternativ auch anstelle eines EOMs ein Magnetooptischer Modulator zur Frequenzverschiebung verwendet werden. Da dieser zur
Erzeugung der Frequenzverschiebung einen weiteren BLS Streuprozesse verwendet,
haben in diesem Fall Referenz- und Messsignal die gleiche Polarisation [A10].
Verwendet man die bereits vorgestellte Ortsauflösung, können die Phasenfronten
gemessen werden. Abbildung 3.9 zeigt ein Beispiel für eine phasenaufgelöste Messung. Dargestellt sind eine ortsaufgelöste (Abb. 3.9(a)) und eine phasenaufgelöste
(Abb. 3.9(b)) Messung an einer Spinwelle in einer YIG–Probe mit einer 20 µm breiten Lücke (senkrecht zur Propagationsrichtung). Die Anregung der Spinwelle erfolgt mit einer Mikrowellenantenne am linke Rand des Messbereichs. Während ein
kleiner Teil der Spinwelle durch die Lücke tunneln kann, wird der größere Anteil
reflektiert, wodurch sich eine stehende Welle ausbildet. In der ortsaufgelöste Messung ist diese stehende Welle deutlich sichtbar. Die phasenaufgelöste Messung (die
zeitlich vor der Reflexion an der Lücke durchgeführt wurde) zeigt die Phasenfronten
der einlaufenden Welle. Vergleicht man beide Messungen, so erkennt man, dass der
Abstand zwischen den Maxima in Abb. 3.9(a) (ortsaufgelöste Messung einer stehende Welle, d.h. die Periode ist λ /2) wie zu erwarten war nur halb so groß ist wie in
Abb. 3.9(b) (phasenaufgelöste Messung einer propagierenden Welle, d.h. die Periode ist λ ). Die gezeigte Messung bestätigt damit, dass die hier vorgestellte Technik
zur Visualisierung von Phasenfronten eingesetzt werden kann.
Abbildung 3.10 zeigt, dass die phasenaufgelöste BLS auch für quantitative pha-
3.5 Phasenaufgelöste Brillouin–Lichtstreuspektroskopie
39
7,18
1831 Oe
ν = ω /2π [GHz]
7,16
7,14
7,12
1821 Oe
7,10
7,08
8 mm
7,06
0
50
100
150
k [cm−1 ]
200
250
300
Abbildung 3.10: Dispersionskurve für Backward–Volume–Wellen gemessen mit der phasenaufgelösten BLS. Die gestrichelte Kurve beschreibt den theoretischen Verlauf der Dispersionskurven (vgl. Gl. (2.70)).
senaufgelöste Messungen eingesetzt werden kann. In den dargestellten Messungen
wurde für verschiedene Frequenzen und Magnetfelder die Wellenlänge λ und damit
der Wellenvektor k = 2π/λ der angeregten Spinwelle gemessen. Wie deutlich zu
erkennen ist, entsprechen die gemessenen Frequenz–Wellenvektor–Paare den theoretisch erwarteten.
In Kombination mit der Zeitauflösung können die so genannten Phasenprofile
bestimmt werden. Darunter versteht man den zeitabhängige Phasenunterschied zwischen der Spinwelle an einem definierten Ort und dem Mikrowellenpuls, der diese
Welle angeregt hat. Zur Messung dieses Profils ist es nötig, zwei Interferenzbilder
mit Referenzsignalen verschiedener Phase zu messen und diese in geeigneter Weise
mit einer nicht phasenaufgelösten Messung der Spinwelle und des Referenzsignals
zu kombinieren. Einen genaue Beschreibung dieser Technik findet sich in Anhang B.
Kapitel 4
Phasenaufgelöste Untersuchung der
Anregung und Propagation von
Spinwellen in YIG–Wellenleitern
Die Untersuchung von Spinwellen in YIG–Wellenleitern hat in den letzten Jahren
sowohl im Bereich der linearen wie auch der nichtlinearen Spinwellen zu neuen Erkenntnissen geführt. Exemplarisch seien hier die Beobachtung des Tunnelns von
Spinwellen durch einen Bereich mit lokal geändertem Feld [106] sowie durch eine
mechanische Lücke [A1], die Untersuchungen von Spinwellen–Solitonen [32–35],
die Interaktion von Spinwellen mit parametrischem Pumpen [A4] und die Entdeckung der symmetriebrechenden “Moebius”–Solitonen [41, 42] genannt. Insbesondere die letztgenannte Untersuchung wäre ohne die Kenntnis des Phasenprofiles der
Spinwellen (in diesem Experiment durch Interferenz zwischen Mikrowellensignalen
gewonnen) nicht möglich gewesen. Während die Mikrowellentechnik nur die Phaseninformationen am Ort der Antenne liefern kann, ermöglicht die phasenaufgelöste
BLS dies an beliebigen Orten der Probe. Damit war es im Rahmen dieser Arbeit
erstmals möglich, die Änderung der Phase mit der Propagationsdistanz (die sogenannte Phasenakkumulation) zu beobachten und damit das Verständnis linearer und
nichtlinearer Spinwellenphänomene zu erweitern.
Zunächst soll im Folgenden das Verfahren anhand von Messungen an linearen
Spinwellen vorgestellt werden (Kapitel 4.1). Anschließend wird mit dieser Technik
die Phasensymmetrie bei der Anregung von Spinwellen in verschiedenen Geometrien (Kapitel 4.2) und die Auswirkung der Nichtlinearität von Spinwellen auf die
Phase (Kapitel 4.3) untersucht.
42
Anregung und Propagation von Spinwellen
4.1 Propagation linearer Spinwellen
In diesem Kapitel soll das Phasenprofil und die Phasenakkumulation von linearen
Spinwelle untersucht werden. Dieser Fall wurde ausgewählt, um diese neue Messtechnik zunächst an einem einfachen System zu testen und vorzustellen, bevor dann
im weiteren Verlauf dieser Arbeit komplexere Fragestellungen untersucht werden.
Die entsprechenden Messungen wurden an mikrowellenangeregte Spinwellen in
einem YIG–Wellenleiter durchgeführt. Die lange Achse des Wellenleiters, welche
der Propagationsrichtung entspricht, war dabei parallel zum angelegten Feld ausgerichtet; es wurden daher Backward–Volume–Wellen angeregt. Der Wellenvektor der Spinwelle konnte durch Änderung des angelegten Feldes beeinflusst werden
(vgl. Kapitel 2.6.4).
Anzumerken ist, dass bei der Anregung von Spinwellen in Wellenleitern im Allgemeinen auch Anteile von höheren Breitenmoden angeregt werden. Diese führen
zu einer leichten Oszillation der Spinwelle entlang der Breite des Wellenleiters und
damit auch zu einer leichten Oszillation der Phase, die in einigen der nachfolgenden
Messungen zu erkennen ist. Dies hat allerdings keinen Einfluss auf die gewonnenen
Resultate.
4.1.1 Phasenprofil einer linearen Spinwellen
Abbildung 4.1 zeigt ein typisches Beispiel für das Phasen- und Intensitätsprofil einer linearen, langen, das heißt quasi–monochromatischen Spinwelle. Das Phasenprofil zeigt dabei die Phasendifferenz als Funktion der Zeit zwischen der Spinwelle
und dem Mikrowellensignal, das zur Anregung verwendet wurde (vgl. Anhang B).
Da in dem hier behandelten Fall Dispersion und Nichtlinearität keinen Einfluss auf
den Puls haben, behält dieser ein rechteckiges Intensitätsprofil (blaue Linie in der
Abbildung). Gleichzeitig erwartet man (in jedem Punkt der Propagation) ein zeitunabhängiges Phasenprofil, da der Puls näherungsweise als kontinuierliche Welle
beschrieben werden kann und die Phasendifferenz zwischen einer kontinuierlichen
Welle und ihrem anregenden Signal konstant ist. Auch dies wird durch die Messung
(rote Linie) bestätigt.
4.1.2 Lineare Phasenakkumulation
Um die ortsabhängige Änderung der Phase zu bestimmen, müssen mehrere Phasenprofile an verschiedenen Orten des Wellenleiters gemessen werden. Da hier ausschließlich die Phasenänderung entlang der Propagationsrichtung untersucht werden
sollte, wurden nur Phasenprofile entlang der Längsachse des Wellenleiters gemessen.
4.1 Propagation linearer Spinwellen
43
0,5
0,5
0,0
0,0
-0,5
-0,5
Phase [π]
1,0
-1,0
350
400
450
500
550
Intensität [a.u.]
1,0
-1,0
600
Zeit [ms]
Abbildung 4.1: Phasen- (rot) und Intensitätsprofil (blau) einer langen (das heißt
quasi–monochromatischen), linearen Backward–Volume–Welle.
(H0 = 1840 Oe,
ω = 2π · 7,132 GHz, Pulslänge τ = 200 ns).
0
Messpunkte
ϕ = − 2π
λ z + ϕ0
Fit: λ = 0,32 mm
-10
0,32 mm
Inteferenz
Intensität [a.u.]
Phase [π]
-5
-15
0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5
-20
z [ms]
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
z [mm]
Abbildung 4.2: Phasenakkumulation einer linearen Backward–Volume–Welle. Inset: Interferenz Muster der phasenaufgelösten BLS entlang der Längsachse des YIG Wellenleiters.
(H0 = 1840 Oe, ω = 2π · 7,132 GHz)
44
Anregung und Propagation von Spinwellen
Abbildung 4.2 zeigt ein typisches Beispiel der Phasenakkumulation einer linearen Backward–Volume–Welle. Da die Spinwelle im Wellenleiter näherungsweise
als ebene Welle beschrieben werden kann, erwartet man eine lineare Änderung der
Phase mit der Propagationsdistanz z
ϕ = kz + ϕ0
.
(4.1)
Dabei ist |k| = 2π/λ der Wellenvektor und ϕ0 die (bedeutungslose) Anfangsphase. Für die hier untersuchten Backward–Volume–Wellen erwartet man weiter einen
negativen Wellenvektor k ≤ 0. Beides wird durch die Messung bestätigt. Aus einem Fit von Gl. (4.1) an die experimentellen Daten erhält man für die Wellenlänge
einen Wert von λ = 0,32 mm. Dieser Wert stimmt mit der Wellenlänge überein,
die man aus dem Interferenzmuster der phasenaufgelösten BLS (Inset in Abb. 4.2)
abschätzen kann und bestätigt damit die Gültigkeit des gewählten Ansatzes.
4.2 Phasensymmmetrie bei der Anregung von Spinwellen
Wie bereits bei der Herleitung der allgemeinen Dispersionsrelation dipolarer Spinwellen (Kapitel 2.6) erwähnt, gibt es fundamentale Unterschiede zwischen Backward–Volume– und Surface–Wellen. Während bei ersteren die dynamische Magnetisierung m harmonisch über die Dicke des Wellenleiters verteilt ist, ist sie bei
letzterer an einer der Oberflächen lokalisiert und fällt exponentiell nach innen ab.
Für die Untersuchung von Surface–Wellen ist dabei besonders interessant, dass sich
das Maximum der Verteilung von einer Seite auf die andere verschiebt, wenn die
Propagationsrichtung der Welle umgedreht wird. Diese Nicht–Reziprozität spielt
eine wichtige Rolle bei verschiedenen Spinwellenphänomenen im Zusammenhang
mit parametrischer [107, 108] und nichtlinearer Interaktion von gegenläufigen Wellen [109], wie zum Beispiel bei der Reflektion [35] und Anregung [32] von Spinwellen.
Am deutlichsten wird dieser Einfluss bei der Anregung von gegenläufig propagierenden Spinwellen durch eine Mikrowellenantenne. Werden (reziproke) Backward–Volume–Wellen angeregt, propagieren beide Wellen mit identischer Amplitude. Im Fall der (nicht–reziproken) Surface–Wellen wird diese Amplitudensymmetrie gebrochen und die Propagation in einer Richtung ist stark unterdrückt. Abbildung 4.3 verdeutlicht die unterschiedliche Amplitudensymmetrie anhand von ortsaufgelösten BLS Messungen für beide Wellentypen.
Im Rahmen dieser Arbeit wurde nun erstmals die Phasensymmetrie von mikrowellenangeregten Spinwellen untersucht. Als Maß für die Phasensymmetrie wird
4.2 Phasensymmetrie von Spinwellen
45
x
H0
z
y
Mikrowellen
-antenne
Mikrowellen
-antenne
H0
(a) Backward–Volume–Wellen
(b) Surface–Wellen
Abbildung 4.3: Ortsaufgelöste BLS Messungen der Intensität gegenläufig propagierender (a) Backward–Volume– und (b) Surface–Wellen etwa 40 ns nach ihrer Anregung.
((a) H0 = 1835 Oe, (b) H0 = 1835 Oe, ω = 2π · 7,132 GHz)
dabei die sogennante Anregungsphase (oder Excitation Phase) verwendet. Darunter versteht man den anfänglichen Phasenunterschied zwischen zwei gegenläufig
propagierenden Spinwellen, die von derselben Mikrowellenantenne angeregt werden. Diese Anregungsphase ist insbesondere dann wichtig, wenn Interferenz zwischen den gegenläufigen Wellen möglich ist, zum Beispiel in Ringresonatoren [110].
Auch bei nichtlinearer Wechselwirkung (zum Beispiel bei der Kollision von Solitonen [109] und bei nichtlinearen Spinwellenresonanzen [111]) muss die Anregungsphase berücksichtigt werden.
Abbildung 4.4 zeigt den experimentellen Aufbau zur Messung der Phasensymmetrie (und den bereits gezeigten ortsaufgelösten BLS Messungen). Die Spinwellen wurden in einem 5 µm dicken YIG–Wellenleiter durch eine 50 µm breite Mikrostreifenantenne angeregt. Die Längsachse des Wellenleiters war dabei entweder
parallel (Backward–Volume–Wellen, Abb. 4.4(a)) oder senkrecht (Surface–Wellen,
Abb. 4.4(b)) zum angelegten Feld ausgerichtet. Die Intensität der anregenden Mikrowellenpulse wurde so gewählt, dass nur lineare Spinwellen angeregt werden.
Zur Messung der Anregungsphase werden die Phasenakkumulationen der beiden
gegenläufigen Spinwellen gemessen, linear gefittet und anschließend bis zum Ort der
Anregung, das heißt der Mitte der Antenne, extrapoliert. Die phasenaufgelösten BLS
Messungen sind notwendig, da eine Detektion des Phasenunterschieds mit konventioneller Mikrowellentechnik aufgrund der Symmetrie von Anregungs- und Detektionsprozess prinzipiell nicht möglich ist, da die Detektion einer Spinwelle mit Hilfe
einer Mikrowellenantenne zu einer zusätzlichen Phasenverschiebung führt. Diese ist
46
Anregung und Propagation von Spinwellen
x
H0
y
z
hq
IG
G
YI
Mikrowellen
-antenne
Y
Mikrowellen
-antenne
hq
H0
(a) Backward–Volume–Wellen
(b) Surface–Wellen
Abbildung 4.4: Experimenteller Aufbau zur Messung der Anregungsphase. Spinwellen werden mit Hilfe einer Mikrowellenantenne angeregt.
genauso groß wie die Anregungsphase hat allerdings das umgekehrte Vorzeichen.
Die Phasendifferenz zwischen den beiden detektierten Mikrowellensignalen ist daher unabhängig von der Anregungsphase.
4.2.1 Phasensymmetrie von Backward–Volume–Wellen
Experimentelle Resultate
Abbildung 4.5 zeigt ein typisches Beispiel für eine Messung an einer Backward–
Volume–Welle. Wie schon in Kapitel 4.1 beobachtet, erkennt man auch hier, dass die
Phase mit der Propagationsdistanz linear abnimmt. Mit Hilfe einer mikroskopischen
Aufnahme der Antenne und des Substrats (Inset in Abb. 4.5) kann die Position der
Antenne identifiziert und anschließend, wie oben beschrieben, die Anregungsphase
bestimmt werden. Im gezeigten Beispiel ergibt sich ein Wert von ∆ ϕ = (1,1 ±0,4)π.
Weitere Messungen bei verschiedenen magnetischen Feldern (das heißt verschiedenen Wellenvektoren der Spinwelle) bestätigten eine Anregungsphase von π für
Backward–Volume–Wellen (siehe Abb. 4.8). Sie werden demzufolge symmetrisch
in der Amplitude aber unsymmetrisch in der Phase angeregt.
Modell der Anregung
Der beobachtete Phasenunterschied kann anschaulich verstanden werden, wenn man
die Verteilung der dynamischen Magnetisierung m und des Feldes der Mikrowellenantenne hq berücksichtigt. Verwendet man das in Abb. 4.4(a) gegebene Koordinatensystem, liegt m in der x–y–Ebene, während hq nur Komponenten in x und z
Richtung hat. Demzufolge kann nur die x–Komponente von hq an die dynamische
4.2 Phasensymmetrie von Spinwellen
47
12
∆ ϕ = (1,1 ± 0,4)π
11
10
9
8
7
ϕ [π]
6
5
Mikrowellen
Antenne
4
3
YIG
2
1
0
-1
-2
-3
-4
-2,0
-1,5
-1,0
-0,5
0,0
0,5
1,0
1,5
2,0
z [mm]
Abbildung 4.5: Typisches Beispiel der Phasenakkumulation von gegenläufigen Backward–
Volume–Wellen. Das Inset zeigt eine mikroskopische Aufnahme des Substrats, die
zur Identifizierung der Antennenposition dient [79]. Als Anregungsphase ergibt sich
∆ ϕ = (1,1 ± 0,4)π. (H0 = 1835 Oe, ω = 2π · 7,132 GHz, k = (−198 ± 1)cm−1 )
Magnetisierung koppeln und eine Spinwelle anregen. Da diese Komponente antisymmetrisch in Bezug auf die Achse der Mikrowellenantenne (x = 0) ist, führt dies
zu einem Phasenunterschied von π für die beiden gegenläufigen Wellen.
Theoretische Beschreibung1
Mathematisch kann der Zusammenhang zwischen m, hq und dem dynamischen
Streufeld hs mit Hilfe des Polder–Suszeptibilitäts–Tensor (2.3) als
m = χ̂ · (hq + hs )
(4.2)
dargestellt werden. Zur vereinfachten Beschreibung der Anregung werden im Folgenden Magnetisierung und Felder über die Filmdicke d gemittelt betrachtet. In
1 Die theoretische Beschreibung wurde von M. P. Kostylev (University of Western Australia, Craw-
ley WA, Australien) aufgrund der vorliegenden Experimente durchgeführt und wird hier zum besseren Verständnis der Resultate zusammengefasst wiedergegeben. Eine vollständige Darstellung der
Theorie findet sich in [A9].
48
Anregung und Propagation von Spinwellen
dieser Näherung kann das Streufeld der Spinwelle mit der quasi–ein–dimensionalen
Greenschen Funktion [112]
hs(s) =
Z+∞
−∞
Ĝ(s − s′ )m(s′)ds′
(4.3)
beschrieben werden, wobei s die Koordinate entlang der Ausbreitungsrichtung ist.
Da bei Backward–Volume–Wellen nur die out–of–plane Komponente des dynamische Streufelds relevant ist, und, wie bereits erwähnt, nur die out–of–plane Komponente von hq zur Anregung beitragen kann, reduziert sich Gl. (4.2) zu einer skalaren
Integralgleichung von mx , hq,x und der out–of–plane Komponente von Ĝ(s) (siehe [111]). Daraus folgend erhält man einen Ausdruck für mx
mx (±|z|) =
4πi
h∓|k|,q,x ei|kz|
d
,
(4.4)
wobei h∓|k|,q,x die Fourier–Transformierte von hq,x ist. Wie bereits erwähnt ist hq,x
antisymmetrisch in Bezug auf x = 0. Damit gilt für die Fourier–Transformierte
h−|k|,q,x = −h+|k|,q,x und somit mx (−|z|) = −mx (+|z|). Backward–Volume–Wellen
haben daher, wie im Experiment gezeigt, eine Anregungsphase von π und werden
symmetrisch in der Amplitude angeregt.
4.2.2 Phasensymmetrie von Surface–Wellen
Experimentelle Resultate
Abbildung 4.6 zeigt ein typisches Beispiel für eine Messung an einer Surface–Welle.
Im Gegensatz zu den Messungen an Backward–Volume–Wellen (siehe Kapitel 4.1
und 4.2.1) nimmt hier die Phase mit der Propagationsdistanz linear zu, da bei Surface–Wellen Wellenvektor und Gruppengeschwindigkeit dieselbe Richtung haben.
Für die Anregungsphase im gezeigten Beispiel ergibt sich ∆ ϕ = (0,16 ± 0,17)π.
Weitere Messungen mit verschiedenen Wellenvektoren bestätigen eine Anregungsphase von Null für Surface–Wellen (siehe Abb. 4.8). Sie werden demzufolge unsymmetrisch in der Amplitude aber symmetrisch in der Phase angeregt.
Modell der Anregung
Im Gegensatz zum Fall der Backward–Volume–Wellen liegen bei den Surface–Wellen m und hq in derselben Ebene; die Beschreibung der Anregung wird dadurch
deutlich komplexer. Um trotzdem eine einfaches Modell der Anregung zu erhalten,
4.2 Phasensymmetrie von Spinwellen
49
5,0
4,5
4,0
3,5
ϕ [π]
3,0
Mikrowellen
Antenne
2,5
2,0
YIG
1,5
1,0
0,5
0,0
∆ ϕ = (0,16 ± 0,17)π
-0,5
-1,0
-2,0
-1,5
-1,0
-0,5
0,0
0,5
1,0
1,5
2,0
y [mm]
Abbildung 4.6: Typisches Beispiel der Phasenakkumulation von gegenläufigen Surface–
Wellen. Das Inset zeigt eine mikroskopische Aufnahme des Substrats [79]. Als Anregungsphase ergibt sich ∆ ϕ = (0,16 ± 0,17)π. (H0 = 1825 Oe, ω = 2π · 7,132 GHz,
k = (75 ± 1)cm−1 )
ist es sinnvoll die in–plane Komponente hq,y und die beiden out–of–plane Komponenten hq,x,y>0 und hq,x,y<0 von hq getrennt zu betrachten und anschließend die drei
“Teilwellen” zu überlagern.
Abbildung 4.7 verdeutlicht den Ansatz. Zur Vereinfachung sei angenommen,
dass die Breite der Antenne der halben Wellenlänge entspricht. Betrachtet man
zunächst die Welle, die von der in–plane Komponente hq,y angeregt wird (dargestellt
in Abb. 4.7(a)), so erkennt man, dass der Teil der Welle, der entlang der positiven
y–Richtung läuft, die Kante der Antenne in Phase mit dem dort existierenden out–
of–plane Feld erreicht. Dieser Teil der Welle wird daher nicht an der Ausbreitung
gehindert. Die Welle, die in negativer Richtung läuft, ist dagegen außer Phase mit
hq,x,y<0 und wird demzufolge stark abgeschwächt. Ähnlich verhält es sich mit der
Teilwelle, die von hq,x,y>0 angeregt wird (Abb. 4.7(b)). Nur die Welle in positiver
Richtung kann propagieren, während die Welle in negativer Richtung außer Phase
mit hq,y ist und daher stark abgeschwächt wird. Die letzte der drei Teilwellen, die
von hq,x,y<0 angeregt wird (Abb. 4.7(c)), kann in beide Richtungen frei propagieren,
da der in positiver Richtung laufende Teil in Phase mit hq,y und hq,x,y>0 ist.
50
Anregung und Propagation von Spinwellen
w = λ /2
x
y
hq,x,y<0
Antenne
hq,x,y>0
hq,y
m(t)
k
(a) 1. Teilwelle
(b) 2. Teilwelle
(c) 3. Teilwelle
Abbildung 4.7: Modell der Anregung von Surface–Wellen. Betrachtet man die drei Komponenten von hq getrennt, so erkennt man, dass nur die Welle entlang der positiven Richtung
mit nennenswerter Intensität propagieren kann.
Addiert man alle drei Teilwellen, erkennt man leicht, dass die Propagation in
negativer Richtung deutlich unterdrückt ist und damit die Surface–Welle unsymmetrisch in der Amplitude angeregt wird. Möchte man mit diesem Modell die beobachtete Phasensymmetrie erklären, so ist zu beachten, dass aufgrund der Größe der
Antenne im Vergleich zur Filmdicke (Breite der Antenne: 50 µm, Dicke des Films:
Dicke 5 µm) das in–plane Feld deutlich stärker zur Anregung beiträgt als das out–
of–plane Feld. Gleichzeitig ist aufgrund der Elliptizität der Spinwelle die out–of–
plane Komponente von m kleiner als die in–plane–Komponente. Daher bestimmt
hauptsächlich die erste Teilwelle den Phasenunterschied der beiden gegenläufigen
Wellen, so dass dieser, wie im Experiment beobachtet, Null ist.
Theoretische Beschreibung2
Wie zu erwarten, ist auch die theoretische Beschreibung der Anregung von Surface–
Wellen deutlich komplexer. Da m, hq und hs in derselben Ebene liegen, müssen alle
Komponenten von hq und hs in Gl. (4.2) berücksichtigt werden. Die diagonalen und
2 Die
in [A9].
von M. P. Kostylev entwickelte, vollständige theoretische Beschreibung findet sich wieder
4.2 Phasensymmetrie von Spinwellen
51
nicht–diagonalen Terme von χ̂ mischen daher. Das Ergebnis dieser Vermischung ist
kompliziert und kann orts- und wellenvektorabhängig sein, da
1. die Nichtdiagonalelemente von χ̂ im Vergleich zu den Diagonalelementen um
±π/2 phasenverschoben sind;
2. unterhalb der Filmoberfläche hq,y überall die gleiche Phase hat, aber hq,x bei
der Antennenachse y = 0 einen Phasensprung um π erfährt; und
3. die verschiedenen Komponenten der Greenschen Funktion in Gl. (4.3) in verschiedener Weise vom Spinwellenwellenvektor abhängen (siehe zum Beispiel
[113]).
Mit Hilfe derselben Methode, die auch in [A6] verwendet wurde, erhält man für
die dynamische Magnetisierung
m(y) =
Z+∞
−∞
Ĝexc (y − y′ )hq (y′ )dy′
,
(4.5)
1
Ŷ F(y − y′ )
D(k)
.
(4.6)
mit
Ĝexc (y − y′ ) =
Dabei ist
D(k) =
d
[W (k)(W (k) + 1)]
d(|k|)
(4.7)
und
i
1 h
−ik|s|
−ik|s|
ik|s|
F(s) =
−2πie
+e
E1 (−ik|s|) + e E1 (ik|s|)
,
(4.8)
2π
wobei E1 die Integralexponentialfunktion (siehe zum Beispiel [114]), k der Wellenvektor und d die Filmdicke sind. Für die Matrix Ŷ erhält man
Y11 = −W (k) − 1 +
Y21 = −
iκ
(κ 2 − χ 2 )
χ
(κ 2 − χ 2 )
Y12 =
iκ
(κ 2 − χ 2 )
Y22 = W (k) +
χ
(κ 2 − χ 2 )
(4.9)
mit
W (k) = (exp(− |k| d) − 1) /(|k| d) .
(4.10)
1
Anhand dieser Gleichungen erkennt man, dass der Ausdruck D(k)
Ŷ · hq den anfänglichen Wert der Phase (und damit die Anregungsphase) bestimmt, während F(s)
52
Anregung und Propagation von Spinwellen
(Gl. (4.8)) die Phasenakkumulation beschreibt. Weit weg von der Antenne verschwinden in dieser Gleichung die Terme, die die Integralexponentialfunktion E1 (s)
enthalten und es bleibt
F(s) = −ie−i|ks| .
(4.11)
Betrachtet man den hier vorliegenden Grenzfall kleiner Wellenvektoren (kd ≪ 1)
kann die Exponentialfunktion in Gl. (4.7) als Potenzreihe genähert werden. Dadurch
ergibt sich
|k|d
W (k) ≈ −1 +
.
(4.12)
2
Damit vereinfacht sich Ŷ zu
Y11 = −
1
Y12 =
(κ 2 − χ 2 )
iκ
Y21 = − 2
(κ − χ 2 )
iκ
(κ 2 − χ 2 )
(χ + 1)2 − κ 2
Y22 =
(κ 2 − χ 2 )
(4.13)
und Gl. (4.7) zu D(k) = d/2. Gleichung (4.5) liefert damit
m(±|y|) = −2πi
2Ŷ −i|ky|
e
h±|k|,q
d
(4.14)
wobei h±|k|,q die Fourier–Transformierte des Antennenfeldes ist. Aus den Maxwell Gleichungen ergibt sich für das magnetische Feld eines Mikrostreifenleiters
hk,q,x = i sign(k)hk,q,y (siehe zum Beispiel Gl. (32) in [115]). Bei Surface–Wellen
gilt sign(k) = sign(y), daher kann h±|k|,q als
h±|k|,q =
i sign(y)
1
h|k|,q,y
(4.15)
dargestellt werden.
Da sich mx und my nur durch eine Phasenverschiebung von π/2 und den Faktor
der Elliptizität unterscheiden, ist es für die weitere Betrachtung ausreichend, nur eine
Komponente von m zu betrachten. Aus Gl. (4.14) und (4.15) ergibt sich für mx
mx (±|y|) =
κ − sign(y) −i|ky|
4π
h|k|,q,y 2
e
d
κ − χ2
.
(4.16)
Für den gesamten Frequenzbereich von Surface–Wellen (Gl. (2.66)) ist κ < −1,
das heißt, der Koeffizient vor der Exponentialfunktion hat überall dasselbe Vorzeichen. Surface–Wellen haben daher, wie im Experiment gezeigt, eine Anregungsphase von Null. Gleichzeitig erkennt man anhand des Ausdrucks κ − sign(y) das die
4.2 Phasensymmetrie von Spinwellen
53
2,0
∆ ϕ [π]
1,5
1,0
0,5
BVMSW
MSSW
0,0
-0,5
-300
-250
-200
-150
-100
-50
Wellenvektor [cm−1 ]
0
50
100
Abbildung 4.8: Zusammenfassung der durchgeführten Messungen. Eine Anregungsphase
von π für Backward–Volume–Wellen und von Null für Surface–Wellen ist deutlich sichtbar.
Die Abweichungen für die jeweils betragsmäßig geringsten Wellenvektoren kann durch die
Störung der Propagation nahe der oberen beziehungsweisen unteren Grenzfrequenz des jeweiligen Spinwellen–Bands erklärt werden. Die Hauptursache der Messfehler ist die ungenaue Kenntnis der Antennenposition. Da der Positionsfehler ∆ x gemäß k∆ x zum Fehler der
Anregungsphase beiträgt, steigt dieser mit größer werdendem Betrag des Wellenvektors.
Amplitude für die Propagation in positive y–Richtung immer größer ist, als in negative y–Richtung, so dass die Gleichung auch die Asymmetrie der Amplitude von
Surface–Welle bestätigt.
Vergleicht man das hier gewonnenen Ergebnis mit dem korrespondierenden Gleichung für Backward–Volume–Wellen (Gl. (4.4)), so fällt auf, dass hier das Vorzeichen des komplexen Exponenten negativ ist. Dies hat zur Folge, dass wie im Experiment beobachtet, die Phasenakkumulation bei Backward–Volume–Wellen monoton
fallend und bei Surface–Wellen monoton steigend ist.
54
Anregung und Propagation von Spinwellen
4.3 Einfluss der Nichtlinearität auf die Phase der
Spinwellen
Während im bisherigen Verlauf dieses Kapitels nur lineare Spinwellen untersucht
wurden, soll jetzt eine nichtlineare Beeinflussung der Phase vorgestellt werden. Die
Annahmen |m| ≪ |M0 | und Mz ≈ MS gelten daher nicht mehr, und Mz wird abhängig von m:
q
MS2 − |m|2
Mz =
.
(4.17)
Abbildung 4.9(a) veranschaulicht diesen Sachverhalt. In erster Näherung kann
die Verringerung von M
qz berücksichtigt werden, indem in der jeweiligen Dispersi-
onsrelation MS durch MS2 − |m|2 ersetzt wird. Dies führt im Vergleich zur lineraren Dispersion zu einer Stauchung entlang der Frequenzachse (vgl. Abb. 4.9(b)
und Kapitel 2.6.4), das heißt bei gleicher Frequenz hat eine Spinwelle mit höherer
Amplitude einen (betragsmäßig) geringeren Wellenvektor. Da die Spinwellenphase
durch den Wellenvektor beeinflusst wird, sollte es daher einen direkten Einfluss der
Spinwellenamplitude auf die Phase geben.
4.3.1 Phasenprofil einer nichtlinearen Spinwelle
m
MS
Mz
β
(a) Änderung von Mz
H0
Frequenz ν = ω /2π [GHz]
Zur Untersuchung dieses Einflusses wurden, wie bereits bei der Untersuchung der
linearen Phasenakkumulation, lange Spinwellenpulse, die parallel zum Feld propaMz = q
MS
7,2
Mz =
MS2 − |m|2
ν = 7,132 GHz
7,1
7,0
0
100
200
300
400
500
Wellenvektor [cm−1 ]
(b) Änderung der Dispersion
Abbildung 4.9: (a) Zusammenhang zwischen dem Präzessionswinkel β , m, MS und Mz .
Für große
q Amplituden m verliert Mz ≈ MS seine Gültigkeit. Stattdessen erhält man
Mz = MS2 − |m|2 . (b) Verschiebung der Dispersionsrelation bei großer Spinwellenamplitude.
4.3 Einfluss der Nichtlinearität auf die Phase der Spinwellen
55
0,5
0,5
0,0
0,0
-0,5
-0,5
Phase [π]
1,0
Intensität [a.u.]
1,0
-1,0
-1,0
400
450
500
550
600
Zeit [ns]
Abbildung 4.10: Phasen- und Intensitätsprofil einer nichtlinearen Backward–Volume–
Wellen. (H0 = 1840 Oe, ω = 2π · 7,132 GHz, Pulslänge τ = 200 ns)
gieren, verwendet. Die Intensität der zur Anregung verwendeten Mikrowellenpulse
wurde allerdings im Vergleich zur linearen Messung erhöht, so dass eine deutliche
Verringerung von Mz auftrat und nichtlineare Prozesse möglich wurden.
Einer dieser Prozesse ist die sogenannte Vier–Magnonen–Wechselwirkung, die
zu einem nichtlinearen Zerfall der Spinwelle führt. Für die weitere Untersuchung ist
dabei besonders wichtig, dass dieser Effekt eine relative lange Zeit benötigt, um sich
zu entwickeln [116].
Dies führt zur Ausbildung eines Intensitätsprofils mit einem ungedämpften Peak
am Anfang des Pulses und einem flachen Rücken, der durch die Vier–Magnonen–
Wechselwirkung beeinflusst wurde und daher eine deutlich geringere Intensität aufweist. Die blaue Kurve in Abb. 4.10 zeigt ein typisches Beispiel dieses Profiles.
Wie bereits erwähnt gibt es einen direkten Einfluss der Spinwellenintensität auf den
Wellenvektor und damit auf die Phase. Das gemessene Phasenprofil (rote Kurve in
Abb. 4.10) zeigt diesen deutlich. Während die Phase im Bereich des Rückens nahezu konstant ist, kann im Bereich des Peaks und des Übergangs zwischen Peak
und Rücken (das heißt in den Bereichen, in denen sich die Intensität ändert) eine
Änderung der Phase beobachtet werden.
4.3.2 Nichtlineare Phasenakkumulation
Abbildung 4.11 zeigt Beispiele für die Phasenakkumulation eines langen, nichtlinearen Spinwellenpulses sowohl für die Phase des Peaks wie auch für die Phase des
Rückens. Zum Vergleich mit dem linearen Fall ist ebenfalls der Fit aus Abb. 4.2 ein-
56
Anregung und Propagation von Spinwellen
0
-5
Phase [π]
-10
-15
(a)
Phase am Peak des Pulses
-20
Phase am Rücken des Pulses
(b)
Fit der linearen Messung
-25
-30
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
z [mm]
Abbildung 4.11: Phasenakkumulation von nichtlinearen Backward–Volume–Wellen.
((a) H0 = 1840 Oe, (b) H0 = 1850 Oe, ω = 2π · 7,132 GHz, Spinwellenintensität vergleichbar
in beiden Fällen.)
gezeichnet. Die dem Fit zugrundeliegende Messung wurde mit den gleichen Werten
für H0 und ω durchgeführt, die auch bei Messung (a) in Abb. 4.11 verwendet wurden.
Wie bereits beim Phasenprofil in Abb. 4.10 ist die Phase des Peaks (das heißt des
Bereichs mit hoher Intensität) auf der gesamten Propagationsdistanz deutlich größer
als die Phase des Rückens. Der Vergleich mit dem Fit der linearen Spinwelle zeigt,
dass die Intensität des Rückens nicht groß genug ist, um eine nennenswerte Änderung von Mz zu erzeugen und der Rücken somit als lineare Spinwelle beschrieben
werden kann.3
Betrachtet man die Differenz der Phasen von Rücken und Peak als Funktion
der Propagationsdistanz z (siehe Abb. 4.12), erkennt man, dass ihr Betrag bis zu
einem (feldabhängigen) Maximalwert ansteigt und danach (ab ca. z = 2,5 mm) konstant bleibt.4 Ursache hierfür ist die Dämpfung der Spinwelle. Während der Propagation wird die Intensität der Spinwelle reduziert und damit Mz im Bereich des
3 Die Abweichung am Ende der Propagation können durch das geringe Signal–zu–Rausch Verhält-
nis im Vergleich zur linearen Messung erklärt werden.
4 Die Phasendifferenz ist dabei negativ, da die Phase des Peaks größer ist als die Phase des
Rückens.
4.3 Einfluss der Nichtlinearität auf die Phase der Spinwellen
57
-0,1
-0,2
-0,3
(a)
∆ ϕ [π]
-0,4
-0,5
-0,6
-0,7
-0,8
(b)
-0,9
0,0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
4,0
4,5
z [mm]
Abbildung 4.12:
Differenz zwischen der Phase des Rückens und des Peaks.
((a) H0 = 1840 Oe, (b) H0 = 1850 Oe, ω = 2π·7,132 GHz, Spinwellenintensität vergleichbar
in beiden Fällen.)
Peaks erhöht. Das führt dazu, dass der Betrag des (Peak–)Wellenvektors während
der Propagation kontinuierlich ansteigt, bis er schließlich (wenn auch für den Peak
Mz ≈ MS gilt) gleich dem linearen (Rücken–)Wellenvektor ist. Interpretiert man die
Ableitung der Phase ϕ als Wellenvektor k, wie es im Fall einer ebenen Welle gelten
würde (vgl. Gl. (4.1)) und damit die Ableitung der Phasendifferenz ∆ ϕ als Wellenvektordifferenz ∆ k, so erkennt man, dass die Messungen in Abb. 4.12 diesen Effekt
bestätigen.
Die Messung von ∆ ϕ kann in Kombination mit der Dispersionsrelation (2.70)
zur Berechnung der Dämpfungszeit, das heißt die Zeit nach der sich die Amplitude
der Spinwelle auf 1/e ihres anfänglichen Werts reduziert hat, und des Präzessionswinkels (vgl. Abb. 4.9(a)) verwendet werden, wie folgende Überlegung zeigt. Für
den linearen Rücken der Spinwelle gilt
|k| = |k|lin
Mz = MS
,
(4.18)
während für den nichtlinearen Peak Wellenvektor und statische Magnetisierung reduziert sind:
q
d(∆ ϕ )
|k| = |k|lin − ∆ k = |k|lin −
Mz = MS2 − |m|2 .
(4.19)
dz
58
Anregung und Propagation von Spinwellen
Da alle Parameter der Dispersionsrelation (2.70) bekannt sind (oder durch die gemessenen Daten des linearen Rückens bestimmt werden können), kann mit Hilfe
von Gl. (4.19) und (2.70) die dynamische Magnetisierung m(z) bestimmt werden.
Wird diese Rechnung für einen exponentiellen Fit der Daten für H = 1850 Oe
in Abb. 4.12 durchgeführt, so erhält man eine Dämpfungszeit von 140 ns und einen
anfänglichen Präzessionswinkel von 6◦ , beides sinnvolle Werte für nichtlineare Spinwellen in YIG.
Im bisher beschriebenen Ansatz sollte der Maximalwert von ∆ ϕ nur von der
anfänglichen Spinwellenintensität (und damit vom (extrapolierten) Wert ∆ k bei der
Anregung der Spinwelle) abhängen. Da in den hier gezeigten Messungen die Intensität der Spinwellen bei den verschiedenen Feldern vergleichbar gewählt wurde,
sollten also ∆ kinitial und ∆ ϕmax bei beiden Messungen identisch sein. Ersteres kann
im Rahmen der Messgenauigkeit durch exponentielle Fits der ∆ ϕ (z) Messungen
bestätigt werden. Der Maximalwert von ∆ ϕ ist allerdings deutlich vom angelegten
Feld abhängig (siehe Abb. 4.12).
Eine mögliche (qualitative) Erklärung ist der Einfluss von sekundären Spinwellen, die während der Propagation durch den Peak des Spinwellenpulses erzeugt werden. Ist die Gruppengeschwindigkeit dieser Wellen klein, bildet sich ein Gebiet mit
reduzierter Magnetisierung aus, durch das der Rücken des Pulses propagieren muss.
Dies würde zu einem betragsmäßig kleineren Wellenvektor des Rückens führen und
damit auch zu einem geringen Phasenunterschied zwischen Peak und Rücken. Wie
in der Arbeit von Damon und Eshbach [72] gezeigt ist, ist die Zustandsdichte für
Spinwellen mit geringer Gruppengeschwindigkeit nahe der oberen Grenzfrequenz
für Backward–Volume–Wellen besonders hoch. Die Anregung langsamer Spinwellen läuft daher für ein kleineres angelegtes Feld effektiver ab, da in diesem Fall die
Frequenz der propagierenden Welle näher an der oberen Grenzfrequenz liegt. Damit
sollte der Maximalwert des Phasenunterschieds wie beobachtet für kleinere Felder
sinken.
Kapitel 5
Anregung und Untersuchung von
Spinwellen–Kaustikstrahlen
Eine Gemeinsamkeit aller Arten von lateral begrenzten linearen Wellen ist ihre Eigenschaft, sich während der Propagation zu verbreitern.1 Diese Verbreiterung ist besonders ausgeprägt, wenn die anfängliche Ausdehnung der Welle vergleichbar oder
kleiner als ihre Wellenlänge ist. Nichtlineare Effekte, im Fall von Lichtwellen zum
Beispiel die Änderung des Brechungsindex n mit der Lichtintensität, können diese
Verbreiterung kompensieren und lateral stabile Strahlen erzeugen; man spricht von
räumlichen Solitonen. Die Erzeugung dieser Solitonen wurde zunächst bei Lichtwellen [40, 119], später auch bei Spinwellen beobachtet [120]. Bei beiden Systemen
muss zur Erzeugung der Solitonen die Intensität der Welle einen gegebenen Schwellenwert überschreiten, damit die Nichtlinearität stark genug ist, um die Verbreiterung
zu kompensieren. Da in allen realen Systemen Dämpfung auftritt, ist die Existenz
von Solitonen nur über beschränkte Distanzen möglich. Sobald die Intensität der
Welle aufgrund der Dämpfung den Schwellenwert unterschreitet, hört das Soliton
auf zu existieren und die Welle beginnt sich wieder zu verbreitern. Nichtlineare
Effekte können daher eine Welle nur über beschränkte Distanzen stabilisieren.
Eine Alternative zur Erzeugung von lateral beschränkten, stabilen Wellen verwendet die Anisotropie des Propagationsmediums. Dabei wird ausgenutzt, dass es
1 Theoretisch
existiert mit dem sogenannten Bessel–Strahl eine Klasse von, Wellen die sich nicht
verbreitert. Dieser bestehet aus einem lateral begrenzten, stabilen Strahl, der von unendlich vielen
schwachen, konzentrischen Ringen umgeben ist. Ein idealer Bessel–Strahl wäre damit, trotz des
lateral begrenzten Zentrums, unendlich ausgedehnt. Zu seiner Erzeugung wäre demnach unendlich
viel Energie notwendig, so dass experimentell nur eine Näherung erzeugt werden kann. Wie gezeigt
wurde, ist diese über beschränkte Distanzen lateral stabil [98, 117, 118].
60
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
in verschiedenen Systemen möglich ist, dass Wellen mit gleicher Frequenz aber verschieden gerichteten Wellenvektoren k in dieselbe Richtung propagieren. In diesem
Fall führen kleine Änderungen der Richtung des Wellenvektors nicht zu einer Änderung der Ausbreitungsrichtung. Da die Verbreiterung einer Welle im Allgemeinen
durch die unterschiedliche Ausbreitungsrichtungen ihrer verschiedenen Wellenvektorkomponenten verursacht wird, kann die beschriebene Anisotropie diesen Effekt
reduzieren oder sogar verhindern. Da die Anisotropie eines Materials nicht durch die
Intensität der propagierenden Welle beeinflusst wird, ist die Stabilität dieser Welle
nicht durch Dämpfung limitiert.
Neben der direkten Anregung von Wellen mit einem entsprechend gerichteten
Wellenvektor kann bei geeigneter Form der Abhängigkeit der Richtung der Gruppengeschwindigkeit von der Richtung des Wellenvektors auch die eigenständige Ausbildung von lateral stabilen Strahlen beobachtet werden. Im Gegensatz zu den direkt
angeregten Wellen, die einen klar definierten Wellenvektor haben, entstehen diese
aus der Interferenz vieler Wellen mit gleicher Frequenz aber verschieden gerichteten
Wellenvektoren. Erstmalig untersucht und erklärt wurde dieser Effekt bei Phononen, wo er durch die elastische kristallographische Anisotropie erzeugt wird [121].
Die Ausbreitungsrichtung der stabilen Welle wird in diesem Fall durch intrinsische
Materialparameter bestimmt und kann nicht von außen kontrolliert werden. Demgegenüber haben Spinwellen den Vorteil, dass die zur Anregung relevante Anisotropie durch das externe Magnetfeld induziert wird und damit kontrolliert werden
kann [53, 54].
Frühere Experimente mit Spinwellen konnten bereits Anzeichen von lateral stabilen Wellen in Form von Interferenzmustern nach der Streuung einer ebenen Welle
an einem Defekt beobachten. Aufgrund der fehlenden Kontrolle über Position und
Größe dieses Defekts sowie der Interferenz zwischen der ebenen Welle mit dem
gestreuten Anteil war eine genaue Untersuchung der Anregung nicht möglich. Die
direkte Anregung mit Hilfe einer Mikrostreifenantenne lieferte aufgrund der ungünstig gewählten Antenne ebenfalls nur schwache Anzeichen einer lateral stabilen Welle [104].
Im Folgenden soll nun gezeigt werden, dass eine kontrollierte Anregung dieser
lateral stabilen Wellen, der sogenannten “Kaustikstrahlen”, bei Spinwellen möglich
ist. Außerdem soll der Anregungsprozess untersucht werden. Die dazu notwendigen
experimentellen und theoretischen Grundlagen werden in Kapitel 5.1 besprochen.
Anschließend werden die im Rahmen dieser Arbeit gewonnenen Resultate vorgestellt. Diese beinhalten die Kontrolle der Kaustikanregung (Kapitel 5.2), die Untersuchung der Fein- und Phasenstruktur von Kaustikstrahlen (Kapitel 5.3 und 5.4)
sowie die Untersuchung ihrer Reflexion und Streuung (Kapitel 5.5).
5.1 Grundlagen der Kaustikanregung
61
5.1 Grundlagen der Kaustikanregung
5.1.1 Prinzip
Wie bereits in Kapitel 2.6.5 gezeigt wurde, ist die Abhängigkeit der Richtung der
Gruppengeschwindigkeit θ von der Richtung des Wellenvektors φ aufgrund der
durch das angelegte Feld induzierten Anisotropie nicht monoton. Insbesondere gibt
es (abhängig von den gewählten Propagationsparametern H0 und ω sowie den Materialeigenschaften MS und d) Bereiche, in denen θ nur schwach (oder gar nicht) von
φ abhängig ist und daher
θ (φ1 ≤ |φ | ≤ φ2 ) ≈ ±θK
(5.1)
gilt. Da für das hier betrachtete System dieses Plateau im Bereich 20◦ ≤ |φ | ≤ 40◦
liegt (siehe Abb. 5.1), werden die Auswirkungen dieses Effekts erst erkennbar, wenn
man die Anregung einer Spinwelle in einem weiten (Wellenvektor–)Winkelbereich
mit φmax ≥ 40◦ betrachtet.2
Die gesamte Amplitude, die innerhalb des in Gl. (5.1) genannten Bereichs abgestrahlt wird, trägt in diesem Fall aufgrund der speziellen Form der θ (φ )–Kurve zu einem Spinwellenstrahl entlang der θ = ±θK Richtung bei. Die Amplitude außerhalb
dieses Bereichs wird im W esentlichen homogen über die Ausbreitungsrichtungen
|θ | < |θK | verteilt. Als Resultat erhält man also zwei lateral begrenzte Spinwellenstrahlen entlang θ = ±θK , mit einer deutlich schwächeren homogenen Spinwelle im
Bereich dazwischen.
Abbildung 5.1 veranschaulicht diesen Effekt. Zur Vereinfachung wird dabei angenommen, dass die Spinwelle im Winkelbereich −45◦ < φ < 45◦ mit konstanter
Amplitude angeregt wird.
5.1.2 Experimentelle Realisierung
Wie bereits gezeigt wurde ist zur Anregung von Kaustikstrahlen eine Spinwellenantenne nötig, die in einem weiten Winkelbereich (|φmax | ≥ 40◦ ) abstrahlt. Da φmax
durch
ky,max
φmax = arctan
(5.2)
kz
2 Wie
in Abb. 2.6 zu erkennen ist, hat θ (φ ) ein weiteres Plateau im Bereich von φ ≈ ±70◦ . Die-
ses spielt allerdings für die experimentelle Untersuchung keine Rolle, da die räumliche Dämpfung
in diesem Bereich deutlich stärker ist als bei kleineren Werten von φ und daher die Propagation von
Spinwellen stark unterdrückt ist. Unabhängig davon ist es mit den hier verwendeten Antennen außerdem nicht möglich, Spinwellen mit derart großen Wellenvektorwinkeln anzuregen.
62
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
40
θ [◦ ]
20
0
-20
-40
Ak ( φ )
0
1
k
0
-60
φ
-40
-20
0
φ [◦ ]
20
40
60
1
Amplitude [a.u.]
vp
vg
θ
H0
Abbildung 5.1: Prinzip der Kaustikanregung. Aufgrund der speziellen Form der θ (φ )–
Kurve, wird die gesamte im Bereich 30◦ ≤ |φ | ≤ 40◦ abgestrahlte Amplitude zu Strahlen
entlang θ = ±θK gebündelt.
gegeben ist, muss also zur Anregung von Kaustikstrahlen der Trägerwellenvektor
in z–Richtung kz klein und die maximale Wellenvektorkomponente in y–Richtung
ky,max groß sein. Während der Trägerwellenvektor kz durch die Dispersionsrelation
bestimmt ist und durch Wahl von Frequenz ω und Magnetfeld H0 geeignet gewählt
werden kann, hängt ky,max nur von der Breite w der Antenne ab. Dabei gilt (siehe
auch Gl. (5.7))
ky,max ∼ w−1 .
(5.3)
Zur Anregung von Kaustikstrahlen wird daher eine möglichst schmale Antenne benötigt. Schätzt man anhand von Gl. (5.2) und (5.3) den maximal möglichen Wert
von w für Spinwellen in YIG ab, so ergibt sich eine maximale Antennenbreite von
deutlich unter einem Millimeter. Diese kann nicht mehr mit einer gewöhnlichen
Mikrostreifenantenne realisiert werden.
Hier wurde daher für die Untersuchung der Kaustikstrahlen die bereits in Kapitel 3.2 beschriebene Wellenleiterantenne verwendet. Abbildung 5.2 zeigt das Anregungsspektrum Ak für verschieden Wellenleiterantennen (auf die Berechnung dieser
Spektren wird im nächsten Abschnitt eingegangen). Wie zu erkennen ist, ist das
Spektrum der Antenne breit genug, um Kaustikstrahlen anzuregen.
Abbildung 5.3 zeigt ein typisches Beispiel einer ortsaufgelösten BLS–Messung
5.1 Grundlagen der Kaustikanregung
63
Anregungsspektrum Ak [a.u.]
1,0
w = 400 µm
w = 500 µm
w = 750 µm
0,8
0,6
0,4
0,2
w
0,0
-0,2
-60
-40
-20
0
φ [◦ ]
20
40
60
Abbildung 5.2: Spektrum der verwendeten Wellenleiterantennen. Wie deutlich zu erkennen
ist, können Spinwellen bis zu einem Wellenvektorwinkel φmax ≈ 40◦ angeregt werden. Die
Antenne kann damit zur Anregung und Untersuchung von Spinwellen–Kaustikstrahlen verwendet werden. (H0 = 1840 Oe, ω = 2π · 7,132 GHz)
einer Kaustikanregung. Dargestellt ist eine Falschfarbendarstellung der gemessenen
Spinwellenintensität im Eingangswellenleiter und der Propagationsfläche. Wie erwartet wirkt der Übergang vom Wellenleiter zur Propagationsfläche wie eine (schmale) Antenne, die zwei klar definierte Kaustikstrahlen anregt. Diese propagieren frei
und bleiben, wie deutlich zu erkennen ist, trotz der Reflexion an den rauen Rändern
der Probe für mehr als 10 mm lateral stabil.
5.1.3 Numerische Berechnung
Zur Simulation der (stationären) Kaustikstrahlen kann das Huygenssche Prinzip (siehe zum Beispiel [98]) verwendet werden. Dabei wird die Propagation einer Welle
durch die phasenrichtige Addition aller angeregten Elementarwellen beschrieben.
Zur Vereinfachung der Rechnung wird diese Addition hier im k–Raum durchgeführt.
Die Elementarwellen können in diesem Fall als ebene Wellen der Form
Ak (k)eir·k
dargestellt werden.
(5.4)
64
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
10 mm
Abbildung 5.3: Falschfarbendarstellung einer ortsaufgelösten BLS–Messung der Anregung
von Spinwellen–Kaustikstrahlen. Die Spinwelle wird durch eine Mikrowellenantenne im Eingangswellenleiter (Breite w = 400 µm) erzeugt. Am Übergang zur Propagationsfläche wird
eine Spinwelle mit dem benötigten weiten Wellenvektorspektrum angeregt und dadurch ein
Paar von Spinwellenstrahlen erzeugt. Die Strahlen propagieren ohne eine nennenswerte
Verbreiterung über mehr als 10 mm. Um die Dämpfung der Spinwellen zu kompensieren und
eine besseren Darstellung zu erhalten, wurde die gemessene Intensität in jeder Spalte der
Messung normiert. (H0 = 1860 Oe, ω = 2π · 7,132 GHz)
Für die Gesamtamplitude der Spinwelle am Ort r = (y, z) gilt dann
A(r) = ∑ Ak (k)eir·k
.
(5.5)
k
Dabei ist zu beachten, dass der Wellenvektor k = (ky , kz ) die Dispersionsrelation
(2.63) erfüllen muss und daher, bei gegebenem Magnetfeld H0 und gegebener Spinwellenfrequenz ω , nur eine der Komponenten frei gewählt werden kann. Es gilt
daher k = (ky , kz (ky )).
Die Amplitude im k–Raum Ak (k) = Ak (ky ) ergibt sich als Fourier–Transformation der Spinwellenamplitude am Ort der Kaustikanregung, hier also der Amplitude
am Ende des Wellenleiters. Diese ist sinusförmig, da sich senkrecht zum Wellenleiter eine stehende Welle ausbildet. Man erhält daher für einen Eingangswellenleiter
5.1 Grundlagen der Kaustikanregung
65
der Breite w
Ak (ky ) =
cos(ky w2 )
π2
w2
(5.6)
− ky2
und damit für die maximale Wellenvektorkomponente in y–Richtung
3π
ky,max =
.
w
Für die (komplexe) Gesamtamplitude ergibt sich also
A(y, z) = ∑
ky
cos(ky w2 )
π2
w2
− ky2
ei(yky +zkz (ky ))
,
(5.7)
(5.8)
wobei kz (ky ) durch die Dispersionsrelation gegeben ist. Dabei wird, wie bereits in
Kapitel 3.2 erwähnt wurde, aus den gemessenen Daten (genauer, aus den gemessenen Wellenlängen in den Eingangswellenleitern) eine effektive Magnetisierung MS
bestimmt und diese zur Berechnung von kz (ky ) verwendet.
Falls nötig kann die Dämpfung der Spinwellen in diesem Ansatz leicht durch das
Einführen eines komplexen Wellenvektors mit dem Imaginärteil
1
1
,
)
(5.9)
k′′ = γ · 2∆ H(
2vg,y 2vg,z
berücksichtigt werden. Dabei ist 2∆ H die FMR–Linienbreite (vgl. Kapitel 3.2) und
vg = (vg,y ,vg,z ) die Gruppengeschwindigkeit der Spinwelle.
Beim Vergleich der berechneten mit der gemessenen Kaustik ist zu beachten,
dass die Rechnung Amplituden liefert, während die BLS die Spinwellenintensität
misst. Die gemessenen Daten entsprechen daher dem Betragsquadrat von A(y, z)
BLSInt ∼ |A(y, z)|2
.
(5.10)
Das Äquivalent zu einer phasenaufgelösten BLS Messung erhält man aus Gl.(5.8)
durch Addition eines geeignet gewählten konstanten Referenzterms R und anschließender Bildung des Betragsquadrats
BLSPhase ∼ |A(y, z) + R|2
.
(5.11)
5.1.4 Theoretische Beschreibung des Profils eines Kaustikstrahls3
Wie bereits erwähnt, kann sich ein Kaustikstrahl ausbilden, wenn die Richtung der
Gruppengeschwindigkeit θ in einem gewissen Wellenvektorbereich nicht von der
3 Die
theoretische Beschreibung der Kaustikstrahlen wurden von V. S. Tiberkevich und A. N. Sla-
vin (Oakland Univesity, Rochester MI, USA) angeregt durch die vorliegenden experimentellen Ergebnisse durchgeführt und wird hier zusammengefasst wiedergegeben. Eine gemeinsamem Veröffentlichung ist in Vorbereitung [A12].
66
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
Richtung des Wellenvektors abhängig ist. Diese Bedingung kann in der Form
dθ
=0
dky
(5.12)
geschrieben werden. Beachtet man, dass θ als
θ = arctan
vg,y
dkz
= arctan
vg,z
dky
(5.13)
definiert ist (vgl. Kapitel 2.6.5), erhält man aus Gl. (5.12) die Bedingung
d2 kz
=0
dky2
.
(5.14)
Zur Berechnung des räumlichen Profils eines Kaustikstrahls ist es sinnvoll, die Dispersion zunächst als kz = kz (ky ,ω ) zu schreiben und anschließend um den Wellenvektor des Strahls kK in einer Taylor–Reihe zu entwickeln. Beachtet man Gl. (5.13)
und (5.14), erhält man
kz (ky ) ≈ kK,z − tan θK (ky − kK,y ) +
1 d3 kz
(ky − kK,y )3
6 dky3
.
(5.15)
Das Profil eines Kaustikstrahls, der am Ort r = 0 von einer punktförmigen Quelle angeregt wird, ergibt sich dann, wie schon bei der numerischen Beschreibung
(Gl. (5.5), aufgrund der punktförmigen Anregung ist hier Ak (k) = 1) durch eine inverse Fourier–Transformation
Z
1
η
−1/3
i(ky y+kz (ky )z)
2
a0 (r) =
e
dky = (ℓK ξ )
Ai
cos θK eikK ·r . (5.16)
2
1/3
2π
(ℓK ξ )
Im Gegensatz zu den bisherigen Rechnungen, wurde hier nicht die Damon–Eshbach
Dispersionsrelation benutzt, sondern zur Vereinfachung der Rechnung eine von Kalinikos und Slavin hergeleitete Näherung verwendet [104, 122]. Ai(x) ist die Airy–
Funktion (siehe zum Beispiel [114]), ξ = z cos θK + y sin θK die Koordinate entlang
und η = −z sin θK + y cos θK die Koordinate senkrecht zum Kaustikstrahl. Weiter
wird die charakteristische Längenskala des Kaustikstrahls
ℓK =
1 d3 kz
2 dky3
!1/2
cos2 θK
(5.17)
eingeführt. Anzumerken ist, dass aufgrund der verwendeten Taylor–Entwicklung
Gl. (5.16) nur in der räumlichen Umgebung des Strahls gilt.
5.2 Kontrolle der Kaustikanregung durch externe Parameter
67
Aus Gl. (5.16) lässt sich das Profil eines “realen” Kaustikstrahls, der von einer
Antenne der Breite w mit der Amplitudenverteilung s(y) angeregt wurde, als
a(r) =
Z w
0
a0 (r − yey )s(y)dy
(5.18)
berechnen. Da Gl. (5.16) einen oszillierenden Term der Form eikK ·r enthält, wird
das Integral in Gl. (5.18) klein, wenn w > 2π/kK ist. Wie bereits in den letzten
Kapiteln angesprochen, muss daher die Antenne kleiner als die Wellenlänge des
Kaustikstrahls sein, damit eine nennenswerte Anregung zustandekommt.
Wie man anhand des Arguments der Airy–Funktion in Gl. (5.16) erkennt, wird
die Veränderung der transversale Ausdehnung mit der Propagationsdistanz ξ durch
den Ausdruck (ℓ2K ξ )1/3 bestimmt. Dabei muss allerdings beachtet werden, dass
Gl. (5.16) nur für die Anregung mit einer punktförmigen Antenne gilt. Im Fall einer
realen Antenne wird man erst dann eine Verbreiterung beobachten, wenn die “theoretische Breite” (ℓ2K ξ )1/3 größer als die anfänglich von der Antenne vorgegebene
Breite w ist. Damit kann die Distanz, über die eine stabile Propagation möglich ist,
mit
2
w
ξ∗ = w
(5.19)
ℓK
abgeschätzt werden. Führt man die beschriebenen Rechnungen für die hier verwendeten experimentellen Parameter (H0 = 1840 Oe, w = 400 µm) durch, so ergibt sich
eine charakteristische Längenskala von ℓK ≈ 24,5 µm und damit eine stabile Propagationsdistanz von ξ∗ ≈ 10,7 cm.
5.2 Kontrolle der Kaustikanregung durch externe Parameter
Zum besseren Verständnis der Kaustikanregung wurden Messungen bei verschiedenen angelegten Feldern H0 und mit verschieden breiten Eingangswellenleitern
durchgeführt. Abbildung 5.4 zeigt Beispiele für BLS–Messungen (dargestellt in der
oberen Reihe der jeweiligen Abbildung) und die für die entsprechenden Parameter
durchgeführten numerischen Rechnungen (untere Reihe).
Wie deutlich zu erkennen ist, bilden sich für das niedrigste Feld (H0 = 1840 Oe)
bei beiden Eingangswellenleitern scharf abgegrenzte Kaustikstrahlen. Wie zu erwarten war, wird ihre laterale Ausdehnung durch die Breite des Wellenleiters bestimmt.
Bei höheren Feldern ergeben sich allerdings ausgeprägte Unterschiede für die beiden
Eingangswellenleiter. Für den breiteren Wellenleiter (w = 750 µm, Abb. 5.4(b)) beobachtet man eine deutliche Verkleinerung des Propagationswinkels θ und eine Zunahme der Spinwellenintensität zwischen den Kaustikstrahlen, die schließlich zum
68
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
BLS
Rechnung
H0 = 1840 Oe
H0 = 1860 Oe
H0 = 1880 Oe
(a) w = 400 µm
BLS
Rechnung
H0 = 1840 Oe
H0 = 1860 Oe
H0 = 1880 Oe
(b) w = 750 µm
Abbildung 5.4: Logarithmische Falschfarbendarstellung der Kaustikanregung für verschiedene Eingangswellenleiter und Felder. Man erkennt eine gute qualitative Übereinstimmung
zwischen BLS–Messungen (jeweils obere Reihe) und numerischen Rechnungen (jeweils untere Reihe). (ω = 2π · 7,132 GHz)
5.2 Kontrolle der Kaustikanregung durch externe Parameter
69
Verschwinden der Strahlen führt. Bei den Kaustikstrahlen, die mit Hilfe des schmaleren Wellenleiters (w = 400 µm, Abb. 5.4(a)) angeregt wurden, zeigen sich diese
Effekte nur in abgeschwächter Form und erst bei höheren Feldern. Die durchgeführten Rechnungen zeigen eine gute qualitative Übereinstimmung mit den Messungen
und bestätigen somit das beobachtete Verhalten.
Zur weiteren Überprüfung der Abhängigkeit der Kaustikanregung von angelegtem Feld und Eingangswellenleiter wurden Rechnungen für Felder im Bereich von
H0 = 1840 – 1900 Oe und Wellenleiter der Breite w = 100 – 1000 µm durchgeführt.
Abbildung 5.5 zeigt eine Zusammenfassung dieser Rechnungen. In Abb. 5.5(a) ist
der Propagationswinkel θ als Funktion von H0 und w dargestellt; Abb. 5.5(b) zeigt
den gemittelten Intensitätskontrast der Kaustikstrahlen. Dieser wurde gemäß
Kontrast =
IStrahl − IMitte
IStrahl + IMitte
(5.20)
berechnet, wobei IStrahl die Intensität des Kaustikstrahls und IMitte die Intensität in der
Mitte zwischen den beiden Strahlen, dass heißt bei y = 0 mm, ist. Die Mittelwertbildung erfolgt über alle Punkte entlang der z–Achse. Zur Definition des Kaustikstrahls
in den berechneten Daten wird für jeden Punkt der z–Achse die y–Koordinate des Intensitätsmaximus bestimmt.
Wie Abb. 5.5 zeigt, bestätigt die Rechnung die experimentell beobachteten Abhängigkeiten. Winkel wie auch Kontrast der Kaustikstrahlen nehmen für steigendes
Feld und zunehmende Breite des Wellenleiters ab.
Dieses Verhalten kann nicht alleine durch die θ (φ )–Abhängigkeit verstanden
werden, da diese nicht durch den Anregungsprozess beeinflusst wird und daher von
w unabhängig ist. Daher muss zusätzlich das Anregungsspektrum der Wellenleiterantenne Ak (φ ) berücksichtigt werden. Ak (φ ) kann dabei leicht mit Hilfe der Dispersionsrelation aus Gl. (5.6) berechnet werden.
Abbildung 5.6 zeigt θ (φ ) und Ak (φ ) für verschiedene Felder und Eingangswellenleiter. Vergleicht man beide Kurven, so erkennt man sofort die Ursache für das
beschriebene Verhalten. Ist das Spektrum Ak (φ ) weit genug ausgedehnt und beinhaltet den “Kaustikbereich”, das heißt die Plateaus in der θ (φ )–Kurve, können sich
Kaustikstrahlen ausbilden. Wird das angelegte Feld erhöht, ändern sich beide Kurven. Das Spektrum Ak (φ ) wird schmaler, da der Trägerwellenvektor kz durch die
Verschiebung der Dispersionsrelation größer wird (siehe Kapitel 2.6.4 und Gl. (5.2)).
Gleichzeitig wird das Plateau der θ (φ )–Abhängigkeit schmaler, so dass der Anteil
des Spektrums der zur Anregung des Kaustikstrahls beiträgt geringer wird. Weiter beobachtet man, dass der Betrag des Winkels θK sinkt. Wird der Eingangswellenleiter breiter, wird der maximale Wellenvektor in y–Richtung ky,max kleiner
(vgl. Gl. (5.7)) und damit das Anregungsspektrum schmaler.
70
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
θ [◦ ]
Kaustikanregung
H0 [Oe]
w [µm]
(a) Propagationswinkel θ
Kontrast [%]
Kaustikanregung
H0 [Oe]
w [µm]
(b) Kontrast
Abbildung 5.5: Propagationswinkel (a) und Kontrast (b) der numerisch berechneten Kaustikstrahlen als Funktion des Magnetfelds H0 und der Breite des Eingangswellenleiters w.
(ω = 2π · 7,132 GHz)
5.3 Kaustik–“Feinstruktur”
71
40
θ [◦ ]
20
0
-20
-40
Ak [a.u.]
1,0
0,5
0,0
-40
-20
0
20
40
φ [◦ ]
Abbildung 5.6: Propagationswinkel θ (φ ) (oben) und Anregungsspektrum Ak (φ ) (unten) für
verschiedene Felder H0 und Eingangswellenleiterbreiten w. (H0 = 1840 Oe (rot) beziehungsweise 1880 Oe (blau), w = 400 µm (durchgezogene Linie) beziehungsweise w = 750 µm (gepunktete Linie), ω = 2π · 7.132 GHz)
Zusammengenommen führen diese beiden Effekte wie beobachtet also zu einer
Verringerung des Winkels θK und einer Verringerung des Kontrastes bei steigenden
Magnetfeldern und breiter werdenden Eingangswellenleitern.
5.3 Kaustik–“Feinstruktur”
Betrachtet man die numerisch berechnete Kaustikintensität in Abb. 5.4 genauer, so
erkennt man für das kleinste Feld zwischen den beiden Kaustikstrahlen eine “Feinstruktur” in Form von dünnen Linien, parallel zu den Strahlen. Diese Struktur ist
in den experimentellen Daten nicht sichtbar. Wie man anhand von Abb. 5.7 sieht,
ist allerdings das Signal–zu–Rausch–Verhältnis zwischen den beiden Strahlen in der
Messung nicht ausreichend, um diese Struktur zu beobachten. Trotzdem kann, insbesondere auf der linken Seite der Messung, eine leichte Erhöhung der gemessenen
Intensität, in dem Bereich, in dem die Oszillationen theoretisch erwartet werden, beobachtet werden. Dies kann als Hinweis auf die Existenz der Feinstruktur gedeutet
werden.
72
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
Messung
Numerische Rechnung
Analytische Rechnung
Amplitude [a.u.]
1,0
0,5
0,0
-3
-2
-1
0
1
2
3
y [mm]
Abbildung 5.7: Profil der angeregten Spinwellen–Kaustikstrahlen im Abstand von 2,5 mm
vom Ort der Anregung. Sowohl die numerische (rot), wie auch die analytische Rechnung
(grün) zeigen eine Feinstruktur in Form von Oszillationen zwischen den beiden Strahlen.
Wie zu erkennen ist, ist das Signal–zu–Rausch–Verhältnis der Messung nicht ausreichend,
um diese Struktur im Experiment beobachten zu können. (H0 = 1840 Oe, w = 400 µm,
ω = 2π · 7,132 GHz)
Vergleicht man die analytische Rechnung (Gl. (5.16)) mit den numerischen Daten, erkennt man allerdings eine qualitative Übereinstimmung des Verhaltens, so
dass sichergestellt ist, dass diese Feinstruktur eine physikalische Ursache hat und
kein Artefakt der Numerik ist.
In einem stark vereinfachten Modell (vorgeschlagen von Tiberkevich und Slavin)
kann die Entstehung und die Feld- und Antennenbreitenabhängigkeit der Feinstruktur erklärt werden.
Für den Bereich oberhalb des Winkels θK existieren keine Spinwellen, daher
kann oberhalb von θK keinerlei Struktur beobachtet werden. Für θ < θK existieren
dagegen zwei Wellen, die mit diesem Winkel propagieren, eine mit einem Wellenvektorwinkel oberhalb und eine mit einem Wellenvektorwinkel unterhalb des Kaustikbereichs (siehe Abb. 5.1). Aufgrund der verschiedenen Wellenvektoren kommt es
daher abhängig von θ zu konstruktiver oder destruktiver Interferenz, so dass es für
θ < θK zur Ausbildung der beobachteten Feinstruktur kommt.
5.4 Phasenstruktur von Spinwellen–Kaustikstrahlen
73
BLS
Rechnung
H0 = 1840 Oe
H0 = 1860 Oe
H0 = 1880 Oe
Abbildung 5.8: Phasenstruktur der Spinwellen–Kaustikstrahlen für verschiedene Magnetfelder H0 . BLS–Messungen (obere Reihe) und numerische Rechnungen (untere Reihe) zeigen
eine gute qualitative Übereinstimmung. (H0 = 1840 Oe, w = 750 µm, ω = 2π · 7,132 GHz).
Wird das Anregungsspektrum durch Änderung von H0 oder w schmaler, werden
weniger oder gar keine Spinwellen oberhalb des Kaustikbereichs angeregt und die
Feinstruktur verschwindet, wie in den numerischen Rechnungen beobachtet.
5.4 Phasenstruktur von Spinwellen–Kaustikstrahlen
Die Phasenstruktur der Kaustikstrahlen konnte mit Hilfe der phasenaufgelösten BLS
untersucht werden. Die Messungen (und die entsprechenden numerischen Rechnungen) sind in Abb. 5.8 dargestellt. Auch hier erkennt man eine gute qualitative
Übereinstimmung zwischen Rechnung und Messungen. Die prinzipielle Phasenstruktur wird hauptsächlich durch die Dispersion und die θ (φ )–Abhängigkeit der
Spinwelle bestimmt und hängt damit nur wenig vom gewählten Wellenleiter ab.
Da für den breiteren Wellenleiter (w = 750 µm) breitere Kaustikstrahlen ausgebildet werden, ist die Phasenstruktur in diesem Fall besser sichtbar, daher sind nur die
Messungen für diesen Wellenleiter abgebildet. Wie deutlich zu erkennen ist, ist die
Wellenlänge innerhalb des Wellenleiters etwa gleich der Wellenlänge in der Mitte
zwischen den Strahlen, da beide Fälle näherungsweise als ebene Welle beschrieben werden können. Innerhalb der Kaustikstrahlen wird die Wellenlänge deutlich
kürzer. Wie aufgrund der θ (φ )–Abhängigkeit zu erwarten war, liegen die Phasen-
74
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
H0
(a) Geometrische Reflexion
H0
(b) Nicht–geometrische Reflexion
Abbildung 5.9: “Reflexion” von Spinwellen–Kaustikstrahlen. (w = 400 µm, H0 = 1840 Oe,
ω = 2π · 7,132 GHz)
fronten nicht senkrecht zur Ausbreitungsrichtung, da Gruppengeschwindigkeit und
Wellenvektor nicht parallel sind.
Weiter kann man deutlich erkennen, dass die Wellenlänge innerhalb der Kaustikstrahlen vergleichbar mit der Breite des Strahls ist. Da sich derart schmale Strahlen normalerweise während der Propagation sehr stark verbreitern sollten, beweist
das klar das Vorhandensein eines stabilisierenden Einflusses der induzierte Anisotropie.
Bei der Betrachtung der Phasenstruktur darf nicht vergessen werden, dass der
Kaustikstrahl aus der Interferenz vieler Spinwellen mit verschieden gerichteten Wellenvektoren entsteht. Wellenlänge und Wellenvektor des Kaustikstrahls entsprechen
daher nicht den Werten einer bestimmten Spinwelle, sondern sind nur innerhalb des
so gebildeten Strahls definiert.
5.5 Reflexion und Streuung von Spinwellen–Kaustikstrahlen
Während bisher nur die freie Propagation von Spinwellen–Kaustikstrahlen behandelt
wurde, soll in diesem Kapitel die Reflexion an den Begrenzungen der Probe und die
Streuung an einem Defekt betrachtet werden.
Abbildung 5.9(a) zeigt die geometrische Reflexion eines Spinwellen–Kaustikstrahls am Rand der Probe. Dabei sind Einfalls- und Ausfallswinkel gleich. Diese
Reflexion kann nach dem Huygensschen Prinzip durch die Streuung der einfallenden
Spinwelle an der Kante der Probe beschrieben werden. Die Kante wirkt demnach als
sekundäre Antenne, die einen neuen Kaustikstrahl anregt. Die Ausbreitungsrichtung
dieses “reflektierten” Strahls wird daher nicht von der Ausrichtung der Kante son-
5.5 Reflexion und Streuung von Spinwellen–Kaustikstrahlen
H0
Defekt
Abbildung 5.10: Streuung eines Spinwellen–Kaustikstrahls an einem mechanischen Defekt.
(w = 500 µm, H0 = 1840 Oe, ω = 2π · 7,132 GHz)
dern über θ (φ ) von der Richtung des angelegten Felds bestimmt. Liegt dieses wie
in der in Abb. 5.9(a) gezeigten Messung parallel zur Kante, kann eine geometrische
Reflexion beobachtet werden. Im Gegensatz dazu führt eine andere Ausrichtung des
Felds zu nicht–geometrischer Reflexion. Bei dieser sind Ein- und Ausfallswinkel
verschieden. Abbildung 5.9(b) zeigt eine Messung der nicht–geometrischen Reflexion eines Kaustikstrahls. In beiden Fällen (geometrische und nicht–geometrische
Reflexion) ist dabei die Ausbreitungsrichtung in Bezug auf die Richtung von H0 für
den einfallenden und für den “reflektierten” Strahl gleich.
Vergleicht man Abb. 5.9(a) und (b), so erkennt man neben der nicht–geometrischen Reflexion weitere Unterschiede. Da die Symmetrieachse der Anregung
durch die Richtung des Felds gegeben ist, propagieren die beiden Strahlen in (b)
in Bezug auf die Probengeometrie unter verschiedenen Winkeln. Da gleichzeitig
das Anregungsspektrum Ak (φ ) entlang der φ –Achse verschoben wird (da φ = 0◦
durch die Richtung von H0 und nicht durch die Achse des Wellenleiters definiert
ist) werden beide Kaustikstrahlen außerdem mit verschiedener Intensität angeregt.
Die Wahl einer geeigneten Ausrichtung des Felds erlaubt daher die Kontrolle von
Richtung (bezogen auf die Probe) und relativer Intensität der Spinwellenstrahlen.
Abbildung 5.10 zeigt ein weiteres Beispiel für die Streuung eines Spinwellen–
Kaustikstrahls. Dargestellt ist die Streuung des Strahls an einem Defekt im YIG
(markiert durch einen Pfeil). Dabei wurde das magnetische Feld unter einem Winkel
von 30◦ gegenüber dem Eingangswellenleiter angelegt, so dass die Kaustikstrahlen
stark unsymmetrisch angeregt werden. Durch die Streuung entstehen neue Strahlen,
75
76
Anregung und Untersuchung von Spinwellen–Kaustikstrahlen
die alle unter demselben Winkel θ in Bezug auf das angelegte Feld propagieren. Wie
man anhand des Interferenzmusters im einfallenden Strahl erkennt, werden dabei
Kaustikstrahlen erzeugt, die in alle vier möglichen Richtungen propagieren. Ähnlich
wie in [104] wirkt der Defekt also als Antenne, die weitere Kaustikstrahlen anregt.
Kapitel 6
Spinwellenlogikgatter
Während magnetische Effekte schon lange für die Datenspeicherung eingesetzt werden (Festplatten, MRAM), gibt es erst seit wenigen Jahren Ansätze zur Realisierung von magnetischen Logikgattern. Vorgeschlagen wurden zum Beispiel AND–
und NOT–Gatter, die auf der Manipulation von Domänenwänden in Permalloy–
Nanodrähten basieren [123, 124], oder ein aus Nanomagneten aufgebauter zellulärer
Automat (Magnetic Quantum–Dot Cellular Automata MQCA) [125, 126]. Weitere Konzepte basieren auf dem Magnetowiderstand einzelner magnetischer Elemente [127–131]. Diese haben gegenüber konventioneller (CMOS–)Logik den Vorteil, dass die durchgeführte logische Operation während der Laufzeit bestimmt (und
geändert) werden kann. Ein weiterer Vorteil aller bisher genannten Vorschläge ist,
dass das Ausgangssignal im Gatter auch nach dem Ende der Operation erhalten
bleibt.
Alternativ wurden verschiedene Konzepte vorgeschlagen, die die Manipulation von Spinwellen zur Realisierung logischer Operationen verwenden [A1, A2, 7–
11]. Alle diese Ansätze verwenden verschiedene Arten von Spinwelleninterferometern, bei denen die Phase der interferierenden Spinwelle gezielt manipuliert werden
kann. Die Phasenänderung erfolgt dabei durch Propagation der Spinwellen durch
Domänenwände [7], Änderung der Polarität des Anregungspulses [8] oder lokale
Änderungen des magnetischen Felds [A1, A2, 9–11]. Wie von Khitun et al. [8, 9]
vorgeschlagen, können Spinwellen auch zur Datenübermittlung zwischen den Logikgattern verwendet werden, so dass komplexe Operationen in einer reinen Spinwellenarchitektur durchgeführt werden können.
Das Prinzip der hier realisierten Spinwellenlogik basiert auf einer Idee von Mikhail P. Kostylev [A1, A2]. Grundlage ist wie auch in [7] ein Spinwellen–Mach–
Zehnder–Interferometer. Zur Manipulation der Spinwellen in dessen Armen wird
bei dem hier verwendeten Konzept allerdings die lokale Änderung des magnetischen
Felds H0 durch fließende Ströme verwendet. Damit kann nicht nur die Phase, son-
78
Spinwellenlogikgatter
dern auch die Amplitude der propagierenden Spinwellen beeinflusst werden (siehe
Kapitel 6.1). Dies ermöglicht die Realisierung von XNOR–, NAND– und NOT–
Gattern (Kapitel 6.2).1 Im Rahmen dieser Arbeit wurde das ursprüngliche Konzept
des Interferometers (bestehend aus zwei Spinwellenwellenleitern) zu einem Interferometer mit einem Wellenleiter (Kapitel 6.3) weiterentwickelt, das ohne zusätzliche Mikrowellenleistungsteiler auskommt.
6.1 Prinzip des Spinwelleninterferometers
Die einfachste Realisierung eines Spinwelleninterferometers auf Basis von YIG–
Wellenleitern ist in Abb. 6.1 dargestellt. Ein Mikrowellensignal wird mit Hilfe eines Leistungsteilers geteilt und zur Anregung von (Backward–Volume–)Spinwellen
in zwei identischen Spinwellenwellenleitern (Breite 1,5 mm, Dicke 6 µm) verwendet. Der anfängliche Phasenunterschied zwischen den beiden Spinwellen kann mit
Hilfe eines Mikrowellen–Phasenschiebers eingestellt werden. Die Mikrowellensignale, die am Ende der Wellenleiter registriert werden, werden in einem weiteren
Leistungsteiler miteinander überlagert; das resultierende Interferenzsignal kann mit
einem Oszilloskop dargestellt werden.
Das Oersted–Feld eines Stromes, der durch eine Drahtschleife (Durchmesser des
Drahtes 500 µm) beziehungsweise durch einen dünnen Draht (Durchmesser
100 µm) in direktem Kontakt mit dem Wellenleiter fließt, ermöglicht eine kontrollierte, lokale Änderung des magnetischen Feldes in jedem der beiden Wellenleiter.
Im ersten Fall erhält man eine ausgedehnte, schwache Änderung von H0 , die zu
einer Phasenverschiebung der jeweiligen Spinwelle führt (siehe Kapitel 6.1.1). Im
Gegensatz dazu liefert der dünne Draht eine starke, wenig ausgedehnte Änderung
des Felds, die die Amplitude der Spinwelle beeinflusst (siehe Kapitel 6.1.2). Beide Effekte führen zu einer sichtbaren Änderung des gemessenen Interferenzbilds.
Um auszuschließen, dass es sich dabei um thermische Effekte handelt, wurden in
allen hier vorgestellten Experimenten gepulste Ströme und Spinwellen mit geringer Wiederholrate (TR = 10 ms bei Mikrowellenmessungen, TR = 25 µs bei BLS–
Messungen) verwendet.
Die Verwendung von YIG–Wellenleitern in den Interferometerarmen erlaubt aufgrund der bereits erwähnten geringen Dämpfung dieses Materials den Aufbau eines makroskopischen Prototyps. Da sich die verwendeten physikalischen Prinzipien
beim Übergang zu geringeren Größen nicht ändern, können die im Folgenden vorgestellten Logikgatter auch mit Mikrometerstrukturen, zum Beispiel auf Basis von
Permalloy, realisiert werden. Diese Verkleinerung kann auch durch den Übergang
1 In
[A1] wurden bereits vorläufige Ergebnisse der Gatter vorgestellt. Diese konnten hier deutlich
verbessert werden.
6.1 Prinzip des Spinwelleninterferometers
79
I2
H0
∆ϕ
I1
Abbildung 6.1: Aufbau eines Spinwellen–Mach–Zehnder–Interferometers.
zu austauschdominierten Spinwellen (siehe Kapitel 2.5) erreicht werden wie in [10]
theoretisch gezeigt wurde. Da in diesem Fall allerdings eine andere Dispersionsrelation zugrundeliegt, sind die in den nächsten Kapiteln beschriebenen Ergebnisse nicht
ohne weiteres übertragbar.
Ein alternativer Aufbau für ein Spinwelleninterferometer wurde kürzlich in [11]
vorgeschlagen. Auch bei dieser Struktur kann das externe Feld durch das Fließen
eines Stroms geändert werden. Im Gegensatz zu dem hier verwendeten Interferometer fließt der Strom allerdings zwischen den beiden Armen des Interferometers
senkrecht zur Struktur. Dadurch wird das Feld in einem der beiden Arme vergrößert
und in dem anderen reduziert. Die Autoren konnten zeigen, dass die Reihen- beziehungsweise Parallelschaltung von zwei Interferometern dieser Art als Not–OR–
beziehungsweise Not–AND–Gatter verwendet werden kann.
6.1.1 Kontrolle der Phase von Spinwellen durch Ströme
Wie in Kapitel 2.6.4 gezeigt wurde, führt eine Änderung des magnetischen Felds,
zum Beispiel durch das Oersted–Feld eines Stroms, zu einer Verschiebung der Dispersionskurve entlang der Frequenzachse. Da die Frequenz der Spinwelle nicht
geändert wird, folgt daraus eine lokale Änderung des Wellenvektors k(z), für die im
Fall einer nicht zu starken Verschiebung
∆ k(z) = (k(z) − k0) ∼ ∆ H(z) ∼ I
(6.1)
80
Spinwellenlogikgatter
l
∆ϕ ∼ ∆z
Arm 1
Arm 2
∆ ϕ [π]
Amplitude [a.u.]
2,0
1,5
1,0
0,5
0,0
0
200
z [a.u.]
400
600
800
1000
I [mA]
(a) Ursache
(b) Messung
Abbildung 6.2: (a) Ursache der Phasenverschiebung. Propagiert eine Spinwelle (durchgezogene Linie) durch einen Bereich mit geändertem Feld (grau hinterlegt, ∆ H(z) < 0 zur Vereinfachung als stufenförmig angenommen), ändert sich in diesem Bereich ihr Wellenvektor und
damit die Wellenlänge (λ (z) > λ0 ). Dies führt zu einer Phasenverschiebung ∆ ϕ gegenüber
der Welle, die nicht durch das geänderte Feld beeinflusst wird (gepunktete Linie) [132].
(b) Messung der Phasenverschiebung in beiden Armen des hier verwendeten Interferometers
als Funktion des Stromes durch die Drahtschleife. (H0 = 1850 Oe, ω = 2π · 7,132 GHz)
gilt [A2].2 Dabei ist ∆ H(z) das Feldprofil entlang der Propagationsachse z, das durch
den Strom I erzeugt wird, und k0 der Wellenvektor außerhalb der Feldänderung. Ist
∆ H(z) im Bereich 0 ≤ z ≤ l lokalisiert, ergibt sich daraus für die Phasenverschiebung
∆ ϕ gegenüber einer Welle mit unverändertem Wellenvektor
∆ϕ =
Zl
∆ k(z)dz .
(6.2)
0
Damit gilt näherungsweise ∆ ϕ ∼ Il. Abbildung 6.2(a) veranschaulicht die Ursache
dieser Phasenverschiebung.
Für die Anwendung dieses Effekts in einem Spinwellenphasenschieber ist es notwendig, dass die Amplitude der Spinwelle durch ∆ H(z) nicht (oder nur wenig) beeinflusst wird. Da eine starke Änderung des Felds zu einer ausgeprägten Reflexion
der Spinwelle führt (siehe zum Beispiel [A6, 106]), darf ∆ H(z) nicht zu groß sein.
Um trotzdem eine nennenswerte Phasenverschiebung zu erreichen, kann die Ausdehnung l von ∆ H(z) vergrößert werden. Wie bereits erwähnt, erfüllt das Oersted–Feld
einer stromdurchflossenen Drahtschleife diese Voraussetzungen.
2 Dabei ist
zu beachten, dass bei den hier verwendeten Backward–Volume–Wellen der Wellenvek-
tor negativ ist. Ist ∆ H(z) < 0, folgt daraus zwar |k(z)| < |k0 | aber trotzdem ∆ k(z) > 0.
Amplitude [a.u.]
6.1 Prinzip des Spinwelleninterferometers
350
81
I = 1200 mA
I = 0 mA
400
450
Zeit [ns]
500
350
400
450
500
450
500
Zeit [ns]
Amplitude [a.u.]
(a) Arm 1
350
I = 0 mA
400
I = 1200 mA
450
Zeit [ns]
500
350
400
Zeit [ns]
(b) Arm 2
Abbildung 6.3: Kontrolle der Spinwellenamplitude durch Spinwellentunneln. Abhängig vom
Strom durch den dünnen Draht kann der Spinwellenpuls fast vollständig unterdrückt werden.
(H0 = 1850 Oe, ω = 2π · 7,132 GHz)
Abbildung 6.2(b) zeigt die gemessene Phasenverschiebung für beide Arme des
verwendeten Spinwelleninterferometers als Funktion des Stromes durch die Drahtschleife. Die aus Gl. (6.2) folgende lineare Beziehung zwischen I und ∆ ϕ ist deutlich zu erkennen. Weiter zeigen die Messungen, dass eine Phasenverschiebung von
π leicht zu erreichen ist und der dazu notwendige Strom Iπ für beide Arme praktisch
gleich ist.
6.1.2 Kontrolle der Amplitude von Spinwellen durch Ströme
Zur Kontrolle der Spinwellenamplitude mit Hilfe von Strömen kann der in [106] beschriebene Effekt des Spinwellentunnelns verwendet werden. Dabei wird durch eine
starke lokale Änderung des magnetischen Felds (zum Beispiel durch einen dünnen
Draht in direktem Kontakt mit dem Wellenleiter) die Dispersionskurve soweit zu
kleineren Frequenzen verschoben, dass die Frequenz der Spinwelle außerhalb des
für Backward–Volume–Wellen erlaubten Frequenzbereichs liegt. Dadurch entsteht
ein “verbotener Bereich”, den die Spinwelle durchtunneln muss.
82
Spinwellenlogikgatter
Eine Erhöhung der Stromstärke führt zu einer Verbreiterung dieses Bereichs und
damit zu einer reduzierten Transmission. Ist die lokale Feldänderung (das heißt der
Strom) stark genug, wird die Propagation der Spinwelle fast vollständig verhindert.
Der beschriebene Aufbau kann damit als Spinwellenschalter verwendet werden. Abbildung 6.3 demonstriert dies für beide Arme des hier verwendeten Interferometers.
Alternativ kann auch, wie in [A6, 133] gezeigt, eine lokale Vergrößerung des
Felds verwendet werden, um die Spinwellenamplitude zu kontrollieren. In diesem
Fall ist allerdings die Abhängigkeit der Transmission von ∆ H nichtmonoton, so dass
leichte Unterschiede zwischen den beiden Armen, wie zum Beispiel geringfügig verschiedene Abstände zwischen YIG–Film und Draht, zu deutlich unterschiedlichen
Spinwellenamplituden führen können. Insbesondere in Hinblick auf eine potentielle
Anwendung erscheint daher die lokale Verminderung des Felds zur Kontrolle der
Amplitude sinnvoller.
6.2 Realisierung von XNOR–, NAND– und NOT–
Spinwellenlogikgattern
Nachdem die einzelnen Elemente des Spinwelleninterferometers (Abb. 6.1) vorgestellt wurden, wird im Folgenden gezeigt, wie damit XNOR–, NAND– und NOT–
Logikgatter realisiert werden können. Tabelle 6.1 zeigt das Verhalten dieser logischen Operationen. Dem NAND–Gatter kommt dabei besondere Bedeutung zu, da
durch die geeignete Kombination mehrerer NANDs alle weiteren logischen Operationen konstruiert werden können.
6.2.1 XNOR–Gatter
Zum Aufbau eines XNOR–Gatters werden die beiden Drahtschleifen (Phasenschieber) des Interferometers verwendet. Ein zusätzlicher (Mikrowellen–)Phasenschieber
in einem der beiden Arme dient zum Ausgleichen unterschiedlich langer Kabel in
den Zu- und Ableitungen des Interferometers. Er muss so eingestellt werden, dass
ohne einen anliegenden Strom die Spinwellensignale beider Arme konstruktiv interferieren.
Die Ströme I1 und I2 dienen als logische Eingänge, wobei I = 0 A der logischen
Null und ein Strom von I = Iπ der logischen Eins entspricht. Das Ausgangsignal des
Gatters wird durch das Interferenzsignal repräsentiert. Dabei entspricht konstruktive Interferenz (= hohe Intensität) der logischen Eins und destruktive Interferenz
(= niedrige Intensität) der logischen Null. Die Mikrowellenpulse am Eingang des
Interferometers entsprechen den Taktpulsen.
6.2 Realisierung von XNOR–, NAND– und NOT–Spinwellenlogikgattern
Eingänge
Ausgang
Eingänge
Ausgang
A (I1 ) B (I2 )
A&B
A
(I1 )
B
(I2 )
A=B
0
(0)
0
(0)
1
0
(0)
0
(0)
1
0
(0)
1
(Iπ )
0
0
(0)
1
(Is )
1
1
(Iπ )
0
(0)
0
1
(Is )
0
(0)
1
1
(Iπ )
1
(Iπ )
1
1
(Is )
1
(Is )
0
(a) XNOR
(b) NAND
Eingang
Ausgang
A
(I1 )
A
0
(0)
1
1
(Is , Iπ )
0
(c) NOT
Tabelle 6.1: Wahrheitstabellen der realisierten Logik–Gatter.
Liegt an beiden Eingängen dasselbe logische Signal (I1 = I2 ) an, sind die Spinwellen in beiden Armen in Phase. Man erhält konstruktive Interferenz und damit eine logische Eins am Ausgang. Unterscheiden sich die logischen Signale, ergibt sich
ein Phasenunterschied von π zwischen beiden Armen. Dies führt zu destruktiver
Interferenz (logische Null). Dieses Verhalten ist in Tabelle 6.1(a) zusammengefasst;
es entspricht einem eXclusive–Not–OR– oder XNOR–Gatter, auch Äquivalenz genannt.
Zur experimentellen Realisierung dieses Gatters wurde, wie bereits beschrieben,
ein Spinwelleninterferometer aus YIG–Wellenleitern verwendet. Die logischen Eingangssignale wurden durch Strompulse der Länge 990 ns erzeugt. Die Länge dieser
Pulse kann, falls gewünscht, bis auf die Länge der Spinwellenpulse reduziert werden,
in diesem Fall wird allerdings ein höherer Strom benötigt, um die Phasenverschiebung von π zu erreichen.
In Abb. 6.4 sind die gemessenen Ausgangssignale für die vier möglichen Kombinationen der Eingangssignale des XNOR–Gatters gezeigt. Die Unterschiede zwischen konstruktiver und destruktiver Interferenz (dass heißt logische Null und Eins)
sind deutlich sichtbar; der vorgeschlagene Aufbau kann damit als Logikgatter verwendet werden.
83
84
Spinwellenlogikgatter
=
1
1
0
=
0
1
0
=
0
1
1
=
1
Amplitude [a.u.]
0
0
400
500
400
500
400
500
400
500
Zeit [ns]
Abbildung 6.4: Ausgangssignale eines Spinwellen XNOR–Gatters für die im jeweiligen
Diagramm angegebenen Eingangssignale. (H0 = 1850 Oe, ω = 2π · 7,132 GHz, Pulslänge
τ = 20 ns)
6.2.2 NAND–Gatter
Der prinzipielle Aufbau eines NAND–Gatters entspricht dem des XNOR–Gatters,
mit dem Unterschied, dass hier der Strom durch die dünnen Drähte (Spinwellenschalter) als logisches Eingangssignal verwendet wird und damit die Amplitude der
Spinwelle beeinflusst wird. Kein Strom entspricht dabei wieder der logischen Null.
Als logische Eins wird der Strom Is verwendet, der notwendig ist, um die Spinwelle
vollständig zu unterdrücken. Im Gegensatz zum XNOR–Gatter, bei dem die Signale beider Arme ohne anliegenden Strom in Phase sind, ist hier ein voreingestellter
Phasenunterschied von 2π/3 zwischen den beiden Armen nötig. Bei diesem Phasenunterschied ist die Intensität des Interferenzsignals gleich der Intensität der beiden
einzelnen Signale.
Liegt an nur einem oder keinem Eingang eine logische Eins an, ändert sich aufgrund der eingestellten Phasenverschiebung das Ausgangssignal nicht, daher erhält
man in diesen Fällen eine logische Eins am Ausgang. Sind beide logischen Eingänge
Eins (das heißt durch beide Drähte fließt der Strom Is ) wird das Ausgangssignal
vollständig unterdrückt; es ergibt sich eine logische Null (siehe Tabelle 6.1(b)). Man
erhält also ein Not–AND– oder NAND–Gatter.
Abbildung 6.5 zeigt die gemessenen Ausgangssignale des NAND–Gatters. Auch
hier ist das beschriebene Verhalten klar zu erkennen.
6.2 Realisierung von XNOR–, NAND– und NOT–Spinwellenlogikgattern
&
1
1
0
&
0
1
1
&
1
1
1
&
0
Amplitude [a.u.]
0
0
85
400
500
400
500
400
500
400
500
Zeit [ns]
Abbildung 6.5: Ausgangssignale eines Spinwellen NAND–Gatters für die im jeweiligen
Diagramm angegebenen Eingangssignale. (H0 = 1850 Oe, ω = 2π · 7,132 GHz, Pulslänge
τ = 20 ns)
6.2.3 NOT–Gatter
Zur Konstruktion eines NOT–Gatters kann sowohl die Beeinflussung der Phase wie
auch der Amplitude verwendet werden.
Basierend auf dem XNOR–Gatter erhält man ein NOT, indem man an einen der
beiden Eingänge dauerhaft eine logische Null anlegt. Alternativ kann auch einer
der Wellenleiter durch ein einfaches Mikrowellenkabel mit einer geeigneten zusätzlichen Phasenverschiebung ersetzt werden. Wenn am Eingang eine logische Null
anliegt sind beide Signale in Phase; man erhält konstruktive Interferenz und damit
eine logische Eins am Ausgang. Fließt ein Strom von Iπ durch die Drahtschleife (logische Eins am Eingang) erhält man destruktive Interferenz und damit eine logische
Null am Ausgang.
Verwendet man die Spinwellenschalter anstelle der Phasenschieber (das heißt
also den NAND–Aufbau), kann man ebenfalls ein NOT–Gatter konstruieren. Dazu
muss an einem der beiden NAND–Eingänge dauerhaft eine logische Eins anliegen
oder alternative einer der beiden Wellenleiter ersatzlos entfernt werden. Liegt am
Eingang eine logische Null, kann das verbleibende Spinwellensignal propagieren,
man erhält eine logische Eins am Ausgang. Liegt eine logische Eins an, kann keine
Welle propagieren; es ergibt sich eine logische Null. Das beschriebene Verhalten in
beiden Fällen entspricht einem NOT–Gatter (siehe Tabelle 6.1(c)).
86
Spinwellenlogikgatter
Da beide Realisierungen als Spezialfälle des XNOR– und NAND–Gatters betrachtet werden können, entsprechen die Ausgangssignale des NOT–Gatters den in
den Abb. 6.4 und 6.5 gezeigten.
6.3 Spinwellenlogik mit einem Wellenleiter3
Bei den bisher vorgestellten Logikgattern wurden die Ein- und Ausgang des Interferometers durch Mikrowellenkomponenten realisiert. Insbesondere wurden Mikrowellensignale und nicht Spinwellen interferiert. Hier soll nun das Prinzip eines reinen Spinwelleninterferometer mit nur einem YIG–Wellenleiter vorgestellt werden.
Dieses vereinfacht den Aufbau von Logikgattern, da auf die Verwendung von zusätzlichen Mikrowellenleistungsteilern verzichtet werden kann. Gleichzeitig ist ein reines Spinwelleninterferometer kompatibel mit dem in [8] vorgeschlagenen Spinwellenbus.
6.3.1 Interferometer auf einem Wellenleiter
Abbildung 6.6 zeigt den Aufbau des verwendeten Interferometers auf einem Wellenleiter. Zur Vereinfachung wurde nur in einem der beiden Arme ein Phasenschieber
(wie in den bisherigen Experimenten realisiert als Drahtschleife) eingebaut. Dieses Interferometer kann damit nur als NOT–Gatter verwendet werden. Eine Erweiterung zu einem der anderen bisher beschriebenen Gatter ist allerdings leicht
möglich. Das Interferometer ist als “gabelförmige” Struktur aufgebaut und besteht
aus zwei Interferometer–Armen (den “Gabelzinken”) und einem Interferenzbereich,
in dem beide Signale überlappen können (dem “Gabelgriff”). Die gesamte Struktur ist 2,5 mm breit, zwischen den Armen ist eine Lücke von etwa 250 µm. Wie in
den bisherigen Experimenten wurde die Struktur aus einem YIG–Film (Dicke 8 µm)
aufgebaut.
Die Spinwellen in den beiden Armen werden durch dieselbe Mikrowellenantenne angeregt und sind daher näherungsweise in Phase.4 Innerhalb der Arme können
3 Die hier vorgestellten Struktur wurde in
Zusammenarbeit mit Alexander A. Serga entwickelt und
untersucht.
4 Da die Propagation der Spinwellen in den beiden Armen aufgrund geringfügiger Unterschiede in den Materialparametern und der Anregung der Spinwellen in den beiden Armen nicht exakt
identisch ist, kommt es in dem hier verwendeten Aufbau zu einem geringen Phasenunterschied zwischen beiden Armen. Dieser beeinflusst allerdings nicht die Funktionsweise des Interferometers als
Spinwellenlogikgatter.
6.3 Spinwellenlogik mit einem Wellenleiter
H0
87
I1
Abbildung 6.6: Aufbau eines Spinwellen Mach–Zehnder–Interferometer (Spinwellen NOT
Gate) mit einem Wellenleiter.
45,1 ns
45,1 ns
132,0 ns
132,0 ns
175,4 ns
175,4 ns
(a) In Phase
(b) Außer Phase
Abbildung 6.7: Orts- und zeitaufgelöste BLS–Messung des Spinwelleninterferometers. Die
Spinwellen werden in den Armen angeregt und propagieren in den Interferenzbereich, wo
sie überlagern. (a) Es fließt kein Strom durch die Drahtschleife, die beiden Spinwellenpulse
sind in Phase. Das Interferenzmuster zeigt ein klares Maximum in der Mitte der Struktur.
(b) Durch den Strom in der Drahtschleife ist die Spinwelle im unteren Arm um π phasenverschoben. Das Intereferenzmuster zeigt ein Minimum in der Mitte und jeweils ein Maximum
an beiden Seiten. (H0 = 1885 Oe, ω = 2π · 7,132 GHz, Pulslänge τ = 40 ns)
88
Spinwellenlogikgatter
Amplitude [dB]
0
-5
-10
-15
0
500
1000
1500
2000
Strom [mA]
Abbildung 6.8: Mikrowellensignal an der Ausgangsantenne des Intereferometers als Funktion des durch die Drahtschleife fließenden Stroms.
beide Pulse ungestört voneinander propagieren, um dann in der anschließenden Fläche zu interferieren. Das resultierende Muster kann mit Hilfe der ortsaufgelöste BLS
gemessen werden.
Abbildung 6.7(a) zeigt eine orts- und zeitaufgelöste BLS Messungen der Struktur
ohne einen an der Drahtschleife anliegenden Strom. Da beide Spinwellen in diesem
Fall näherungsweise in Phase sind, zeigt das Interferenzmuster ein klares Maximum
in der Mitte und kann als die erste (symmetrische) Breitenmode der Spinwelle verstanden werden. Wichtig für eine Anwendung dieses Konzepts ist dabei insbesonders, dass am Übergang von den Armen in die Interferenzfläche keine Rückreflexion
zu erkennen ist.
Fließt ein Strom durch die Drahtschleife, werden die beiden Signale gegeneinander phasenverschoben und das Interferenzmuster ändert sich. Abbildung 6.7(b) zeigt
dies für einen Strom, der einer Phasenverschiebung von π entspricht. In der Mitte
der Struktur findet sich nun ein Minimum, auf beiden Seiten der Struktur kann eine
Maximum beobachtet werden. Da die beide Maxima außer Phase sind, handelt es
sich dabei um die zweite (unsymmetrische) Breitenmode.
Durch das Anlegen eines Stroms kann das Ausgangssignal also von einer symmetrischen auf eine antisymmetrische Mode umgeschaltet werden. Definiert man
6.3 Spinwellenlogik mit einem Wellenleiter
89
45,1 ns
100,7 ns
121,6 ns
175,4 ns
Abbildung 6.9: Orts- und zeitaufgelöste BLS–Messung des Spinwellenleistungsteilers.
die logischen Eingangssignale wie in Kapitel 6.2.1, das heißt kein Strom entspricht
der logischen Null und Iπ entspricht der logischen Eins, so entspricht das Ausgangssignal dem eines logischen NOT–Gatters (siehe Tabelle 6.1(c)), wobei die symmetrische Mode als logische Eins und die antisymmetrische Mode als logische Null
interpretiert wird.
Die Ausgangsmode kann dabei optisch durch das BLS–Signal in der Mitte des
Wellenleiters ausgelesen werden. Alternativ kann auch eine zusätzliche Mikrowellenantenne verwendet werden (siehe Abb. 6.6). Da die beiden Maxima der unsymmetrische Mode außer Phase sind, beobachtet man in diesem Fall ein Minimum des
Mikrowellensignals.
Abbildung. 6.8 zeigt das gemessene Mikrowellensignal als Funktion des fließenden Stroms. Der deutliche Unterschied von fast 10 dB zwischen dem Minimum und
dem Ausgangssignal ohne fließenden Strom verdeutlicht noch einmal die Verwendbarkeit des Interferometers als NOT–Gatter.
6.3.2 Leistungsteiler auf einem Wellenleiter
Zum Aufbau einer reinen Spinwellenlogik wird neben dem bereits vorgestellten Interferometer noch ein Spinwellenleistungsteiler benötigt. Dieser soll ein ankommendes Spinwellensignal möglichst gleichmäßig auf zwei getrennte Arme verteilen.
Dieser Leistungsteiler kann sehr einfach durch Vertauschen von Ein- und Ausgangsantenne des vorgestellten Interferometers realisiert werden. Spinwellen werden dann im “Gabelgriff” angeregt und anschließend auf die “Zinken” aufgeteilt.
Abbildung 6.9 zeigt eine orts- und zeitaufgelöste BLS Messung dieses Prozesses.
Da die hier verwendete Mikrowellenantenne nicht perfekt symmetrisch konstruiert
ist, wird auch der ursprüngliche Spinwellenpuls nicht im Zentrum des Wellenleiters
angeregt. Trotzdem wird die Spinwelle in zwei vergleichbare Pulse geteilt. Weiter
beobachtet man auch hier keine sichtbare Rückreflexe am Übergang in die Arme.
Kapitel 7
Zusammenfassung und Ausblick
In der vorliegenden Arbeit wurden verschiedene Fragestellungen im Zusammenhang mit der Propagation und Anregung von mikrowellenangeregten Spinwellen in
Yttrium–Eisen–Granat untersucht. Besonderes Augenmerk lag dabei auf den Phaseneigenschaften der Spinwellen und der Beobachtung der freien Propagation von
Spinwellenpulsen.
Bei der Untersuchung von Spinwellen in Spinwellenwellenleitern konnten durch
die Messung der Phasenänderung der Spinwelle mit der Propagationsdistanz, der sogennanten Phasenakkumulation, neue Erkenntnisse im Bereich der Propagation und
Anregung von Spinwellen gewonnen werden. Anhand von Messungen an einer linearen Spinwelle und dem Vergleich der aus dieser Messung gewonnen Wellenlänge
mit Messungen der Phasenfronten, konnte die Anwendbarkeit dieses Verfahrens zur
Untersuchung von Spinwellen demonstriert werden.
Durch die Messungen der Phasenakkumulation von zwei gegenläufig propagierenden Spinwellen, die von demselben Mikrowellensignal angeregt wurden, konnte gezeigt werden, dass nicht nur die Symmetrie der Amplitude sondern auch die
der Phase dieser Spinwellen, von der verwendeten Geometrie abhängt. Backward–
Volume–Wellen, die parallel zum Magnetfeld propagieren, werden symmetrisch in
der Amplitude aber unsymmetrisch in der Phase, dass heißt mit einem Phasenunterschied von π, angeregt. Im Gegensatz dazu haben Surface–Wellen, die senkrecht
zum Feld propagieren und mit deutlich unterschiedlichen Amplituden angeregt werden, keinen Phasenunterschied. Theoretische Rechnungen konnten dieses Verhalten
bestätigen.
Bei der Propagation von nichtlinearen Spinwellen konnte ein direkter Einfluss
der Spinwellenamplitude auf die Spinwellenphase nachgewiesen werden. Diese
wird durch die Verkleinerung der statischen Magnetisierung durch einen intensiven
Spinwellenpuls und der daraus folgenden Änderung des Wellenvektors verursacht.
Durch die Dämpfung der Spinwellenintensität wird der Phasenunterschied zwischen
92
Zusammenfassung und Ausblick
dem linearen und dem nichtlinearen Anteil eines langen Spinwellenpulses nach einer Propagationsdistanz von einigen Millimetern konstant. Eine Messung dieses
Phasenunterschieds als Funktion der Propagationsdistanz erlaubte die Bestimmung
der Dämpfungszeit und des anfängliche Präzessionswinkels der Spinwelle.
Durch die Untersuchung der freien, zweidimensionalen Propagation eines Spinwellenpulses konnten die Auswirkungen der durch das externe Magnetfeld induzierten Anisotropie demonstriert werden. Diese Anisotropie erzeugt einen Bereich von
Wellenvektorwinkeln, in dem die Richtung der Spinwellenpropagation nicht von der
Richtung des Wellenvektors abhängig ist. Die Anregung von Spinwellen mit einem
ausreichend weiten Wellenvektorspektrum führt daher zur selbstständigen Ausbildung von lateral begrenzten Spinwellenstrahlen, den sogenannten Kaustikstrahlen.
Es konnte gezeigt werden, dass mit Hilfe einer Wellenleiterantenne eine kontrollierte
Anregung dieser Kaustikstrahlen möglich ist.
Der Einfluss der Stärke des externen Felds und der Breite der verwendeten Wellenleiterantenne auf die Kaustikstrahlen wurde untersucht. Anhand dieser Messungen wurde gezeigt, dass Kaustikstrahlen nur dann angeregt werden können, wenn
das Magnetfeld hinreichen klein und der Eingangswellenleiter hinreichend schmal
sind, da nur dann das Wellenvektorspektrum der angeregten Spinwelle weit genug
ausgedehnt ist.
Wie anhand der Messungen und theoretischer Rechnungen gezeigt werden konnte, propagieren die Kaustikstrahlen über makroskopische Distanzen ohne nennenswerte Verbreiterung, auch wenn ihre Breite vergleichbar oder sogar kleiner als ihre Wellenlänge ist. Im Experiment konnte ein stabiler Kaustikstrahl über mehr als
10 mm beobachtet werden; die Rechnungen lassen vermuten, dass eine Verbreiterung erst nach mehr als 10 cm eintreten würde. Phasenaufgelöste Messungen haben
gezeigt, dass wie zu erwarten war, Wellenvektor und Gruppengeschwindigkeit der
Kaustikstrahlen nicht parallel sind. Alle durchgeführten Messungen weisen eine gute qualitative Übereinstimmung mit den numerischen und analytischen Rechnungen
auf.
Die anisotrope Propagation von Spinwellen beeinflusst auch die Reflexion und
die Streuung von Kaustikstrahlen. Da die Richtung der Propagation ausschließlich
von der Richtung des externen Felds bestimmt wird, kann nicht–geometrische Reflexion beobachtet werden. Die Streuung eines Kaustikstrahls an einem mechanischen
Defekt ist aus diesem Grund ebenfalls stark anisotrop. Wie gezeigt wurde, werden in
diesem Fall neue Kaustikstrahlen entlang aller vier möglichen Richtungen angeregt.
Die Richtung der Kaustikstrahlen in Bezug auf die Geometrie der Probe kann dabei, ebenso wie bei der direkten Anregung, durch die Richtung des angelegten Felds
kontrolliert werden.
Prototypen von Spinwellenlogikgattern basierend auf einen Spinwelleninterferometer aus zwei YIG–Wellenleitern wurden getestet. Die Funktionsweise der grundlegenden Bauteile, einem Spinwellenphasenschieber und einem Spinwellenschalter,
Zusammenfassung und Ausblick
wurde demonstriert; die Funktion von XNOR–, NAND–, und NOT–Gattern konnte
realisiert werden.
Eine Konzept für Spinwellenlogik bestehend aus nur einem Wellenleiter wurde entwickelt. Die Funktion der aufgebauten Struktur als Spinwelleninterferometer
und als Spinwellenleistungsteiler wurde anhand von BLS Messungen demonstriert.
Ein einfaches NOT–Gatter basierend auf diesem Interferometer konnte konstruiert
werden.
Da die zum Aufbau der Gatter verwendeten Konzepte nicht vom verwendeten
Material abhängen, sollte eine Realisierung der Gatter auf der Basis von mikrometergroßen Permalloy Strukturen möglich sein.
Aufbauend auf der Beobachtung der (linearen) Spinwellen–Kaustikstrahlen kann
in Zukunft die Möglichkeit einer neuen zweidimensionalen, nichtlinearen Anregung
untersucht werden. Bei diesem sogenannten Kaustik–Soliton soll die Ausdehnung
des Spinwellenpulses entlang der Ausbreitungsrichtung durch den bereits bekannten nichtlinearen Effekt der Solitonenbildung stabilisiert werden. Die Stabilisierung
senkrecht dazu soll durch den hier beschriebenen Effekt der Kaustikanregung erreicht werden. In diesem Zusammenhangen können die Unterschiede und Gemeinsamkeiten des Kaustik–Solitons mit einer anderen zweidimensionalen nichtlinearen
Anregung, dem Spinwellen–Bullet [36, 39], dass in beiden Raumrichtungen durch
die Nichtlinearität stabilisiert wird, untersucht werden.
Es muss allerdings erwähnt werden, dass die Anregung eines Kaustik–Solitons
mit Hilfe der hier verwendeten Technik wahrscheinlich nicht möglich sein wird.
Damit die Intensität eines Kaustikstrahls hoch genug ist, um nichtlineare Effekte zu
beobachten, muss die ursprüngliche Spinwelle im Wellenleiter ebenfalls mit hoher
Intensität angeregt werden. Daher ist es sehr wahrscheinlich, dass es bereits während
der Propagation im Wellenleiter zur Ausbildung eines Solitons kommt. Erschwerend
kommt hinzu, dass die Energie der Spinwelle im Wellenleiter auf zwei Kaustikstrahlen aufgeteilt wird.
Die Lösung dieses Problems könnte in der direkten Anregung der Kaustikstrahlen durch eine Mikrostreifenantenne und ohne einen Eingangswellenleiter liegen.
Außerdem kann das externe Feld gegenüber der Normalen des Mikrostreifens gedreht werden, da, wie hier anhand der Anregung mit der Wellenleiternantenne gezeigt wurde, damit erreicht werden kann, dass einer der beiden Kaustikstrahlen mit
erhöhter Intensität angeregt wird. Da allerdings wie in dieser Arbeit gezeigt wurde eine sehr kurze Antenne benötigt wird, muss diese sehr wahrscheinlich in einem
mehrlagigen Aufbau realisiert werden. Außerdem ist bisher unklar, ob der Kaustikstrahl durch das Vorhandensein des magnetischen Wechselfelds der Antenne beeinflusst wird.
Sollten diese experimentellen Probleme gelöst werden können, muss weiter geklärt werden, inwieweit ein Soliton, das nicht parallel oder senkrecht zum Feld propagiert, stabil ist. Insbesondere muss untersucht werden, ob das Vorhandensein von
93
94
Zusammenfassung und Ausblick
Wellen mit verschieden gerichteten Wellenvektoren den Prozess der Solitonenbildung beeinflusst.
Bis zur ersten Beobachtung eines Kaustik–Solitons werden daher noch einige Probleme sowohl theoretischer wie auch experimenteller Natur zu lösen sein.
Die möglichen Realisierung eines stabilen zweidimensionalen Spinwellenpulses, der
durch zwei prinzipiell verschiedene Mechanismen stabilisiert wird, erscheint allerdings lohnenswert genug, diese Arbeit zu rechtfertigen.
Anhang A
Elektro–optischer Effekt
Zum Aufbau der phasenaufgelösten Brillouin–Lichtstreuspektroskopie (vgl. Kapitel 3.5) ist es nötig, dass ein Teil des eingestrahlten Lichts frequenzverschoben wird.
Dazu wird hier ein elektrooptischer Modulator verwendet, dessen Funktion auf dem
sogenannten elektrooptischen Effekt basiert. Dieser beschreibt die Änderung des
Brechungsindex einiger Kristalle (wie zum Beispiel dem hier verwendeten Lithiumniobat LiNbO3 ) durch ein angelegtes elektrisches Feld. Für Licht, das parallel zu
einer der optischen Achsen des Kristalls polarisiert ist, wird diese Änderung durch
∆n =
n30
rE
2
(A.1)
beschrieben. Dabei ist E das angelegte elektrische Feld, n0 der Brechungsindex des
Kristalls ohne elektrisches Feld und r das wirksame Element des elektro–optischen
Tensors (siehe zum Beispiel [134, Kapitel 9]).
Abbildung A.1 veranschaulicht das Koordinatensystem für die folgende Rechnung. Licht der Frequenz ωL mit dem Wellenvektor k0 propagiert entlang der y–
Achse durch einen Kristall der Länge l. Die elektrische Feldkomponente
Ein (t) = Aei(ωLt−k0 y)
(A.2)
des einfallenden Lichtes und das angelegte elektrische Feld
E(t) = Em sin (ωmt)
(A.3)
sind entlang der x–Achse orientiert1.
1 Bei dem im Rahmen dieser Arbeit verwendeten Modulator liegt ω
m
im Bereich von einigen GHz,
daher ist der LiNbO3 –Kristall in einem Hohlraumresonator eingebaut, der mit einem entsprechenden
Mikrowellensignal betrieben wird.
96
Elektro–optischer Effekt
ωL
y=l
E = Em sin (ωmt)
ωL − ωm
LiNbO3
ωL + ωm
y=0
ωL
y
z
x
Abbildung A.1: Prinzip der Elektro–optische Modulation.
Für den Wellenvektor kn des Lichts innerhalb des Kristalls gilt dann mit der Vakuumlichtgeschwindigkeit c und unter Verwendung von Gl. (A.1)
n30
ωL
ωL
kn =
(n0 + ∆ n) =
n0 + rE(t)
.
(A.4)
c
c
2
Für die elektrische Feldkomponente Eout nach der Propagation ergibt sich damit
Eout (t) = A exp [i (ωLt − kn l − k0 (y − l))]
n30
ω
= A exp i ωLt −
n0 + rEm sin (ωmt) l − k0 (y − l)
c
2
(A.5)
.
(A.6)
Der konstante Phasenterm −n0 l ωL /c + k0 l ist für die weitere Betrachtung ohne Bedeutung und kann als Teil der (komplexen) Amplitude A′ betrachtet werden, so dass
sich Gl. (A.6) zu
Eout (t) = A′ ei(ωLt−k0 y) eiδ sin(ωmt)
(A.7)
mit
ωL n30 rEm l
(A.8)
2c
vereinfacht. Unter Verwendung der Bessel–Funktionen Jn [114] und der Relation
δ =−
eiδ sin (ωmt) =
∞
∑
n=−∞
Jn (δ )einωmt
(A.9)
Elektro–optischer Effekt
97
(aus [135, S. 108]) kann man Gl. (A.7) zu
Eout (t) = A′ e−ik0 y
∞
∑
Jn (δ )ei(ωL +nωm )t
(A.10)
n=−∞
umformen. Durch die Modulation erhält das eingestrahlte monochromatische Licht
also Komponenten bei den Frequenzen ωL ± nωm .
Anhang B
Messung der
Spinwellen–Phasenprofile
Im Folgenden soll die hier verwendete Technik zur Bestimmung der Phasenprofile
einer Spinwelle erläutert werden. Dazu wird zunächst der zugrundeliegende Algorithmus hergeleitet, um dann anschließend die darauf aufbauende Messtechnik
vorzustellen.
B.1 Berechnung
Die zu untersuchende Spinwelle s(t) kann in der Form
mit
s(t,x) = p(t,x)eiω t
(B.1)
p(t,x) = P(t,x)eiϕ (t,x)
(B.2)
dargestellt werden. Auf die Darstellung der Ortskoordinaten wird im folgenden zugunsten einer besseren Lesbarkeit verzichtet. P(t) ist die (reelle) Einhüllende des
Spinwellenpakets (d.h. das Amplitudenprofil), ϕ (t) ist das Phasenprofil. Ein zeitaufgelöste BLS Messung dieser Welle liefert die Größe |p(t)|2 = P(t)2 und damit nur
Informationen über die Amplitude und nicht über die Phase.
Zur Messung des Phasenprofils benötigt man daher noch zwei Referenzsignale
r1 (t) und r2 (t). Diese werden so gewählt, dass der Phasenunterschied zwischen r1 (t)
und r2 (t) π/2 beträgt und die Amplituden gleich groß sind. Ist R(t) diese Amplitude
(der Einfachheit halber üblicherweise ein Rechteckspuls), so erhält man
r1 (t) = R(t)ei0eiω t = R(t)eiω t
(B.3)
100
Messung der Spinwellen–Phasenprofile
sowie
r2 (t) = R(t)eiπ/2eiω t = iR(t)eiω t
.
(B.4)
Eine direkte zeitaufgelöste Messung von r1 (t) und r2 (t) liefert in beiden Fällen
die Größe R(t)2. Überlagert man r1,2 (t) mit s(t), erhält man die Interferenzbilder
I1 (t)2 = |s(t) + r1(t)|2 und I2 (t)2 = |s(t) + r2(t)|2 . Umformung dieser Ausdrücke
unter Berücksichtigung von P(t)2 = |p(t)|2 = Re (p(t))2 + Im (p(t))2 liefert für I1 (t)
I1 (t)2 = |s(t) + r1(t)|2
2
iω t
iω t = p(t)e + R(t)e = |p(t) + R(t)|2
= |Re(p(t)) + i Im(p(t)) + R(t)|2
= [Re (p(t)) + R(t)]2 + Im (p(t))2
= Re (p(t))2 + 2 Re (p(t))R(t) + R(t)2 + Im (p(t))2
= P(t)2 + 2 Re (p(t)) R(t) + R(t)2
(B.5)
und analog für I2 (t)
I2 (t)2 = |s(t) + r2(t)|2
2
iω t
iω t = p(t)e + iR(t)e = |p(t) + iR(t)|2
= |Re(p(t)) + i Im(p(t)) + iR(t)|2
= Re (p(t))2 + [Im (p(t)) + R(t)]2
= Re (p(t))2 + Im (p(t))2 + 2 Im (p(t))R(t) + R(t)2
= P(t)2 + 2 Im (p(t)) R(t) + R(t)2
.
(B.6)
Aus Gl. (B.5) und (B.6) erhält man Ausdrücke für den Real- und Imaginärteil
von p(t)
I12 (t) − P(t)2 − R(t)2
p
2 R(t)2
I 2 (t) − P(t)2 − R(t)2
p
Im (p(t)) = 2
2 R(t)2
Re (p(t)) =
(B.7)
.
(B.8)
Da alle in diesen beiden Gleichung vorkommenden Größen (I1,2 (t)2, P(t)2 und
R(t)2) aus zeitaufgelösten BLS Messungen gewonnen werden können, erhält man
Messung der Spinwellen–Phasenprofile
101
daraus das gesuchte Phasenprofil ϕ (t)
ϕ (t) = arctan
Im (p(t))
+ nπ
Re (p(t))
(B.9)
Im
mit


−1
n = +1


0
wenn Re (p(t)) < 0 und Im (p(t)) < 0,
wenn Re (p(t)) < 0 und Im (p(t)) ≥ 0,
wenn Re (p(t)) ≥ 0
+π ±0
−π ±0
Re
Bei den so gewonnen Phasenprofilen ist zu beachten, dass die Phase nur bis auf
Vielfache von 2π definiert ist und daher bei der Auswertung (insbesondere bei der
Messung der Phasenakkumulation (siehe Kapitel 4) geeignete Vielfache von 2π addiert beziehungsweise subtrahiert werden müssen.
B.2 Messung
Prinzipiell können alle zur Berechnung von ϕ (t) benötigten Größen (P(t)2, I1 (t)2,
I2 (t)2 und R(t)2) durch vier einzelne zeitaufgelöste BLS–Messungen gewonnen werden. Das im Rahmen dieser Arbeit verwendete Verfahren hat demgegenüber zum
einen den Vorteil einer höheren Genauigkeit, da eventuelle Änderungen der BLS–
Zählraten aufgrund von Änderungen der Interferometerstabilität oder der Laserleistung kompensiert werden, und zum anderen den eines reduzierten Zeitbedarfs, da
nur drei Messungen nötig sind.
Die Grundidee besteht darin, das Referenzsignal R(t) aus zwei (zeitlich getrennten) Rechteckspulsen zusammenzusetzen. Der erste Puls (im Folgenden R1 (t)) liegt
dabei in demselben Zeitraum an, in dem p(t) 6= 0 sein kann, während der zweite
Puls (im Folgenden R2 (t)) etwas später eingeschaltet wird und keinerlei zeitlichen
Überlapp mit p(t) haben darf. Weiter ist wichtig, dass beide Pulse dieselbe Amplitude haben und getrennt voneinander ein- und ausgeschaltet werden können (das heißt
Messungen, bei denen nur der zweite Puls anliegt, müssen realisierbar sein). Die
Messung besteht dann aus folgenden drei Einzelmessungen:
1. Messung von P(t)2: R1 (t) wird aus-, R2 (t) eingeschaltet, das heißt, es wird
nur die Spinwelle P(t)2 und der zweite Referenzpuls R2 (t)2 gemessen (Siehe
Abb. B.1(a)).
2. Messung von I1 (t)2: R1 (t) und R2 (t) werden eingeschaltet, das heißt, es
wird die Interferenz I1 (t)2 und der zweite Referenzpuls R2 (t)2 gemessen (Siehe Abb. B.1(b)).
Messung der Spinwellen–Phasenprofile
Intensität [a.u.]
102
R2 (t)2
P(t)2
0
200
400
600
800
1000
1200
1400
1600
1400
1600
1400
1600
Zeit [ns]
Intensität [a.u.]
(a) 1. Messung
I1 (t)2
0
200
400
R2 (t)2
600
800
1000
1200
Zeit [ns]
Intensität [a.u.]
(b) 2. Messung
I2 (t)2
0
200
400
R2 (t)2
600
800
1000
1200
Zeit [ns]
(c) 3. Messung
Abbildung B.1: Beispiel für die zur Berechnung des Phasenprofils notwendigen Messungen
3. Messung von I2 (t)2: R1 (t) und R2 (t) werden eingeschaltet, allerdings wird
im Vergleich zur 2. Messung eine zusätzliche Phasenverschiebung von π/2
installiert, das heißt es wird die Interferenz I2 (t)2 und der zweite Referenzpuls
R2 (t)2 gemessen (Siehe Abb. B.1(c)).
Da bei allen drei Messungen R2 (t) die gleiche Intensität hat, werden die Messungen auf den leicht zu bestimmenden Wert von R2 (t)2 normiert. Dadurch ergibt
sich für die weitere Rechnung R(t) = 1. Außerdem werden eventuelle Intensitätsschwankungen kompensiert, da diese R2 (t) genauso wie alle anderen Signale (P(t)2,
I1 (t)2 und I2 (t)2) beeinflussen. Die weitere Rechnung erfolgt wie in B.1 skizziert.
Um die Messung weiter zu vereinfachen, werden die drei Einzelmessungen üblicherweise nicht nur in einem Punkt durchgeführt, sondern jeweils ein vollständiger
orts- und zeitaufgelöster Scan der Probe durchgeführt. Die Auswertung (d.h. Ein-
Messung der Spinwellen–Phasenprofile
103
lesen, Normalisieren und Aufteilen der Rohdaten sowie das Berechnen der Phasenprofile und Phasenakkumulation) wird anschließend von einem im Rahmen dieser
Arbeit entwickelten LabView–Programm vorgenommen.
Eigene Veröffentlichungen
[A1] T. Schneider, Bestimmung und Beeinflussung der Phaseneigenschaften von
Spinwellenn in Yttrium-Eisen-Granat-Wellenleiterstrukturen, Diplomarbeit,
Fachbereich Physik, TU Kaiserslautern (2005).
[A2] M. P. Kostylev, A. A. Serga, T. Schneider, B. Leven, B. Hillebrands, Spin-wave
logical gates, Appl. Phys. Lett. 87, 153501 (2005).
[A3] A. A. Serga, T. Schneider, B. Hillebrands, S. O. Demokritov, M. P. Kostylev, Phase-sensitive Brillouin light scattering spectroscopy from spin-wave
packets, Appl. Phys. Lett. 89, 063506 (2006).
[A4] A. A. Serga, T. Schneider, B. Hillebrands, M. P. Kostylev, A. N. Slavin, Shaping of microwave pulses using phase-sensitive spin-wave amplifier, Appl.
Phys. Lett. 90, 022502 (2007).
[A5] T. Schneider, A. A. Serga, B. Hillebrands, M. P. Kostylev, Linear and nonlinear phase accumulation of backward volume magnetostatic spin waves in
yttrium-iron-garnet spin-wave waveguides, Europhys. Lett. 77, 57002 (2007).
[A6] M. P. Kostylev, A. A. Serga, T. Schneider, T. Neumann, B. Leven, B. Hillebrands, R. L. Stamps, Resonant and nonresonant scattering of dipoledominated spin waves from a region of inhomogeneous magnetic field in a
ferromagnetic film, Phys. Rev. B 76, 184419 (2007).
[A7] T. Schneider, A. A. Serga, B. Leven, B. Hillebrands, R. L. Stamps, M. P.
Kostylev, Realization of spin-wave logic gates, Appl. Phys. Lett. 92, 022505
(2008).
[A8] T. Schneider, A. Serga, B. Hillebrands, M. Kostylev, Spin-wave ferromagnetic film combiner as a NOT logic gate, J. Nanoelectron. Optoelectron. 3, 69
(2008).
106
Eigene Veröffentlichungen
[A9] T. Schneider, A. A. Serga, T. Neumann, B. Hillebrands, M. P. Kostylev, Phase
reciprocity of spin-wave excitation by a microstrip antenna, Phys. Rev. B 77,
214411 (2008).
[A10] F. Fohr, A. A. Serga, T. Schneider, J. Hamrle, B. Hillebrands, Phase sensitive Brillouin scattering measurements with a novel magneto-optic modulator,
Review of Scientific Instruments 80, 043903 (2009).
[A11] T. Neumann, T. Schneider, A. A. Serga, B. Hillebrands, An EOM-assisted
wave-vector-resolving Brillouin light scattering setup, Rev. Sci. Instrum.
(2009), im Druck.
[A12] T. Schneider, A. A. Serga, A. V. Chumak, B. Hillebrands, C. W. Sandweg,
S. Wolff, M. P. Kostylev, V. S. Tiberkevich, A. J. Slavin, Non-diffractive spin
wave beams: channeled wave propagation in a medium with controlled anisotropy (2009), in Vorbereitung.
Literaturverzeichnis
[1] J. R. Eshbach, Spin-Wave Propagation and the Magnetoelastic Interaction in
Yttrium Iron Garnet, Phys. Rev. Lett. 8, 357 (1962).
[2] J. R. Eshbach, Spin-Wave Propagation and the Magnetoelastic Interaction in
Yttrium Iron Garnet, J. Appl. Phys. 34, 1298 (1963).
[3] O. Gaier, J. Hamrle, S. J. Hermsdoerfer, H. Schultheiß, B. Hillebrands, Y. Sakuraba, M. Oogane, Y. Ando, Influence of the L2(1) ordering degree on the
magnetic properties of Co2MnSi Heusler films, J. Appl. Phys. 103, 103910
(2008).
[4] M. Belmeguenai, F. Zighem, Y. Roussigné, S.-M. Chérif, P. Moch, K. Westerholt, G. Woltersdorf, G. Bayreuther, Microstrip line ferromagnetic resonance and Brillouin light scattering investigations of magnetic properties of
Co2MnGe Heusler thin films, Phys. Rev. B 79, 024419 (2009).
[5] J. Adam, Analog signal processing with microwave magnetics, P. IEEE 76, 159
(1988).
[6] W. Ishak, Magnetostatic wave technology: a review, P. IEEE 76, 171 (1988).
[7] R. Hertel, W. Wulfhekel, J. Kirschner, Domain-Wall Induced Phase Shifts in
Spin Waves, Phys. Rev. Lett. 93, 257202 (2004).
[8] A. Khitun, K. L. Wang, Nano scale computational architectures with Spin Wave
Bus, Superlattice. Microst. 38, 184 (2005).
[9] A. Khitun, M. Bao, K. Wang, Spin Wave Magnetic NanoFabric: A New Approach to Spin-Based Logic Circuitry, IEEE T.Magn. 44, 2141 (2008).
[10] S. V. Vasiliev, V. V. Kruglyak, M. L. Sokolovskii, A. N. Kuchko, Spin wave
interferometer employing a local nonuniformity of the effective magnetic field,
J. Appl. Phys. 101, 113919 (2007).
108
Literaturverzeichnis
[11] K.-S. Lee, S.-K. Kim, Conceptual design of spin wave logic gates based on a
Mach–Zehnder-type spin wave interferometer for universal logic functions, J.
Appl. Phys. 104, 053909 (2008).
[12] A. Khitun, R. Ostroumov, K. L. Wang, Spin-wave utilization in a quantum
computer, Phys. Rev. A 64, 062304 (2001).
[13] C. W. Sandweg, S. J. Hermsdoerfer, H. Schultheiss, S. Schafer, B. Leven,
B. Hillebrands, Modification of the thermal spin-wave spectrum in a Ni81Fe19
stripe by a domain wall, J. Phys. D Appl.Phys. 41, 164008 (2008).
[14] D.-S. Han, S.-K. Kim, J.-Y. Lee, S. J. Hermsdoerfer, H. Schultheiss, B. Leven, B. Hillebrands, Magnetic domain-wall motion by propagating spin waves,
Appl. Phys. Lett. 94, 112502 (2009).
[15] L. Berger, Emission of spin waves by a magnetic multilayer traversed by a
current, Phys. Rev. B 54, 9353 (1996).
[16] J. C. Slonczewski, Current-driven excitation of magnetic multilayers, J. Magn.
Magn. Mater. 159, L1 (1996).
[17] A. Slavin, V. Tiberkevich, Spin Wave Mode Excited by Spin-Polarized Current
in a Magnetic Nanocontact is a Standing Self-Localized Wave Bullet, Phys.
Rev. Lett. 95, 237201 (2005).
[18] V. E. Demidov, S. O. Demokritov, G. Reiss, K. Rott, Effect of spin-polarized
electric current on spin-wave radiation by spin-valve nanocontacts, Appl.
Phys. Lett. 90, 172508 (2007).
[19] V. Tiberkevich, A. Slavin, J.-V. Kim, Microwave power generated by a spintorque oscillator in the presence of noise, Appl. Phys. Lett. 91, 192506 (2007).
[20] G. Woltersdorf, O. Mosendz, B. Heinrich, C. H. Back, Magnetization Dynamics due to Pure Spin Currents in Magnetic Double Layers, Phys. Rev. Lett.
99, 246603 (2007).
[21] V. Vlaminck, M. Bailleul, Current-Induced Spin-Wave Doppler Shift, Science
322, 410 (2008).
[22] S. O. Demokritov, B. Hillebrands, A. N. Slavin, Brillouin Light Scattering Studies of Confined Spin Waves: Linear and Nonlinear Confinement, Phys. Rep.
348, 441 (2001).
Literaturverzeichnis
109
[23] K. Perzlmaier, M. Buess, C. H. Back, V. E. Demidov, B. Hillebrands, S. O. Demokritov, Spin-Wave Eigenmodes of Permalloy Squares with a Closure Domain
Structure, Phys. Rev. Lett. 94, 057202 (2005).
[24] C. Bayer, Das Spinwellen-Eigenspektrum in homogen und inhomogen magnetisierten Strukturen und periodeischen Übergittern, Dissertation, Fachbereich
Physik, TU Kaiserslautern (2006).
[25] S. Mendach, J. Podbielski, J. Topp, W. Hansen, D. Heitmann, Spin-wave confinement in rolled-up ferromagnetic tubes, Appl. Phys. Lett. 93, 262501 (2008).
[26] A. V. Chumak, A. A. Serga, B. Hillebrands, M. P. Kostylev, Scattering of backward spin waves in a one-dimensional magnonic crystal, Appl. Phys. Lett. 93,
022508 (2008).
[27] S. A. Nikitov, P. Tailhades, C. S. Tsai, Spin waves in periodic magnetic structures - magnonic crystals, J. Magn. Magn. Mater. 236, 320 (2001).
[28] G. Gubbiotti, S. Tacchi, G. Carlotti, N. Singh, S. Goolaup, A. O. Adeyeye,
M. Kostylev, Collective spin modes in monodimensional magnonic crystals
consisting of dipolarly coupled nanowires, Appl. Phys. Lett. 90, 092503
(2007).
[29] M. Kostylev, P. Schrader, R. L. Stamps, G. Gubbiotti, G. Carlotti, A. O.
Adeyeye, S. Goolaup, N. Singh, Partial frequency band gap in one-dimensional
magnonic crystals, Appl. Phys. Lett. 92, 132504 (2008).
[30] M. Krawczyk, Magnetostatic Waves in One-Dimensional Magnonic Crystals
With Magnetic and Nonmagnetic Components, IEEE T. Magn. 44, 2854 (2008).
[31] K.-S. Lee, D.-S. Han, S.-K. Kim, Physical Origin and Generic Control of Magnonic Band Gaps of Dipole-Exchange Spin Waves in Width-Modulated Nanostrip Waveguides, Phys. Rev. Lett. 102, 127202 (2009).
[32] M. Chen, M. A. Tsankov, J. M. Nash, C. E. Patton, Microwave magneticenvelope dark solitons in yttrium iron garnet thin films, Phys. Rev. Lett. 70,
1707 (1993).
[33] M. A. Tsankov, M. Chen, C. E. Patton, Forward volume wave microwave envelope solitons in yttrium iron garnet films: Propagation, decay, and collision,
J. Appl. Phys. 76, 4274 (1994).
[34] M. Chen, M. A. Tsankov, J. M. Nash, C. E. Patton, Backward-volume-wave
microwave-envelope solitons in yttrium iron garnet films, Phys. Rev. B 49,
12773 (1994).
110
Literaturverzeichnis
[35] N. G. Kovshikov, B. A. Kalinikos, C. E. Patton, E. S. Wright, J. M. Nash, Formation, propagation, reflection, and collision of microwave envelope solitons
in yttrium iron garnet films, Phys. Rev. B 54, 15210 (1996).
[36] M. Bauer, O. Büttner, S. O. Demokritov, B. Hillebrands, V. Grimalsky, Y. Rapoport, A. N. Slavin, Observation of Spatiotemporal Self-Focusing of Spin Waves in Magnetic Films, Phys. Rev. Lett. 81, 3769 (1998).
[37] J. M. Nash, P. Kabos, R. Staudinger, C. E. Patton, Phase profiles of microwave
magnetic envelope solitons, J. Appl. Phys. 83, 2689 (1998).
[38] O. Büttner, M. Bauer, S. O. Demokritov, B. Hillebrands, M. P. Kostylev, B. A.
Kalinikos, A. N. Slavin, Collisions of Spin Wave Envelope Solitons and SelfFocused Spin Wave Packets in Yttrium Iron Garnet Films, Phys. Rev. Lett. 82,
4320 (1999).
[39] A. A. Serga, S. O. Demokritov, B. Hillebrands, A. N. Slavin, Self-Generation
of Two-Dimensional Spin-Wave Bullets, Phys. Rev. Lett. 92, 117203 (2004).
[40] Y. S. Kivshar, G. P. Agrawal, Optical Solitons, Academic Press, Amsterdam,
Boston, London, New York, Oxford, Paris, San Diego, San Francisco, Singapore, Sydney, Tokyo (2003).
[41] S. O. Demokritov, A. A. Serga, V. E. Demidov, B. Hillebrands, M. P. Kostylev, B. A. Kalinikos, Experimental observation of symmetry-breaking nonlinear modes in an active ring, Nature 426, 159 (2003).
[42] A. A. Serga, M. P. Kostylev, B. A. Kalinikos, S. O. Demokritov, B. Hillebrands,
H. Benner, Parametric Generation of Solitonlike Spin-Wave Pulses in Ring Resonators Based on Ferromagnetic Films, JETP Lett. 77, 300 (2003).
[43] S. O. Demokritov, V. E. Demidov, O. Dzyapko, G. A. Melkov, A. A. Serga,
B. Hillebrands, A. N. Slavin, Bose-Einstein condensation of quasi-equilibrium
magnons at room temperature under pumping, Nature 443, 430 (2006).
[44] A. V. Bagada, G. A. Melkov, A. A. Serga, A. N. Slavin, Parametric Interaction
of Dipolar Spin Wave Solitons with Localized Electromagnetic Pumping, Phys.
Rev. Lett. 79, 2137 (1997).
[45] G. A. Melkov, A. A. Serga, V. S. Tiberkevich, A. N. Oliynyk, A. N. Slavin,
Wave Front Reversal of a Dipolar Spin Wave Pulse in a Nonstationary ThreeWave Parametric Interaction, Phys. Rev. Lett. 84, 3438 (2000).
Literaturverzeichnis
111
[46] G. A. Melkov, A. A. Serga, V. S. Tiberkevich, Y. V. Kobljanskij, A. N. Slavin,
Nonadiabatic interaction of a propagating wave packet with localized parametric pumping, Phys. Rev. E 63, 066607 (2001).
[47] A. A. Serga, A. V. Chumak, A. André, G. A. Melkov, A. N. Slavin, S. O. Demokritov, B. Hillebrands, Parametrically Stimulated Recovery of a Microwave
Signal Stored in Standing Spin-Wave Modes of a Magnetic Film, Phys. Rev.
Lett. 99, 227202 (2007).
[48] K. R. Smith, V. I. Vasyuchka, M. Wu, G. A. Melkov, C. E. Patton, Cloning and
trapping of magnetostatic spin-wave pulses by parametric pumping, Phys. Rev.
B 76, 054412 (2007).
[49] S. Schäfer, A. V. Chumak, A. A. Serga, G. A. Melkov, B. Hillebrands, Microwave spectral analysis by means of nonresonant parametric recovery of spinwave signals in a thin magnetic film, Appl. Phys. Lett. 92, 162514 (2008).
[50] A. V. Chumak, A. A. Serga, B. Hillebrands, G. A. Melkov, V. Tiberkevich,
A. N. Slavin, Parametrically stimulated recovery of a microwave signal using
standing spin-wave modes of a magnetic film, Phys. Rev. B 79, 014405 (2009).
[51] T. Neumann, A. A. Serga, B. Hillebrands, Probing of a parametrically pumped
magnon gas with a nonresonant packet of traveling spin waves, Appl. Phys.
Lett. 93, 252501 (2008).
[52] A. A. Serga, S. O. Demokritov, B. Hillebrands, S.-G. Min, A. N. Slavin, Phase
control of nonadiabatic parametric amplification of spin wave packets, J. Appl.
Phys. 93, 8585 (2003).
[53] V. Veerakumar, R. Camley, Focusing of Spin Waves in YIG Thin Films, IEEE
T. Magn. 42, 3318 (2006).
[54] V. Veerakumar, R. E. Camley, Magnon focusing in thin ferromagnetic films,
Phys. Rev. B 74, 214401 (2006).
[55] S. Chikazumi, Physics of Ferromagnetism, Oxford University Press, New York,
zweite Auflage (1999).
[56] A. Aharoni, Introduction to the Theory of Ferromagnetism, Clarendon Press,
Oxford, zweite Auflage (2001).
[57] A. G. Gurevich, G. A. Melkov, Magnetization Oscillations and Waves, CRC
Press, New York (1996).
112
Literaturverzeichnis
[58] D. D. Stancil, Theory of Magnetostatic Waves, Springer-Verlag, New York,
Berlin, Heidelberg (1993).
[59] C. E. Patton, Magnetic excitations in solids, Phys. Rep. 103, 251 (1984).
[60] A. S. Arrot, Magnetism in SI and Gaussian Units, in J. A. C. Bland, B. Heinrich
(Hrsg.), Ultrathin Magnetic Structures I, Springer-Verlag, Berlin, Heidelberg,
New York (1994).
[61] J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, New York, dritte
Auflage (1998).
[62] R. C. O’Handley, Modern Magnetic Materials, Principles and Apllications,
John Wiley & Sons, New York, Chichester, Weinheim, Brisbane, Singapore,
Toronto (2000).
[63] B. Hillebrands, S. Blügel, Magnetismus, in Festkörper, Band 6 von Bergmann,
Schäfer: Lehrbuch der Experimentalphysik, de Gruyter, Berlin, zweite Auflage
(2005).
[64] W. Heisenberg, Zur Theorie des Ferromagnetismus, Z. Phys. A - Hadron. Nucl.
49, 619 (1928).
[65] C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantenmechanik, Band 2, Walter de
Gruyter, Berlin, New York, zweite Auflage (1999).
[66] L. Landau, E. Lifshitz, On the theory of the dispersion of magnetic permeability
in ferromagnetic bodies, Phys. Z. Sowjetunion 8, 153 (1935).
[67] J. Mallinson, On damped gyromagnetic precession, IEEE T. Magn. 23, 2003
(1987).
[68] T. L. Gilbert, A phenomenological theory of damping in ferromagnetic materials, IEEE T. Magn. 40, 3443 (2004).
[69] H. Ibach, H. Lüth, Festkörperphysik, Springer-Verlag, Berlin, Heidelberg, New
York, 6. Auflage (2002).
[70] M. J. Hurben, C. E. Patton, Theory of magnetostatic waves for in-plane magnetized isotropic films, J. Magn. Magn. Mater. 139, 263 (1995).
[71] R. W. Damon, J. R. Eshbach, Magnetostatic Modes of a Ferromagnetic Slab, J.
Appl. Phys. 31, 104S (1960).
[72] R. W. Damon, J. R. Eshbach, Magnetostatic Modes of a Ferromagnetic Slab, J.
Phys. Chem. Solids 19, 308 (1960).
Literaturverzeichnis
113
[73] L. R. Walker, Magnetostatic Modes in Ferromagnetic Resonance, Physical Review 105, 390 (1957).
[74] C. Kittel, Interpretation of anomalous larmor frequencies in ferromagnetic resonance experiments, Phys. Rev. 71, 270 (1947).
[75] C. Kittel, On the theory of ferromagnetic resonance absorption, Phys. Rev. 73,
155 (1948).
[76] J. H. van Vleck, Concerning the theory of ferromagnetic ressonance absorption, Phys. Rev. 78, 266 (1950).
[77] I. N. Bronstein, K. A. Semendjaev, G. Musiol, H. Mühlig, Taschenbuch der Mathematik, Verlag Harri Deutsch, Thun und Frankfurt am Main, fünfte Auflage
(2000).
[78] J. R. Eshbach, R. W. Damon, Surface Magnetostatic Modes and Surface Spin
Waves, Phys. Rev. 118, 1208 (1960).
[79] T. Neumann, persönliche Mitteilung.
[80] B. Hillebrands, J. Hamrle, Investigation of Spin Waves and Spin Dynmaics by
Optical Techniques, in Handbook of Magnetism and Advanced Magnetic Material, Band 3, John Wiley & Sons, New York, Chichester, Weinheim, Brisbane,
Singapore, Toronto, erste Auflage (2007).
[81] M. Rohmer, Untersuchungen an mikrowellenangeregten Spinwellen, Diplomarbeit, Fachbereich Physik, Universität Kaiserslautern (1998).
[82] G. Nimtz, Mikrowellen - Einführung in Theorie und Anwendung, BI Wissenschaftsverlag, Manheim, Wien, Zürich, zweite Auflage (1990).
[83] D. V. Morgan, M. J. Howes (Hrsg.), Microwave solid state devices and applications, Peter Peregrinus Ltd., Stevenage, UK, New York (1980).
[84] V. Cherepanov, I. Kolokolov, V. L’vov, The saga of YIG: Spectra, thermodynamics, interaction and relaxation of magnons in a complex magnet, Phys. Rep.
229, 81 (1993).
[85] T. Wittkowski, Brillouin-Lichtstreuuntersuchungen an Bornitridschichten, Dissertation, Fachbereich Physik, Universität Kaiserslautern (2002).
[86] P. Grünberg, C. Mayr, W. Vach, M. Grimsditch, Determination of magnetic
parameters by means of brillouinscattering. Examples: Fe, Ni, Ni0.8Fe0.2, J
Magn. Magn. Mater. 28, 319 (1982).
114
Literaturverzeichnis
[87] P. Grünberg, R. Schreiber, Y. Pang, M. B. Brodsky, H. Sowers, Layered Magnetic Structures: Evidence for Antiferromagnetic Coupling of Fe Layers across Cr
Interlayers, Phys. Rev. Lett. 57, 2442 (1986).
[88] H. Yan Zhang, P. Kabos, H. Xia, P. A. Kolodin, C. E. Patton, Brillouin lightscattering observation of the nonlinear spin-wave decay in yttrium iron garnet
thin films, Phys. Rev. B 61, 522 (2000).
[89] G. Gubbiotti, G. Carlotti, T. Okuno, M. Grimsditch, L. Giovannini, F. Montoncello, F. Nizzoli, Spin dynamics in thin nanometric elliptical Permalloy dots: A
Brillouin light scattering investigation as a function of dot eccentricity, Phys.
Rev. B 72, 184419 (2005).
[90] H. Schultheiss, S. Schäfer, P. Candeloro, B. Leven, B. Hillebrands, A. N. Slavin, Observation of Coherence and Partial Decoherence of Quantized Spin
Waves in Nanoscaled Magnetic Ring Structures, Phys. Rev. Lett. 100, 047204
(2008).
[91] W. Nolting, Quantenmechanik - Methoden und Anwendungen, Band 5/2 von
Grundkurs Theoretische Physik, Springer-Verlag, Berlin, Heidelberg, New
York, fünfte Auflage (2004).
[92] B. Hillebrands, Brillouin light scattering from layered magnetic structures, in
M. Cardona, G. Güntherodt (Hrsg.), Light scattering in solids VII. Crystal field
and magnetic excitations, Band 75 von Topics in applied physics, SpringerVerlag, Berlin, Heidelberg, New York (2000).
[93] M. G. Cottam, D. J. Lockwood, Light Scattering in Magnetic Solids, John Wiley & Sons, New York, Chichester, Weinheim, Brisbane, Singapore, Toronto
(1986).
[94] P. A. Fleury, R. Loudon, Scattering of Light by One- and Two-Magnon Excitations, Phys. Rev. 166, 514 (1968).
[95] J. R. Sandercock, Trends in Brillouin Scattering: Studies of Opaque Materials,
Supported Films, and Central Modes, in M. Cardona, G. Güntherodt (Hrsg.),
Light scattering in solids III. Recent Results, Band 51 von Topics in applied
physics, Springer-Verlag, Berlin, Heidelberg, New York (1982).
[96] O. Büttner, Zeit- und ortsaufgelöste Untersuchungen mikrowellenangeregter
Spinwellen in dünnen magnetischen Schichten, Dissertation, Fachbereich Physik, Universität Kaiserslautern (1999).
Literaturverzeichnis
115
[97] K. A. Jones, Optoelektronik, Wiley-VCH, Weinheim, New York, Basel, Cambridge (1992).
[98] E. Hecht, Optik, Oldenbourg, München, Wien, vierte Auflage (2005).
[99] J. R. Sandercock, A high resolution, high contrast interferometer, and its application to Brillouin scattering from magnetic materials, in M. Balkanski (Hrsg.),
Proceedings of the 3rd International Conference on Light Scattering in Solids,
Campinas, Brazil, 25-30 July 1975, 219, Flammarion Sciences, Paris (1976).
[100] S. M. Lindsay, M. W. Anderson, J. R. Sandercock, Construction and alignment of a high performance multipass vernier tandem Fabry-Perot interferometer, Rev. Sci. Instrum. 52, 1478 (1981).
[101] R. Mock, B. Hillebrands, R. Sandercock, Construction and alignment of
a high performance multipass vernier tandem Fabry-Perot interferometer, J.
Phys. E Sci. Instrum. 20, 656 (1987).
[102] B. Hillebrands, Progress in multipass tandem Fabry-Perot interferometry: I.
A fully automated, easy to use, self-aligning spectrometer with increased stability and flexibility, Rev. Sci. Instrum. 70, 1589 (1998).
[103] H. Schultheiß, Brillouin–Lichtstreumikroskopie an magnetischen Mikrostrukturen, Diplomarbeit, Fachbereich Physik, TU Kaiserslautern (2005).
[104] O. Büttner, M. Bauer, S. O. Demokritov, B. Hillebrands, Y. S. Kivshar, V. Grimalski, Y. Rapport, A. N. Slavin, Linear and nonlinear diffraction of dipolar
spin waves in yttrium iron garnet films observed by space- and time-resolved
Brillouin light scattering, Phys. Rev. B 61, 11576 (2000).
[105] S. Caponi, M. Dionigi, D. Fioretto, M. Mattarelli, L. Palmieri, G. Socino,
Electro-optic modulator for high resolution Brillouin scattering measurements,
Rev. Sci. Instrum. 72, 198 (2001).
[106] S. O. Demokritov, A. A. Serga, A. André, V. E. Demidov, M. P. Kostylev,
B. Hillebrands, A. N. Slavin, Tunnelling of Dipolar Spin Waves through a Region of Inhomogeneous Magnetic Field, Phys. Rev. Lett. 93, 047201 (2004).
[107] G. A. Melkov, V. I. Vasyuchka, V. V. Lazovskiy, V. S. Tiberkevich, A. N. Slavin, Wave front reversal with frequency conversion in a nonreciprocal medium,
Appl. Phys. Lett. 89, 252510 (2006).
[108] G. A. Melkov, V. I. Vasyuchka, A. V. Chumak, V. S. Tiberkevich, A. N. Slavin,
Wave front reversal of nonreciprocal surface dipolar spin waves, J. Appl. Phys.
99, 08P513 (2006).
116
Literaturverzeichnis
[109] A. N. Slavin, O. Büttner, M. Bauer, S. O. Demokritov, B. Hillebrands, M. P.
Kostylev, B. A. Kalinikos, V. V. Grimalsky, Y. Rapoport, Collision properties
of quasi-one-dimensional spin wave solitons and two-dimensional spin wave
bullets, Chaos 13, 693 (2003).
[110] T. D. Poston, D. D. Stancil, A new microwave ring resonator using guided
magnetostatic surface waves, J. Appl. Phys. 55, 2521 (1984).
[111] M. Kostylev, V. E. Demidov, U.-H. Hansen, S. O. Demokritov, Nonlinear
mode conversion in monodomain magnetic squares, Phys. Rev. B 76, 224414
(2007).
[112] K. Y. Guslienko, S. O. Demokritov, B. Hillebrands, A. N. Slavin, Effective dipolar boundary conditions for dynamic magnetization in thin magnetic stripes,
Phys. Rev. B 66, 132402 (2002).
[113] M. P. Kostylev, G. Gubbiotti, J.-G. Hu, G. Carlotti, T. Ono, R. L. Stamps,
Dipole-exchange propagating spin-wave modes in metallic ferromagnetic stripes, Phys. Rev. B 76, 054422 (2007).
[114] M. Abramowitz, I. A. Stegun (Hrsg.), Handbook of Mathematical Functions,
Dover Puplications, Inc., New York (1965).
[115] V. F. Dmitriev, B. A. Kalinikos, Excitation of propagating magnetization waves by microstrip antennas, Sov. Phys. J. 31, 875 (1988).
[116] V. T. Synogach, Y. K. Fetisov, C. Mathieu, C. E. Patton, Ultrashort Microwave
Pulses Generated Due to Three Magnon Interactions, Phys. Rev. Lett. 85, 2184
(2000).
[117] J. Durnin, Exact solutions for nondiffracting beams. I. The scalar theory, J.
Opt. Soc. Am. A 4, 651 (1987).
[118] J. Durnin, J. J. Miceli, J. H. Eberly, Diffraction-free beams, Phys. Rev. Lett.
58, 1499 (1987).
[119] R. Y. Chiao, E. Garmire, C. H. Townes, Self-Trapping of Optical Beams, Phys.
Rev. Lett. 13, 479 (1964).
[120] O. Büttner, M. Bauer, S. O. Demokritov, B. Hillebrands, Y. S. Kivshar, V. Grimalsky, Y. Rapoport, M. P. Kostylev, B. A. Kalinikos, A. N. Slavin, Spatial and
spatiotemporal self-focusing of spin waves in garnet films observed by spaceand time-resolved Brillouin light scattering, J. Appl. Phys. 87, 5088 (2000).
Literaturverzeichnis
117
[121] B. Taylor, H. J. Maris, C. Elbaum, Phonon Focusing in Solids, Phys. Rev.
Lett. 23, 416 (1969).
[122] B. A. Kalinikos, A. N. Slavin, Theory of dipol-exchange spin wave spectrum
for ferromagnetic films with mixed exchange boundary conditions, J. Phys. C
Solid State 19, 7013 (1986).
[123] D. A. Allwood, G. Xiong, C. C. Faulkner, D. Atkinson, D. Petit, R. P. Cowburn, Magnetic Domain-Wall Logic, Science 309, 1688 (2005).
[124] D. A. Allwood, G. Xiong, R. P. Cowburn, Writing and erasing data in magnetic domain wall logic systems, J. Appl. Phys. 100, 123908 (2006).
[125] R. P. Cowburn, M. E. Welland, Room Temperature Magnetic Quantum Cellular Automata, Science 287, 1466 (2000).
[126] A. Imre, G. Csaba, L. Ji, A. Orlov, G. H. Bernstein, W. Porod, Majority Logic
Gate for Magnetic Quantum-Dot Cellular Automata, Science 311, 205 (2006).
[127] J. William C. Black, B. Das, Programmable logic using giantmagnetoresistance and spin-dependent tunneling devices (invited), J. Appl.
Phys. 87, 6674 (2000).
[128] R. Richter, H. Boeve, L. Bär, J. Bangert, U. K. Klostermann, J. Wecker,
G. Reiss, Field programmable spin-logic based on magnetic tunnelling elements, J. Magn. Magn. Mater. 240, 127 (2002).
[129] R. Richter, L. Bär, J. Wecker, G. Reiss, Nonvolatile field programmable spinlogic for reconfigurable computing, Appl. Phys. Lett. 80, 1291 (2002).
[130] A. Ney, C. Pampuch, R. Koch, K. H. Ploog, Programmable computing with a
single magnetoresistive element, Nature 425, 485 (2003).
[131] G. Reiss, D. Meyners, Reliability of field programmable magnetic logic gate
arrays, Appl. Phys. Lett. 88, 043505 (2006).
[132] C. Bayer, persönliche Mitteilung.
[133] T. Neumann, A. A. Serga, B. Hillebrands, M. P. Kostylev, Frequencydependent reflection of spin waves from a magnetic inhomogeneity induced by
a surface direct current, Appl. Phys. Lett. 94, 042503 (2009).
[134] A. Yariv, Optical Electronics in Modern Communications, Oxford University
Press, New York, fünfte Auflage (1997).
118
Literaturverzeichnis
[135] I. N. Sneddon, Special functions of mathematical physics and chemistry,
Longman, London, New York, dritte Auflage (1980).
Lebenslauf
Thomas Schneider
Persönliche Daten:
Geburtsdatum:
Geburtsort:
Staatsangehörigkeit:
Familienstand:
03.06.1980
Koblenz
deutsch
ledig
Schulbildung:
1986 - 1990
1990 - 1999
21.06.1999
Grundschule Arzheim
Bischöfliches Cusanus Gymnasium Koblenz
Abschluss allgemeine Hochschulreife
Zivildienst:
1999 - 2000
Brüderkrankenhaus St. Josef, Koblenz
Hochschulausbildung:
2000 - 2005
07.11.2002
21.10.2005
Seit 2005
2005 - 2008
Physik-Studium, Technische Universität Kaiserslautern
Vordiplom in Physik mit Nebenfach Informatik
Diplom in Physik mit Nebenfach Informatik , Diplomarbeitsthema:
Bestimmung und Beeinflussung der Phaseneigenschaften
von Spinwellen in Yttrium–Eisen–Granat–Wellenleiterstrukturen
Promotion an der Technische Universität Kaiserslautern in der
Arbeitsgruppe von Prof. Dr. B. Hillebrands
Stipendiat des Graduiertenkollegs
Nichtlineare Optik und Ultrakurzzeitphysik“
”
Danksagung
An dieser Stelle sei all denen mein persönlicher Dank ausgesprochen, die auf verschiedenste Weise zum Gelingen dieser Arbeit beigetragen haben:
Prof. Dr. Burkard Hillebrands für die interessante Aufgabenstellung, dass in mich
gesetzte Vertrauen und die vielen Freiheiten bei der Bearbeitung des Themas.
Prof. Dr. Michael Fleischhauer für die Übernahme des Zweitgutachtens.
Dr. Oleksandr A. Serha für die hervorragende Betreuung, die vielen hilfreichen und
interessanten (wenn auch nicht immer fachbezogenen) Diskussionen und für drei außergewöhnlich unterhaltsame Jahre im selben Büro.
Dr. Mikhail P. Kostylev für die Hilfe bei allen theoretischen Problemen, die stetige
Diskussionsbereitschaft und viele gute Ideen.
Prof. Dr. Andrei N. Slavin und Dr. Vasil S. Tyberkevich für die theoretische Beschreibung der Kaustikstrahlen.
Dr. Matthieu Bailleul für die ausgesprochen hilfreiche Diskussion über die Anregung von Surface Wellen.
Dr. Britta Leven für die gute Zusammenarbeit und die Unterstützung.
Dr. Andrii Chumak, Christian Sandweg, Dr. Sandra Wolff und dem gesamten Nano+Bio Center für ihre unendlichen und schließlich erfolgreichen Mühen ein Strukturierungsverfahren für YIG zu entwickeln.
Timo Neumann für die Hilfe mit Matlab und dem alltäglichen Kleinkram im Labor.
Volker Kegel, Sebastian Schäfer und Dr. Vitaliy Vasyuchka für die gute Zusammenarbeit im Labor.
Sebastian Hermsdörfer für die Hilfe mit dem alltäglichen Kleinkram außerhalb des
Labors.
Dr. Andreas Beck für die Hilfe bei allen Problemen mit LATEX.
Sibylle Müller, Alexander Paul, Bernd Pfaff und Dieter Weller für die Hilfe bei allen
technischen und organisatorischen Problemen.
Allen aktuellen und ehemaligen Mitgliedern der AG Hillebrands für die gute Zusammenarbeit und das angenehme Arbeitsklima.
Dem Graduiertenkolleg 792 “Nichtlineare Optik und Ultrakurzzeitphysik” für die
finanzielle Unterstützung.
Eva-Maria Graefe, Christian Ringl und Thorsten Wagner, die dafür gesorgt haben,
dass meine Zeit an der Uni nicht nur aus Physik bestand. Die letzten Jahre wären
ohne euch wahrscheinlich um einiges produktiver gewesen, allerdings auch deutlich
langweiliger. . .
Meinen “Lektoren” Sebastian Hermsdörfer, Timo Neumann und Thorsten Wagner
denen ich zwar schon an anderer Stelle gedankt habe, die aber für die Sisyphus–
Aufgabe meine Rechtschreibung zu korrigieren eine zweite Erwähnung verdient haben.
Meinen Eltern für ihre Unterstützung und Hilfe wann immer ich sie gebraucht habe.