Also ist 1 sec ) + sec . Da wir sow ohl sec ) = 0 m als auch die W erte

( + 1 sec)
( ) + ( ) 1 sec .
(0 sec) 1 sec + (1 sec) 1 sec + (2 sec) 1 sec
2
t
3
4
5
00
2
4
6
8
10
12
14
2
t
3
4
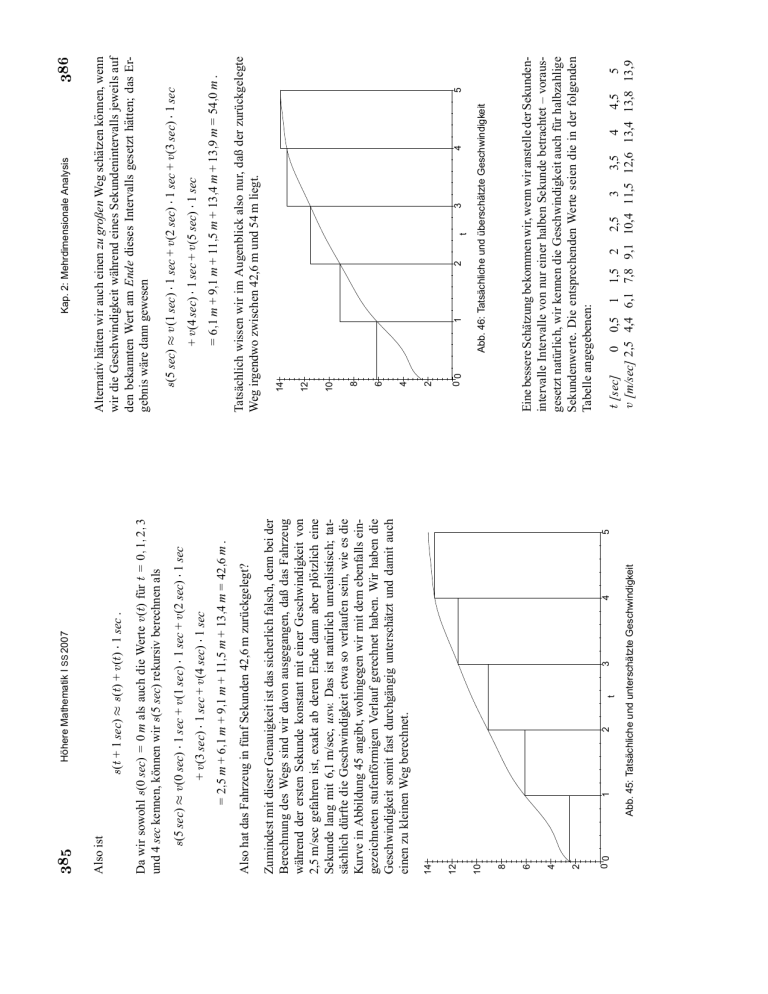
Abb. 46: Tatsächliche und überschätzte Geschwindigkeit
1
5
[sec]
0 0,5 1 1,5 2 2,5
3
3,5
4
4,5
5
[m/sec] 2,5 4,4 6,1 7,8 9,1 10,4 11,5 12,6 13,4 13,8 13,9
Eine bessere Schätzung bekommen wir, wenn wir anstelle der Sekundenintervalle Intervalle von nur einer halben Sekunde betrachtet – vorausgesetzt natürlich, wir kennen die Geschwindigkeit auch für halbzahlige
Sekundenwerte. Die entsprechenden Werte seien die in der folgenden
Tabelle angegebenen:
Abb. 45: Tatsächliche und unterschätzte Geschwindigkeit
1
00
2
Tatsächlich wissen wir im Augenblick also nur, daß der zurückgelegte
Weg irgendwo zwischen 42,6 m und 54 m liegt.
4
6
8
10
12
= 6 1 m + 9 1 m + 11 5 m + 13 4 m + 13 9 m = 54 0 m .
14
Zumindest mit dieser Genauigkeit ist das sicherlich falsch, denn bei der
Berechnung des Wegs sind wir davon ausgegangen, daß das Fahrzeug
während der ersten Sekunde konstant mit einer Geschwindigkeit von
2,5 m/sec gefahren ist, exakt ab deren Ende dann aber plötzlich eine
Sekunde lang mit 6,1 m/sec, usw. Das ist natürlich unrealistisch; tatsächlich dürfte die Geschwindigkeit etwa so verlaufen sein, wie es die
Kurve in Abbildung 45 angibt, wohingegen wir mit dem ebenfalls eingezeichneten stufenförmigen Verlauf gerechnet haben. Wir haben die
Geschwindigkeit somit fast durchgängig unterschätzt und damit auch
einen zu kleinen Weg berechnet.
+ (4 sec) 1 sec + (5 sec) 1 sec
Also hat das Fahrzeug in fünf Sekunden 42,6 m zurückgelegt?
(1 sec) 1 sec + (2 sec) 1 sec + (3 sec) 1 sec
= 2 5 m + 6 1 m + 9 1 m + 11 5 m + 13 4 m = 42 6 m .
(5 sec)
+ (3 sec) 1 sec + (4 sec) 1 sec
Kap. 2: Mehrdimensionale Analysis
Alternativ hätten wir auch einen zu großen Weg schätzen können, wenn
wir die Geschwindigkeit während eines Sekundenintervalls jeweils auf
den bekannten Wert am Ende dieses Intervalls gesetzt hätten; das Ergebnis wäre dann gewesen
(5 sec)
Da wir sowohl (0 sec) = 0 m als auch die Werte ( ) für = 0 1 2 3
und 4 sec kennen, können wir (5 sec) rekursiv berechnen als
Also ist
Höhere Mathematik I SS 2007
9
sec
1
sec = 51 3 m ,
2
50
=0
10
sec
sec
1
sec
10
1
sec
10
=1
10
49 16 m .
48 02 m
Gehen wir von den Zehntelsekunden zu den Hundertsteln, sind die
Rechtecke zumindest visuell in Abbildung 49 nicht mehr voneinander
und von der Fläche unter der Kurve zu unterscheiden: Daß man hier keine durchweg schwarze Fläche sieht, liegt ausschließlich an sogenannten
alias-Effekten, d.h. Diskretisierungsfehlern der Rastergraphik.
Wie Abbildung 48 zeigt, unterscheiden sich nun die Rechtecke der
unteren Abschätzung nur noch wenig von denen der oberen, und die
Fläche unter der Geschwindigkeitskurve liegt schon recht nahe bei der
Fläche der Rechtecke aus jeder der beiden Abschätzungen.
und die obere auf
49
Beide Werte wie auch ihre Differenz lassen sich anhand von Abbildung 47 leicht geometrisch veranschaulichen: Die unterschätzte Geschwindigkeit ist die Fläche der Rechtecke unterhalb der unteren Treppenfunktion, die überschätzte entsprechend die Fläche der Rechtecke
unterhalb der oberen Treppenfunktion, wobei die Basis der Rechtecke
jeweils auf der Zeitachse liegt. Die Differenz ist somit gleich der Fläche
der Differenzrechtecke.
5
Abb. 47: Abtastung in Intervallen von einer halben Sekunde
t
4
00
2
4
49 99 m .
6
1
sec
4
47 14 m
Mit zehn Geschwindigkeitswerten pro Sekunde verbessert sich die untere Schranke auf
sec
1
sec
4
8
3
=1
12
4
sec
10
14
20
und als obere Schranke
2
=0
4
1
19
Wenn wir die Geschwindigkeit viermal pro Sekunde bestimmen und den
zurückgelegten Weg damit schätzen, erhalten wir als untere Schranke
die Unsicherheit hat sich also etwa halbiert. Abbildung 47 zeigt den
Verlauf von unterschätzter, tatsächlicher und überschätzter Geschwindigkeit für die Halbsekundenintervalle.
2
=1
1
sec = 45 6 m ,
2
10
und die überschätzte“ ist
”
sec
=0
2
Diese können wir durch weitere Verfeinerung der Abtastung verkleinern. Dazu nehmen wir an, die eingezeichnete Kurve (die tatsächlich
einfach eine notdürftig angepaßte Polynomfunktion darstellt) gebe den
tatsächlichen Geschwindigkeitsverlauf wieder, und lassen den Computer rechnen:
Kap. 2: Mehrdimensionale Analysis
Jetzt ist die unterschätzte“ Wegstrecke
”
Höhere Mathematik I SS 2007
2
t
3
4
5
48 607 m
1
sec
10000
48 6017 m ;
48 6006 m
5
=0
1
1
und
=1
5
1
2) Integration als Flächenbestimmung: Die Abbildungen 48 und vor
allem 49 zeigen, daß die immer feiner werdenden Rechtecke, die wir für
die obigen Abschätzungen wählten, die Fläche unter der Kurve = ( )
immer besser annähern. Wenn wir die Einheiten vergessen und wie
auch als Längen ansehen, können wir die oben betrachteten Ausdrücke
=0
das Fahrzeug legte in fünf Sekunden also 48 m und 60,1 cm zurück.
100
48 54 m
10000
1
sec
10000
1
sec
100
sec
=1
sec
sec
50000
=0
10000
499
1
sec
1000
Rechnerisch gibt es noch einen kleinen Unterschied im Dezimeterbereich:
sec
Abb. 49: Abtastung in Intervallen von einer Hundertstelsekunde
1
und
49999
00
2
4
=1
1000
Um die eingangs gestellte Frage nach dem zurückgelegten Weg millimetergenau beantworten zu können (sofern man diese Genauigkeit wirklich
als sinnvoll betrachtet), muß die Geschwindigkeitskurve 10 000 Mal pro
Sekunde abgetastet werden, und wir erhalten die Schranken
für die obere.
5000
für die untere Schranke und
6
8
5
10
4
12
t
3
14
2
48 66 m .
Abb. 48: Abtastung in Intervallen von einer Zehntelsekunde
1
00
2
4
1
sec
100
6
Bei einer nochmaligen Verzehnfachung der Intervallanzahl ist natürlich
graphisch nichts neues mehr zu sehen; die Schätzwerte verbessern sich
auf
4999
1
sec
sec 48 595 m
1000
1000
=0
100
=1
sec
8
500
10
und
Kap. 2: Mehrdimensionale Analysis
12
14
Höhere Mathematik I SS 2007
Genau genommen handelt es sich hier allerdings nicht um die Berechnung dieser Fläche, sondern um die Definition des Flächeninhalts, denn
es gibt schließlich a priori keinen Begriff des Flächeninhalts einer
krummlinig begrenzten Fläche. Die hier gewählte Definition über eine Ausschöpfung mit immer feiner werdenden Rechtecken ist zwar sehr
natürlich, aber nicht zwangsläufig. Sie ist übrigens weit älter als jeder
Begriff eines Integrals oder auch nur Grenzwerts: Bereits vor über zwei
Jahrtausenden, um etwa 370 vor Christus, definierte der griechische Mathematiker EUDOXOS VON CNIDOS (ca. 408–ca. 355), ein Schüler und
späterer Konkurrent PLATOS, Flächeninhalte auf diese Weise; später hat
ARCHIMEDES VON SYRAKUS (287–212) diese Methode perfektioniert
und angewandt auf Kreise und Parabeln; insbesondere berechnete er
22 7 für , in Dezimalzahlen
damit seine Abschätzung 223 71
ausgedrückt 3 1408
3 1429, wobei diese Abschätzung allerdings nicht auf Rechtecken beruht, sondern auf der Konstruktion des
regelmäßigen 96-Ecks.
also auch als Näherungswerte für die Fläche unter der Kurve ansehen
und den Flächeninhalt als ihren gemeinsamen Grenzwert für immer
größer werdendes berechnen.
Höhere Mathematik I SS 2007
5
und
1
5
5
=1
sec
Abstrahieren wir vom Beispiel der Wegberechnung anhand einer Geschwindigkeitskurve und betrachten wir das allgemeine Problem, zu
zu
einer gegebenen reellwertigen Funktion eine neue Funktion
finden derart, daß ( ) = ( ) ist.
b) Integration elementarer Funktionen
Trotzdem ist die Interpretation eines Integrals als Durchschnitt gelegentlich von unabhängigem Interesse, da vor allem bei Anwendungen in der
Quantenphysik oft zwar Durchschnitte existieren, aber keine Zähler“
”
und Nenner“, als deren Quotienten man sie interpretieren könnte.
”
1
entsprechen bis auf einen Faktor von 5 sec
genau denen aus Teil a),
wo wir den Weg abgeschätzt haben – wie es ja auch in der Tat der
Fall sein muß: Die Durchschnittsgeschwindigkeit ist schließlich nichts
anderes als der zurückgelegte Weg dividiert durch die zugrundeliegende
Zeitspanne von fünf Sekunden.
sec
=0
1
3) Integration als Durchschnittsbestimmung: Kehren wir wieder zurück zum Eingangsbeispiel eines sich beschleunigenden Fahrzeugs, und
fragen wir uns, wie hoch die Durchschnittsgeschwindigkeit war. Bei
endlich vielen Werten ist der Durchschnitt natürlich einfach das arithmetische Mittel, also z.B.
1
(0 sec) + (1 sec) + (2 sec) + (3 sec) + (4 sec)
5
1
=
42 6 m sec = 8 52 m sec ,
5
wenn wir die Geschwindigkeiten vom Anfang jedes Sekundenintervalls
nehmen, und
1
(1 sec) + (2 sec) + (3 sec) + (4 sec) + (5 sec)
5
1
=
54 0 m sec = 10 8 m sec ,
5
1
5
Natürlich läßt sich auch hier die Abtastung immer weiter verfeinern; die
entstehenden Ausdrücke
wenn wir die vom Ende nehmen.
Kap. 2: Mehrdimensionale Analysis
Da jede konstante Funktion die Ableitung Null hat, ist mit für jede
reelle Zahl auch + eine solche Funktion; um ein konkretes
hinzuschreiben, müssen wir also einen Funktionswert von festlegen;
der Einfachheit halber sei dies, in Analogie zum obigen Beispiel, der
Wert (0) = 0.
Damit übernimmt die Rolle der Geschwindigkeit , dem Weg entspricht die Funktion , die Variable ist nun anstelle der Zeit , und da
uns an einer beliebigen Stelle interessiert, nicht nur wie im obigen
Beispiel an der Stelle 5, empfiehlt es sich, jetzt als Gesamtzahl der Intervalle zu nehmen, nicht wie oben als Anzahl der Intervalle pro Einheit
, und die
(Sekunde). Die Länge eines jeden Intervalls wird dann zu
1
,
#
!"
2
!"
.
!"
!"
$
'
lim
=
6
3
$
(
!"
2
2=
(2
.
1)
, zumindest in
3
3
1)(
6 3
$
$
2) Die Exponentialfunktion: Versuchen wir dasselbe nochmal für die
Funktion ( ) = . Hier führt ( ) (wieder mit der Festlegung (0) = 0)
#
= 1 steht links und rechts Null, die Formel ist also korrekt.
Für
$
eine Formel, die dann nachträglich leicht durch vollständige Induktion
bewiesen werden kann:
3
Diese Funktion hat tatsächlich die Ableitung ( ) =
diesem Beispiel funktioniert also die Definition ( ).
1
=
,
1)
$
=0
$
2
1)(
6
1
1)
(2
1)(
6
!"
lim
3
1
(2
lim
6
3
!"
=
1)
$
2
1)(2
6
1
=
3
( )=
Wie man in seiner Formelsammlung nachschlägt oder sich von seinem
Computeralgebrasystem sagen läßt, ist
=0
3
1
1
Nach dem Prinzip der vollständigen Induktion ist diese damit für alle
Werte von bewiesen; wir können sie in obige Rechnung einsetzen und
erhalten
$
lim
=0
,
(
1)
2
1)
6)
$
3
= lim
1)
)=
7 +6+6
2) + 6(
+(
=
=0
def
selbst.
$
( ) = lim
d.h. die Formel für
$
2
2
$
1)(
6
1
1
$
: Hier erhalten wir
$
1) Die Funktion ( ) =
2
$
(2
1
(2
=
$
$
6
(2
1
$
3)(
2)
2)
$
=
$
(2
$
6
6
1
3)(
$
=
=
6
6
3)(
2
=0
$
1)(2
1)(2
$
=0
( )
(
(
1 anstelle von , d.h. wir
$
in der Hoffnung, daß dieser Grenzwert existiert und mit dem anderen
übereinstimmt – zumindest in hinreichend vielen interessanten Fällen.
Bevor wir uns im nächsten Paragraphen dieser Frage zuwenden, wollen
wir hier zunächst etwas mit dieser vorläufigen Definition spielen und
sehen, was sie bei einfachen Funktionen liefert.
def
=
( ) = lim
2
1
=0
=
$
1
ist. Dann folgt
2
$
Wir definieren daher
der ge-
2
=1
&
deren gemeinsamer Grenzwert für immer größer werdendes
suchte Wert ( ) sein sollte.
und
$
=0
Angenommen, wir hätten sie bewiesen für
1
wüßten, daß für ein spezielles
Kap. 2: Mehrdimensionale Analysis
Analoga zu obigen Summen sind die Ausdrücke
Höhere Mathematik I SS 2007
%
#
*
)
auf den Ansatz
def
*
!"
(
'
!"
)
!"
)
,
+
+
+
+
+
+
$
+
+
+
+
$
+
+
-
$
.
+
+
$
+
+
$
+
.
1
*
*
'
(
)
*
$
)
+
)
$
)
*
)
!"
$
!"
*
$
*
)
$
12
)
!"
$
1
Im Grenzwert ganz rechts gehen für
leider sowohl der Zähler
als auch der Nenner gegen Null, wir müssen also die Regel von DE
L’HOSPITAL anwenden. Diese gilt zwar nur für Grenzwerte von Werten
stetiger Funktionen, während wir hier den Grenzwert einer diskreten
ist.
1,
def
def
( ) = lim
(0) = 0 ist wieder
.
9
8
.
=0
1
1 für
0 für
.
!"
Dabei ist die Zahl
für = 0 rational, da Null; für = 0 ist sie
genau dann rational, wenn auch rational ist. In diesem Fall ist also
Mit
( )=
1
=
3) Die Dirichletsche Sprungfunktion: Bevor wir zu übermütig werden,
möchte ich als letztes Beispiel noch eine Funktion betrachten, die sich
im Gegensatz zu Quadrat und Exponentialfunktion alles andere als gut
verhält, die DIRICHLETsche Sprungfunktion
7
.
1
1
eine Funktion, deren Ableitung in der Tat
)
1
/ 0
lim
.
8
) lim
+
9
= (1
1
+
=
4
= 1; wir können die
$
=
!"
$
Da uns nur der Fall = 0 interessiert, ist
Formel also anwenden und erhalten
4
1
4
)
)
1
+
( ) führt dies auf
.
4
lim
( ) = (1
1
2
4
( )=
=
)
1
2
=0
.
4
!"
*
*
1
1
$
$
)$
=
4
)
1
!"
)
4
dividieren und erhalten die Formel
*
6
4
*
Eingesetzt in den Ansatz für
$
1
$
= lim
(1
4
.
1
6
4
*
= 1 können wir durch 1
+
4
)
=1
1
*
=0
+
= lim
)
+
1
!" $
4
Für
)
1
+
3
6
+
6
2
= lim
5
(1
1
5
*
=0
lim
Nach DE L’HOSPITAL ist
=1 2 3
5
+
1
)
+
4
*
=
+
für
1
3
der Grenzwert
=0
+
*
2
$
+
)
=1+
1
gegen eben diesen Grenzwert.
*
1
1
4
Die Summe ganz rechts ist eine geometrische Reihe und kann leicht
ausgerechnet werden: Setzen wir zur Abkürzung =
, so ist
$
1
existiert, konvergiert natürlich auch die Folge der Zahlen
4
.
!"
=0
4
)
1
lim
*
lim
=0
1
Folge suchen, aber wenn für eine reelle Variable
Kap. 2: Mehrdimensionale Analysis
3
=
= lim
1
*
=0
1
( ) = lim
1
Höhere Mathematik I SS 2007
=
.
!"
!"
( ) = lim
!"
7
,
8
8
9
Auch unter dem Gesichtspunkt der Interpretation von ( ) als Fläche
unterhalb der Kurve = ( ) ist das Ergebnis unbefriedigend, denn
da ( )
0 für alle , sollte ( ) eine monoton wachsende (oder
zumindest nicht fallende) Funktion von sein, wohingegen das gerade
berechnete bei jeder rationalen Zahl auf Null zurückfällt.
eine offensichtlich nicht differenzierbare Funktion, und wenn
( )
nicht einmal existiert, kann es natürlich auch nicht gleich ( ) sein.
für
für
0
9
( )=
= 0.
Also ist
für rationales . Für irrationales dagegen sind alle
außer der
Null irrational, also ist (
) = 0 für alle = 0. Damit bleibt von der
Summe nur der erste Summand stehen, d.h.
= lim
=0
1
( ) = lim
) = 1 für alle , d.h.
:
;
Der Ansatz ( ) hat also auch seine Tücken, und es wird Zeit, diese
heuristische Definition durch eine bessere zu ersetzen.
#
Tatsächlich ist der Ansatz ( ) nicht so schlecht: Für die beiden gutartigen Funktionen und für das Eingangsbeispiel der Streckenbestimmung
führte er schließlich zu vernünftigen Ergebnissen, und wie wir bald sehen werden, kann man Integrale über stetige Funktionen immer nach
diesem Ansatz bestimmen; zumindest als Veranschaulichung des Integralbegriffs sollte man ihn daher durchaus im Hinterkopf behalten.
Problematisch wird er erst bei schlechten“ Funktionen wie der im letz”
ten Beispiel.
c) Definition des Riemann-Integrals
#
ist für
;
0 monoton wachsend, ( ) =
sogar für
*
Auch ( ) =
2
2) Wo sollte der bisherige Ansatz modifiziert werden?: Ein Punkt, bei
dem der bisherige Ansatz nur aufgrund der Einfachheit der betrachteten Beispiele so erfolgreich war, ist die Abschätzung des Grenzwerts
durch die endlichen Approximationen. Beim Beispiel der Geschwindigkeit eines beschleunigenden Fahrzeugs war das problemlos, denn die
Geschwindigkeit war eine monoton wachsende Funktion, die für jedes
Teilintervall am linken Ende ihr Minimum und am rechten ihr Maximum
annimmt.
Obwohl wir im folgenden fast jeden der wichtigeren Sätze aus der
Analysis I noch einmal in die Erinnerung zurückrufen und anwenden
müssen, ist die nun folgende Konstruktion also kein Luxus, sondern
zumindest langfristig notwendig auch für praktische Anwendungen.
Wirklich kompliziert wird die Situation dagegen beispielsweise bei der
mathematischen Modellierung des Rauschens in einer elektronischen
Schaltung: Hier liegt eine noch einmal deutlich schwierigere Situation
vor als im obigen Beispiel, und in der Tat wird auch der in diesem
Paragraphen definierte Integralbegriff nicht ausreichen, um mit diesem
Problem fertig zu werden. Er ist aber eine unabdingbare Voraussetzung,
um die dazu bentigten Techniken zu verstehen.
Die DIRICHLETsche Sprungfunktion ist ein rein theoretisch konstruiertes
Gegenbeispiel, das wohl keinerlei praktische Anwendung haben dürfte.
Eine ihrer charakteristischen Eigenschaften taucht allerdings auch bei
praktisch relevanten Funktionen auf: Auch ein periodisch wiederholter
Rechteckimpuls hat abzählbar unendlich viele Sprungstellen, und zumindest als Idealisierung eines realen Signals spielt diese Funktion eine
Rolle – sie ist allerdings erheblich harmloser als DIRICHLETS Beispiel,
da die Menge ihrer Sprungstellen diskret ist.
1) Warum lohnt sich ein allgemeinerer Ansatz?: Dies legt natürlich die
Frage nahe, ob man solche schlechten“ Funktionen für Anwendungen
”
wirklich braucht, und wenn ja, ob man sie so sehr braucht, daß sich der
erhebliche technische Aufwand, den wir in diesem Paragraphen treiben
müssen, lohnt.
Kap. 2: Mehrdimensionale Analysis
(
Höhere Mathematik I SS 2007
)
<
8
, so daß wir auch hier leicht untere und obere Schranken für
alle
( ) berechnen können.
Höhere Mathematik I SS 2007
$
1
$
1.5
t
2
2.5
3
$
$
$
$
Wenn man ein (jedem Wissenschaftler zu empfehlendes) gesundes Mißtrauen gegen Computer und Taschenrechner mitbringt, könnte man versucht sein, den Wert 1,954 als eine Taschenrechnerzwei“ zu interpre”
tieren; da aber die Sinuswerte an den Stellen 0 6 3 2 43 56 und 1
wohlbekannt sind (im Winkelmaß ausgedrückt sind diese Stellen gerade die Vielfachen von 30 ), kann man die Summe der Rechteckflächen
Abb. 50: Sinuslinie mit sechs Rechtecken zum jeweils linken Funktionswert
0.5
$
00
2
2.5
3
exakt berechnen mit dem Ergebnis
Abb. 51: Sinuslinie mit sechs Rechtecken zum jeweils rechten Funktionswert
1.5
t
(2 + 3) ,
6
das schon wegen der Transzendenz von nicht gleich zwei sein kann.
Somit haben wir definitiv keine obere Schranke für den korrekten Wert,
und zumindest a priori haben wir auch keine untere, denn daß die
Summe der Rechteckflächen kleiner ist als die Fläche unter der Kurve
folgte je erst nachträglich durch Vergleich der beiden Werte.
=
=
=
=
+
+2
+(
1)
+
B
A
=
mit
Für eine beliebige Funktion gibt es aber offensichtlich keinen Grund,
warum das Minimum oder Maximum überhaupt an einem Intervallende
angenommen werden sollte; für einen möglichst allgemeinen Integrallbegriff sollte man also auch Punkte im Intervallinnern zur Ermittlung
der Höhe des Rechtecks heranziehen: Anstelle der bislang betrachteten
Unterteilung
Um wirklich eine untere Schranke für die Fläche zu bekommen, müßte
man hier im Beispiel für die ersten drei Rechtecke den Funktionswert am
linken Ende des Teilintervalls nehmen und für die letzten drei den vom
rechten; für eine obere Schranke müßte man genau umgekehrt vorgehen.
0.2
0.4
( 1) = 1 + 1 = 2 .
1
0.6
( 1)
0.5
?
0.8
1
( cos 0) =
00
0.2
0.4
0.6
0.8
cos
Für nichtmonotone Funktionen dagegen ist die Situation völlig anders:
Betrachten wir als Beispiel etwa die Sinuslinie zwischen Null und
mit einer Annäherung der Fläche durch sechs Rechtecke. In den Abbildungen 50 und 51 sind diese Rechtecke eingezeichnet, einmal bezogen
auf den Funktionswert am linken Ende des Teilintervalls und einmal
bezogen auf den am rechten. Wie man sieht, liegen die Rechtecke exakt spiegelsymmetrisch zueinander und haben damit insbesondere die
gleiche Summe der Flächeninhalte, nämlich jeweils ungefähr 1,954. Die
Fläche unter der Sinuslinie zwischen Null und ist allerdings, wie wir
bald sehen werden,
1
Kap. 2: Mehrdimensionale Analysis
%
$
A
=
@
B
A
@
$
@
A
@
A
@
@
=
>
%
1
=
B
3 3 C
8
@
( )
$
3
3
$
3 C
$
C
).
C
+1
C
( )(
1 )(
=0
+ (
1)
2
t
3
4
5
Der Haken bei der Sache ist natürlich, daß wir die geeignet gewählten“
”
Rechtecke nicht kennen: Im obigen Ausdruck ist alles bekannt außer
den Werten , an denen die Funktion ausgewertet wird.
gleich der Fläche der fünf Rechtecke, sondern auch die Fläche eines
jeden Rechtecks gleich der Fläche zwischen Kurve und Grundlinie des
Rechtecks, wir kommen also mit endlich vielen Rechtecken aus und
brauchen nicht einmal einen Grenzwert zu berechnen.
Die Idee zur Definition des RIEMANN-Integrals ist nun, daß man einfach
beliebige zwischen und +1 wählt in der Hoffnung, daß bei immer
kleiner werdendem Abstand zwischen zwei aufeinanderfolgenden
der Grenzwert nicht mehr von der Wahl der abhängt.
Diese Hoffnung hat natürlich nur eine Chance auf Erfüllung, wenn die
Funktion hinreichend stetig ist; ansonsten können sich die Werte von
an zwei beliebig nahe beieinanderliegenden Stellen immer noch beliebig
stark unterscheiden, indem sie beispielsweise wie oben davon abhängen,
ob rational ist oder nicht.
C
:
$
Damit ist also die Fläche unter der Kurve = ( ) exakt gleich der Gesamtfläche endlich vieler geeignet gewählter Rechtecke; Abbildung 52
veranschaulicht dies anhand der ganz zu Beginn betrachteten Geschwindigkeitsfunktion. Hier ist nicht nur die Fläche unter der Kurve exakt
( 0) +
C
2)
1)
$
1
$
1
1 )(
1 )(
$
+ (
+ (
).
=
C
..
.
=
$
C
2)
(
=
+1
1)
C ( ) + ( )(
(
( )= ( )
)=
=
(
( )=
C
Rekursiv folgt, daß
$
=
+1 )
+1
( )
C
C
(
+1 )
wäre, d.h.
(
1
Abb. 52: Die Fläche unter der Kurve ist gleich der Fläche der fünf Rechtecke
00
2
4
6
8
10
12
14
Kap. 2: Mehrdimensionale Analysis
Wir suchen zu einer gegebenen Funktion eine differenzierbare Funktion mit
= . Falls wir annehmen, daß wir diese Funktion schon
hätten, so wäre
= , und nach dem Mittelwertsatz gäbe es in jedem
)
ein
Element , so daß
Intervall (
+1
ist.
C
( )=
( )
3) Anwendung des Mittelwertsatzes: Einen weiteren Grund dafür liefert
der wohl wichtigste Satz aus der Analysis I, der Mittelwertsatz der Differentialrechnung: Ist stetig in einem Intervall [
] und differenzierbar
in (
), so gibt es einen Punkt
(
), so daß
2
1
0
treten.
=
sollte also eine beliebige Unterteilung
Höhere Mathematik I SS 2007
%
4) Gleichmäßige Stetigkeit: Die Stetigkeit allein reicht allerdings immer
noch nicht ganz aus:
%
<
DE
&
G
A
B
8
A
&
F
D
8
, wenn es
Erinnern wir uns: heißt stetig auf einer Teilmenge
zu jedem
0 und zu jedem
( ) ein
0 gibt, so daß gilt: Ist
und
, so folgt, daß ( )
( )
ist.
@
G
F
:
:
:
$
G G $
Wir möchten mehr: Wir wollen, daß sich in jedem Rechteck der Wert
0 ändert, falls nur die Breite des Rechtecks
von ( ) höchstens um
unter einer gewissen Schranke liegt, d.h. wir möchten, daß nicht von
abhängt
&
F
C
Dies führt auf folgende Verschärfung des Stetigkeitsbegriffs:
A
<
<
D
8
:
DE
&
&
F
D
G
G
F
D
:$
-
AIH
G G $
:
.
&
F
A
A
A
$ L
JKJKJKJ
&
A
;
G
&
F
G
F
F
JKJKJKJ
A
L
A
M
JKJKJKJ
A
JKJKJKJ
A
A
M
L
A
N
F
F
M
A
N
N
F
L
F
:$
Aufgrund der Annahme, der Satz sei falsch, können wir ein solches
fixieren und betrachten die speziellen Werte = 1 : Nach dem gerade
1
gesagten gibt es dazu Punkte
[ ], so daß
,
aber ( )
( )
ist.
F
&
:
B
8
:
@
;
G
F
G
:$
A
G G $
:
&
F
F
JKJKJKJ
:
$ J
JKJKJK
-
F
F
Satz von Bolzano-Weierstraß: Jede Folge ( ) von Punkten aus dem
abgeschlossenen Intervall [ ] hat (mindestens) eine konvergente Teilfolge
.
Nun kommt der nichttriviale Teil: Wir benötigen aus der Analysis I den
A
&
A
A
Damit ist die Stetigkeit der Funktion bewiesen. Sie ist aber nicht
gleichmäßig stetig, denn es gibt aber kein von unabhängiges
0 mit
dieser Eigenschaft: Der angegebene Ausdruck für das größtmögliche
geht wegen des Faktors 2 im Zähler für
0 selbst gegen Null, fällt
also unter jede vorgegebene positive Schranke. Abbildung 53 zeigt in
1
.
Abhängigkeit von für den speziellen Wert = 10
:
A
:$
.
@
G
1
8
1
B
Angenommen, wäre nicht gleichmäßig stetig. Dann gäbe es für mindestens ein
0 zu jedem
0 Punkte
[ ], so daß
,
aber ( )
( )
wäre.
G $
G
1+
=01
:
def
und
1
G F
2
Der Beweis ist technisch und indirekt:
=
@
A
Der Ausdruck ganz rechts ist offensichtlich kleiner, wenn im Nenner
das Pluszeichen steht, also gilt: Für gegebenes
0 und
0 gilt für
jede positive reelle Zahl
8
1
2
B
2
)
@
2
<
)
@
(
A
B
(
@
=
1
)
B
]
sei eine stetige Funktion auf dem abgeschlossenen
] mit
. Dann ist auf [ ] gleichmäßig stetig.
B
Satz: : [
Intervall [
<
(
P
=
P
für ( ) = 1
0.8
P
1
0.6
S
1
x
in Abhängigkeit von
0.4
T
In einem abgeschlossenen Intervall sollte so etwas nicht möglich sein,
und in der Tat gilt der (durchaus nichttriviale)
Abb. 53:
0.2
Um zu sehen, daß dies mehr ist als die bloße Stetigkeit, betrachten wir
die Funktion ( ) = 1 . Diese Funktion ist stetig auf der Menge aller
und
0 ist
positiver reeller Zahlen, denn für 0
A
O
.
0
Q
( )
1
R
( )
<
eine
0 ein
sei eine Teilmenge von
und :
Definition:
Funktion. heißt gleichmäßig stetig in , wenn es zu jedem
0 gibt, so daß für alle
gilt:
0.02
0.04
0.06
0.08
0.1
Kap. 2: Mehrdimensionale Analysis
%
Höhere Mathematik I SS 2007
%
B
@
U
1
Insbesondere muß also die hier betrachtete Folge ( ) eine konvergente
Teilfolge
haben; deren Grenzwert sei
[ ].
B
8
@
Y
WV
U
F
X
%
:
V JKJ
:
$
JKJ
U
U
:
U
U
!"
V
U
!"
V
Z
:
:
U
U
F
1
@
C
C
]
( )+
1
@
( )(
C
=0
3
+1
3
1
).
$
@
C 4
1
4
5
=
C
1
C
@
2
1
2
[
C
C
1)
1
C
C
5
5
5
\
1
=
B
<
B
@
B
@
@
B
@
C
( )(
C
=0
1
)=
$
+1
).
) ist
C
(
Definition: Die RIEMANNsche Summe zu einem Paar (
ein mit der Verabredung, daß immer, wenn ein in Zusammenhang mit
einem auftritt, diese Ungleichungen erfüllt sein sollen.
1
C
0
=(
und führen auch hier wieder die Abkürzung
0
C
C
0
C
=
Natürlich kennen wir die Zahlen
nicht – selbst wenn wir wissen,
daß und damit die überhaupt existieren. Deshalb betrachten wir
einfach beliebige Zahlen mit
( )=
2
C
2
1
2
1
2
0
1
C
C
0
0
0
folgt
=
C
C
=
)
Falls die gesuchte differenzierbare Funktion : [ ]
existiert,
sagt uns – wie wir in Teil c) gesehen haben – der Mittelwertsatz der
Differentialrechnung, daß für geeignete Elemente mit
C
1
1
@
@
2
\
C
B
1
C
]
0
=
5
@
C
Wir wählen eine Unterteilung
5
B
<
1
auf einem abgeschlosWir gehen aus von einer Funktion : [ ]
senen Intervall [ ]; gesucht ist eine Funktion : [ ]
, für die
(idealerweise) ( ) = ( ) sein sollte für alle aus dem offenen Intervall ( ).
5
dafür ein und verabreden, daß die immer, wenn von die Rede ist,
die obigen Gleichungen und Ungleichungen erfüllen sollen, daß sie also
] definieren.
tatsächlich eine Unterteilung von [
1
GEORG FRIEDRICH BERNHARD RIEMANNN (1826-1866)
war Sohn eines lutherischen Pastors und schrieb sich
1946 auf Anraten seines Vaters an der Universität
Göttingen für das Studium der Theologie ein. Schon
bald wechselte an die Philosophische Fakultät, um dort
unter anderem bei GAUSS Mathematikvorlesungen zu
hören. Nach Promotion 1851 und Habilitation 1854 erhielt er dort 1857 einen Lehrstuhl. Trotz seines frühen
Todes initiierte er grundlegende auch noch heute fundamentale Entwicklungen in der Geometrie, der Zahlentheorie und über abelsche Funktionen. Seine Vermutung
über die Nullstellen der (heute als RIEMANNsch bezeichneten) -Funktion ist die berühmteste offene Vermutung
der heutigen Mathematik.
1
0
\
5) Definition einer Approximation für das Integral: Nach diesen Vorarbeiten können wir ernsthaft darangehen, das Integral einer Funktion
zu definieren. Es gibt in der Mathematik verschiedene Integralbegriffe;
für uns reicht die Definition des deutschen Mathematikers BERNHARD
RIEMANNN, das inzwischen nach ihm benannte RIEMANN-Integral.
=(
<
Mithin führt die Annahme, sei nicht gleichmäßig stetig, auf einen
Widerspruch, und damit ist der Satz bewiesen.
Andererseits ist aber für jedes nach Konstruktion der Folgen ( )
und ( ) der Abstand zwischen (
) und ( ) größer oder gleich
der festgewählten Zahl , so daß die beiden Folgen unmöglich denselben
Grenzwert haben können.
@
des Intervalls von bis . Da wir im folgenden viel mit dieser Unterteilung rechnen werden, führen wir die Abkürzung
1
ist, muß dann auch die Folge der
gegen
Da
konvergieren, und da nach Voraussetzung eine stetige Funktion ist,
gilt
lim (
) = lim ( ) = ( ) .
Kap. 2: Mehrdimensionale Analysis
%
Höhere Mathematik I SS 2007
\ ^
\ %
\
=
.
_
\
:
:
@
:a`
:a`
:
@
:
_
_
b
b
\
\
_
\
\
;
c
Z
V \
V \
V \
V \
d
d
V V $
U
!"
V
VC
V \
VC
für jedes
[
B
V \
^
!"
V
8
@
V \
@
1)
()
oder heißt, ist auch
oder bezeichnet
ist RIEMANN-integrierbar
( )
Dazu fixieren wir ein beliebig vorgegebenes
[ ] und betrachten
Folgen ( ( ) ) von immer feiner werdenden Unterteilungen des Intervalls [
]; dazu entsprechende Folgen ( ( ) ) von Zwischenwerten und
die Grenzwerte der RIEMANN-Summen ( ( ) ( ) ).
] existiert.
g
@
).
]
C
VC
( )
=
1)(
6
Zum Beweis müssen wir zeigen, daß das RIEMANN-Integral
:[
*fe
h
VC
( )
( )
(
(2
8
V \
^
*fe
1. Schritt: Für eine feste Folge ( ( ) ) von Unterteilungen existiert der
Grenzwert und ist unabhängig von der Wahl der Zwischenwerte ( ) :
@
V \
C
C
= lim
=
Satz: Jede stetige Funktion
auf [ ].
@
B
( )
sei
6) Existenz des Riemann-Integrals für stetige Funktionen: Damit haben wir das RIEMANN-Integral definiert; wir wissen allerdings bisher für
keine einzige Funktion, daß es existiert. In diesem Abschnitt wollen wir
uns überlegen, daß es zumindest für stetige Funktionen immer existiert:
B
C
VC Dieser Grenzwert muß natürlich im allgemeinen nicht existieren, und
wenn er existiert, kann er von der Wahl der Zwischenpunkte ( ) und
von der Wahl einer Folge ( ( ) ) von Unterteilungen abhängen. Wenn er
unabhängig von all diesen Wahlen existiert und immer denselben Wert
hat, bezeichnen wir diesen gemeinsamen Wert als das RIEMANN-Integral
von zwischen und , in Zeichen
g
unabhängig davon, ob die Integrationsvariable mit
wird.
h
).
C
( )
C
@
( )
*fe
g
B
( )
=
3
1
(
=0
2
3
lim
h
<
Zu jeder Unterteilung ( ) wählen wir willkürlich eine (im Sinne obiger
Konvention dazu passende) Folge ( ) von Zwischenpunkten und fragen
nach Existenz und gegebenenfalls Wert des Grenzwerts
b
*fe
g
) = 0.
i
( )
1
k
*fe
( )
+1
=
C 1
2
$
davon unabhängig ist, ob der Summationsindex
=0
1
3
=0
=0
=
i
lim max (
2
$
h
Nun betrachten wir eine Folge ( ( ) ) von Unterteilungen derart, daß
( +1)
stets eine Verfeinerung von ( ) ist und
die maximale Länge der Teilintervalle von ( ) mit wachsendem
gegen Null geht, d.h.
1
k
Dann heißt eine Verfeinerung von , wenn jedes Teilintervall (
+1 )
)
von
liegt;
entsteht
von ganz in einem der Teilintervalle (
+1
also aus , indem einige der Intervalle von noch weiter unterteilt
werden. Insbesondere muß dann
sein.
1
j
1
@
0
C
=
und
@
=
B
1
8
1
0
@
=
B
] existiert, sagen wir,
heißt Integrationsvariable und übernimmt die Rolle des Summationsindex in einer Summe: Genau wie beispielsweise
[
Falls dieses Integral für jedes
RIEMANN-integrierbar auf [ ].
Kap. 2: Mehrdimensionale Analysis
%
Das RIEMANN-Integral soll der Grenzwert einer Folge RIEMANNscher
Summen sein, wobei die Unterteilungen immer feiner werden. Dieses
Feinerwerden“ müssen wir natürlich auch noch erklären: Seien und
”
zwei Unterteilungen des Intervalls [
]; konkret sei
Höhere Mathematik I SS 2007
VC V \
VC
V \
^
!"
V
h
g
V \
V c
%
V V Nach Definition ist
U V \
^
VC U
=0
;
( )
V V $
V V \
VC
V \
^
Vl U
V V $
Vl V
n
VC
V \
^
)
( )
,
( )
V V V V \
V \
V
n
m
VC
V \
^
m
V V
n
n
VC
V \
^
(3)
V (2)
(1)
V b
(3)
(2)
(1)
.
monoton fallend ist, und da stets
V ;
( )
V Genauso folgt, daß die Folge der
( )
( )
ist, folgt weiter, daß
ein Zusammenhang, der in Abbildung 54 noch einmal graphisch dargestellt ist: Die RIEMANNsche Untersumme ist gleich der Fläche der
durchgezogenen Rechtecke, für die Obersumme kommt noch der gestrichelte Anteil dazu, und für die RIEMANNsche Summe ( ( ) ( ) )
muß man bis zu den punktierten Linien gehen. Die Werte ( ) sind auf
( )
VC ( )
V (
)
V b
( )
gilt somit
( )
Vergleichen wir dazu zunächst die Untersummen ( ) und ( +1) : Die Unterteilung ( +1) entsteht aus ( ) dadurch, daß einige der Intervalle weiter unterteilt werden. Ist aber ( ( +1) ( +1+1) ) Teilintervall von ( ( ) ( +1) ),
so kann das Minimum im Teilintervall natürlich nicht kleiner sein als
( )
im größeren Intervall, d.h. ( +1)
. Somit ist die Folge der ( )
monoton wachsend.
V \
^
( )
.
n
V \
Unabhängig von der Wahl der Zwischenwerte
( )
VC
), die RIEMANNsche Obersumme der Unterteilung
V
auch ( ( ) ( ) ) gegen diesen Grenzwert konvergieren, und die Behauptung im ersten Schritt ist bewiesen.
V für (
( )
( )
V \
^
m
=0
( )
+1
(
( )
( )
( )
VC
( )
m
def
2
Wenn wir jetzt noch zeigen können, daß die Folge der ( ) und die
der ( ) beide gegen denselben Grenzwert konvergieren, muß wegen
der Einschließung
VC n
1
1.5
der -Achse durch kleine Kreise gekennzeichnet, ebenso die Punkte
( )
( ( ) ) auf der Kurve.
V
=
x1
V ( )
0.5
Abb. 54: Riemannsche Summen, Obersummen und Untersummen
00
0.2
0.4
0.6
VC für (
); diese bezeichnen wir als RIEMANNsche Untersumme
der Unterteilung ( ) . Entsprechend liefert die Ersetzung durch ( )
eine obere Abschätzung
def
( )
V c
1
( )
=
( )
+1
VC
V c
jeweils durch
( )
VC ( )
V $
, so erhalten wir eine untere
( )
)
( )
+1
.
V ( )
(
m
( )
( )
Vl =0
)
VC ersetzen wir hierin
Abschätzung
)=
VC m
1
( )
(
V c
( )
(
0.8
1
1.2
Kap. 2: Mehrdimensionale Analysis
( )
( )
Vl ( )
Um das einzusehen, betrachten wir für jede Unterteilung ( ) die RIEMANNschen Obersummen und Untersummen: Da nach Voraussetzung
stetig ist, nimmt es in jedem abgeschlossenen Intervall sowohl sein Maximum als auch sein Minimum an; insbesondere werden also im Intervall
[ ( ) ( +1) ] ein Maximum ( ) und ein Minimum ( ) angenommen.
Damit gilt unabhängig von der Wahl des Zwischenwerts ( )
Höhere Mathematik I SS 2007
%
n
m
n
m
n
m
m
m
m
V
m
V VC und
%
V
n
n
V V V
n
n
U Vo
V V $
U m
V V $
n
=
(
V
Vo
V $
Vo
) ist auch unabhängig von der Folge (
@
5
Z
V V $
@
$
Vo
V V $
Vo
V q
V _
V \
V p
V :b
V Vo
( )
):
V V \
&
A
A
&
F
G
C
C
G $
B
@
C
C
8
G
F
G
C
C $
( )
V \
( )
sV
n
V
n
n
V
n
V m
sV
m
Vs m
V V p
V n
V p
Vs ist; da die Folgen ( ( ) ) und ( ( ) ) denselben Grenzwert haben, müssen
auch ( ( ) ) und ( ( ) ) gegen diesen Wert konvergieren und damit auch
( )
Vs ( )
Wie oben seien ( ) und ( ) die RIEMANNsche Unter- und Obersumme
zur Unterteilung ( ) ; entsprechend seien ( ) und ( ) die zur Unterteilung ( ) . Da ( ) eine Verfeinerung von ( ) ist, wissen wir aus dem
ersten Schritt, daß
5
V als
( )
+1 ]
( )
5
( )
( )
V \
r
)
(
V _
Ist dabei für eine Unterteilung ( ) jede der Differenzen ( +1)
( )
( )
(
kleiner als , so ist auch
, denn sowohl
( )
( )
auch
sind Funktionswerte, die irgendwo im Intervall [
angenommen werden.
.
V q
Hier kommt nun die in Abschnitt c) eingeführte gleichmäßige Stetigkeit von zum Tragen: Danach gibt es zu jedem
0 ein
0,
so daß für alle Punkte 1 2
[ ] gilt: Ist 1
,
so
folgt
2
( 1)
( 2)
.
( )
( )
Betrachten wir zwei Folgen ( ( ) ) und ( ( ) ) von Unterteilungen. Für jeden Index können wir zu den Unterteilungen ( ) und ( ) eine gemeinsame Verfeinerung ( ) konstruieren, indem wir einfach die sämtlichen
( )
Zahlen ( ) und ( ) der Größe nach ordnen als 0( ) =
= .
!"
),
=0
)
2. Schritt: lim
V \
^
und das ist eine Nullfolge, falls wir zeigen können, daß die Folge der
eine ist.
(
V ( )
( )
Der zweite ist zum Glück erheblich einfacher:
=
V l $
U ( )
0 )
V l $
(
V $
( )
+1
V ( )
V c
( )
VC
=0
V $
V \
( )
V $
)=
V ( )
V
( )
+1
!"
(
V \
^
( )
V
( )
V
( )
1
VC
1
!"
( )
( )
,
) = lim
( )
VC Da die linke und die rechte Seite obiger Ungleichung nicht von den ( )
abhängen, ist auch lim ( ( ) ( ) ) davon unabhängig, und damit ist der
erste Schritt des Beweises beendet.
V \
^
ist also
V
= max
n
!"
def
V c
).
( )
VC
( )
( )
)
V
( )
V c
)(
$
V ( )
+1
(
V \
^
m
= lim
V ( )
lim
( )
F
Mit
( )
auch die Gleichung
( )
m
(
Vl ( )
)
(
n
=0
1
U
=0
( )
V
=
U =0
( )
Z
( )
+1
&
(
V $
( )
Z
)
V ( )
V l $
( )
+1
A
V
(
V c
!"
( )
Z
V VC
=
Vo
V
n
( )
Z
!"
( )
&
n
n
V
Wie schon erwähnt, folgt daraus aufgrund der Einschließung
V 1
&
.
Vo
1
F
( )
V $
= lim
Z
Dazu betrachten wir die Differenzen
A
( )
&
lim
Z
Nun fehlt nur noch, daß beide denselben Grenzwert haben.
Z
Nun haben wir aber vorausgesetzt, daß die Unterteilungen ( ) immer
0 gibt es in der Tat ein 0 , so daß
feiner werden, d.h. zu jedem
( )
( )
für
alle
und
alle . Somit sind für
0
0 alle
+1
( )
( )
( )
kleiner als , und damit ist auch
für
Differenzen
( )
( )
) als auch ( )
Nullfolgen, d.h.
0 . Also sind sowohl (
V \
Damit ist also die Folge ( ( ) ) monoton wachsend und nach oben beschränkt, während ( ( ) ) monoton fallend und nach unten beschränkt ist.
Nach einem Satz aus der Analysis I (Jede monotone und beschränkte
Folge reeller Zahlen ist konvergent.) folgt daraus die Konvergenz beider
Folgen.
( )
Kap. 2: Mehrdimensionale Analysis
Insbesondere ist also (1) eine obere Schranke für die Folge der
(1)
eine untere Schranke für die Folge der ( ) .
Höhere Mathematik I SS 2007
%
V
n
Vl $
V V F
V c
V \
V l $
A
V c
sV
%
]
@
(2)
3
(2)
5
:
:
:
]
]
B
:
@
5
@
q
q
]
]
B
VC
q
q
VC
q
VC
q
V p
^
q
@
Beweis:
:[
=
VC
V \
^
!"
V
=
1
]
+1 )
= .
@
mit
ist RIEMANN-
@
@
Wiederholt man den Beweis des entsprechenden Satzes für Funktionen, die auf ganz [ ] stetig sind, so funktioniert fast alles problemlos
auch für . Schwierigkeiten gibt es nur mit den Intervallen einer Unterteilung , die einen der Punkte
enthalten. In diesen Intervallen
ist nicht notwendigerweise stetig, so daß die Differenz zwischen dem
Supremum und dem Infimum von dort nicht mit Verkleinerung des
Intervalls gegen Null gehen muß, sondern auch gegen einen von Null
verschiedenen Wert, nämlich die Sprunghöhe“ bei , konvergieren
”
kann.
@
0
1
sei stetig in den offenen Intervallen (
@
V p
^
!"
V
B
VC
V p
^
VC
V _
!"
V
V _
^
!"
V
VC
VC
VC
!"
V
V \
^
!"
V
Damit ist der Satz vollständig bewiesen.
5
@
¯ ( )) .
5
( )
@ (
Satz: Eine stückweise stetige Funktion
integrierbar.
) = lim
$
r
( )
t
@
( )
@
@
(
@ lim
r
@
bezeichnet, und dies
8
( )
$
ist also überall stetig außer eventuell in endlich vielen Punkten
. Der Wert in diesen Punkten kann, aber muß nicht mit dem
0
linksseitigen oder rechtsseitigen Grenzwert der Funktion übereinstimmen; beispielsweise definiert man Rechteckimpulse gelegentlich auch
durch die Funktion
1 falls 2
1
2 für ein
( )=
.
0 falls
1 falls 2
2 + 1 für ein
u
@
( )
r
wobei ( ¯ ) die Folge der Zwischenwerte zu
zeigt schließlich die Behauptung
B
@ ˜ ( )) ,
1
heißt stückweise stetig, wenn
auf jedem der offenen Interval-
1
B
( )
@
<
(
@
B
¯ ( ) ) = lim
@
8
( )
@
(
u
lim
8
Genauso folgt, daß auch
(2)
6
des Intervalls [ ] gibt, so daß
le (
+1 ) stetig ist.
@
(2)
4
1
0
]
(2) (2)
1 2
=
Definition: Eine Funktion : [
es eine Unterteilung
1
@
=
(2)
3
B
r
(2)
2
(2)
4
@
r
(2)
0
(2)
1
+
(2)
3
]
B
B
u
( )
( )
die Folge der ( ( ) ˜ ), wobei ( ˜ ) irgendeine Folge von Zwischenwerten bezeichnet; wie wir bereits aus dem ersten Schritt wissen, hängt
der Grenzwert nicht davon ab. Also ist
( ) ( )
( ) ˜( )
).
) = lim (
lim (
(2)
2
<
(2)
0
(2)
1
7) Stückweise stetige Funktionen: Gelegentlich möchte man die Bedingung der Stetigkeit wenigstens ein bißchen lockern, um beispielweise
auch einen Rechteckimpuls, der periodisch zwischen 0 und 1 (oder
-1 und 1) wechselt, behandeln zu können. Die Existenz des RIEMANNIntegral wird durch solche kleineren Abweichungen nicht beeinträchtigt:
Kap. 2: Mehrdimensionale Analysis
%
(2)
0
Höhere Mathematik I SS 2007
%
\
V _
^
%
@
v
;
C
9
8
\
(
( )(
1
C
^
)=1
B
@
s C
$
$
s C
^
\ ist
\ h
v
$
$
s C = 0, wie man sich leicht überlegt anhand von Untertei-
x
für die Rechteckfläche auch bei negativer Länge und/oder Breite gelten
soll. Da Integrale nicht nur zur Flächenbestimmung, sondern auch etwa
zur Bestimmung der Ladung in einem Kondensator verwendet werden,
ist dies die Interpretation, die man in der Mathematik in den meisten
lungen, die symmetrisch zur Null liegen. Auch dies läßt sich als Aussage
über Flächeninhalte interpretieren – wenn man davon ausgeht, daß die
Formel
Fläche = Länge Breite
( )
1
auch negative Werte annimmt? Für ( ) =
etwa
= ( ) und der -Achse zwischen den
:
1
Was passiert, wenn
als Fläche zwischen der Kurve
Geraden = und = .
9) Ausblick: Das Lebesgue-Integral: Wir könnten allerdings auch argumentieren, daß es nur“ abzählbar unendlich viele rationale Zahlen,
”
aber überabzählbar viele irrationale zwischen null und eins gibt; da1
her sollten letztere das Geschehen dominieren, und 0 ( )
sollte
verschwinden.
1
) = 0.
0=1
+1
+1
=0
(
g
( )(
=0
( )
)=
)=
+1
eine nichtnegative Funktion, so bezeichnen
Damit kann kein gemeinsamer Grenzwert existieren, und somit ist die
DIRICHLETsche Sprungfunktion nicht RIEMANN-integrierbar – ein sehr
viel überzeugenderes Ergebnis als das aus Abschnitt b3).
=0
C
)=
]
und
\
@
e
(
Definition: Ist : [
wir die Zahl
B
w
1
10) Anwendung auf Flächeninhalte: Nachdem wir nun mit einen exakten Integralbegriff haben, bietet sich an, Flächen über dieses Integral
zu definieren:
<
h
1
Dazu sei eine Unterteilung des Intervalls [0 1]. Unabhängig von der
Wahl dieser Unterteilung können wir stets eine Folge von rationalen
Zwischenwerten finden, aber auch eine Folge von irrationalen. Dann
ist, unabhängig von der Unterteilung ,
0
h
.
( )
1 für
0 für
8
1
( )=
7
9
wir interessieren uns für
8) Noch einmal die Dirichletsche Sprungfunktion: In Abschnitt b3)
waren wir nicht zufrieden mit dem Verhalten des dort heuristisch eingeführten Integrals für die DIRICHLETsche Sprungfunktion; schauen wir,
was das nun eingeführte RIEMANN-Integral daraus macht. Sei also
In der Tat kann man eine Verallgemeinerung des RIEMANN-Integrals
definieren, das LEBESGUE-Integral, das für stückweise stetige Funktionen mit dem RIEMANN-Integral übereinstimmt und für die DIRICHLETsche Sprungfunktion den Wert Null liefert. Dazu geht man nach dem
französischen Mathematiker HENRI LÉON LEBESGUE (1875-1941) bei
den Unter- und Obersummen nicht wie bei RIEMANN von endlich vielen
Rechtecken aus, sondern von abzählbar unendlich vielen. (Wie man dies
im einzelnen macht, braucht uns hier nicht zu interessieren; wir werden
uns im folgenden stets auf das RIEMANN-Integral beschränken.) Dieses
LEBESGUE-Integral existiert fast immer: Man kann zwar die Existenz
von Funktionen, für die es nicht existiert, beweisen,explizite Beispiele
solcher Funktionen sind aber nicht bekannt.
Nun gibt es aber in jeder Unterteilung nur endlich viele Intervalle, die
ein enthalten, und auch die Sprunghöhen sind begrenzt; gehen also
alle Intervallängen gegen Null, so geht auch wie im Beweis des Satzes
die Differenz zwischen RIEMANNschen Ober- und Untersummen gegen
Null.
Kap. 2: Mehrdimensionale Analysis
%
Höhere Mathematik I SS 2007
v
h
%
w
e G
m
h
G
g
w
g
e
B
( )
.
g
@
C
JzJKJK JKJKJ
h
m
C
JzJKJKJKJKJ
g
C
w
g
e
e
h
h
$
g
C
w
h
g v
C
)
\ \ {
m
m
\ ^
g
w
e
,
e
y
h
g
m
g
m
G
w
w
e
$
e G
h
G
.
g
JzJKJzJKJKJ
h
m
G
w
JzJKJzJKJKJ
m
g
e G
w
e
( )
e G
( )
( )
m
d.h.
w
( )
( )
( )
G
( )
G
( )
G
G
und erhalten
,
Insbesondere können wir dies auch anwenden auf die Ungleichungskette
( )
h
wie behauptet.
w
( )
ist. Da sich eine solche Kleinergleichbeziehung auch auf Grenzwerte
überträgt, ist daher
(
y
C
)
{
(
Beweis: Wir betrachten eine Unterteilung des Intervalls [ ] und
eine dazu kompatible Sequenz von Zwischenwerten; (
) sei die
zugehörige RIEMANN-Summe für und (
) die für . Da für jedes nach Voraussetzung ( )
( ) ist, folgt unmittelbar aus der
Definition der RIEMANN-Summen, daß
C
h
1) Monotonieregel: Eine der einfachsten, aber trotzdem oft nützlichen
Regeln für den Umgang mit Integralen übersetzt Größerbeziehungen
zwischen Integranden in Größenbeziehungen zwischen Integralen:
e
e G
\
y
In diesem Abschnitt sollen die ersten (und einfachsten) solchen Regeln zusammengestellt werden; danach erweitern wir zunächst unser
Instrumentarium, um dann damit auch kompliziertere und interessantere Regeln zu beweisen.
w
w
\ Das RIEMANN-Integral stellt die heuristischen Überlegungen vom Beginn dieses Paragraphen insofern auf eine exaktere mathematische
Grundlage, als wir nun einen Integralbegriff haben, der auch bei extrem
ungewöhnlichen Funktionen wie der DIRICHLETschen Sprungfunktion
keine unerwarteten Ergebnisse liefert. Was allerdings den Ausgangspunkt betrifft, die Umkehrung der Differentiation, wissen wir über das
neue Integral noch gar nichts, und auch sonst kennen wir noch nicht
viele Regeln über den Umgang damit und insbesondere auch über seine
Berechnung ohne die umständlichen und sehr langsam konvergierenden
RIEMANN-Summen.
h
g
( )
( )
^
d) Erste Integrationsregeln
y
Insbesondere ist
( )
e
C
= 0.
@
w
y
( )
@
Insbesondere ist dann natürlich
G
.
B
@
( )
h
=
8
B
def
B
h
( )
y
Im Sinne dieser negativen Längen und Breiten ist es auch sinnvoll,
zu definieren durch
Integrale für
m
arbeiten.
und seien stückweise stetige Funktionen auf dem Inter], und für alle
[ ] sei ( )
( ). Dann ist auch
( )
Satz:
vall [
Kap. 2: Mehrdimensionale Analysis
%
Fällen vorzieht; für die klassische Fläche im Sinne des Tapezierens muß
man mit
Höhere Mathematik I SS 2007
h
m
g
JKJzJKJKJKJ
h
JKJzJKJKJKJ
g
g
$
%
y
@
}
+
1
( )
.
w
w
w
e
h
e
h
e
| h
}
y
}
g
g
|
y
|
g
C
\
.
sei stück], so daß
B
@
@
w
e
w
m
~ e
]
.
gibt es ein
C
g
@
h
~ e
h
e
h
B
$
~
[
]
Mit anderen Worten: Der Mittelwert“ der Funktion im Intervall [ ]
”
existiert nicht nur, sondern wird auch an (mindestens) einer Stelle im
Intervall angenommen.
( )
( )=
1
Korollar: Für eine stetige Funktion : [
mit
C
m
<
1
w
g
g
h
v
g
@
B
y
B
@
l
m
y
c
B
8
@
w
y
m
y
y
w
e
w
( ) ( )
( )
l
und damit nach der Monotonieregel
c
( )
.
Zum Beweis des Satzes betrachten wir das Minimum und das Maximum
von auf [ ]. Da nirgends negativ wird, gilt dann auch für
jedes
[ ]
( )
( ) ( )
( )
3) Der Mittelwertsatz der Integralrechnung: Der Mittelwertsatz der
Differentialrechnung ist der wohl wichtigste Satz aus der Analysis I.
Mit dieser überragenden Bedeutung kann der Mittelwertsatz der Integralrechnung nicht konkurrieren; trotzdem ist auch er eine sehr nützliche Aussage, die insbesondere auch die zu Beginn dieses Paragraphen postulierte Interpretation von Integralen als Mittelwerten für das
RIEMANN-Integral auf eine solide Grundlage stellt.
y
@
beliebigen Folge sich verfeinernder Unterteilungen von [ ] berechnet werden; insbesondere können also Unterteilungen gewählt werden,
die den Zwischenpunkt enthalten, und dafür folgt die Behauptung
unmittelbar.
1
h
kann als Grenzwert von RIEMANN-Summen zu einer
g
B
( )
Beweis:
y
.
( )
e
@
+
w
y
1
( )
h

B
=
C
g
@
( )
e
y
Die Funktion sollte man sich dabei als eine Gewichtsfunktion“ vor”
stellen, die die verschiedenen -Werte verschieden stark gewichtet. Am
anschaulichsten ist der Spezialfall
1, der deshalb noch einmal getrennt angegeben sei:
<
]
w
8
und eine stückweise stetige Funktion : [
( )
h
B
Satz: Für
ist
y
= ( )
C
( ) ( )
[
@
Für die Zusammensetzung von Integrationsintervallen gilt erwartungsgemäß
@
8
Beweis: Wie beim letzten Satz: Für jede RIEMANN-Summe zu einer festen Unterteilung und jede damit kompatible Zwischenwertsequenz
gilt die zur Behauptung des Satzes analoge Gleichung, und damit gilt
im Limes auch der Satz selbst.
B
B
( )
@
=
<
]
B
Satz: : [ ]
sei eine stetige Funktion; : [
weise stetig und nirgends negativ. Dann gibt es ein
1
( )
und zwei
<
( )+
]
B
:[
<
Satz: Für zwei stückweise stetige Funktionen
reelle Zahlen
ist
Im Hinblick auf spätere Anwendungen sei der Satz zunächst etwas
allgemeiner formuliert, als wir ihn im Augenblick bentigen; an der
Schwierigkeit des Beweises ändert diese Verallgemeinerung nichts.
Kap. 2: Mehrdimensionale Analysis
2) Linearität und Zusammensetzung: Genauso einfach ist die Linearitätsregel:
Höhere Mathematik I SS 2007
%
h
e
y
l
h
h
e
y
g
m
g
m
c
g
%
Es gibt daher eine reelle Zahl
daß
c
w

w
e
l
h
e
h
y
g

y
g

C
C
B
8
@

y
@
$
;
7
e
$
g
$
g
h
e
h
$
$
C
C

G
G
$
C
g
g

.
g

g
eine weitere Funktion mit Ableitung , so hat die Differenz von
und
die Ableitung Null. Nun erinnern wir uns an die Analysis I:
Wenn die Ableitung einer Funktion ( ) verschwindet, muß die Funktion konstant sein. In der Tat: Gäbe es im Definitionsbereich von zwei
Werte 1 = 2 mit ( 1 ) = ( 2 ), so gäbe es nach dem Mittelwertsatz
der Differentialrechnung ein
( 1 2 ), so daß
( 2)
( 1)
= ( )
Ist
Geht nun gegen Null, so muß die zwischen und + liegende Zahl
gegen gehen; wegen der Stetigkeit von ist also ( ) = ( )

.
<
B
@

8
C
$
w

$
e
wäre. Hier steht links eine von Null verschiedene Zahl, rechts aber Null,
ein Widerspruch.
1
2
C
C
.
*
Nach dem Mittelwertsatz der Integralrechnung aus dem vorigen Abschnitt gibt es in jedem der beiden Fälle ein zwischen und + , so
daß das Integral gleich
( ) ist, d.h.
( + )
( )
= ( ).
C

( )
( )

( )=
g

sei

+
( )
]
$
( )=
*
C
Hauptsatz der Differential- und Integralrechung: : [
eine stetige Funktion und
( + )
=
+

Eine Motivation zur Einführung eines Integrals war die Suche nach einer
Umkehroperation zur Differentiation: Genau wie die Differentiation aus
einem zeitabhängigen Weg eine Geschwindigkeit macht, wollten wir
ausgehend von einer zeitabhängigen Geschwindigkeit den Weg zurückbekommen. Der Hauptsatz der Differential- und Integralrechnung sagt
uns nun endlich, daß wir dieses Ziel erreicht haben:
g
ist entsprechend
( )
;
e) Der Hauptsatz der Differential- und Integralrechnung
g
(s. Abschnitt b)); für negatives
( )
nicht in der Form ( ) darstellbar.
e

*fe
1

( )
h $
1
y
*
h
0
B
( )
g
( )=

+
( + )
g
( + )
!
g
1
).
*e
1
=
2
(
1

ist

( ) = lim

1
=
2
für positives
0
ist
g
h
1

g
1
( 1)
Beweis: Die Ableitung von
$
ist

*
e
0
0
@

nur eine stückweise stetige
g
B
h
Man beachte, daß es hier nicht genügt, daß
Funktion ist: Für
0 für
( )=
1 für
g
Damit ist der Satz bewiesen, und das Korollar ist natürlich einfach der
Spezialfall
1, für den das Integral über gleich
ist.
ist, und da stetig ist, gibt es nach dem Zwischenwertsatz mindestens
ein
[ ], für das ( ) = ist.
( ) = ( ) für alle

Ist umgekehrt
eine differenzierbare Funktion, deren Ableitung auf
dem offenen Intervall ( ) mit übereinstimmt, so gibt es eine reelle
Zahl derart, daß ( ) = ( ) + ist.
Dann ist
8
@
( )
, den Mittelwert, so
B
( ) ( )
und
Kap. 2: Mehrdimensionale Analysis
=
zwischen
Höhere Mathematik I SS 2007
%
1
h
g
g
%
oder

g
B
@
w
e
@
h
)
h
B
h
@
$
g

h
$

e
B g
B g
B
@
$

e
C
C
h

h
.
)
ist eine Stammfunktion von

Beweis: Klar, denn
-
= ( )+
g*
cos
=
=
sin
= 0,
1
+
Unter den trigonometrischen Funktionen sind zumindest der Sinus und
der Cosinus aus der Analysis I bekannt; die meisten kennen wohl auch
Die Arkusfunktionen sind die Umkehrungen der trigonometrischen
Funktionen: Letztere ordnen einem Winkel eine reelle Zahl zu; die Umkehrfunktionen liefern also als Ergebnis einen Winkel oder auch Bogen,
auf lateinisch arcus genannt.
Die Ableitung einer rationalen Funktion ist wieder eine rationale Funktion; für Stammfunktionen gilt allerdings nicht dergleichen, denn wie
wir gerade gesehen haben, ist schon die Stammfunktion von 1 nicht
mehr rational, sondern der natürliche Logarithmen. Wie wir bald sehen
werden, reichen (im Reellen) auch Logarithmen noch nicht aus, um alle
rationalen Funktionen integrieren zu können; wir brauchen zusätzlich
noch die sogenannten Arkus- und Areafunktionen.
f) Trigonometrische Funktionen, Hyperbelfunktionen und ihre Umkehrfunktionen
sind nun problemlos. Für weitere Stammfunktionen müssen wir allerdings zunächst noch einige Funktionen kennenlernen.

( )
)
Korollar:
h
g*
Diese Nichteindeutigkeit sorgt auch dafür, daß zwar nach obigem Hauptsatz die Differentiation die Integration rückgängig macht, die Integration
umgekehrt aber die Differentiation nur bis auf auf eine Konstante:
e
die Nichteindeutigkeit der Stamm-
e

wobei die Integrationskonstante
funktion ausdrückt.
@
,
-
h
h
+
h
@
( )
)

( )=
falls
falls

heißt Stammfunktion
g*
und
+1
Definition: Eine differenzierbare Funktion
von , wenn ( ) = ( ) ist; wir schreiben
=
+1

Für einfache“ Integranden ist dies im allgemeinen die beste Möglichkeit
”
zur Berechnung eines Integrals; die Funktionen haben daher einen
Namen verdient:
=
+
e
g*
und auch Formeln wie
cos
sin
=
h
.
Beweis: Mit obigen Bezeichnungen ist das Integral gleich ( ). Zur
Funktion gibt es nach dem Hauptsatz eine Konstante , so daß ( ) =
( ) + ist. Damit ist ( )
( ) = ( ), wie gewünscht.
$
=
1
=
( ).
g
( )
also ganz einfach. Eine erste Auswahl von Stammfunktionen erhalten
wir durch Rückwärtslesen von Differentiationsregeln, zum Beispiel
=
h
$
.
( )
irgendeine differenzierbare Funktion mit der EigenKorollar: Ist
schaft, daß ( ) = ( ) ist im Intervall [ ], so gilt
e
( )
( )
kennen, ist die Berechnung des
B
( )
=
Falls wir eine Stammfunktion von
Integrals
@
Als Anwendung für die Berechnung bestimmter Integrale ergibt sich
das folgende
( )+
$
w
ist, wie behauptet.

( )=
g
( )=

( )
, so daß
Also gibt es eine Konstante
Kap. 2: Mehrdimensionale Analysis
%
Höhere Mathematik I SS 2007
%
%
u
8
k
k
k
4
=

2
2
Da alle trigonometrischen Funktionen periodisch sind, können sie keine
global definierten Umkehrfunktionen haben; wir müssen sie also jeweils
3
3
=
3
3
?
1
=
6
=
0
$
0
$
tan
-1.5
-1
-0.5
00
Abb. 56: Der Arkussinus
$
0.5
x
1
]
1
]
[ 1 1] .
[0
$
cos: [0
ist die Umkehrfunktion von
arccos: [ 1 1]
Der Cosinus fällt von seinem Maximalwert 1 an der Stelle Null monoton
ab, bis er bei den Wert 1 erreicht hat. Wir definieren den Hauptwert
der Umkehrfunktion Arkuscosinus oder kurz den Arkuscosinus daher
für dieses Intervall:
-0.5
1$
Abb. 55: Der Tangens
$
-4
-1
0.5

-2
6
x4
1
Aus den speziellen Werten von Sinus und Cosinus berechnet man leicht
die entsprechenden Werte für Tangens:
2
1.5
1$
00
$

[ 1 1] .
-2

2 2
-4
$
sin:

-6
2
4
Im Fall des Sinus bietet sich das Intervall von
2 bis 2 an, in dem
er monoton von 1 auf 1 ansteigt; wir definieren daher den Arkussinus
oder – genauer ausgedrückt – den Hauptwert des Arkussinus für dieses
Intervall:
arcsin: [ 1 1]
2 2
ist die Umkehrfunktion von
mit
verschwindet, ist tan an diesen
Da cos für = 2 +
Stellen nicht definiert; in ihrer Umgebung wird er links, wo Sinus und
Cosinus dasselbe Vorzeichen haben (+ für gerades , für ungerades)
beliebig groß, rechts beliebig negativ; siehe dazu auch Abbildung 55.
auf ein Intervall einschränken, auf dem sie injektiv oder – besser noch –
monoton sind.
sin
,
tan =
cos
den Tangens. Im rechtwinkligen Dreieck gibt er das Verhältnis zwischen
Gegenkathete und Ankathete eines Winkels an und damit das, was man
üblicherweise als Steigung bezeichnet: das Verhältnis der Höhendifferenz zur horizontalen Entfernung.
Kap. 2: Mehrdimensionale Analysis
%
bereits deren Quotienten
Höhere Mathematik I SS 2007
1$
%
Abb. 57: Der Arkuscosinus
00
0.5
1
1.5
0.5
x
1
$
<
1$
'
2
4
x
6
8
:

)
$

.
q
:
1
(
=
= arccos
:
= arctan
= arcsin
= 4 arctan(1) .
= 0 auch so etwas wie
gelten. Dies im Prinzip auch richtig, allerdings nicht immer für den
Hauptwert: Da alle drei Umkehrfunktionen nur Werte in einem Intervall der Länge annehmen, während das Argument (genauer: der

Falls man in einem Programm den Wert benötigt und ihn über diese
Formel als Programmkonstante definiert, kann man – eine saubere Implementierung der Arkusfunktionen vorausgesetzt – sicher sein, daß
2
2
:
für
=
+
Mit Hilfe der Arkusfunktionen lassen sich die Polarkoordinatendarstellung und die kartesische Darstellung der komplexen Zahlen ineinanRealteil
= cos und Imaginärteil
der umrechnen: Da =
= sin hat, sollte außer der bereits bekannten Formel
Abgesehen vom gerade definierten Hauptwert lassen sich natürlich noch
in offensichtlicher Weise weitere Zweige definieren; wir wollen hier auf
Einzelheiten verzichten. Der Leser sollte sich allerdings klarmachen,
daß es beispielsweise für den Arkussinus sowohl monoton wachsende
als auch monoton fallende Zweige gibt.

Gelegentlich ganz nützlich ist der Wert an der Stelle 1: Da nach obiger
Tabelle tan 4 den Wert 1 hat, ist arctan(1) = 4 oder
.
<
2 2
(
tan:
2 2
-1.5
-1
-0.5
00
Abb. 58: Der Arkustangens
-2

ist die Umkehrfunktion von
'
arctan:
-4
mit der maximal möglichen Stellenzahl der jeweiligen Gleitkommaarithmetik dargestellt wird – ohne daß man diese Stellenzahl oder gar
mit der entsprechenden Genauigkeit zu kennen braucht.
-6
Der Tangens schließlich ist monoton ansteigend im offenen Intervall
2
2) und nimmt dort jeden reellen Wert an; wir definieren den
(
Hauptwert der Umkehrfunktion Arkustangens oder kurz den Arkustangens daher für dieses Intervall:
-0.5
$
2
-8
0.5
1
1.5
-1

2.5
=
$
3

arcsin .
und der Wahl der Werte-
2
Kap. 2: Mehrdimensionale Analysis
%
Aufgrund der Beziehung cos = sin
bereiche ist
arccos =
2
Höhere Mathematik I SS 2007

=
%
q
$
*
arg =
;

q
r
q
*
7
$
r
y
y
y
:
:
$
$
=
+
2
und
sin
=
*
*
)
)
)
*
$
= arcsin +
2
+
und sinh =
2
2
zu definieren, den Cosinus hyperbolicus und den Sinus hyperbolicus.
cosh
neue Funktionen
=
*
cos
)$

$
)
.
? $
$
? $
$
2
cosh
sinh
2

$
2
+
2
)
2
2+
4
)
)
)

+2+
4
2

2
+
2

=
=
2
2
Der Zusatz hyperbolicus läßt sich leicht verstehen: Genau wie der
gewöhnliche Sinus und Cosinus als Kreisfunktionen bezeichnet werden, weil die Punkte (sin cos ) auf dem Kreis 2 + 2 = 1 liegen,
haben die Hyperbelfunktionen ihren Namen daher, daß
2
*

= 1 + tan
und
)$

cos2 + sin2
cos2
2
:
=1

=
$
)
)
sin
cos
2
1+ 2
mit dem jeweils anderen Vorzeichen bekommen können. Eine offensichtliche Lösung besteht darin, einfach durch zu ersetzen, und das
legt es nahe, in Analogie zu den EULERschen Formeln
1
e
*
tan ( ) =
e
*
Für den Arkustangens schließlich müssen wir zunächst Tangens selbst
ableiten; nach der Quotientenregel ist
h
*
2
2], in dem der Arkussinus seine
da der Cosinus im Intervall [
Werte annimmt, größer oder gleich Null ist, folgt
1
2 und
.
arcsin ( ) =
cos(arcsin ) = 1
2
1
Genauso ist
1
1
arccos ( ) =
=
,
2
sin(arccos )
1
da der Sinus zwischen 0 und keine negativen Werte annimmt.
h
h
;
h
e
sin (arcsin ) = 1
?
cos (arcsin ) = 1

2
e
h
2
? $
h
2
1
Als nächstes wollen wir uns überlegen, wie wir die Integrale
und
= 1 ist
= arctan +
2
h
1+
h
Wegen sin2 + cos2
.
für die Umkehrfunktion einer Funktion . Da die Ableitung des Sinus
der Cosinus ist, erhalten wir also
1
arcsin ( ) =
.
cos(arcsin )
2
Da sich die Ableitungen von Arkussinus und Arkuscosinus nur im Vorzeichen unterscheiden (was natürlich von vornherein klar war, da sich
die Werte der beiden Funktionen stets zu 2 ergänzen) sind als Stammfunktionen vor allem der Arkussinus und der Arkustangens interessant;
wir haben die beiden neuen Formeln
1
1
=
1 + tan2 (arctan ) 1 +

Wie in der Analysis I bei der Ableitung des Logarithmus gehen wir aus
von der Formel
1
( )=
( )
Der für uns interessanteste Aspekt der Arkusfunktionen sind ihre Ableitungen, die uns neue, bislang unbekannte Stammfunktionen liefern
sollen.
0
.
0
arctan ( ) =
falls
falls
und dementsprechend
Kap. 2: Mehrdimensionale Analysis
arccos
arccos
Hauptwert des Arguments) einer komplexen Zahl im doppelt so langen
] liegt, kann obige Gleichung bei keiner der drei FunkIntervall (
tionen für alle gelten. Eine korrekte Formel mit dem Hauptwert des
Arkuscosinus ist beispielsweise
Höhere Mathematik I SS 2007
%
)
)$

)
$
)
$
h
h
%
ist, so daß die Punkte (cosh sinh ) auf der Hyperbel
d.h
2
2
cosh
sinh = 1 für alle
Höhere Mathematik I SS 2007
$
<
8
$
;
= 1 liegen,
8
;
.
sinh
= cosh ;
auf Grund obiger Ungleichung ist daher der Sinus hyperbolicus monoton
steigend auf ganz . Man sieht leicht, daß sein Vorzeichen jeweils das
von ist (Insbesondere ist also auch sinh 0 = 0.), d.h. der Cosinus
hyperbolicus ist monoton fallend für negative und monoton steigend für
positive .
cosh ( ) = sinh
und
Sofort aus der Definition folgen die Ableitungsregeln
1 für alle
<
cosh
Damit ist insbesondere cosh stets 1; da der Cosinus hyperbolicus
genau wie die beiden Exponentialfunktionen, aus denen er zusammengesetz ist, keine negativen Werte annehmen kann, folgt also
.
2
:
2
2
<
*
1
*
)
L
Für große Werte von wird
beliebig klein, sowohl sinh als
auch cosh unterscheiden sich für solche Werte also beliebig wenig
von 21 und gehen insbesondere gegen unendlich. Für stark negative
Werte wird beliebig klein und das Verhalten beider Funktionen wird
dominiert durch den Term
. Daher geht sinh für
gegen
und cosh gegen + . Offensichtlich ist sinh eine ungerade,
cosh aber eine gerade Funktion. In Abbildung 59 sind gestrichelt auch
noch die Funktionen 12 im positiven und 12
im negativen Bereich
eingezeichnet; wie man sieht, ist die Übereinstimmung mit sinh bzw.
cosh schon ab etwa
2 recht gut.
*
)
)
*
!"
*
*
)
!"
*
)
L
*
)
!"
*
2
$
!"
$
*
*
)
2
)
)
*
3
2
)
)
2
+1
= 1.
1
Die Ableitung des Tangens hyperbolicus ist nach der Quotientenregel
*
= lim
* $
)
+
=1
(1 +
(1
*
*
)
*
2
"
!
*
)
)$
"
!
*
"
!
*
2
$
*
G ;
G
)
*
7
$
$
Aus beiden Ausdrücken sieht man sofort, daß die Ableitung stets positiv
ist, der Tangens hyperbolicus steigt also monoton von 1 nach +1,
wobei beide Werte nur asymptotisch angenommen werden.
tanh
=
1
cosh2
sinh2
nach obiger Formel
cosh2
=
,
2
2
cosh
1 tanh
durch Ausdividieren
wobei wie beim Tangens je nach Anwendung mal die eine, mal die
andere Form des Ergebnisses nützlicher ist.
)$
*
;
)$
$
*
=
*
*
= lim
)
2
= lim
*
lim tanh
)
1+
1
)
= lim
+
*
)
und entsprechend
= lim
*
)
tanh
lim tanh
*
*
+
2
)
sinh
=
def cosh
1
*
In völliger Analogie zum Tangens definieren wir auch noch einen Tangens hyperbolicus durch die Vorschrift
-10
-5
0
<
Der Graph des Cosinus hyperbolicus erinnert an eine durchhängende
Kette, und tatsächlich kann die Variationsrechnung zeigen, daß eine
Kette mit reibungsfrei gegeneinander beweglichen Gliedern genau diese
Form hat.
-1
Abb. 59: Sinus hyperbolicus und Cosinus hyperbolicus
-2
da der Cosinus hyperbolicus stets größer oder gleich eins ist, kann der
Nenner nie Null werden, so daß die Funktion auf ganz definiert ist.
Dabei ist
-3
5
10
Kap. 2: Mehrdimensionale Analysis
%
$
)
*
)
)
*
)$
-1
-0.5
00
1
x
Abb. 60: Der Tangens hyperbolicus
-1
2
3
1
<
<
artanh: ( 1 1)
definiert ist und der Areatangens hyperbolicus
<
<
1
$
<
1
0
<
1
2
und
5
x
4
x
6
8
Abb. 61: Der Areasinus hyperbolicus
-3
-2
-1
00
1
2
arsinh ( ) =
1
=
sinh(arcosh )
arcosh ( ) =
1
=
cosh(arsinh )
1
1
2
1
1+
2
Abb. 62: Der Areacosinus hyperbolicus
-5
Rechnung zeigt, daß
0
0.5
1
1.5
2
2.5
3
-10
?
Auch diese Funktionen sind wieder vor allem wegen ihrer Ableitungen interessant; eine weitgehend zum Fall der Arkusfunktionen analoge
Da Sinus hyperbolicus und Cosinus hyperbolicus asymptotisch wie eine
Exponentialfunktion ansteigend, steigen Areasinus hyperbolicus und
Areacosinus hyperbolicus wie Logarithmen, also sehr langsam.
als die Umkehrfunktion des positiven Zweigs.
arcosh:
nur auf dem offenen Einheitsintervall. Der Cosinus hyperbolicus hat
keine eindeutig bestimmte Umkehrfunktion, da er für positive und für
negative Argumente jeweils denselben Wert annimmt. Wir definieren
den Areacosinus hyperbolicus
auf ganz
arsinh:
Aus obiger Diskussion folgt, daß der Areasinus hyperbolicus
Die Umkehrfunktionen der Hyperbelfunktionen werden als Areafunktionen bezeichnet und heißen Areasinus hyperbolicus, Areacosinus hyperbolicus und Areatangens hyperbolicus.
-2
0.5
3
Kap. 2: Mehrdimensionale Analysis
10
10
%
-3
%
1
Höhere Mathematik I SS 2007
%
? $
%
-0.8
-0.6
$
h
h
$
?

? $
e
h
e
e
$
h
)
y
v
$
$
und
*
h
2
=
e
=
2
)$
*
2
=(
2
$
*
h

G G
e
h
e

G G $
$
wobei diese Formel noch den Vorteil eines größeren Definitionsbereichs
hat.
)$
*
2
*
=(
1)
+
1
.
2 + 2)
auf eine Stammfunktion. Genauso lassen sich rekursiv auch die Integrale
berechnen:
)
1
e
e
,
h
h
+
*
*
=
)$
+ ln 1 +
2
*
+
*
ln 1
*
)
ist, können wir dieses Integral auch ausrechnen als
*
1
1+

$
+
)
+
1
=
1
e
=
y
)
1
2
Mit den wenigen Funktionen, die wir bislang kennen, lassen sich nur
wenige interessante Beispiele konstruieren; die volle Kraft dieser Regel werden wir erst später kennenlernen, wenn wir unser Repertoire
betrachtet: Da
an Funktionen erweitert haben. Hier sei nur
die Exponentialfunktion ihre eigene Ableitung und Stammfunktion ist,
empfiehlt sie sich für die Rolle der Funktion , während ( ) = mit
( ) = 1 auf Vereinfachungen auf der rechten Seite hoffen läßt. In der
Tat führt partielle Integration mit
y
*
=
( ) ( )
2
( ) ( ),
führt – die Regel der partiellen Integration. Sie ist dann nützlich, wenn
sich der Integrand als Produkt schreiben läßt, wobei einer der Faktoren
eine bekannte Stammfunktion hat; gelegentlich ist dann das Produkt
( ) ( ) leichter integrierbar als ( ) ( ).

1
1
e
Die letztere wird allerdings nicht unbedingt gebraucht, denn da
y
.
= artanh( ) +
y
2
h
v
1
y
h
und
y
= ( ) ( )
$
= arcosh( ) +
( ) ( )
( ) ( )
y
1
was integriert auf
( ) ( )=
$
2
Für die Zwecke der Integralrechnung schreiben wir sie besser als
e
= arsinh( ) +
h
h
2
h
*
1+
h
y
Dies führt also auf die neuen Stammfunktionen
.
2
y
y
1
1
=
tanh2 (artanh ) 1
1
artanh ( ) =
h
Abb. 63: Der Areatangens hyperbolicus
0.8
-2
0.4 x 0.6
y
-1
0.2
00
-0.2
( ) ( )+ ( ) ( ).
( ) ( ) =
y
-0.4
1
Eine wichtige Regel der Differentialrechnung ist die Produktregel
g) Partielle Integration
Kap. 2: Mehrdimensionale Analysis
%
ist. Für den Areatangens hyperbolicus schließlich ist
2
Höhere Mathematik I SS 2007

)
*
)
h
)
e
*
)$
h
)
)
)
%
( )
y
h
y
y
h
y
y
h
y
y
e

h
y
y
G
G
y
h
y
e
y
ln(1 +
1
2
ln(1 +
1+
@
@
y
y
y
y
$
@
h
B
e
y

e
+ )
@
2
2
2
)+
.
+
)+
( )= ( )
+ )
+
( ) = ( ).
@
$
@

G
G
h
$
e
h
=
mit
cos(
+ )
mit
sin(
+ )
eine Funktion, die genau wie der Tangens selbst an den Nullstellen der
Cosinusfunktion nicht definiert ist.
(
(
Somit ist beispielsweise
=
+ )
=
@
,
B
ln cos( ) +
1
2
=
e
tan
=
(
h
ist, oder besser
B
+ )
(
mit ( ) = cos . Nach der gerade bewiesenen Regel ist daher
B
=
B
tan
( )
( )
sin
=
cos
Als erste Anwendung betrachten wir
arctan
=
$
.
arctan
=
= ln ( ) +
+
$
( )
( )
2) Substitutionen mit linearen Funktionen: Eine der elementarsten
Anwendungen der Substitutionsregel, auf die man üblicherweise auch
ohne diese Regel kommt, ist die Substitution mit linearen Funktionen
( )=
+ ; hier besagt die Substitutionsregel, daß
ist.
1 arctan
e

zur Integrationsregel
2
( )= ( )
ln 1 +
e
mit
( ) +
e
h
=
Damit können wir dann beispielsweise den Arkustangens integrieren:
Partielle Integration zeigt, daß
1
2
JzJKJ
h
( )
=
JzJKJ

( )
h
2

1+
führt
,

1) Der Spezialfall logarithmischer Ableitungen: Für ( ) = 1
die Substitutionsregel
Diese Regel dürfte wohl meist der erfolgversprechendste Versuch zum
Auffinden einer Stammfunktion sein – vor allem, wenn man sie von
rechts nach links liest, um für eine bekannte Funktion die unbekannte
Stammfunktion
zu berechnen. Als Substitution wählt man hier
eine geeignete“ bijektive Funktion, die zu einer Vereinfachung auf der
”
linken Seite führt.
2
lassen sich nach dieser Regel ausrechnen: Da die Ableitung des Nenners
2 ist, folgt
1+
e
ist.

,
eine Stammfunktion von
( ) +
Auch Integrale wie
h
wobei
e
=
da der Cosinus hyperbolicus nur positive Werte annimmt.
( )
h
= ln cosh( ) +
( )
e
= ln cosh( ) +
G
tanh
G
( )

( ) =

läßt sich umschreiben zu einer Integrationsregel, der Substitutionsregel
Auch die Kettenregel
Beim Tangens hyperbolicus gibt es keine Probleme mit dem Vorzeichen;
hier ist ganz entsprechend
Kap. 2: Mehrdimensionale Analysis
%
h) Substitutionsregel
Höhere Mathematik I SS 2007

%
2
6
2
*
e
h
e
2
*
@
g
e
h
2
@
h
$
@
$

@
B
e
@
@
+
@
B
h
@
:
@
h
e
@
(
'
:
h
e
:
@
B
@
h
&
h

6
6

@
0 ,
h
@

(
'
6

6
h
h $
'
(
w
g*
h
e
+
sinh2 cosh
o

B $

=
2
cosh
,
Leider kennen wir das rechtsstehende Integral noch nicht; angesichts
der großen Ähnlichkeiten zwischen trigonometrischen Funktionen und
w
o
B
@
0.
da cosh nur positive Werte annimmt.
1
falls
=
h

(
+
.
'
2
o
=0
2
h

g*
artanh
@
+
h
o
falls
e
+
2
+
@
2
+
2
?
1+
h
2
e
$
=
$
e
2

0
falls
? $
+
+ arcsin ) +
+
2
e
2
1
arctan
= 21 (
1
Aus ähnliche Weise läßt sich auch die Stammfunktion von 1 + 2
bestimmen: Hier bietet sich die Substitution
= sinh an und wir
erhalten
2
sin2 (arcsin ) =
2

1
h
falls
das Ergebnis
1
.
erhalten wir schließlich nach der
+
nur nichtnegative
?
und je nach Vorzeichen von kann dies entweder über eine der obigen
Formeln oder (für = 0) elementar ausgerechnet werden. Insgesamt
4 2)
erhalten wir mit = 2 4 (und damit =

artanh
2
$
=0
0
falls
falls
und
,

1
$ @
+
cos(arcsin ) =
$
1

1
h
Mit der Rücksubstitution = arcsin
kurzen Nebenrechnung
=
@
arctan

1
+
2
sin2 cos
= 21 (sin cos + ) +
h
2
$
1
2
cos
=
B
+
2
B
ist dann
B
2
B
4
v
Dieses Integral kennen wir von Aufgabe 1b) des dritten Übungsblatts:
e
2
$
h

=
und
+
h
=
e
2
$
, da Cosinus zwischen
$
Mit
$
.

1
=
4

=
+
=
2
e
und dies ist cos2
Werte annimmt.
2
=
1
+
=1
2
Betrachten wir als einfachstes Beispiel die Stammfunktion von 1
selbst. Mit der Substitution = sin mit 2
2 erhalten wir
(durch Rückwärtslesen der Substitutionsregel)
h
+ =
2
m
+
sinh
=
2
2
cosh
? $
2
= 1 und
2
2
+ cos
m
Da der Fall = 0 uninteressant ist (bzw. eine unbedingt notwendige
Übungsaufgabe für alle, die nicht sofort einsehen warum), schließen wir
dies aus und schreiben
:
'
+
@
+
(
+
2
?
bieten sich Substitutionen mit trigonometrischen Funktionen und Hyper2
belfunktionen an bei Integralen, in denen Ausdrücke der Form 1
und ähnliche vorkommen.
sin
und sogar ganz allgemein
@
artanh
.
1
+
=
arctan
$
2
=
3) Substitutionen mit trigonometrischen und Hyperbelfunktionen:
Wegen der Beziehungen
L
2
g
+1
'
Entsprechend berechnet man auch
=
(
2

+
1
Kap. 2: Mehrdimensionale Analysis
%
oder
Höhere Mathematik I SS 2007
%
o
&

w
g*

%
%
h
h
e
e
?

?
h

e
$
h
=
m
m
=
$

e
$
h
h
e
$
$

e
e
e $
h
$
$

zu
( )
=
=
(
( )
)
,
;
)
3

$
h
e
$
h
g*
h
3

=
@
=
=
oder
wobei man letztere Beziehung auch aus
=
Im allgemeinen schreibt man eine Substitution wie die obige kurz in der
Form
=
,
3
h

.
y
g*
+
3
2
( )

h
1
3
e
h
= arcsin +
1
@
3
@
= arcsin + cos(arcsin ) +
3
h
3
3
3
1
1+
h
=
y
3
h
Damit ist
h
.
)
( )=
3
( )
3
insbesondere wird das Integral also bei rationalem auf ein Integral
einer rationalen Funktion zurückgeführt, und dieses kann nach dem
im nächsten Abschnitt skizzierten Verfahren der Partialbruchzerlegung
berechnet werden.
wird wegen
e
y

= + cos +
? $
g*
e
)
sin )
3
(1

h
g*
h
=
v
)
sin
cos
cos
? $

1
g*
=
$
3
sin )2
cos
sin2
1
1+
g
( ) : Bei solchen Integralen führt oft die
4) Integrale der Form
oder, anders ausgedrückt, = ( ) = 1 ln zu
Substitution =
einer Vereinfachung. Die Substitutionsregel
=
3
(1
1
?
y
Hier hilft nun ein Trick weiter: Erweitern wir den Bruch unter der
Quadratwurzel mit 1 sin , so wird das Integral zu
h
e
.
=
? $
h
1 sin
cos
1 + sin
1
1+
$
Da es in diesem Abschnitt um Substitutionen mit trigonometrischen
Funktionen geht, versuchen wir es wieder mit dem Ansatz = sin für
2
2 und erhalten
2
?
.
1
1
1
1
was erheblich vertrauenserweckender aussieht.
=
1
1+
? $
2
2
$
.
1
einmal nicht quadratisch vorkommt, be-
+ arsinh ) +
ist, so ist
1
? $
1+
? $
Als letztes Beispiel, in dem
trachten wir noch
=
1+
2

1
2(
arcsin +
$
.
2

= 21 (sinh cosh + ) +
? $

Somit ist
h
h
2
$ cosh
h
also
1
,
2
2
1
1
was zunächst so aussieht, als sei irgend etwas falsch gelaufen. Beachtet
man aber, daß
2
1+
1
= 1
'
,

cosh + ) = cosh2 +
(
=
1
2 (sinh
2
Bei einem so komplizierten Integral empfiehlt es sich, das Ergebnis
durch Differentiation zu überprüfen; wir erhalten
Kap. 2: Mehrdimensionale Analysis
%
Hyperbelfunktionen lohnt es sich aber sicherlich, als ersten Ansatz vor
einer partiellen Integration zu schauen, ob vielleicht etwas analoges gilt
wie oben. In der Tat ist nach der Produktregel
Höhere Mathematik I SS 2007
%
3
@
3
3
@
)
@
h
h

$
%
%
*
h
*
e
)
*
h
h
*
3
)
1
2
1
2
1
,
)
h
)$
h
3
h
3
3
e
)
3
3
e
3$
3
3
e
3$
*
)$
3
3$
$
h
3$

JKJKJKJ
3
3
JK$ JKJKJ
3
h
3
e
3
3
$
e
3
e
h
h
$
3
3
3
3$
*
)
*
e
3
)
*
h
*
)$
JzJKJKJ
*
)
)$
JzJKJKJ
)
3
e
h
3
e
h
*
e
h
e
4
3
$
3
*
)
)$
*
h
e

cos
=
JK$ JKJKJ
2
1
ln
2
1+
+

1+
1
JKJKJKJ $
= ln
+
= ln

.
$
1
+
+1
.
JKJKJKJ
*
*
JK$ JKJKJ
1 tan 2
+
1 + tan 2
.
.
.

= ln
Also ist
JzJKJKJ
JzJKJzJ
3
3
Jz$ JKJzJ
1
+
+1
h
1
1
1
1
ln
2
1+
1
2
= ln
2
e
=2
e
h
1
$
Jz$ JKJKJ
=
=2
=2
h

2
2
$
sinh
e
$
Das letzte Integral kennen wir:
h
2
e
+
2
2
1+
=
2
2
$
1+
1
2 2
2
(1
)
=
(1 + 2 )2
1+
h
cos
=
Als Beispiel betrachten wir
1
Dieselbe Technik funktioniert natürlich auch bei Integralen über Hyperbelfunktionen, da man diese genausogut als Ausdrücke in Exponentialfunktionen schreiben kann. Beispielsweise ist
1
*

.
1
+
+1
$
$
+ 12 ln

=
1 tan2
1 + tan2
2
1=
3
$
cos2 (2 arctan ) =
1
$
sin(2 arctan ) =

rückgängig gemacht werden,
cos(2 arctan ) =
=
=
2
1 + tan2
2
1
.
1+ 2
Da der Arkustangens nur Werte zwischen 2 und 2 annimmt, liegt
2 arctan zwischen
und , ein Intervall, in dem der Sinus dasselbe
Vorzeichen hat wie sein Argument. Daher ist
1=
=
Nun muß nur noch die Substitution
und wir erhalten als Ergebnis
.
ist und somit
+1
1
+
+1
2
$
cos(2 ) = 2 cos ( )
$
1
3
+ ln
,
(Für komplizierte Funktionen werden wir im nächsten Abschnitt ein
Verfahren kennenlernen, daß rationale Funktionen in Summen aus einfachen Summanden zerlegt.)
1
3
=
+1
1
2
$
1
+
=1+
$
=
1
1
2
2
1
cos2
$
2
=1+
=
d.h.
1
folgt, daß
cos2
cos2
2
1
2
1
$
=
1
2
sin2
cos2
=
2
tan
$
1
2
h
und wir sind beim Integral einer rationalen Funktion angelangt. Elementare Bruchrechnung zeigt, daß
)
*
2
*
=
3
h
=
3
2
: Da sowohl 2
1
als auch 3 im Integranden vorkommen, empfiehlt sich die Substitution
= mit
=
; damit wird

2
5) Integrale der Form
(sin cos ) : Als letzte Anwendung der
Substitutionsregel in diesem Abschnitt wollen wir noch Integrale betrachten, die von trigonometrischen Funktionen abhängen. Hier führt
oft die Substitution
2
= 2 arctan
= 2
+1
zum Erfolg; sie macht sin zu sin(2 arctan ) und cos zu cos(2 arctan ),
was wir wie folgt ausrechnen können: Aus
v
h
3
%
Betrachten wir als Beispiel das Integral
Kap. 2: Mehrdimensionale Analysis
%
herleiten kann.
Höhere Mathematik I SS 2007
%
JKJKJKJ
JKJKJKJ
$
3$
JzJKJzJ
*
)
)$
JzJKJzJ
%
%
q
$
$
@
@
@
@
V V
V
.
@
)
£
1
¢
( )
¢
1(
£¤
y
r
¢
@
1(
¢
+
2
,
)
1
( )
mit linearen Polynomen , quadratischen Polynomen
und natürlichen Zahlen
. Dabei sind sowohl die als auch die paarweise
voneinander verschieden.
( )=
+
b
)
Diese Zerlegung kann algorithmisch selbst bei Polynomen mit rationalen
Koeffizienten algorithmisch sehr aufwendig sein; daher kommt der obige
Zusatz im Prinzip“ für die Durchführbarkeit der Integration rationaler
”
Funktionen.
+b
y
1

.
y
<
y
8
|
¢
b
)
k
|
¦¬
£« r
j
|
j
j
¢
ª
j
=1
} b
+
( )
j
+b
b
y
@
y
reelle Zahlen
.
+
q
$
q
q
$
$
q
y
Beginnen wir mit zwei teilerfremden Polynomen ( ) und ( ). Der
erweiterte EUKLIDische Algorithmus aus Kapitel I, 2e) liefert dazu
neue Polynome ( ) ( ), so daß
Wir müssen uns zunächst überlegen, warum das möglich ist:
=1
und
,
j
=1
¥® =1
+
+b
} b
j
©b
( )
( )
j
j
j
( )
=
( )
} b
j
läuft und
j
bzw.
©b
wobei von eins bis
sind, d.h.
+
( )
j
( )
y
und
2. Schritt: Man schreibe die Funktion ( )
lynoms und von Partialbrüchen der Form
( ) als Summe eines Po-
j
©b
j
schreiben, wobei die komplexen Zahlen die Nullstellen von sind.
Wie man sich leicht überlegt, folgt für ein reelles Polynom aus ( ) = 0
sofort, daß auch ( ) = 0 ist, d.h. die nichtreellen Nullstellen treten als
Paare konjugiert komplexer Zahlen auf, die auch jeweils die gleiche
Vielfachheit haben, da letztere über das Verschwinden von Ableitungen
definiert werden kann.
$
+b
1. Schritt: Man zerlege den Nenner in ein Produkt aus linearen und
quadratischen Polynomen. Die ist zumindest grundsätzlich möglich,
denn nach dem Fundamentalsatz der Algebra läßt sich ein Polynom
vom Grad (mir reellen oder komplexen Koeffizienten) stets in der
Form
( )= (
(
)
1 )(
2)
q
+§¦
Die Integrationstheorie rationaler Funktionen ist seit langem bekannt;
im Prinzip kann man zu jeder rationalen Funktion eine Stammfunktion
angeben, indem man wie folgt vorgeht: (Auf Einzelheiten und Beweise
muß hier weitgehend verzichtet werden, da wir nicht über das notwendige mathematische Instrumentarium verfügen.)
q
¥
wobei ( ) und ( ) Polynome sind. Es ist klar, daß diese Funktion nur
in jenen Punkten
definiert ist, in denen ( ) = 0 ist.
2
y
Unter einer rationalen Funktion versteht man eine Funktion der Form
( )
,
( )
¥a¨
Polynome vom Grad eins, zwei, drei bzw. vier heißen linear, quadratisch,
kubisch bzw. biquadratisch.
q
= deg .
2
ein quadratisches Polynom mit reellen Koeffizienten. Also läßt sich ( )
als Produkt linearer und quadratischer Polynome mit reellen Koeffizienten schreiben. Faßt man gleiche Faktoren zusammen, so erhält man
demnach eine Darstellung
=
q
als den Grad des Polynoms, in Zeichen
;
( + ) +
$
0
2
¡
= 0, so bezeichnet man
+
1
q
+
+
)=
q
=
)(
=0
(
G
( )=
ein Ausdruck der Form
G q
ist
Bekanntlich ist ein Polynom in
Das Produkt der Linearfaktoren zu zwei konjugiert komplexen Zahlen
ist
Kap. 2: Mehrdimensionale Analysis
%
i) Integration rationaler Funktionen
Höhere Mathematik I SS 2007
%
}
q
y
y
y
q
}
+
( ) ( )+ ( ) ( )=1
¯
°
¯
|
|
}
%
%
}
+
1
=
( ) ( )
¯
|
+
+
+
¯
¯
|
¯

+
²
}
¯

+
¯
±
²
±
±

¯
|
+

¯
+

¯
+
±
²

+
¯
|
¯
¯
5
1(
|
y
|
5
5
5
|
|
y
|
|
¯
5
5
¯
2
( ) +
) + ( ) 0( ) .
)+ ( ) 1 ( ) =
0(
)+
1(
0
) ( )+ 1 ( ) ( ) .
2
durch ,
2 ( ) ist nun entsprechend der Divisionsrest von 1 ( ) durch ( ) und
so weiter, bis ein Quotient ( ) kleineren Grad als ( ) hat und damit
der letzte Koeffizient +1 ( ) ist.
)+ ( )
+ V
¯
¯
|
| V
¯
¯
¯
|
¯
¢
+b
s
y
² b

+
¢
¥®
² b
¦ £«
¢
y
|
|
| V
s
y
+b
b
¢
( )
¢
£«
|
|
1
1
¢
¢
( )
+
+
+
1
1
+
£ «
£«
ª
s
r
0
+
( )
}
s ²
( )
=
( )
+
}
1
+
}
+
©
¥®
s ² b
£«
ª
¢
y
( )
1
( )
( )
1
.
1
+
( )
( )
1
1
©
0
1
Entsprechend erhalten wir die Darstellungen
+
0
( )+
+
( )
1
0
( )+
£ «
£ «
=
|
( )
=
( )
|
1
, und
+
¢
0
s
mit reellen Zahlen
( )=
1
.
Ist ( ) ein lineares Polynom, haben alle ( ) kleineren Grad als eins,
sind also Konstanten. Da deg ( ) deg
= ist, können wir also
schreiben
|
¦ =1
0(
y
£ «
=1
( )=
|
¢
¢
( )+
0(
£ «
¢
|
( )
,
( )
+
+
| V
¢
( )
+
( )
£ «
( )
=
( )
|
)
£ «
Um den Grad dieser Polynome zu reduzieren, dividieren wir für jeden
Bruch den Zähler mit Rest durch den Nenner und fassen die Quotientenpolynome zusammen zu einem einzigen Polynom ( ). Damit erhalten
wir eine neue Darstellung
y
Ist nun 1 der Quotient und 1 der Rest bei der Division von
so erhalten wir die neue Darstellung
( )=
|
+
£ «
=1
|
|
y
=1
|
( )
.
( )

y
( )
+
( )
y
y
( )
=
( )
|
+
Dies wenden wir an auf die obige Zerlegung des Nenners : Da die
( ) und die ( ) paarweise teilerfremd sind, gilt dasselbe auch für
ihre Potenzprodukte, es gibt also Polynome ( )
( ), so daß gilt

( )
|
y
)

1(
2
y
+
( ) ( )
.
( )
y
+
@
+
y
) ( )
+
1( )
) ( )+
|
+
1(
1(
y
=
)+
y
$
y
( )
0(
gibt mit deg ( ) deg ( ). (Für ein lineares Polynom ( ) =
ist das gerade die TAYLOR-Entwicklung von im Punkt .) Für 0 ( )
nehmen wir dazu den Divisionsrest von ( ) durch ( ); ist 0 ( ) der
Quotient, gilt dann
( )=
|
ist. Für ein beliebiges weiteres Polynom ist daher auch

Induktiv folgt auf diese Weise, daß es zu paarweise teilerfremden
Polynomen 1 ( )
( ) stets Polynome 1 ( )
( ) gibt, so
daß
( )
1
( )
+
= 1
+
(
(
)
(
)
)
(
)
1
1
Zur weiteren Zerlegung der Zähler überlegen wir uns zunächst, daß es
zu je zwei Polynomen ( ) und ( ) eine Darstellung
y
@
mit zwei neuen Polynomen ( ) und ( ), insgesamt also wieder eine
Summe dreier Brüche mit den drei Faktoren ( ) ( ) und ( ) als
Nennern.
s ² b
( ) kleineren Grad hat als der zugehörige
1
( )
( )
( ) ( )
( ) ( )
( )
=
+
=
+
+
( ) ( ) ( )
( ) ( )
( )
( )
( )
( )
s
( ) und
Ist ein drittes Polynom ( ) teilerfremd sowohl zu ( ) als auch zu ( ),
sind insbesondere auch ( ) ( ) und ( ) teilerfremd; es gibt also eine
Darstellung
in der jeder Zähler
Nenner.
%
( ) ( )+ ( ) ( )
( )
( )
=
+
.
( ) ( )
( )
( )
Kap. 2: Mehrdimensionale Analysis
%
ist und damit
Höhere Mathematik I SS 2007
¥ «
+
¥ «
¥«
¥«
¥ «
+
+
+b
b
%
%
Der gerade durchgeführte Beweis ist zwar (bei einer gegebenen Zerlegung des Nenners) konstruktiv, das verwendete Verfahren ist allerdings
nicht besonders effizient. Nachdem wir wissen, daß eine Zerlegung wie
oben existiert und auch alle Nenner kennen, ist es beispielsweise erheblich einfacher, von der obigen Zerlegung auszugehen (mit unbestimmten
Zählern) und die Partialbrüche nach den üblichen Regeln der Bruchrechnung zu addieren. Der Nenner des entstehenden Bruchs ist ( ), der
Zähler ( )
( ) ( ), wobei ( ) der Quotient bei der Division von
( ) durch ( ) ist. Der durch Addition der Partialbrüche berechnete
; KoeffizienZähler ist eine lineare Funktion in den Koeffizienten
tenvergleich mit ( )
( ) ( ) liefert ein lineares Gleichungssystem
für die Koeffizienten, das wir schnell und einfach nach GAUSS lösen
können.
Faßt man alles zusammen und gibt den Zählern die richtigen Indizes,
erhält man die oben angegebene Zerlegung, die sogenannte Partialbruchzerlegung.
Höhere Mathematik I SS 2007
ª
y
ª
y
$
$
y
©
} | +
ª
¢
¢
|
$
!
*
*«
y
$
!
|
$
$
y
y
*«
*
y
d.h.
+
e
~
|
j
+
( )
g
~
6
4 ³
¢
j
¢
´
( )
v
4
w
g
©
3
}
e
+
2)
=
3)
(
3
= ln
1
2)(
3
+
2
3)
.
$
=
=2
( )
+
( )
,
Bei bestimmten Integralen kann man sich gelegentlich einen Großteil
der Mühe des Ausrechnens ersparen, indem man Symmetrien berücksichtigt: Ist etwa die Funktion spiegelsymmetrisch zur Achse = ,
d.h. ( + ) = (
) für alle , für die beide Seiten definiert sind, so
ist auch
~
h
+
$
B
+
$
g
@
+
e
~
2
h
~
©
+
$
g
h
$
h
h
+
h
~ e
,
$
$
g
2
$
h
2
e
+
$
+
h
2
+
$
$
.
2
e
h
2
$
JK$ JKJzJ $
=
h
j) Symmetrie
3) (
2)(
3)
(
$
$
2)(
(
$
=
=
$
(
3
ist, folgt
1
2
$
1
$
$
+
e
$
$
JKJKJzJ
2
.
Da hier sechs das Produkt und fünf die Summe der Nullstellen des
Nenners ist, errät man leicht, daß 2 5 + 6 = (
2)(
3) ist. Die
Partialbruchzerlegung bestimmen wir nun durch probieren: Da
5 +6
$

3. Schritt: Integration der Partialbrüche: Die Integrale der Funktionen
lassen sich über die Substitution
= ( ) sofort auf
( )
zurückführen und sind somit problemlos. Weiter ist
h
2
Für Linearfaktoren ( ), die nur in der ersten Potenz vorkommen, gibt
es sogar ein noch einfacheres Verfahren: Ist die (einzige) Nullstelle
von ( ), so überlegt man sich leicht (durch Addition der Partialbrüche
und des polynomialen Anteils), daß
(
) ( )
= lim
( )
ist. Da Zähler und Nenner für = verschwinden, muß dieser Grenzwert nach DE L’HOSPITAL berechnet werden; wir erhalten
(
) ( )
( )
( )
= lim
=
,
( )
( )
wobei hier der Nenner nicht verschwinden kann, da nur eine einfache
Nullstelle von ist.
k
Als ganz einfaches Beispiel, in dem alles explizit durchführbar ist, betrachten wir
Bleiben schließlich noch die Integrale mit Potenzen eines quadratischen
Polynoms im Nenner; hier wird durch partielle Integration rekursiv
erniedrigt.
wobei das erste Integral nach der Regel über die logarithmische Ableitung aus Abschnitt a) berechnet werden kann, während wir das zweite
in Abschnitt b) behandelt haben.
Kap. 2: Mehrdimensionale Analysis
%
e
~
e
g
~
B
e
@
B
e
@
}
@
B
@
Höhere Mathematik I SS 2007
%
=
$
und
g
~
g
~
e
( )
( )
= 0,
h
h
h
e
$
~ e
$
~
g
~
g
~
h
G e
G
sin
nicht durch elementare
Tatsächlich ist die Stammfunktion von
transzendenten Funktionen wie die Exponentialfunktion, die trigonometrischen Funktionen sowie deren Umkehrfunktionen und/oder Wurzeln und Grundrechenarten darstellbar, und sie teilt diese Eigenschaft
mit einer ganzen Reihe weiterer Stammfunktionen.
k) Einige nicht elementar integrierbare Funktionen
4
x 8
10
Abb. 64: Der Integralsinus
6
2
12
14
2
.
h
?

)
!"
(Der Vorfaktor sorgt dafür, daß lim
Erf( ) = 1 ist, was wir im
Augenblick allerdings noch nicht beweisen können.)
0
*e
2
)
Erf( ) =
hat keine elementar
2) Die Fehlerfunktion: Auch die Funktion
angebbare Stammfunktion; hier definiert man als eine Stammfunktion
die Fehlerfunktion oder error function durch
2
*
Sie ist wichtig für die Statistik, denn für eine normalverteilte Zufallsvariable (dazu gehören die meisten Meßgrößen) mit Mittelwert und
*
Einige wichtige dieser neuen Funktionen sind
8
00
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
*
Da einige dieser Stammfunktionen trotzdem für Anwendungen wichtig
sind, behilft man sich damit, daß man einigen speziellen dieser Funktionen Namen gibt und versucht, alles darauf zurückzuführen. Die so
definierten Funktionen können dann, genau wie der Sinus und die Exponentialfunktion, in Tabellenwerke und Unterprogrammbibliotheken
aufgenommen werden, so daß man mit den dadurch abgedeckten Integralen genauso rechnen kann wie mit den elementaren transzendenten
Funktionen.
<
aber ein Leser, der mit den uns bislang bekannten Methoden nach einer
Stammfunktion suchen möchte, dürfte eine sehr harte Zeit und wenig
Erfolg haben.
1
*fe
= 0,
sin( )
für alle
wohldefiniert und eine stetige Funktion von , der Integralsinus. Anwendungen finder er beispielsweise in der Elektortechnik,
wo man für gewisse Filter Faltungsintegrale mit sin benötigt.
0
sin
= 1 ist, ist das bestimmte Integral
*
1
!
Si( ) =
( )
sin
h
ohne daß man irgendetwas über die Stammfunktion von wissen müßte.
So ist beispielsweise
+

+
0
1) Der Integralsinus: Da lim
Viel interessanter wird es, wenn punktsymmetrisch zu einem Punkt
(
). Dann ist
( 0) auf der -Achse ist, d.h. ( + ) =
Kap. 2: Mehrdimensionale Analysis
%
@
%
µ
h
*
e
,
*
¶
)
g
?

@
$
$
$
$

&
@
=
g
JKJzJKJ
$
g
h
"
h
e
e
?
r
B
def
=
1
1
1
1
1
1
1
für

$
g
&

1
1
.
1.
Auch wenn wir nicht bis unendlich integrieren wollen, gibt es Beispiele
von Integralen, denen wir via Grenzwertbetrachtung einen sinnvollen
1
r
sin2
r
$
2

&
h

@
h
e
1
1
@
oder
e
sin2
w
h
$ r
B
2
1
1)
=1

1
(
r
,
+ 2+ +
wobei das Polynom im Nenner keine mehrfachen Nullstellen hat, oder
auf Integrale der Form
B
=
. Dann ist für eine reelle Zahl
@
r
3
0 und
@
Falls
1 ist, können wir hiervon den Grenzwert für gegen unendlich
betrachten und es liegt nahe, diesen als Wert des Integrals von bis
unendlich zu bezeichnen:
Sei
l) Uneigentliche Integrale
&
w
B
3) Elliptische Integrale: Bei der Berechnung der Bogenlänge eines
Ellipsensegments kommt man, je nach Art des Ansatzes und der Substitution, auf Integrale der Form
2
4) Algebraische Integrale: Die erste Form der elliptischen Integrale ist
ein Spezialfall eines sogenannen algebraischen Integrals; das sind Integrale, deren Integranden durch Wurzeln und Grundrechenarten (oder
allgemeiner implizit durch Lösungen von Polynomgleichungen) gegeben sind. Die komplizierteren dieser Integrale sind fast alle nicht elementar ausdrückbar; es gibt inzwischen algorithmische Verfahren, die
entscheiden, wann ein solches Integral elementar ausdrückbar ist, und
die dann auch eine Stammfunktion finden können. Natürlich gibt es
auch hier spezielle Funktionen, mit denen sich weitere dieser Integrale
ausdrücken lassen.
.
-1
.
Abb. 65: Die Fehlerfunktion
µ
-0.5
x1
µ
00
-1
B
-2

2
2
0.5
1
1
Erf
2
?
2
2

1
Erf
2
ein Integral, von dem man sich leicht überlegt, daß es mit Hilfe von Erf
berechnet werden kann als
B
w
2
k
1
2
mit 0
1. Alle diese Integrale heißen elliptische Integrale und
sind nicht elementar ausdrückbar. Eine hauptsächlich auf ADRIEN MARIE LEGENDRE (1752–1833) und KARL THEODOR WILHELM WEIERSTRASS (1815–1897) zurückgehende Theorie der elliptischen Funktionen stellt das Instrumentarium bereit, mit dem man diese vor allem in
der Geodäsie, Kartographie und im Maschinenbau wichtigen Integrale
berechnen kann.
Kap. 2: Mehrdimensionale Analysis
%
1
2
Standardabweichung ist die Wahrscheinlichkeit dafür, daß ein Meßwert zwischen und liegt, gleich
Höhere Mathematik I SS 2007
%
k
e
$
k
? $
%
B
m

=
r
~
@
B
B
B
h
~ e

$
@

$
B
$
$
B
r
$
$
g
Jz
r JKJKJ
$
r
g
B
B
B
@
&
1
G
:
w !
*
A
&
&
F
B
A
B
$
A
F
B
$
G :
A
B
A
$
GB
G $
:
!
g
*
A
&
&
F
A
B
G
B
F
G :
$
¸
B
·
B
@
+
= lim
( )
,
sei
;
In diesem Fall läßt sich das Intervall so in Teilintervalle zerlegen, daß
in jedem Teilintervall höchstens an einem der beiden Intervallenden
uneigentlich ist: Falls es keine Undefiniertheitsstellen im Intervallinnern
gibt, wählen wir willkürlich ein 0 zwischen und und betrachten
die beiden Intervalle ( ] und [ ). Im anderen Fall können zwei
Zusatzpunkte notwendig sein: ein Punkt 0 zwischen und 1 sowie ein
Punkt +1 zwischen und .
@
<
¹
m
@
JKJ
<
8
B
m
@
JKJ
<
8
·
¹
2 @
B
B
.
)=
,
Diese Definitionen sind immer noch nicht allgemein genug: Eine Funktion könnte auch an beiden Enden eines Intervalls ( ) undefiniert
sein, wobei wir auch die Sonderfälle =
und/oder =
zulassen wollen, und zusätzlich könnte sie auch noch Undefiniertheitsstellen
im Intervallinnern haben.
1
r
$
und (
.
falls dieser Grenzwert existiert; andernfalls sagen wir, das Integral sei
divergent.
g
B
def
( )
$
] =
e
B
(
w
~
@
entsprechend auch
( )
Völlig analog definieren wir linksseitige uneigentliche Integrale:
stückweise stetig auf dem halboffenen Intervall ( ] mit
dann ist
h
!
~
;
= lim
g
def
=
falls dieser Grenzwert existiert; andernfalls sagen wir, das Integral sei
divergent.
g
e
2
) =
2
[
e
w
B
auch für unendliche definiert sein sollen durch
( )
h
h
)=
~
w !
~
@
[
!"
w
g
@
B
Schließlich sollten wir, wenn wir schon beim Definieren sind, zur Bezeichnungsökonomie noch vereinbaren, daß halboffene Intervalle wie
@
~ e
B
0 gibt,
B
@
0 ein
B
h
8
definieren durch die Bedingung, daß es für jedes
für alle mit
+ .
so daß ( )
8
<º $
( )
*
Mit all diesen Definitionen können wir dann eine Funktion betrachten,
die in einem halboffenen Intervall [ ) mit
definiert und
stückweise stetig ist; für diese definieren wir das rechtsseitig uneigentliche Integral
<º
2
+
!
2
¹
= lim
g
»
»
Völlig analog läßt sich natürlich auch ein rechtsseitiger Grenzwert
2
( ) für
¹
wenn es für jedes
0 ein
0 gibt, so daß ( )
für alle
mit
. (Zur Erinnerung: Beim gewöhnlichen Grenzwert
fordert man dies für alle mit
, d.h.
+ .)
w !
~
( ),
g
Grenzwert lim stehen soll; entsprechend bei lim
+
für den gewöhnlichen
$
= lim
( )
2
und auch hier liegt es nahe, den Grenzwert für
als Wert des
Integrals von bis zu bezeichnen. Wir müssen hier allerdings vorsichtig
sein mit dem Grenzübergang, denn die obige Formel gilt natürlich nur für
; für
ist das Integral undefiniert. In einer solchen Situation
können wir daher nicht den gewöhnlichen Limes betrachten, sondern
brauchen einen eingeschränkten Grenzwertbegriff, der nur Folgen von
einer der beiden Seiten berücksichtigt: Allgemein schreiben wir
,
der Ausdruck lim
v
=
her, daß für =
)
)1
1
@
(
(
B
)1
1
(
~
)1
1
h
(
Für unendliche Intervallgrenzen sind die Definitionen für links- und
rechtsseitige Grenzwerte nicht sinnvoll anwendbar; wir vereinbaren da-
Kap. 2: Mehrdimensionale Analysis
%
Wert zuordnen können, ohne daß das Integral im Sinne unserer bisheriund
gen Definitionen existieren würde: Beispielsweise ist für
eine relle Zahl 0
1
Höhere Mathematik I SS 2007
@
@
B
r
r
2 2
m
JKJ
<
8
·
2
$
%
~ e
~ e
e
~¤
g
5
5
5
h
~
h
g
B
konvergiert; die Summe ihrer Werte bezeichnen wir als den Wert des
Integrals von bis .
+1
( )
h
0
w
( )
konvergiere, wenn
( )
v
1
0
h
jedes der Integrale
w
( )
@
"
h
e
2
"
<
"
=
h
h
e
e
=2
0
1+
$
"
"
arctan 0) =
2
h
~ e
!"
~
!"
~
.
h
3
e
$
2
2
w

!
º
h
h
h
v
existiert, bezeichnen wir ihn als CAUCHYschen Hauptwert von
( )
nach dem aus der Analysis I bekannten französischen Mathematiker
g
e
2
3
3
=
32 32
e
~
=0+
h
3
~

+
3
=
( )
h
3

e
4
+
w
( )
2
0
h
4
@
lim
Da somit alles von der Anwendung abhängt, kann die Mathematik hier
nicht mehr bieten als eine Definition: Falls für die Funktion , die auf
[ ) ( ] definiert ist, der Grenzwert
B
könnte man etwa argumentieren, daß der Integrand eine ungerade Funktion ist, so daß aus Symmetriegründen das Integral von 2 bis 2 verschwinden sollte und
2
4
Obige Forderung, daß jedes der Teilintegrale einzeln konvergieren soll,
ist gelegentlich etwas sehr restriktiv. Für das bei Null uneigentliche
Integral
= 2( lim arctan
2
2
1+
1+
e
0
"
0
h
= 2 lim
+
e
2
"
1+
2
h
1+
Entsprechend gibt es durchaus Situationen, in denen das mathematische Modell einen unendlich großen Wert vorhersagt, wohingegen in
der Realität limitierende Faktoren, die für Werte im üblichen“ Größen”
bereich noch keine nennenswerte Rolle spielen, für eine Begrenzung
sorgen. Falls man in einer solchen Situation sicher sein kann, daß auch
in der realen Situation noch die Symmetrie zum Nullpunkt erhalten
bleibt, kann man so wie oben argumentieren; falls allerdings die Symmetrie nicht erhalten bleibt, können durch die Begrenzung der Funktion
beliebig große Abweichungen erzeugt werden, über die man mit dem
vereinfachten mathematischen Modell nichts aussagen kann.
¼
0
Da der Integrand eine gerade Funktion ist, empfiehlt es sich, das Integrationsintervall, das hier aus ganz besteht, bei Null zu unterteilen,
und wir erhalten
.
$
Andererseits sind aber viele der mathematischen Formeln, die in den
Naturwissenschaften und der Technik angewandt werden, nur näherungsweise gültig: Mathematische Modelle sind praktisch immer vereinfachende Modelle der Wirklichkeit, beispielsweite gilt das OHMsche
Gesetz sicher nicht mehr, wenn man einen 5 -Widerstand aus einer
auf 5 V Spannung ausgelegten Schaltung im Hochspannungslabor mit
100 kV belastet, und es gilt auch nicht mehr ohne Korrekturterme, wenn
man einen Wechselspannung mit 500 MHz anlegt.
1+
Als Beispiel betrachten wir das an beiden Grenzen uneigentliche Integral
1
sein sollte. Diese Art der Argumentation ist durch das, was wir bislang
gelernt haben, nicht gedeckt, und es gibt auch gute Gründe, sie zu ver0 gegen
bieten: Schließlich geht die Stammfunktion 12 2 für
minus unendlich, und wenn eine Größe mit Relevanz in der realen Welt
unendlich groß wird, hat dies im Allgemeinen zu gravierende Konsequenzen, als daß man einfach durch diesen Punkt hindurch weitergehen
könnte.
Kap. 2: Mehrdimensionale Analysis
%
Wir sagen dann, das uneigentliche Integral
Höhere Mathematik I SS 2007
g
e
e
%
w
e

$
B
B
@
@
h
$
B
g
m
$
$
m
@
h
$
2
°
0
1
für
0
= 1.
= lim
(
1
1)
1
.
= lim
0
=
1
1
1
existiert ein Grenzwert genau dann, wenn
1 ist; alsdann ist
=
.
Zusammen mit der Monotonieeigenschaft des RIEMANN-Integrals aus
3a) ergeben sich hieraus zwei allgemeine Kriterien für die Konvergenz
uneigentlicher Integrale:

y
h
;
"v
½
¾
m
G
G
Satz: Die Funktion sei stetig für
und sei stetig für 0
.
Dann gilt:
1.) Falls es eine reelle Zahl
und eine reelle Zahl
1 gibt, so daß
( )
ist, konvergiert
( ) .
2.) Falls es eine reelle Zahl und eine reelle Zahl 0
1 gibt, so
ist, konvergiert 0 ( ) .
daß ( )
B
$
$
$
JKJzJKJ e
führen, und natürlich ist keine Anwendung denkbar, in der eine negative
Zahl in sinnvoller Weise als Integral über eine überall positive Funktion angesehen werden kann. In der Tat existiert im obigen Beispiel
weder das Integral noch dessen CAUCHYscher Hauptwert, da sich die
Unendlichkeiten links und rechts der Null hier nicht wegheben, sondern
verstärken.
B
1
$
&
e
2
&
r
!g
1
=
2

@
g
1
2
@
g
w
h
e
=
&
e
12
r
2

"
r
!"
w
2
&
h
0 und
0, also
B
w
g
h
$
1
g
12
e

=
existiert ein Grenzwert genau dann, wenn
1 ist; alsdann ist
$
0 und
0, also

r
B
2
r
w
1
e
h
1
(1
1
)
JKJKJKJ
h
$
r
setzt, wobei eine zwar in den Punkten und , nicht aber auch für
definierte Stammfunktion von ist: So
jeden Zwischenwert
etwas kann zu Ergebnissen wie
r
g

Für
r
w
=
@
( )

( )

&
r
=
Für
r

( )

.
Der CAUCHYsche Hauptwert darf auch nie als eine Rechtfertigung dafür
verstanden werden, daß man unbesonnen

Zu einer etwas systematischeren Untersuchung uneigentlicher Integrale empfiehlt es sich, zunächst die Potenzen zu betrachten. Für positiüberall definiert, so daß Integrale über einen
ve Exponenten ist
endlichen Bereich unproblematisch sind; für Integrale über einen unendlichen Bereich rechnet man leicht nach, daß sie immer divergieren.
Für = 0 ändert sich nichts an dieser Situation; interessant ist also nur
der Fall
0, wo sowohl der Wert = 0 als auch unendliche obere
und/oder untere Grenzen zu Problemen führen können. Für negatives
ist
=1
, wir interessieren uns also für
Kap. 2: Mehrdimensionale Analysis
r
Die Frage, wann der CAUCHYsche Hauptwert für ein eigentlich divergentes Integral verwendet werden sollte, ist keine mathematische Frage: Unter rein mathematischen Gesichtspunkten gibt es nie eine Rechtfertigung
für die Verwendung des CAUCHYschen Hauptwerts. Der CAUCHYsche
Hauptwert ist nur dann sinnvoll anwendbar, wenn man davon ausgeht,
daß ein mathematisches Modell eine Situation nur für nicht zu große
Funktionswerte (ungefähr) korrekt beschreibt, und wenn man gleichzeitig sicher ist, daß die Unendlichkeitsstelle des mathematischen Modells
für die Anwendung unproblematisch ist und gleichzeitig die Symmetrie,
die der Berechnung des CAUCHYschen Hauptwerts zugrundeliegt, auch
in der realen Anwendung gilt.
Baron AUGUSTIN LOUIS CAUCHY (1789–1857). Entsprechend reden wir
auch in komplizierteren Situationen mit mehreren Unstetigkeitsstellen
vom CAUCHYschen Hauptwert, falls sich eine Aufteilung in Teilintervalle finden läßt, so daß für jedes Teilintervall der CAUCHYsche Hauptwert
3
existiert. Im obigen Beispiel wäre also 32
der CAUCHYsche Hauptwert
des Integrals, wohingegen das Integral selbst undefiniert ist.
Höhere Mathematik I SS 2007
%
m
@

h
w
g
*¤
G
v
y
½
¾
m
*¤
G
y
%
Beweis: 1.) Nach der Monotonieregel ist für jedes
Höhere Mathematik I SS 2007
w
w
h
e G
@
B
r
e
h
G
½
m
g
g
B
B
G
G
¾
*¤
"
Á
h
"
e
Z
Z
¿ U ³À $
)
h
G
e G
G
h
G
@
2
@
g
g
,
2
4
0
3
1
.
3
r
m
*
"
oder
1+
@
*
½
)$
e
.
+3
½
;
r
m
,
+3
1
und (beispielsweise) = 2, da die
und dies gilt mit geeignetem
Exponentialfunktion schneller wächst als jedes Polynom.
1
1
Diese Ungleichung ist äquivalent zu
für alle
Letzteres Integral existiert nach dem gerade bewiesenen Satz, wenn wir
finden können, so daß

½ ½
*
h
½
@
)$
Z
Z
Entsprechend gilt für 0
1 die Ungleichung etwa mit = 12 ,
1 stärker wächst als jede -Potenz. Also konvergiert das
da dort
Integral sowohl an seiner unteren als auch seiner oberen Grenze, und
)
*
Die Abhilfe besteht bekanntlich darin, daß man die Gleichverteilung
der Frequenzen durch eine BOSE-EINSTEIN-Statistik ersetzt und als neue
r
0
8

einem offensichtlich divergenten Integral: Das ist die sogenannte UV”
Katastrophe“, die dieses Modell zum Widerspruch führt.

0
1
=
erhalten wir

,
1
Á
;
2
"
e
)$
Dieses Integral ist an beiden Grenzen uneigentlich; betrachten wir also
eine positive Konstante und getrennt die Integrale von 0 bis und von
bis .
2
3
e
8
=
Mit der Substitution
k
*
@
Als Beispiel hierfür betrachten wir die Strahlung eines schwarzen
Körpers: Nach dem RAYLEIGHschen Strahlungsgesetz, wonach alle mit
der Geometrie des Körpers verträglichen Wellenzahlvektoren gleichwahrscheinlich sind, wäre die Energiedichte proportional zum Quadrat
der Frequenz, die Gesamtenergie also proportional zu
0
3
2.) geht völlig analog.

Z
und damit auch das gesuchte Integral als ihre Differenz.

,
2

und die UV-Katastrophe wird genau dann vermieden, wenn dieses Integral konvergiert.
8
e
k
( )
"
¿ U ³À $
)
und
¿ U ³À $
)
Z
"
( )

h
Z
h
( )+
Á
Genau dasselbe gilt für die ebenfalls nichtnegative Funktion ( )+ ( ) ,
die durch 2 beschränkt ist; also existieren die uneigentlichen Integrale
k
1
erhält, wobei das PLANCKsche Wirkungsquantum, die BOLTZMANNKonstante, die Lichtgeschwindigkeit und die absolute Temperatur
bezeichnet. Hier ist die Gesamtenergie
2
3
Z
und letzteres Integral konvergiert, wie wir gerade nachgerechnet haben,
unter den angenommenen Voraussetzungen. Das linksstehende Integral
ist somit beschränkt durch eine von unabhängige Konstante; da es wegen der Nichtnegativität des Betrags zusätzlich eine monoton wachsende
Funktion von ist, existiert daher der Grenzwert nach dem bekannten,
schon für die Existenz des RIEMANN-Integrals verwendeten Satz aus der
Analysis I, wonach jede monotone und beschränkte Folge reeller Zahlen
konvergent ist.
,
( )
;
8
Energiedichte nun nach dem PLANCKschen Strahlungsgesetz
Kap. 2: Mehrdimensionale Analysis
%

m
m
)$
%
"
&
h
*

e
)
Â
=
)
1
mit
0
1,
$
*
m

*
)

*
+
*
r
;

*
)
-
Ã
½
r
m
)
1
0 definierte Funktion
( ) heißt EULERsche
1
2
Ä
h
)
Â
Â
1

&
e
Â
=
" JKJzJKJ

)
h
0
=1
4
=
( + 1)
Â
$
h
Â
$
)
5
ergibt sich somit, daß für alle natürliche Zahlen gilt ( ) = (
1)! ;
die -Funktion ist also eine Art stetig gemachter Fakultätsfunktion.
GAUSS definierte auf andere Weise eine stetige Funktion Π( ), für die
Π( ) = ! ist, aber wie sich bald herausstellte, ist Π( ) = ( +1), so daß
nur eine der beiden Funktionen wirklich gebraucht wird. Nach einigen
Modewechseln im letzten Jahrhundert entscheidet man sich heute meist
0
"

(1) =
Abb. 66: Die -Funktion
3
x
)
Aus dem elementar berechenbaren Wert
2
4
6
8
10
12
14
16
18
20
22
24
( ).
0
LEONHARD EULER (1707–1783) wurde in Basel geboren und ging auch dort zur Schule und, im Alter von 14
Jahren, zur Universität. Dort legte er zwei Jahre später
die Magisterprüfung in Philosophie ab und begann mit
dem Studium der Theologie; daneben hatte er sich seit
Beginn seines Studium unter Anleitung von JOHANN
BERNOULLI mit Mathematik beschäftigt. 1726 beendete
er sein Studium in Basel und bekam eine Stelle an der
Petersburger Akademie der Wissenschaften, die er 1727
antrat. Auf Einladung FRIEDRICHS DES GROSSEN wechselte er 1741 an die preußische Akademie der Wissenschaften; nachdem sich das Verhältnis zwischen den
beiden dramatisch verschlechtert hatte, kehrte er 1766 nach St. Petersburg zurück. Im gleichen Jahr erblindete er vollständig; trotzdem schrieb er rund die Hälfte seiner zahlreichen
Arbeiten (73 Bände) danach. Sie enthalten bedeutende Beiträge zu vielen Gebieten der
Mathematik, Physik, Astronomie und Kartographie.
Die somit für alle
Gamma-Funktion.
folgt wieder, da die Exponentialfunktion stärker wächst als jede Potenz.
1
Auch die obere Grenze ist unproblematisch, denn die dazu notwendige
Abschätzung
1
1
1
1 ist
so daß obiger Satz sofort die Konvergenz zeigt.
1
Diese untere Grenze ist völlig harmlos, denn für 0
Â
( + 1) =
Â
betrachtet. Dieses Integral ist natürlich immer uneigentlich an der oberen
Grenze; für
1 zusätzlich auch noch an der unteren.
oder
0
" JKJzJKJ
*

)
0
*
def
e
0
1
e
0

*
für
+

1
=
( ) =
"
1
Â
( )=
"
Als (vorerst) letztes Beispiel eines uneigentlichen Integrals sei noch
Die wichtigste Eigenschaft der -Funktion folgt durch partielle Integration:
Kap. 2: Mehrdimensionale Analysis
%
dazwischen ist ohnehin alles unproblematisch, da der Integrand stetig
ist.
Höhere Mathematik I SS 2007
%
Â
Â
%
Â
<
<
©
B
<
1
@
©
<
©
B
1
©
@
©
r
5
5
5
$
©
<
5
5
5
@
©
©
B
1 : [0
2 ]
©
©
@
r
r
©
1]
2
;
1

1
(cos 2
sin 2 )
(cos sin ) ,
<
;
2

1
©
2
<
;
2

3:
$
2
1
+1
2
+1
2
eine Möglichkeit. Es geht aber auch ganz anders, denn auch bei
2 : [0
aber natürlich wäre auch
1
Die Bedingung im Teil b) der obigen Definition stellt sicher, daß Kurven, anschaulich betrachtet, zusammenhängend sind; es hat allein praktische Gründe, daß man nicht auch von den Intervallen verlangt, daß
sie unmittelbar aneinander anschließen: Oft werden die Formeln für ein
Kurvenstück einfacher, wenn man einen bestimmten Anfangswert wie
etwa die Null für das Intervall nehmen kann.
1 ( 1 ) ist.
( )=
heißt geschlossen, wenn
1.
:
Anschaulich kann man sich ein Kurvenstück durch sein Bild im
vorstellen, allerdings muß man beachten, daß dasselbe Bild durch ganz
verschiedene Funktionen parametrisiert werden kann. Als Beispiel für
verschiedene Parametrisierungen einer und derselben Kurve betrachten
wir den Einheitskreis 2 + 2 = 1. Seine bekannteste Darstellung als
Kurvenstück ist die Parametrisierung
<
c) Eine Kurve
B
für = 1
+1 )
Å©
+1 (
.
Man beachte, daß für die Intervallendpunkte nichts gefordert wird:
Selbst wenn die Ableitung dort existiert, muß sie nicht von Null verschieden kann. Auf diese Weise läßt sich ein Kurvenstück, bei dem ( )
an endlich vielen Stellen gleich dem Nullvektor ist, immer noch als
stückweise reguläre Kurve auffassen.
©
( )=
8
von Kurvenstücken mit der Eigenschaft, daß
©
@
]
B
<
:[
1
©
1
<
Definition: a) Ein Kurvenstück : [ ]
heißt regulär, wenn
( ) = 0 für alle
( ).
b) Eine Kurve heißt stückweise regulär, wenn sie aus regulären Kurvenstücken zusammengesetzt werden kann.
Å©
Å©
eines Intervalls in den
.
b) Eine Kurve ist eine endliche Folge von Kurvenstücken
@
]
©
B
1
ist eine stetig differenzierbare Abbil-
©
<
Definition: a) Ein Kurvenstück
dung
:[
a) Kurven und Tangentenvektoren
@
Bislang haben wir nur Funktionen einer Veränderlichen über ein Intervall integriert. Als ersten Schritt ins Mehrdimensionale wollen wir
nun Funktionen mehrerer Veränderlicher betrachten und diese entlang
integrieren. Entsprechende Integrale benötigt man
einer Kurve im
einerseits, um Bogenlängen von Kurven zu berechnen, vor allem aber
sind sie wichtig, um die aufzuwendende oder freiwerdende Energie bei
der Bewegung eines Objekts in einem Kraftfeld (oder einem elektrisch
geladenen Teilchens in einem elektrischen Feld usw.) zu berechnen. Wir
beginnen mit der Definition von Kurven:
B
§4: Kurvenintegrale im
Ein wesentlicher Unterschied zwischen einer Kurve und einem Kurvenstück liegt in der Differenzierbarkeit: Durch Verschiebung der Parameterintervalle könnte man jede Kurve durch eine stetige Abbildung
:[ ]
beschreiben, aber dort, wo zwei Kurvenstücke aneinanderstoßen, muß diese Abbildung nicht differenzierbar sein; anschaulich
gesprochen kann die Kurve dort einen Knick“ haben.
”
Die Ableitung ( ) ist ein Vektor, dessen Komponenten die Ableitungen der Koordinatenfunktionen von ( ) sind; wir bezeichnen ihn als
Tangentenvektor der Kurve im Punkt ( ). Gelegentlich wird es wichtig
sein, daß dieser Vektor ungleich dem Nullvektor ist; wir definieren daher
Kap. 2: Mehrdimensionale Analysis
%
für ( ): Diese Funktionswerte sind in Tafelwerken tabelliert, und numerische Verfahren für ihre Berechnung stehen in den einschlägigen Unterprogrammbibliotheken und Computeralgebrasystemen zur Verfügung.
Höhere Mathematik I SS 2007

<
1
©
%
L
1
©
<
©
Æ
Abb. 67: Graph der Funktionen ( ) =
-1
1
4
und ( ) = 22+1
Æ

Ç
$
Å©
©
:
$
$
Å©
©
:
2
+1
$ ©
$
$ $
$ ©
$
$ +1
Ë
+1
Å©
2
Ê
=
©
Å©
(
$
2
2
Ê
1
Å©
2
( 2 + 1)2
+1 )
)=
) schließlich zeigt eine kurze Rechnung, daß
©
( )
Í
3(
$
3(
:
:
)=
©
,
©
2
2
und wählen in jedem Teilintervall (
+1 ) einen Zwischenpunkt . Der
Tangentenvektor im Punkt ist nach Definition ( ), allerdings ist das
nicht unbedingt der Vektor, den wir wollen: Wir wollen schließlich die
Kurve durch ihre Tangente annähern, und dazu müssen wir die Länge an
das Intervall anpassen, über dem wir die Kurve approximieren wollen.
Indem wir den Vektor ( ) der Differentialquotienten durch
1 ( +1 )
1( )
1
1
..
( ) ( +1 ) =
.
@
=
2 sin 2
2 cos 2
Ê
und für (
:
)=
@
2(
1
) ist
2(
)=
B
<
für (
,
=
sin
cos
ÉÈ
ein Kurvenstück; wir unterteilen das Intervall,
Sei also : [ ]
wie wir es vom RIEMANN-Integral her gewohnt sind, durch Zwischenpunkte
= 0
=
1
1
ÉÈ
)=
Nichts spricht dagegen, bei der Definition der Bogenlänge genauso vorzugehen: Die primitiven Bausteine, mit denen wir die Kurve annähern,
sind nun natürlich keine Rechtecke mehr, sondern Strecken; am einfachsten nehmen wir dazu Tangentenvektoren. Dazu brauchen wir allerdings
Differenzierbarkeit, wir müssen uns also zunächst auf ein Kurvenstück
beschränken.
B
1(
Jede dieser Parametrisierungen führt zu anderen Tangentenvektoren:
Für einen festen Kurvenpunkt liegen zwar alle drei Vektoren auf ein
und derselben Geraden, der Tangenten an den Kreis, aber sie haben
) = 1 ( ) ist
verschiedene Länge: Für (
P
2 +1
2
t
©
-0.5
2
©
0
©
In der Integralrechnung wird die Fläche unterhalb einer Kurve dadurch
definiert, daß man sie durch Rechtecke angenähert; falls deren Gesamtfläche bei immer feiner werdenden Unterteilungen gegen einen festen
Grenzwert konvergiert, bezeichnetet man diesen als Fläche unterhalb der
Kurve oder auch als RIEMANN-Integral über die die Kurve beschreibende
Funktion.
©
-2
©
-4
b) Die Bogenlänge einer Kurve
©
0.5
©
1
ist. Bei der Parametrisierung mit 2 sind die Tangentenvektoren also
jeweils 2 mal so lang wie bei der mit 1 , was man anschaulich so
interpretieren kann, daß der Kreis bei dieser Parametrisierung 2 mal so
schnell durchlaufen wird wie bei der mit 1 . Bei der Parametrisierung
mit 3 ist die Länge der Vektoren variabel, und sie zeigen auch in
die Gegenrichtung zu den Tangentenvektoren an 1 und 2 ; bei dieser
Parametrisierung wird der Kreis also im Uhrzeigersinn durchlaufen.
Kap. 2: Mehrdimensionale Analysis
%
liegen sämtliche Bildpunkte auf dem Einheitskreis, und zumindest für
jedes endliche Teilintervall von definiert auch 3 ein Kurvenstück.
Wie eine kurze Kurvendiskussion (oder ein Blick auf Abbildung 67)
zeigt, besteht das Bild von 3 aus allen Punkten des Einheitskreises
.
außer (1 0); letzterer Punkt ist der Grenzwert von 3 ( ) für
Höhere Mathematik I SS 2007
Ê
Î
©
Ì
:
$
©
$
1
$
$
$
Höhere Mathematik I SS 2007
%
$
$
$
$ ©
$ $
$ ©
( ) (
)
$
Ê
ungefähr gleich
È
( )
(
$
).

1
JKJ
Ê
Å©
JKJ
h
JKJ
Å©
J J
e K
©
©
5
5
]
ist
b) Die Bogenlänge einer Kurve , bestehend aus den Kurvenstücken
ist die Summe der Bogenlängen der Kurvenstücke .
1
g
r
5
Hier ist
1(
©
$
Å©
©
)
=
0
Å©
JKJ
JKJ
Å©
J J
K
1(
JKJ
= e
0
sin2 + cos2 = 1 ,
=2 ,
) =
(cos sin ) .
1
2
1(

und damit ist die Bogenlänge
;
?
2
1
also
2
<
sin
cos
2 ]
)=
1 : [0
Um zu sehen, ob das alles wirklich vernünftig ist, berechnen wir die
Bogenlänge der Kreislinie
©
nach Definition eines Kurvenstücks stetig differenzierbar ist,
Da
ist auch ( ) immerhin noch eine stetige und damit insbesondere
RIEMANN-integrierbare Funktion; wir wissen also, daß der Grenzwert
für immer enger werdende Verfeinerungen der Unterteilung existiert
und gleich dem Integral über diese Funktion ist. Somit kommen wir auf
ganz natürliche Weise auf die
.
©
-1
1
w
()
Definition: a) Die Bogenlänge eines Kurvenstücks : [
©
-0.5
0.5
1
@
0
0.5
1
-0.5
-1
-0.5
0
B
0.5
-0.5
Abb. 69: Bogenlänge des Einheitskreises angenähert durch fünfzig Strecken
-1
0.5
1
<
Abb. 68: Bogenlänge des Einheitskreises angenähert durch zwanzig Strecken
-1
1
Für die Kreislinie mit ihrer Parametrisierung
(cos sin ) ist dies in
den Abbildungen 68 und 69 dargestellt für eine äquidistante Unterteilung
des Intervalls [0 2 ] in zwanzig bzw. fünfzig Teilintervalle; im letzteren
Fall ist in der Tat kaum mehr ein Unterschied zu sehen zwischen der
Kreislinie und den fünfzig Vektoren, durch die sie approximiert wird.
+1
=0
1
ist, die Bogenlänge der Kurve kann also angenähert werden durch
Å©
+1
+1 )
1
approximieren sehen wir, daß der Vektor ( ) (
Kap. 2: Mehrdimensionale Analysis
%
h
h
JKJ
Å©
= e JKJ
%
$
1

1
<
©
©
;
"
3(
JzJ
e
Å©
JzJ
"

h
$
$
4
( + 1)2
2
$
h
h
h
$

Å©
JKJ
$
JKJ
$
"
=2 ;
2
4(
Å©
JKJ
$
2
e
=2
;
)
=
h
JKJ
= 2 arctan
2
0
20
= 20 .
(cos sin )
h
Wir müssen also etwas sorgfältig sein, wenn wir präzisieren wollen, was
die Unabhängigkeit der Bogenlänge von der Parametrisierung wirklich
bedeuten soll; da das ganze dadurch auch etwas umfangreicher wird, sei
das entsprechende Lemma in den nächsten Abschnitt verschoben, wo
wir es gleich etwas allgemeiner beweisen werden.
Auch das erscheint geometrisch durchaus sinnvoll: Wenn man nicht nur
einmal, sondern zehnmal im Kreise herum geht, legt man schließlich
einen zehnmal so langen Weg zurück.
0
20
=
e
h
+1
20 ]
die Kreislinie, aber nun ist die Bogenlänge
4 : [0
Ganz so einfach ist die Sache allerdings nun doch nicht: Schließlich
parametrisiert auch
=
2
1
auch bei dieser Parametrisierung erhalten wir also dasselbe Ergebnis,
wie dies aus geometrischen Gründen auch sein muß: Die Bogenlänge
ist schließlich eine Eigenschaft einer Kurve, nicht einer speziellen Parametrisierung der Kurve.
1
2
0.5
Die Bogenlänge ist somit
-1
-0.5
0
Wie Abbildung 70 zeigt, ist diese Annäherung der Kreislinie durch
Strecken erheblich unregelmäßiger als die obige, aber beim Übergang
zu immer feiner werdenden Unterteilungen gehen natürlich trotzdem alle
Streckenlängen gegen null. (Eingezeichnet sind die Strecken zu einer
Unterteilung des Intervalls [ 10 10] in Teilintervalle der Länge 1 2.)
-0.5
Abb. 70: Approximation durch Strecken in der rationalen Parametrisierung
-1
0.5
1
Kap. 2: Mehrdimensionale Analysis

2 ( 2 + 1)2
=
=
( 2 + 1)2
2
.
2+1
2( 2 1)
=
,
( 2 + 1)2
=
$
1)2
1
(4 )2 + 4( 2
( 2 + 1)2
2
©
) =
$
( 2 + 1) 2 2
=
( 2 + 1)2
©
1) 2
3(
(2
( 2 + 1) 2
( 2 + 1)2
2
2+1
=
<
d.h.
1
2+1
3:
und

2
.
h
Berechnen wir zunächst die Ableitung von
)
hier ist die Bogenlänge im Sinne obiger Definition nicht erklärt, jedoch
können wir natürlich 3 auf endliche Intervalle einschränken und diese
immer größer werden lassen; falls ein Grenzwert existiert, bekommen
wir also hier die Bogenlänge als uneigentliches Integral
<
;
2
2+1

3:
1
2+1
2

2
Alternativ hatten wir die Kreislinie auch parametrisiert durch
wie erwartet; zumindest für diese Parametrisierung ist also alles vernünftig.
Höhere Mathematik I SS 2007
%
$
"
" JKJK
JKJ e
"
%
Ï \
B
@
<
Ï <
1
B
@
1
B
@
©
©
Ï ©
©
©
B
@
B
Ê
È
È
@
©
©
È
()
.
( )
( )
e
Ê
Å©
Ï \
$
Å©
def
Ô
Ê
Ê
©
()
()
.
Å©
©
Ï ©
v
\
( )
Definition:
lang .
gegen
heißt RIEMANN-STIELTJES-Integral über
Analog definieren wir auch das Integral über eine Kurve .
( )
=
betrachten, und diese konvergieren wegen der Stetigkeit von
=0
1
h
g
h
Ô
©
h
Ò
<
ent-
( steht hier für das Bogenelement der Kurve, wobei der Buchstabe
wohl vom lateinischen spatium = Entfernung kommen dürfte.)
D
B
1
D 8
(
) sei ein stetiges Vektorfeld auf der offenen
, und : [ ]
sei ein Kurvenstück. Das Integral
1
È
©
0
<
Definition: a)
Teilmenge
©
we
nach Definition eines Kurvenstücks stetig differenzierbar ist, ist
()
( ) für ein stetiges Vektorfeld eine stetige und damit insbesondere RIEMANN-integrierbare Funktion; wir wissen also, daß der
Grenzwert für immer enger werdende Verfeinerungen der Unterteilung
existiert und gleich dem Integral über diese Funktion ist.

©
Wenn wir wieder von derselben Unterteilung wie oben ausgehen und das
Kurvenstück durch eine Folge von Tangentenvektoren approximieren,
müssen wir hier die Summen
©
h
JKJ
Å©
J J
K
©
Da
()
( )
ÏÑÐ
Noch allgemeiner können wir ausgehen von einer beliebigen stetigen
Funktion :
auf dem Bild
=
[ ] des Kurvenstücks
:[ ]
und diese entlang integrieren. Als Motivation könnte
()
man sich etwa vorstellen, daß eine materielle Kurve ist und
die (lineare) Massendichte im Punkt ( ) angibt, oder könnte den Weg
eines Teilchens durch eine Flüssigkeit mit räumlich variabler Viskosität
beschreiben usw.

JKJ
Ê
Å©
JKJ
Ê
©
( )
Ô
ÏÑÐ
©
=0
\
1
\
@
und wählen in jedem Teilintervall (
+1 ) einen Punkt . Zwischen den
Punkten ( ) und ( +1 ) approximieren wir die Kurve wie im vorigen
Abschnitt durch den Tangentenvektor ( ) ( +1
), die Arbeit kann
dann angenähert werden durch
e
Ï Ð
g
©
=
h
©
©
©
1
ÏÓÐ
e
ÏÑÐ
©
B
1
w
0
=
def
Å©
=
( )
Um die Gesamtarbeit zunächst näherungsweise auszurechen, unterteilen
wir wie gewohnt das Intervall [ ] durch Zwischenpunkte
ist
h
Gehen wir der Einfachheit halber aus von einem Kraftfeld ( ) und
einem Teilchen, das sich entlang eines Kurvenstücks : [ ]
durch dieses Feld bewegt, d.h. der Vektor
( ) sei für alle aus [ ]
definiert. Im Punkt ( ) greift dann also der Kraftvektor
( ) an; die
Arbeit, die das Teilchen verrichten muß oder gewinnt, ist das Skalarprodukt aus Kraftvektor und (Tangential-)Vektor des Wegs.
entlang
Kap. 2: Mehrdimensionale Analysis
%
b) Das Integral über entlang einer Kurve ist die Summe der Integrale
über entlang der Kurvenstücke, aus denen zusammengesetzt ist.
über
©
Die Hauptanwendung von Kurvenintegralen besteht nicht darin, die
Längen aller möglicher Kurven zu berechnen; der Hauptgrund, warum
wir solche Integrale betrachten, ist die Berechnung der aufzuwendenden
oder freiwerdenden Energie bei der Bewegung eines Teilchens in einem
Kraftfeld bzw. – im Fall eines elektrisch geladenen Teilchens – eines
elektromagnetischen Felds.
c) Integration eines Vektorfelds längs einer Kurve
Höhere Mathematik I SS 2007
%
@
ÏÑÐ
DE
©
<
%
Ô
e
|
Ô
e
h
h
Ô
ÕÔ
A
,
,
wobei + jene Kurve bezeichne, deren erste Kurvenstücke die Kurve
definieren, während die restlichen die Bestandteile von sind.
Schließlich haben wir auch noch einen
©
@
©
B
@
©
Mittelwertsatz: Für jedes Kurvenstück : [ ]
Funktion auf ([ ]) gibt es einen Parameterwert
gilt
1
Ê
e
©
Å©
Ï Ð
= ( ) Bogenlänge von
.
h
©
©
Ô
JzJ
Å©
J J
z
und jede stetige
[ ], so daß

Ï Ð
©
()
Å©
©

1
©
Å©
©
©
Es ist hier nicht wesentlich, daß als Kurvenstück vorausgesetzt war;
ein einfaches Argument mit dem Zwischenwertsatz zeigt, daß der Mittelwertsatz auch für Kurven gilt. Wesentlich ist dagegen die Stetigkeit
von , denn da der der Mittelwertsatz der Integralrechnung nur für stetige Funktionen gilt, können wir ihn nur anwenden, wenn
( ) stetig
ist. Ein einfaches Gegenbeispiel zum Mittelwertsatz wäre eine Kurve aus
zwei gleichlangen Komponenten, auf deren einer konstant gleich eins
ist, während es auf der anderen verschwindet. Nach dem Mittelwertsatz,
angewandt auf die beiden Komponenten, folgt, daß der Mittelwert über
die gesamte Kurve gleich 1/2 ist, aber dieser Wert wird von nirgends
angenommen.
( ).
Beweis: Dies ist einfach der gewöhnliche Mittelwertsatz der Integralrechnung, angewandt auf die Funktion
©
( ) für jeden Punkt auf ,
y
Õ
B
Ê
\
e
falls ( )
|
8
( )
e
h
<
\
( )
}
Natürlich gelten auch für RIEMANN-STIELTJES-Integrale die üblichen,
aus der klassischen Integralrechung bekannten Rechenregeln: Da wir
Kurvenintegrale als spezielle RIEMANN-Integrale definiert haben, sind
dies in der Tat einfach Spezialfälle der dortigen Regeln. Wir haben also,
zum Beispiel, wieder die Monotonieregel
h
Ô
+
+
=
h
und für Zusammensetzungen gilt
+
e
y
A
@
zum Integral entlang über das Vektorfeld . (Falls sich die Kurve
selbst schneidet, wie etwa eine 8, ist ( ) im Schnittpunkt eventuell nicht
nur vom Punkt ( ) abhängig, sondern vom Parameter , so daß wir dann
nicht in der Situation von RIEMANN-STIELTJES sind. Meist ist dies jedoch
kein Problem, denn wenn so etwas nur endlich oft vorkommt, können
wir die Kurve in endlich viele Kurvenstücke zerlegen, deren jedes die
Voraussetzung erfüllt.)
=
B
()
()
()
)
©
() =
e
}
+
e
(
h
1 zur BoDieses RIEMANN-STIELTJES-Integral wird im Spezialfall
genlänge, und für ein reguläres Kurvenstück ohne Selbstschnitte wird
es für
die Linearitätseigenschaft
Kap. 2: Mehrdimensionale Analysis
%
sein Lebensende blieb. Seine Arbeiten befassen sich vor allem mit Verbindungen zwischen
der Zahlentheorie und der Analysis; das RIEMANN-STIELTJES-Integral wurde in einer
Arbeit über Kettenbrüche eingeführt.
Der niederländische Mathematiker THOMAS JAN STIELTJES (1856–1894) studierte in Leiden, schwänzte dort
aber viele Vorlesungen um stattdessen die Werke von
GAUSS und JACOBI zu lesen. Obwohl er bei seinen
Prüfungen dreimal durchfiel, wurde er Assistent am
Observatorium von Leiden, dessen Direktor ein Freund
seines Vaters war. 1883 heiratete er und wechselte unter
anderem auf Betreiben seiner Frau von der Astronomie
zur Mathematik. Nachdem eine Berufung nach Groningen an seinem fehlenden Hochschulabschluß gescheitert war, übersiedelte er 1885 nach Frankreich, wo er
Professor an der Universität Toulouse wurde und bis an
Höhere Mathematik I SS 2007
©
©
©
\
m
y
h
\
e
y
h
Ô
m
Ô
Als nächstes kommen wir zu der angekündigten Unabhängigkeit des
Kurvenintegrals von der Parametrisierung der Kurve. Da diese, wie wir
am Beispiel der mehrfach durchlaufenenen Kreislinie gesehen haben,
nicht ganz uneingeschränkt gilt, müssen wir zunächst definieren, was
wir meinen:
%
Höhere Mathematik I SS 2007
©
<
h
A
B
<

1
h
1
und : [ ]
heiDefinition: Zwei Kurvenstücke : [ ]
ßen äquivalent, wenn es eine bijektive stetig differenzierbare Abbildung
:[ ]
[ ] gibt mit ( ) = und ( ) = derart, daß
=
ist, d.h. für alle
[ ] ist
( ) = ( ).
A®Ö
@
B

@
©
©
@

h
1

A
B
8
@
h
A
B

Dese Definition stellt insbesondere sicher, daß [ ] und [ ]
dieselbe Teilmenge von
sind, so daß die beiden Kurven als Punktmengen übereinstimmen; durch die geforderte Bijektivität von ist aber
auch sichergestellt, daß die Kurve bei beiden Parametrisierungen gleich
oft durchlaufen wird. Daher erwarten wir
<
©
DE
1
h
A
<
1
<
<
B
DE
1
e
h
e
D
\
Õ
h
\
Ô
h
B
@

Å©
Å
AÖ
©
Ï $

w
e
w
e
Å
JzJKJ

ÅA
JzJKJ
(

A
'
G
h
ÅAÖ
G
e

g
h
\
Ô
.
Ø×
Ù
Ï g
e
Å©
©
6
e
\
( )

=
grad
<
1
©
B
@
h
$
h
Õ
h
JKJKJ
ÅA
JKJKJ
A
~
Ï () =
¨( ) ,
eines Himmelskörpers oder, allgemeiner, durch irgendein Potentialfeld
= grad . Nach dem zweiten NEWTONschen Gesetz gilt dann für
3
des Teilchens mit der Zeit als Parameter
die Bahn : [ ]
=
c
()
Ï Ð
l
()
$
c
=

()

()
D
()
1
Zum Verständnis des Begriffs konservativ betrachten wir ein Beispiel
aus der Physik: Ein Teilchen mit konstanter Masse bewege sich durch
das Gravitationsfeld
<
=
ÏÑÐ
()
Ï Ð
()
Ô
b) Das Vektorfeld
heißt konservativ, wenn es eine differenzierbare
Funktion :
gibt, so daß = grad ist. heißt Stammfunktion
von und
Potentialfunktion.

=
= 0.
heißt zirkulationsfrei, wenn

( )
©
e
h
ÏÑÐ
Der Beweis ist eine einfache Anwendung der Kettenregel und der Substitutionsregel: Nach Definition der Äquivalenz gibt es eine bijektive
stetig differenzierbare Funktion mit ( ) = und ( ) = , so daß
=
und damit = (
)
ist. Offensichtlich muß monoton
wachsen, also ist ( ) nirgends negativ und somit gleich seinem Betrag.
Nach der Substitutionsregel ist
©
@
gilt:
D
.
D
( )
ÏÑÐ
Definition: a) Ein Vektorfeld :
für jede geschlossene Kurve in
1
=
und : [ ]
seien äquisei eine stetige Funktion. Dann
<
( )
@
Lemma: : [ ]
valente Kurvenstücke, und :
ist
%
Wir haben Kurvenintegrale über Vektorfelder eingeführt, um die Energie
zu beschreiben, die zur Bewegung eines Teilchens durch ein Kraftfeld (oder ein elektromagnetisches Feld) aufgewendet werden muß
oder dabei frei wird. Das gerade bewiesene Lemma zeigt, daß diese
(Gesamt-)Energie nur vom Weg des Teilchens abhängt, nicht aber beispielsweise von seiner Geschwindigkeit. Wie aus der Physik bekannt
ist, hängt aber beispielsweise bei reibungsfreier Bewegung eines Teilchens in einem mechanischen Kraftfeld der Weg nicht einmal von der
Kurve ab, sondern nur von deren Anfangs- und Endpunkt oder, genauer
gesagt, vom der potentiellen Energie des Anfangs- und des Endpunkts.
Insbesondere verschwindet also das Integral längs einer jeden geschlossenen Kurve. In diesem Abschnitt wollen wir Vektorfelder mit dieser
Eigenschaft genauer untersuchen.
d) Zirkulationsfreie und konservative Vektorfelder
Kap. 2: Mehrdimensionale Analysis
c
©
©
%
©
©
©
Ù
c
©
Û
Û
á
Û
à
ß
Å©
Å©
ß
á
Û
c
©
h
'
ß
Å©
(
©
Ù
c
©
Ù
Å©
Å©
h
Û
Û
Û
Ûâ
Û
ã
Ûâ
Û
Ûâ
ß
ß
Û
Û
Û
Damit ist also Vereinigung der offenen und disjunkten Teilmengen 0 und
0;
wenn
zusammenhängend ist, geht das nur, wenn eine der beiden Mengen leer ist.
= 0 . Also kann jeder Punkt
0 enthält den Punkt 0 , also ist
0 = und somit
aus
durch einen Weg mit 0 verbunden werden, und damit ist
zusammenhängend
im Sinne der obigen Definition.
Û
Ú
©
Ù
JKJ
Å©
JKc J
D
<

DE
Ï Ð
1.)
ist konservativ.
2.) Es gibt eine Funktion :
1
D
=
<
, so daß für jede Kurve
e
@
( ) ;
©

B $
©
1

h
Ï Ð
Ô
Ï Ð
<
gilt:
insbesondere hängt das Integral also nur von den Endpunkten von
ab.
3.)
ist zirkulationsfrei.
( )
in
auf einer offenen zusammenhänsind die folgenden Aussagen äquivalent:
Ï Ð
:
<
Satz: Für ein Vektorfeld
genden Teilmenge
Der folgdende Satz zeigt die Äquivalenz der Begriffe konservativ und
zirkulationsfrei; wegen seiner zweiten Aussage kann er als das mehrdimensionale Analogon des Hauptsatzes der Differential- und Integralrechung aufgefaßt werden.
Û
©
\
©
DE
8
_
\ _
Û
D
Û
Diese Definition fordert zwar genau das, was wir gleich brauchen werden, sie ist aber nicht
die übliche Definition einer zusammenhängenden Menge: In der Analysis wie auch in der
Topologie bezeichnet man eine Menge dann als zusammenhängend, wenn sie nicht als
disjunkte Vereinigung zweier offener Teilmengen von geschrieben werden kann; dies
Û
Û
heißt zusammenhängend, wenn es
eine Kurve gibt mit Anfangspunkt
á
ß
D
Definition: Eine Teilmenge
zu je zwei Punkten
und Endpunkt .
Û
Ûâ
Wie zu erwarten, sind die beiden Begriffe konservativ und zirkulationsfrei nicht unabhängig voneinander; tatsächlich werden wir gleich
sehen, daß sie sogar äquivalent sind. Aus technischen Gründen wollen
uns uns dabei, auch wenn es nicht unbedingt nötig wäre, auf sogenannte
zusammenhängende Mengen beschränken:
Û
ß
Der Name konservativ“ kommt vom lateinischen conservare = erhal”
ten; der Grund für das negative Vorzeichen der Potentialfunktion liegt
darin, daß der Gradient in Richtung des stärksten Anstiegs einer Funktion
zeigt, wohingegen die Natur versucht, ein System zum Energieminimum
zu bringen, so daß die Kräfte in Gegenrichtung zum Gradienten wirken.
ß
ß
2
ß
Aber auch das Komplement von 0 in ist offen, denn auch für einen Punkt 2
0
enthält eine -Umgebung. Läge diese nicht ganz in
0 , gäbe es dort einen Punkt 3 ,
der durch einen geeigneten Weg mit 0 verbunden werden könnte. Da aber 3 durch eine
Strecke mit 2 verbunden werden kann, gäbe dann auch einen Weg von 2 nach 0 , im
Widerspruch zur Annahme. Also ist
0 offen.
Ûâ
à
Û
()
()
+
2
konstant, und das ist der klassische Energieerhaltungssatz: Die Summe
aus kinetischer und potentieller Energie ist eine zeitlich unveränderliche
Erhaltungsgröße.
ß
ß
=
Û
()
()
Û
( ) ( )+
2
nach Produkt- und Kettenregel. Also ist
()
à
=
( ) + grad
¨( )
Û
0=
Û
Sei nämlich 0 die Menge aller Punkte aus der offenen Menge , die mit dem Punkt
durch einen Weg verbunden werden können. Dann ist 0 offen, denn für 1
0
0
eine -Umgebung von 1 , die ganz in
liegt. Da
gibt es wegen der Offenheit von
jeder Punkt dieser -Umgebung durch eine Strecke mit dem Mittelpunkt 1 verbunden
werden kann, liegt auch diese Umgebung in 0 , d.h. 0 ist offen.
Û
ß
Um aus dieser Vektorgleichung eine skalare Beziehung abzuleiten, bilden wir das Skalarprodukt mit dem Geschwindigkeitsvektor ( ):
ÛÜ
Û
( ) = 0.
ÝÞ
ist im allgemeinen eine schwächere Bedingung als die hier geforderte. Für eine offene
sind die beiden Definitionen aber äquivalent:
Teilmenge
Kap. 2: Mehrdimensionale Analysis
%
¨ ( ) + grad
d.h. die im Punkt ( ) wirkende Kraft ist gleich der Masse des Teilchens
mal seiner Beschleunigung. Also ist in jedem Punkt ( )
Höhere Mathematik I SS 2007
©
D
1
B
@
©
Ï Ð
Beweis: 1 )
2 ): Falls konservativ ist, gibt es eine Stammfunktion
auf , so daß = grad ist. Für eine Kurve : [ ]
ist daher

-
5

Ï Ð
5
D
%
()
w
e
e
e
grad
Å©
Å©
ÑÏ Ð
h
Ï Ð
g
Ô
w
h
©

g
h
©
h
e
©

B $
©

h
©
h
g
-
5
5
-
5
5
A
h
Ï Ð
)
ê

A
h
©
( )
ä
0
0
1
=
= lim
Ð ê
A
s ©
A
<
h
1
A
A
<
h
$

1
1
A ä

Ï ) $

ä
A
0
=
ab und
.
( +
)
)
,
=
( )
in Richtung des Einheits-
( +
e

!
\

!
ä
A
©
A
s ©
5
5
5 r
©
A
ä
ä
A
A
5
5
©
5 r
©§¦
5
5
5
e
e
e
e
Im 3 sollten wir erwarten, daß es noch eine vierte äquivalente Charakterisierung konservativer Vektorfelder gibt: Da die Zirkulationsfreiheit
mit Drehungen um eine Achse zusammenhängt, sollte für solche Felder
auch die Rotation verschwinden. Diese Richtung ist trivial:
nach dem Hauptsatz der Differential- und Integralrechnung für Funktionen einer reellen Veränderlichen. Dies zeigt, daß grad = ist und das
Vektorfeld somit eine Stammfunktion hat.
( +
e
0
e
lim
h

h
Ï Ð
h $
ÏÑÐ
h
ÏÑÐ
h
Ï Ð
h
Ï Ð
Ô
A
e
Õå
s
©
Ô
Ô
und gleich.
Ï )
und damit
=
Ð \
Ð und damit sind die Integrale über

,
$
h
=
\
Ï )
Ï )
+

h
ÏÓÐ
=
ÏÑ
Ï
\
Ð 0=
\
Ï )

e
das rückwärts durchlaufene Kurvenstück zu ; ist die Anzahl der , so
bestehe die Kurve aus den Kurvenstücken
1 . Da und dieselben Anfangs- und Endpunkte haben, ist der Endpunkt von gleich
dem Anfangspunkt von und umgekehrt; die Folge von Kurvenstücken
1
1 ist deshalb eine geschlossene Kurve . Nach Voraussetzung verschwindet das Integral längs einer solchen Kurve, d.h.
é¿
ÔIç
Speziell für einen Vektor =
der Länge
vektors der Koordinatenachse ist
h $
Ï Ð

)
e

( +
+
Ôç
;
;
e
]
\
( )=
ÏÑ
( + )
D
:[
\
h
ÏÑÐ
von
©aæ
Für einen hinreichend kleinen Vektor liegt auch die Verbindungsstrecke von mit + in und kann durch eine Kurve parametrisiert
werden; dann ist

ê
]

( ) in der Tat nur von
Ôç
e
:[
\
wegen der Voraussetzung 2) hängt
nicht von der Wahl des Wegs .
( )=
e
\
Ï
h
ÏÑÐ
Konkret sei für ein Kurvenstück
-
è
2 ): Zumindest anschaulich ist auch hier klar, was wir machen:
3)
Wir durchlaufen zunächst die Kurve in der üblichen Weise und dann
die Kurve rückwärts“. Dies ergibt eine geschlossene Kurve , auf die
”
wir 3.) anwenden können.
\
\
2)
3 ): Diese Implikation ist klar, denn wenn der Wert des Integrals
nicht von der Kurve abhängt, ist das Integral längs einer geschlossenen Kurve gleich dem Integral längs der zu einem Punkt degenerierten
Kurve, und das ist natürlich gleich Null.
\
h
ÏÑÐ
Damit ist das Integral, genau wie wir es vom Eindimensionalen gewohnt
sind, einfach gleich der Differenz der Werte der Stammfunktion am
Endpunkt und am Anfangspunkt der Kurve.
\
Wir definieren nun einen Kandidaten für eine Stammfunktion durch
\
( ) .
()
8
( )
()
D
=
=
D
()
()
D
=
w
=
©aæ
2)
1): 0 sei irgendein beliebig ausgewählter Punkt von . Da zueine Kurve
sammenhängend ist, gibt es dann für jeden Punkt
mit Anfangspunkt 0 und Endpunkt .
Kap. 2: Mehrdimensionale Analysis
%
nach der Kettenregel
Höhere Mathematik I SS 2007
<
A
Õ
D

Ï Ð
%
ÏÓÐ
:
3
auf
3
<
DE
<
D
1
°
ÏÑÐ
2
:
0
$
:
q
: °
.
Wie wir in 2e2) gesehen haben, verschwindet seine Rotation im gesamten Definitionsbereich des Vektorfelds, d.h. überall außerhalb der
-Achse.
(

1
)= 2
+
Die umgekehrte Richtung allerdings ist zumindest in dieser Allgemeinheit falsch. Als Gegenbeispiel betrachten wir das Magnetfeld eines
geradlinigen stromdurchflossenen Leiters, d.h. also (abgesehen von konstanten Vorfaktoren) das Vektorfeld
q
©

<
= e
e
Å©
Ï Ð
h
Ï Ð
©
=2 .
sin
cos
0
sin
cos
0
:
:
:
= e
Ô
Formal gehen wir dazu wie folgt vor: Wir wählen ein festes Koordinatenund betrachten Quader
, deren Kanten parallel zu
system im
denn Koordinatenachsen sind. (Für = 2 sind diese Quader“ natürlich
”
Rechtecke, und für = 1 Intervalle.) Das Volumen eines solchen Quaders soll gleich dem Produkt seiner Kantenlängen sein, genau wie wir
es aus der Elementargeometrie gewohnt sind.
h

q
$

= $e
h
<
h
q
ÏÓÐ
Der Grund für dieses Verhalten liegt, wie wir bald sehen werden, darin, daß
auf der -Achse nicht definiert ist: Obwohl die -Achse
im Vergleich zum gesamten 3 nur einen – sollte man meinen – vernachlässigbar geringen Teil ausmacht, genügt selbst diese minimale
Definitionslücke, um die Umkehrung des Lemmas falsch zu machen.
:
Ganz entsprechend müssen für dreidimensionale Bereiche Quader betrachtet werden, deren drei Seiten mit Verfeinerung der Überdeckung
immer kleiner werden, usw.
0
0

2
1
()
()
=
0
=
1
2
<
2
Bei der Definition des RIEMANN-Integrals wird die Fläche unterhalb der
Kurve durch Rechtecke angenähert, deren Kantenlänge in -Richtung
immer kleiner wird, während die Kantenlänge in -Richtung durch die
-Koordinaten der Kurve = ( ) gegeben war. Im allgemeinen Fall, wo
es keine ausgezeichnete Richtung mehr gibt, wird diese Unterscheidung
zwischen - und -Richtung offensichtlich sinnlos; die einzig mögliche
Verallgemeinerung des RIEMANN-Integrals besteht darin, daß man eine
Fläche durch beliebige Rechtecke annähert und beim Grenzübergang
beide Seiten gegen Null gehen läßt.
<
ist
Beginnen wir mit Flächeninhalten und Volumina. Bereits das gewöhnliche RIEMANN-Integral kann als Flächeninhalt interpretiert werden, allerdings nur für die Fläche zwischen der -Achse und einer Kurve zwischen
zwei gegebenen -Koordinaten. Hier soll es nun um beliebige Flächen
im 2 , Volumina im 3 und die entsprechenden höherdimensionalen
Konzepte gehen.
a) Flächeninhalte und Volumina
Trotzdem ist das Vektorfeld nicht zirkulationsfrei, denn für den Einheitskreis
3
;
: [0 2 ]
(cos sin 0)
%
Die bisher betrachteten Kurvenintegrale waren alle zurückführbar auf
gewöhnliche RIEMANN-Integrale über Funktionen einer reellen Veränderlichen. Mit ihrer Hilfe ist es möglich, die Länge von Kurven zu
bestimmen, nicht aber Flächeninhalte oder Volumen von höherdimensionalen geometrischen Gebilden. Deren Berechnung, sowie die von naheliegenden Verallgemeinerungen wie dem Fluß durch die Oberfläche
eines Bereichs sind Gegenstand dieses Paragraphen.
§5: Mehrdimensionale Integrationstheorie
Kap. 2: Mehrdimensionale Analysis
%
Beweis: Nach dem gerade bewiesenen Satz ist ein zirkulationsfreies Vektorfeld konservativ, und nach den Rechenregeln aus 2f) verschwindet
die Rotation eines Gradienten.
Lemma: Für ein zirkulationsfreies Vektorfeld
ist rot
0 auf .
Höhere Mathematik I SS 2007
<
ª
ë
<
Höhere Mathematik I SS 2007
%
<
<
ë
Ú
<
Ú
Ú

:
ì
ì
<
ë
10 Quadraten
Die Definition des Volumens ist nun fast selbstverständlich:
Abb. 71: Approximation einer Kreisfläche auf 10
Die Abbildungen 71 und 72 zeigen die Annäherung einer Kreisfläche
durch Elementarmengen von innen und außen; Abbildung 73 zeigt entsprechende Elementarmengen für eine Halbkugel.
ì
·
ì

ì
ë
ì

ì
JKJ
Ú
ÚE

ì
Ganz entsprechend können wir auch Integrale über Funktionen definiesei eine Funktion auf der Teilmenge
, und
ren: :
Definition: Wir sagen, die Menge
habe das Volumen ( ), falls
das untere Volumen ( ) und das obere Volumen ( ) beide existieren
und gleich ( ) sind.
<
falls dieses Supremum existiert. (Es existiert offensichtlich genau dann,
wenn die Menge beschränkt ist; für unbeschränkte Mengen wie etwa
den gesamten
ist die Menge aller ( ) unbeschränkt, so daß kein
Supremum existiert.)
ì

¸
Elementarmenge ,

ì
( )

def
·
î
( ) = sup
Úí
Entsprechend betrachten wir zur Definition des Volumens einer Teilmenge
Elementarmengen, die ganz in enthalten sind und
bezeichnen den Grenzwert bei immer feiner werdenden Quader als unteres Volumen ( ). Zur exakten Definition verwenden wir besser nicht
einen Grenzwert, da es etwas umständlich wäre, hier zu definieren,
über was genau wir den Grenzwert bilden, sondern wir definieren ( )
einfach als Supremum der Volumina aller Elementarmengen, die in
liegen:
ì
ì
falls dieses Infimum existiert. (Auch hier ist die Existenz wieder an die
Beschränktheit von gekoppelt, denn für ein unbeschränkte Menge
gibt es keine Elementarmenge, die enthält, so daß wir das Infimum
über die leere Menge bilden müßten.)
ì
Nun gehen wir im wesentlichen genauso vor, wie bei der Definition des
RIEMANN-Integrals: Dort hatten wir die Fläche unterhalb einer Kurve
= ( ) sowohl von oben als auch von unten durch Rechtecke angenähert; die Flächen der entsprechenden Elementarmengen hatten wir
als RIEMANNsche Unter- bzw. Obersummen bezeichnet. Das Integral
existierte nach Definition genau dann, wenn bei immer weiterer Verfeinerung der Überdeckung die Untersummen und die Obersummen gegen
einen gemeinsamen Grenzwert konvergierten.
ì
Das Volumen ( ) einer Elementarmenge
definieren wir als die
Summe der Volumina der endlich vielen Quader, aus denen die Menge
besteht; man überlegt sich leicht, daß es unabhängig von der Art der
Zerlegung der Menge in Quader ist.

Elementarmenge ,
ì
Im 2 wäre also beispielsweise jede Menge, deren Rand auf kariertem Papier so gezeichnet werden kann, daß alle Linien auf Karokanten
liegen, eine Elementarmenge.
JzJ
Ú
( )
¸
( ) = inf
ì
def
Genauso definieren wir ein oberes Volumen ( ) als Infimum der Volumina aller Elementarmengen, die enthalten:
%
Definition: Eine Elementarmenge in
ist eine Teilmenge
,
die als Vereinigung endlich vieler Quader mit achsenparallelen Kanten
geschrieben werden kann; dabei dürfen sich zwei Quader höchstens in
gemeinsamen Randpunkten schneiden.
Kap. 2: Mehrdimensionale Analysis
Ú

<
<
DE
<
D
1
\
v
òñ
,
( )
\
v
ñ
î
3
e
e
(
ñ
e
e
e
)
)
: ì
ë
ñ
2
also
.
soll dabei bedeuten, daß wir
D
ìE
e
ì
1
ì

ª
D
ÚE
È
¸
D
ª
ì
e
ª
\
( )
h
e
1
=
schreiben, andererseits ist, völlig analog zur Flächeninterpretation des
RIEMANN-Integrals, für eine auf nichtnegative Funktion
e
( )=
1
Integrale und Volumina sind natürlich eng miteinander verwandt: Einerseits läßt sich das Volumen eines Bereichs auch als
(Nicht alle Lehrbücher verwenden bei der mehrdimensionalen Integration mehrere Integralzeichen; einige, wie etwa [D], schreiben unabhängig
von der Dimension immer nur ein Integralzeichen. In Physik und Technik scheint die Schreibweise mit mehreren Integralzeichen üblicher zu
sein; deshalb soll auch hier diese Konvention verwendet werden.)
<
(
1
und für
Integralzeichen schreiben, für
Die Schreibweise
Menge aller RIEMANNscher Untersummen gleich dem Infimum der Menge aller RIEMANNscher Obersummen ist; dieser gemeinsame Wert ist der
Wert des Integrals.
v
v
ì
q
h
h
ª È
ì
5
5
5
8
JzJ
\
»
\

beste-
b
5
:
Die RIEMANNsche Obersumme für die Elementarmenge
h
5
5
h
.
5
5
ë
ì
( )

5
h
) inf
h
h
:
(
ª b
<
h
h
=1
5
:
q
MANNsche
5
h
h
h
Abb. 73: Approximation einer Halbkugel durch Würfel
50 Quadraten
JKJ
\
»
existiert, wenn das Supremum der
\
1
( )
8
( )
5
) sup
ist entsprechend
ª b
Definition:
(
=1
1
ð
ª ï
und wir definieren
ï
¸
sei eine Teilmenge von . Dann können wir wieder RIEUntersummen definieren, indem wir eine Elementarmenge
betrachten, bestehend etwa aus den Quadern 1
, und
dazu die RIEMANNsche Untersumme definieren als
%
ª
hend aus den Quadern
Kap. 2: Mehrdimensionale Analysis
%
Abb. 72: Approximation einer Kreisfläche auf 50
Höhere Mathematik I SS 2007
ì
Úí
7
)
+1
JKJzJKJ
(
0
1
)
(
8
5
5
5

m
:
1
und
)
.
1
ó
ì
5
5
5
m
:
<
8
5
5
5
e
e
h
h
h
e
h
\
y
e
ì
m
ì
\
ì
m
\
y
8
\
e
e
}
h
h
h
\
y
\
ì
\
e
h
e
h
|
h
e
\
y
e
ì
}
\
|
ì
ì
ë
ì
8
\
e
e
B

B
\
8
ì
h
<
h
@
Ê
@

<
ì
1

\
\
ì
<
so daß
()
\
·
<
ì
ë
ì
8
\
ì
2
und 0
1
ì
8
:
JKJ
<
8
:
9
m
\
aller Punkte mit rationalen Koordianten im Einheitsquadrat betrachten.
Da keine reellen Intervalle enthält, sind alle Rechtecke, die ganz in
enthalten sind, zu Punkten degeneriert. Eine in enthaltene Elementarmenge besteht also aus endlich vielen Punkten und hat somit den
= (
)
Wie beim gewöhnlichen (eindimensionalen) RIEMANN-Integral ist die
Existenz von mehrdimensionalen Integralen normalerweise kein Problem, allerdings kann man natürlich leicht Beispiele konstruieren, für
die das Integral nicht existiert. Wir können etwa in Analogie zur DIRICHLETschen Sprungfunktion die Menge

( )
@
9
1)
\
m
e
e
= (
1
è
m
\
h
h
1
\
\
mit ( ) = ( 1 ) und ( ) = ( 2 ). Nach dem Zwischenwertsatz gibt
es dazu ein
[
] mit ( ) = ; mit 0 = ( ) ist also ( 0 ) = .
Damit ist der Satz vollständig bewiesen.

:
1)
;
\
m
(
]
B
1
¸
nach der Monotonieregel ist daher
\
<
:[
2) ;
è
©
©
(
( )
Ê
( )
@
\
1)
B
(
ì
è
ì
8
Der Beweis geht ganz genauso wie in : Eine stetige Funktion nimmt
auf einem abgeschlossenen Intervall sowohl ihr Maximum als auch ihr
Minimum an; genauso zeigt man, daß eine stetige Funktion auf einer
ihr Maximum und ihr
beschränkten abgeschlossen Teilmenge
Minimum annimmt. Sei etwa 1
ein Punkt, in dem minimal wird,
und 2 einer, in dem maximal wird. Dann ist für jedes
e
©
( ).
©
ist. Wir müssen noch zeigen, daß dieses ein Funktionswert von auf
ist. Dazu verbinden wir 1 und 2 durch eine Kurve ; indem wir nötigenfalls die Parameterintervalle der Kurvenstücke von verschieben,
können wir annehmen, daß durch ein zusammenhängendes Parameterintervall [
] parametrisiert wird. Wegen der Stetigkeit von haben
wir dann eine stetige Funktion
0)
=
2 ),
©
= (
1
1
und (
1)
ì
( )
Mittelwertsatz: Für einen zusammenhängenden abgeschlossenen und
und eine stetige Funktion :
gibt
beschränkten Bereich
es einen Punkt 0
, so daß gilt
e
Außerdem haben wir wieder einen
.
è
\
( )
h
1
ì
è
( )
\
h
+

1
ì
( )
zwischen (
( )
=
e
\
1
( )
h
\
( )+
ist. Damit gibt es eine Zahl
e
2)
\
= (
, und die Linearitätseigenschaft
h
1

( ) für alle
2)
(
,
ì
falls ( )
ì
,
1
( )
e
1
1
e
( )
\
( )
h
was wiederum kleiner oder gleich
kleiner oder gleich
Kap. 2: Mehrdimensionale Analysis
h
Auch für das so definierte mehrdimensionale Integral gelten aus offensichtlichen Gründen die Analoga der aus aus der eindimensionalen
Integralrechnung bekannten Rechenregeln wie die Monotonieregel
%
(
Höhere Mathematik I SS 2007
%
ì
\
ì

\
\
ì
ì
ì
%
Flächeninhalt null. Eine Elementarmenge, die ganz enthält, muß aber
das gesamte Einheitsquadrat enthalten, da die rationalen Punkte dort
dicht liegen; sie hat also mindestens die Fläche eins. Somit ist eins der
obere und null der untere Flächeninhalt von ; der Flächeninhalt von
existiert also nicht.
Höhere Mathematik I SS 2007
ì
1
der Grenzwert
<
Wie auch im Eindimensionalen genügt es hier nicht, nur eine einzige
zu betrachten; ansonsten könnte man beispielsFolge von Mengen
weise dem uneigentlichen Integral
existiert, und wenn er für jede solche Folge denselben Wert hat. Diesen
gemeinsamen Wert bezeichnen wir als den Wert des uneigentlichen
Integrals.
!"
ì
ì
ë
ì
ì
ì
e
sin sin
õ
ì
je nachdem, ob man für die
Quadrate nimmt, in deren Eckpunkten der Cosinus für beide Koordinaten verschwindet, oder Quadrate, in
deren Eckpunkten die beiden Cosinus einen konstanten anderen Wert
haben, dem Integral die verschiedensten Werte zuordnen. Tatsächlich
aber existiert dieses uneigentliche Integral natürlich genauso wenig wie
sin
.
das eindimensionale Integral
2
e
ì
ì
ì
ì
ì
"v
"
h
w
"
e
e
h
e
2
e
w
2
+
2
)
*
)
g
!"
g
õ
<
ìE
<
D
1
Der Grund dafür, daß wir bislang noch keine interessanten Beispiele für
mehrdimensionale Integrale haben, liegt natürlich darin, daß man Werte
von Integralen fast nie durch Anwendung der Definition bestimmt. Im
Eindimensionalen wird stattdessen meist den Hauptsatz der Differentialund Integralrechnung benutzt, über den die Berechnung eines Integrals
auf die (nicht immer explizit mögliche) Bestimmung einer Stammfunktion zurückgeführt wurde; hier, im Mehrdimensionalen, wollen wir die
b) Integration über Normalbereiche
berechnen werden.
(
Für interessantere Beispiele sei auf den nächsten Abschnitt verwiesen,
wo wir
h
ì
e
e
h
h
\
ì
ë
ì
ì
2
:
ë
ì
1
ì
h
h
existiere, wenn für jede Folge
:
1
( )
h
DE
Definition:
sei eine unbeschränkte Menge und die Funktion :
sei in einer umfassenden Menge
erklärt. Wir
sagen, das uneigentliche Integral
\
:
falls dieser Grenzwert existiert. Genauso definieren wir jetzt
e
e
h
,
h
( )
= lim

( )
=
ì
( )
ì
Für eine unbeschränkte Menge können wir bislang weder Volumen
noch Integrale definieren, denn unsere Konstruktion ist nur anwendbar,
wenn in einer Elementarmenge enthalten ist. Das ist allerdings nichts
neues, denn beim eindimensionalen RIEMANN-Integral tritt genau das
gleiche Problem auf und wird dadurch gelöst, daß man uneigentliche
Integrale einführt: Beispielsweise ist
1
ô
h
Die folgende Überlegung liefert ein Kriterium für die Existenz des Volumens einer Teilmenge
: Die Differenzmenge zwischen einer
Elementarmenge, die enthält, und einer Elementarmenge, die in
enthalten ist, kann offenbar wieder als Elementarmenge aufgefaßt werden und enthält den Rand von . Je besser die äußere und die innere
annähern, desto weniger unterscheidet sich diese
Elementarmenge
Differenzmenge vom Rand; die Existenz eines Volumens von ist daher äquivalent dazu, daß das Volumen des Rands von existiert und
verschwindet.
mit
ì
lim
von beschränkten Mengen
Kap. 2: Mehrdimensionale Analysis
%
<
ë
ë
%
B
·
ì
m
w
@
JKJ
<
e
8
e
.
( )
m
:
h
m
h
h
g
:
ñ
y
B
·
ì
m
m
@
JKJ
<
8
:

8
D
m
8
10
12
Abb. 74: Normalbereiche vom Typ I und II
6
w
e
e
e
D
ìE
=
1
e
h
h
h

:
*
Ì
e
g
h
h
:
e
:
ìE
:
ñ
ñ
y
$
g
:
=
Ë
D

Ë
6 e
e
)
.
.
14
g
:
Í
h
h
h
ì
Î
ì
w È
:
<
e
ö
Ì

e
ë
B

ì
~
:
:
ñ
B
8
@
<
m
@

m
y
<
1
B
@
y y
B
·
¸
( )
m
m
ì
:
m
m
@
JKJ
<
8
:
ì
h

B
8
:
@
2
:
y

1
h
·
ì
( ) .
¸
:
y
und ( )
m
)

= (
und
( )
h
<
ist. heißt Normalbereich vom Typ II, wenn es reelle Zahlen
stetig differenzierbare Funktionen
:[ ]
gibt mit ( )
für alle
[ ], so daß
und ( )

= (
2
:
)
Da die Aussage b) durch Vertauschung der beiden Koordinaten in a)
übergeht, reicht es, den Satz für Normalbereiche vom Typ I zu beweisen.
Für diese Normalbereiche können wir nicht nur die Fläche leicht ausrechnen, sondern auch beliebige Integrale über stetige Funktionen:
%
Beweis: Wir wissen bereits, daß der Flächeninhalt von existiert; da
eine stetige Funktion ist, folgt dann auch ohne größere Schwierigkeiten
die Existenz des Integrals von über . Wir wollen darauf nicht genauer eingehen, sondern nur benutzen, daß es dann ausreicht, spezielle
Folgen von Elementarmengen zu betrachten. Eine solche spezielle Folge
erhalten wir etwa dadurch, daß wir den ganzen 2 mit einem Quadraund ihr
tegitter überziehen; die Seitenlänge der Quadrate sei =
Flächeninhalt dementsprechend gleich 2 .
(
h
( )
( )
Î
)
ö
( )
:
vom Typ II ist
)
(
w
(
h
b) Für einen Normalbereich
)
* e
(

( )
.
Í
2
Definition: Eine Teilmenge
heißt Normalbereich vom Typ I,
wenn es reelle Zahlen
und stetig differenzierbare Funktionen
:[ ]
gibt mit ( )
( ) für alle
[ ], so daß
4
<
( )
2
Kap. 2: Mehrdimensionale Analysis
h
ausdrücken. Ähnliche Formeln gelten auch nach Vertauschung der Rollen von und .
y
@
DE
Satz: :
sei eine stetige Funktion auf
a) Für einen Normalbereich
vom Typ I ist
0
1
2
3
4
5
<
( )
B
=
m
:
], durch das eindimen-
m
[
( )
( ) ist für alle
und ( )
¸
läßt sich, wenn ( )
sionale Integral
2

= (
)
Auch den Flächeninhalt der etwas komplizierteren Menge
:
e
( )
m
=
und 0
¸
die Fläche
2
@
= (
B
)
Integration soweit wie möglich auf mehrfache eindimensionale Integration zurückführen. Zumindest in einem Fall wissen wir schon, wie das
geht: Ist die Funktion auf dem Intervall [ ] nichtnegativ, so hat
Höhere Mathematik I SS 2007
%
k
k
m
:
m
m
y m
m
:
JKJ
<
8
:
Ú È
÷
Ú È
i
Ú È

ì
ì
%
Ú È
r
Ë
ì
È
È
r
(
k
ì
« k
:
« Î

ù«
X
* ø
Ì
b
:
ù«
X

* ø
ª b

b
ì
ª
ª
b
i
m
m
i
m
k
Í
Ë
È
È
ª b
« k
:
« Î
ù
X
«
* ø
Ì
b
¦«
:

ù«
X
* ø
ª b

b
¦
«
12
÷
r
k
:
1
k
« k
:
« b

ù«
X

* ø
b
* e
2
,
=
¦«
h
2
2
h
e
,

ù«
X
* ø
:
:
ö
*
=0+
= sin cos
JKJKJKJ ,
2
2 1

=
w
=
1
1
2 1
sin2 cos
=
cos )
2
2
2
=
sin
2
2
,
h
e
* e
Ë
e
,
h
Í
h
:
Ì
2
e
2
2
=
(1
2
,
2
cos
2
$
=
ö
( )
=
,
,
$
,
e
)
h
(
,
( )
=
=
die RIEMANNschen Unter- und Obersummen daher entsprechend gegen
2
,
( )
2 1
e
=
;
2
2
$
1
2
2
.
,
2
cos
.
und das rechtsstehende Integral läßt sich mit partieller Integration ausrechnen:
1
1

)
1
1
(
ñ
( )
e
h
beide gegen
,
)
(
h
h
=
:
Zur Berechnung dieses Integrals können wir die Substitutionsregel anwenden: Mit = sin ist
1
e
e
=1
h
)
=
1
úKúKÌ
=
(
·
e
? ,
)
e

(
:
*
sup
ûKûKÎ
:
h
und
JKJ
$
<
)
:
Ë
(
8
? $
inf
8
als stetige Funktion RIEMANN-integrierbar ist, konvergieren für
und damit
0
m
:
Da
m
.
m
*
)
$
(
Í
)
m
h
sup
$
(
$
=

e
=1
:
)=
2
(
1
m

)
JKJ
$
<
2
1 und
$
:
2
2 .
= (
)
1
1 und
1
1
In der ersten Darstellung ist nach Teil a) des gerade bewiesenen Satzes
1
sup
2
m
(
ì
:
)
)
m
h
(
·
= (

$
=
1 ,
m

=1
ì
$
1
:

¸
1
ñ
auftreten; dann ist die
¸
Im -ten Streifen mögen die
mit
RIEMANNsche Obersumme gleich
:
kann sowohl als Normalbereich vom Typ wie auch als solcher vom
Typ II geschrieben werden:
ausrechnen wollen.
2
^
Für die RIEMANNsche Obersumme müssen wir alle Quadrate betrachten,
die mit nichtleeren Durchschnitt haben; dabei treten im allgemeinen
auch Quadrate
unterhalb von 1 auf, für deren Bezeichnung wir
Indizes
0 verwenden.
)
k
.
+
:
=1
)
Ú È
(
Í
=1
ì
)
b
inf
2
m
(
ª
1
$
=1
@
e
)=
ì
h
(
8
e
=1
B
h
)
die wir hier umständlich als
2
J J
K
<
(
·
= (
¸
1
ì
)
Als erstes Beispiel berechnen wir zur Kontrolle etwas Altbekanntes, die
Fläche der Einheitskreisscheibe
wie behauptet.
Kap. 2: Mehrdimensionale Analysis
%
inf
Als in enthaltene Elementarmenge
wählen wir die Menge aller
Quadrate, die ganz in liegen; als enthaltende Elementarmenge
entsprechend die Menge aller Quadrate, die nichtleeren Durchschnitt
mit
haben. Wir numerieren die Quadrate in
und
mit zwei
Indizes: Das Intervall [ ] wird durch das Quadrategitter in
1
Teilintervalle der Länge zerlegt; das Quadrat
liege über dem -ten
dieser Teilintervalle und sei, von unter her gesehen, das -te Quadrat, das
ganz in liegt. Die Anzahl der ganz in liegenden Quadrate im -ten
Streifen sei ; dann ist die RIEMANNsche Untersumme zu
gleich
Höhere Mathematik I SS 2007
h
=
$
$
=
=
Î
:
g
*
%
=
=
h
=
=
e
e
,
h

,
,
=
$
=
¸
5
m
q
:
J J
K
<
8
q
: ·
½
:
ì
;
q
:
$

$
:
ì
e
e

h
:
$
$
ñ
? $
@

$
$
e
? *
h
:

:
1
@
:
$
$
*
? 2

e
@

3
@
:

( )
=
()

h
@
h
h
@
0
1
e
2
2
()
.
Die Idee im Eindimensionalen ist bekanntlich, daß wir die Integrationsvariable als Funktion = ( ) einer neuen Variablen schreiben: Mit
= ( 0 ) und = ( 1 ) ist
w
=
,
Von den vielen Regeln zur expliziten Bestimmung einer Stammfunktion
ist sicherlich die Substitutionsregel die nützlichste; es lohnt sich daher, nach einer Verallgemeinerung dieser Regel für mehrdimensionale
Integrale zu suchen.
c) Die Transformationsformel
1
2
,
.
)
In diesen Beispielen hatten wir nur Kreisscheiben als Normalbereiche,
aber der Leser kann sich leicht überzeugen selbst davon überzeugen,
daß sich die Nützlichkeit dieser Mengen keineswegs auf solche trivialen Beispiele beschränkt: Man zeichne frei irgendeneinen beschränkten
zweidimensionalen Bereich auf ein Blatt Papier und überzeuge sich
davon, daß sich dieser durch Einfügen von (meist sehr wenigen) waagrechten und senkrechten Strecken als Vereinigung von Normalbereichen
der Typen I und II darstellen läßt.
1
:
=
$
2
e
1
2
:
1
@
2

zu
g
=
'
1
$
1
@
was durch die Substitution
=
1
h
2
(
1
e
@$
2
*
=

2
? 2
ûKûzÎ
:
h
1
:
2
2
$
=
$
'
so ist das innere Integral
:
2
(
1
h
2
2
:
1
úKúzÌ
2
Ë
1
*
2
e
? 1

=
1
2
Í
1
h
Schreibt man mit
=
ñ
2
2
$
$
1

2
JzJKJzJKJ
1
1
$
2
4 2
=
;
3
3
das Kugelvolumen als Volumen zweier Halbkugeln ist also in der Tat,
wie es sein soll, gleich 4 3.
1
1
2
)
. Somit ist das Volumen der Halbkugel gleich
3
=
2
:
1
(1
2
%
über
e
e
2
(1
$
=
:
3
1
2
Hierzu könnten wir eine dreidimensionale Integration durchführen, es
geht aber zum Glück auch einfacher: Natürlich genügt es, das Volumen
0 zu bestimmen, und dies ist die Menge aller Punkte
der Halbkugel
zwischen der Einheitskreisscheibe der (
)-Ebene und dem Graph
der Funktion
2
2
(
)= 1
1

2
? +
h
2
h
+
=
:
2
*
e
3
$
2
=
$
)
$
2
2
:
1
2
2
h
= (
und
1
1
Etwa interessanter ist die Berechnung des (hoffentlich auch bekannten)
Volumens der Einheitskugel
2
2
2 cos

2
2
2
*
e
? 1
h
2 1
wird, wie wir oben gerade nachgerechnet haben. Somit ist
Kap. 2: Mehrdimensionale Analysis
wie erwartet.
2
,
,
2
Wenn wir das Integral ganz rechts auf die linke Seite bringen, erhalten
wir den Flächeninhalt
Höhere Mathematik I SS 2007
h
Å

g
B

@
:
3
g
3
e
$
@
3
@
3
e
$
%
= (
und
= (
)
)
:
3 :
:
3 und
)
) = cos

:
:
h
e
e
:
ì
h
:
ñ
k
3
3
3
3
3
3

k
:
3
0
+
0)
¸
m
m
·
k
k

m
3
m
3
3
JzJ
3 :
3 þ
þ
:
3
:
k
(
3
3
:

þ
3
þ
0)
3
:
k
0
0)
0)
+ ( )
+ ( )
+ ( )
+ ( );
k
(
0
0)
ÿ
+
þ
0
3
+
3
(
0
+ ( )

0
(
ÿ
+ )= (
+
+
0)
+ ( )
k
0
0)
(
0
0
+ ( )
ÿ
ist natürlich im allgemeinen kein Rechteck, sondern eine krummlinig
begrenzte Figur; im Beispiel der Polarkoordinaten etwa wäre sie ein
Winkelbereich zwischen zwei Kreisbögen. (An den bei Polarkoordinaten etwas problematischen Nullpunkt als Ecke denken wir in diesen
Zusammenhang lieber nicht; es ist klar, daß sein Einfluß bei immer
3
+ )= (
þ
0
3
0
0
k
+
0
þ
(
0+
k
þ
und
(
3
3
0+
+
0)
0)
0
)
k
ÿ
) (
3
und
:
0
(
:
+ )= (
+
0)
0)
+ ( )

(
) aus diesem
k
þ
0
0
3
+ )= (
0
0)
Die Menge der Punkte (
), die zu den Punkten (
Rechteck gehören, d.h. also die Menge
0
(
0
ÿ
k
0
:
(
0
3
(
+ )
3
0
.
ì
þ
und somit den Flächeninhalt
:
+
:
k
k
0
3
und (
+ )
þ
0

3
0
+
0)
þ
3
(
= (
0)
:
0)
þ
3
+
0
:
+
(
0
3
3
0
+
0)

þ
(
0
3
= (
3
0)
3
ÿ
(
3
+
:
0
(
k
0)
)-Ebene
Trotzdem machen wir, wenn und differenzierbare Funktionen von
und sind, bei kleinen Rechtecken keinen allzu großen Fehler, wenn
wir die transformierte Menge als Parallelogramm betrachten, denn nach
Definition der Differenzierbarkeit ist
ÿ

0
ü T
þ

(
)-Ebene mit Bild in (
ý
kleiner werdenden Rechtecken für eine um den Nullpunkt beschränkte
Funktion immer kleiner wird.)
Abb. 75: Rechteck in (
P T
approximierten wir den Intgegrationsbereich durch kleine achsenparallele Rechtecke. Wenn wir statt über und über und integrieren,
müssen wir entsprechend den Bereich , in dem sich diese neuen Variablen bewegen, in achsenparallele Rechtecke zerlegen; dabei fordern
wir nun natürlich Parallelität zur - und zur -Achse. Wir betrachten ein
festes dieser Rechtecke; es habe die Eckpunkte
.
Ç
(
= (
Kap. 2: Mehrdimensionale Analysis
Zur Definition des Integrals
) = sin
3
= (
zweier neuer Variabler und . Ein wichtiges Beispiel, das man zur Veranschaulichung während der folgenden Rechnungen im Kopf behalten
sollte, ist die Polarkoordinatensdarstellung
)
(
Beginnen wir der Anschaulichkeit halber mit einer Funktion
zweier Veränderlicher und schreiben wir diese als Funktionen
Genauso können wir auch bei einer Funktion mehrerer Veränderlicher
diese als Funktionen neuer Variabler schreiben.
Höhere Mathematik I SS 2007
ÿ
þ
Höhere Mathematik I SS 2007
k

ÿ
þ
þ
Ë
Í
3
Ë
þ
3
0)
þ
þ
:
:
3
3
þ
þ
3
e
Î
Ì
k
ÿ
Î
e

<
ñ
JKJKJKJ
3
:
þ
þ
þ
þ
þ
þ
þ
J JKJKJ
K
k

:
$þ
3
( + )2
1
2
sin )
= ,
2
=
2
+
1
2
2
.
ì

1
k
1
ì
ì
ì
<
ì
=
h
m
Ë

ì
1
<
3 ìE
h
e
:
<
ìE
h

e
= e
Ì
h
h
e
3 :
3 :
ì
ì
0
und
Í
0
=
0
2
2
2
2
;
=
2
.

ñ
:
e
ñ
Im Vergleich zum letzten Abschnitt, wo wir das Integral (für = 1) in
2
kartesischen Koordinaten ausrechneten und dazu die Funktion 1
integrieren mußten, ist diese Rechnung erheblich einfacher; die Transformationsformel leistet also genau das, was wir von einer verallgemeinerten Substitutionsregel erwarten: Bei geschickter, an das Problem
angepaßter Substitution kann sie die Berechnung eines Integrals erheblich vereinfachen.
0
2
=
JKJ

ist also
m
die Fläche von
·
= (
) 0
Mit dieser Formel können wir beispielsweise noch einmal die Fläche
eines Kreises ausrechnen: Die Punkte der Kreisscheibe mit Radius
um den Nullpunkt haben Polarkoordinaten (
) im Rechteck
Wenn und simultan gegen null gehen, können wir
gegenüber
vernachlässigen,
des Rechtecks aus der (
)-Ebene wird also im wesentlichen nur
der Flächeninhalt
mit multipliziert – genau wie es die obige Rechnung auch zeigt.
1
2
h
h
3 þ
:
3 1

3 e
e
e
3
h
JzJKJzJ
3
:
þ
þ
þ
þ
:
3
þ
þ
J JKJzJ
z
3 $þ
h
h
:
3 1
e
ñ
:
:
ñ
Für unbeschränkte Integrationsbereiche stehen hier natürlich uneigentliche Integrale; da diese – so sie existieren – Grenzwerte von üblichen
Integralen sind, ist dies kein Problem.

:
.
h
m
)

:
= e
) (
þ
h

(

h
=
$þ
)
e
(
:
e

bijektiv ist, so gilt
þ
)
$
(
þ

¸
)

(

)
þ
þ
h

(
:
h
5
;
þ
Transformationsformel: :
sei eine integrierbare Funktion auf
2
, und die Variablen
seien als differenzierbare Funktionen
= (
) und = (
) neuer Variabler
dargestellt. Ist dann
2
ein Integrationsbereich, für den die Abbildung
sin ) sin

Der gesamte Integrationsbereich wird approximiert durch die Vereinigung der Parallelogramme zu den sämtlichen Rechtecken, mit denen
approximiert wurde; wenn wir also davon ausgehen, daß die Koordinatentransformation zwischen und und
bijektiv ist und wenn wir
– was eigentlich noch durch genauere Abschätzungen zu rechtfertigen
wäre – auch davon ausgehen, daß wir die oben erwähnten Fehler beim
Grenzübergang
0 und
0 vernachlässigen können, erhalten wir
die

( cos
(

=
$
( cos )

)
:
(

= cos
Für diese Formel hätten wir eigentlich nicht den ganzen Apparat der Transformationsformel gebrauch; Abbildung 75 zeigt uns, wie wir die Fläche des Bilds eines Parallelogramms
exakt ausrechnen können: Variiert zwischen und + und zwischen und + ,
)-Ebene als Bild die Differenz zwischen zwei Kreissektoren
so erhalten wir in der (
mit Öffnungswinkel und Radius + beziehungsweise ; der Flächeninhalt ist also
d.h.
der Polarkoordinaten ist

0
.
= sin

Der Flächeninhalt eines Parallelogramms ist bekanntlich gleich dem
Produkt der Kantenlängen mal dem Sinus des eingeschlossenen Winkels; falls wir die beiden Vektoren in den 3 einbetten, indem wir ihnen
eine Null als dritte Komponente geben, ist das gerade gleich dem Betrag
des Vektorprodukts, das hier nur in der dritten Komponenten von null
verschieden ist; die Fläche des Parallelogramms ist also

Ì
þ
(
Í
0)
0)
0
und

0
þ
(
= cos
(
und
3
0
Im Fall
(
0)
wenn wir Terme der Größenordnung ( ) und ( ) vernachlässigen, ist
die transformierte Menge also ein Parallelogramm mit Kantenvektoren
Kap. 2: Mehrdimensionale Analysis
? $
"
h
*
)
e
"
^
*
)
h
e
e
h
h
)
Ì
"
"
)
e
Ë
õ
"
:
Î
h
*
"
e
:
"
*
^
:
h
Í
h
e
)
"
Ì
"
:
Î
*
^
)
e
"
h
)
e
"
^
:
e
)
"
ì
x
<
3 <
e
e
e
3
þ
h
r

Í
h

e
h
r
h
h
h
)
Î
)

= e
Ì

)
e
ñ
:
*
õ
r
)
)
(
)
3
Í
ûzÎ
þ
3
Ë
3
)

h
þ
úzÌ
:
)
h
:
þ
þ
3

e
Den Flächeninhalt eines Parallelogramms mit Kantenvektoren
können wir auch wie folgt ausrechnen:

)
r
r $
r
.

ûzÎ
und
Ï
+
(
Ë
þ
ú Ì
z
þ
2
1
1
2
Ë
"
þ
ist. Diese können wir uns auch geometrisch veranschaulichen, denn sie
ist ja gerade der Flächeninhalt des Parallelogramms mit den Kantenvektoren
( 0 0)
( 0 0)
und
.
( 0 0)
( 0 0)
)
3
=
) (
2
.
Í
folgt sofort, daß
(
des Koordinatenwechsels
þ
3
ist leicht zu finden:
ñ
3 2
e
3 :
Die Stammfunktion des neuen Integranden
Aus
2
2
= 2
=
3
h
JKJKJKJ
3
:
þ
þ
þ
þ
0
:
0
1
2
überall positiv ist, folgt
0
2
2
:
Ë
þ
ú Ì
K
þ
.
3
:
2
h
þ
þ
=
:
ûKÎ
2
h
=
ñ
þ
þ
)
e
2
Í
+
e
gerade gleich der Determinanten der JACOBI-Matrix
3 þ
2
(
(
e
3
2
=
.
"
=
Í
3
$þ
=
h
þ
þ
J JKJKJ
K
3 :
2
"
þ
:
2
Ë
$þ
)
:
(
þ
þ
2
þ
þ
=
=
3
2
in der Formel
þ
2
2
=
þ
=
[0 2 ); also
In Polarkoordinaten entspricht 2 dem Bereich
0
ist das betrachtete Integral nach der Transformationsformel auch gleich
<
h
=
^
:
2
)
^
2
+
"
2
e
Zur Verallgemeinerung der Transformationsformel auf höhere Dimensionen beachten wir zunächst, daß der Term
)
(
=
*
þ
=

)
)
h
2
Î
"
+

?
2
Ì
^
(
)
und, da der Integrand von
0

Durch Grenzübergang können wir auch auch auf das unendliche Recht”
eck“ 2 als Normalbereich auffassen; daher ist
= e
5
Man kann zeigen, daß die Stammfunktion von
nicht in geschlossener Form durch elementare Funktionen ausdrückbar ist; Integration
mittels Stammfunktion ist also zwecklos. Stattdessen benutzen wir folgenden Trick:
e
=
r
h

2
Í
2
"
$
Also ist
h
.
2
" JKJKJKJ
r
=
= e
0
1
2
h
def
=
2
h
0
2
= e

0
Ë
2
Damit können wir weiterrechnen und erhalten das Ergebnis
Kap. 2: Mehrdimensionale Analysis
2
Als nächstes Beispiel wollen wir endlich einmal ein Integral ausrechnen, bei dem wir das Ergebnis nicht besser und viel einfacher durch
elementargeometrische Überlegungen bekommen können: das Integral
Höhere Mathematik I SS 2007
%
Ï B
@
)
h
)

$
Ï
Ï )
Ï )
B
@
<
@
B
@
Ï B
Ï @
B
Ï )
B
Ï B
Ï
Ï B
ìE
Ï B
@
Ï )
B
5
5
3
)
Ï B
Ï
ì
=

1
Ï )
Ï )
Ï )
B
Ï B
Ï @
@
B
@
B
@
e
e
e
e
h
5
h
ñ
\
ñ

$
3 e
e
e
Ï
Ï B
Ï @
)
h
h
Ï B
@
Ï B
Ï @
det
)
=
(
)
3 q
q
þ
q
: þ
ñ
:
þ
þ
þ
Ë
þ
3
þ
þ
3 (
)
3 :
h
(
(
)
schreiben, zu
(
ein Integrati-
, wenn wir kurz
<
def
) =
\
3
2
( )
{ æ
(
\
( ) det
1
G
Ausgeschrieben wird die Formel für den
1
;
ìE
( )
ì
bijektiv ist, so gilt
3
( )
dargestellt. Ist dann
neuer Variabler 1
onsbereich, für den die Abbildung
<
5
1
h
h
:
þ
:
þ
Ï
þ
Ï
@
þ
e
e
e
@ 5
5
5
Ï
Ï
).
5
G
3
:
q
þ
þ
þ
ú úKúKúzÌ
K
@
1
3
.
det(
5
h
3
Genauso können wir auch in höheren Dimensionen argumentieren:
Durch mehrfache Scherung läßt sich ein beliebiges Parallelepiped in
einen Quader überführen; das Volumen des von
Kantenvektoren
aufgespannten
Parallelepipeds
ist
also
gleich
1
)
<
3
multipliziert. Da deren Determinante gleich eins ist, ändert sich dabei
nach dem Multiplikationssatz für Determinanten nichts am Wert von
det( ). Der Flächeninhalt eines von den Vektoren und aufgespannten Parallelogramms ist also stets gleich det( ), egal bezüglich welcher
Orthonormalbasis die Kantenvektoren dargestellt werden.
ì
5
h
Beim Übergang zu einem anderen orthonormalen Koordinatensystem
werden die Koordinatenachsen gedreht, d.h. sie werden mit einer Matrix
der Form
cos
sin
sin
cos
5
1
5
).
3
3
= det(
5
(
5
1
sei eine integrierbare Funktion
seien als differenzierbare
5
=
0
3
= det
<
..
.
1
1
Im allgemeinen wird das Parallelogramm natürlich kein Rechteck sein;
da die Basisvektoren im Gegensatz zu und aufeinander senkrecht stehen, müssen wir dann als Linearkombination = 1 + 2 schreiben.
Dabei können wir 2 als Projektion von auf die von 2 aufgespannte
Koordinatenachse auffassen. Da sich das Parallelogramm durch Scherung in das Rechteck mit Kantenvektoren und 2 überführen läßt und
sich der Flächeninhalte bei Scherungen nicht ändern, hat das Parallelogramm immer noch den Flächeninhalt
@
Ï B
0
<
Transformationsformel: :
auf
, und die Variablen
Funktionen
1 = 1(
@
).
@
= det(
Ï
0
x
die
Ï
Damit gilt also im
@
= det
Ï
(Für = 3 kennen wir diese Formel bereits, denn wir wissen, daß dort
das Volumen gleich dem Spatprodukt ( 1
2)
3 der drei Vektoren
ist, und dieses wiederum ist gleich der Determinanten.)
Kap. 2: Mehrdimensionale Analysis
Das (kartesische) Koordinatensystem in 2 sei so gewählt, daß der
Vektor ein Vielfaches 1 des ersten Koordinateneinheitsvektors ist.
Falls dann auch noch = 2 ein Vielfaches des zweiten sein sollte,
falls also das Parallelogramm sogar ein achsenparalleles Rechteck sein
sollte, ist dessen Fläche gleich
Höhere Mathematik I SS 2007
.
3
h
JzJKJKJKJKJKJzJKJKJ
Í
ûKûKûKûzÎ
q
þ
q
þ
þ
3
JzJKJKJKJKJKJzJKJKJ
3 ñ
@ 5
5
5

:
sin sin
cos sin
0
cos cos
sin cos
sin
q

*
Ë
$

*
*

Í
Î

r
r

JKJKJKJ

JKJKJKJ
$
JKJKJKJ

$
JKJKJKJ

$
G
G

e
e
e
h
h
G

h
h
h
e
e
e
ñ
q
:
q
: ñ
ì
e
e
e
h
h
= e

= e
Ì
Ì
h
:
ñ
Ë
sin

0
G
Î
= e
q
G
=
3
.
Í
h

= e
2
2
+
:
2
2
+
2
2
=1
einführen und damit das Volumen des Ellipsoids
= cos
= sin sin
q
Ì
0
e
Î
0
h
3
h

=
h
sin
Í
q
3
Í
=
Ë
Ë
G
3
4
:
3
2
B
3
q
2
@
0
ñ

0
:
0
q
sin

2
q
,
Genauso lassen sich auch beliebige andere Koordinatensysteme behandeln, beispielsweise könnte man zum Rechnen mit einem Ellipsoid auch
Ellipsoidkoordinaten
= cos sin
)
)
sin
(

=
,

2
0
0
1
q
Berechnen wir zur Kontrolle schnell noch einmal das Volumen der Kugel
um den Nullpunkt mit Radius :
e
sein soll.
.
sin
e
2
:
)
q
(
e
=
h
)
ñ
) = ( cos
h
(
h
(
=
e
wobei wieder
)
e
cos )
(
wird die Transformationsformel zu
q
sin sin

) = ( cos sin

h
(
þ
h
und mit
:
q

þ
þ
þ
ú úKúKúzúKÌ
z

h
sin
þ
2
q
sin .
þ
Der Betrag der Determinanten der JACOBI-Matrix ist also

2
Ë
þ
=

:
2
þ
þ
sin

sin
þ
þ
2
q
cos (sin cos )
þ
þ
2
ûzûKûKûzûKÎ
:
q
q
q
þ
þ
þ
þ
und die Determinante davon ist wie bei den ebenen Polarkoordinaten
gleich . Also haben wir hier im wesentlichen dieselbe Transformationsformel wie bei den ebenen Polarkoordinaten (Zylinderkoordinaten
sind schließlich im wesentlichen auch nichts anderes als ebene Polarkoordinaten), nämlich

=
þ

sin sin
cos sin
q

cos sin
sin sin
Í

sin
$
cos cos
sin cos
sin
cos
0
<

sin sin
cos sin

cos
sin
0
auch noch Zylinderko-

cos
q
=
und
3

Entwicklung nach der dritten Zeile ergibt für die Determinante den Wert
:
.
also
= ,

die JACOBI-Matrix ist also
cos sin
= sin sin
cos

= sin
= cos

= cos
,
= sin sin
Außer den Kugelkoordinaten hatten wir im
ordinaten betrachtet; für diese ist
Kap. 2: Mehrdimensionale Analysis
Als Beispiel können wir wieder Koordinatensysteme betrachten: Für
Kugelkoordinaten ist
= cos sin
Höhere Mathematik I SS 2007
B
@
h
h
Î
G
= e
4
3
B
@
2
d) Der Satz von Green und der ebene Satz von Gauß
In Physik und Technik sind noch zahlreiche weitere bewährte Koordinatensysteme im Einsatz, auf die wir hier nicht eingehen können; dank der
obigen Transformationsformel kann man immer das benutzen, das der
jeweiligen Situation am besten angepaßt ist und mithin am wenigsten
Rechnung verlangt.
.)
ì
<
sei ein Bereich, dessen Rand aus endlich vielen Kurvenstücken
bestehe. Dann können wir sowohl über als auch über dessen Randintegrieren; die beiden Sätze in diesem Abschnitt befassen
kurve
sich mit der Beziehung zwischen diesen beiden Integrationen.
ì
ë
þ
ì
ì
©
ì
ì
©
©
Für eine geschlossene Kurve dagegen erwarten wir, wenn wir uns von
der Anschauung leiten lassen und uns die Kurve als eine Art deformierten
Kreis vorstellen, daß sie die Ebene in zwei Bereiche zerlegt: einen
beschränkten Bereich
und einen unbeschränkten Bereich . Hier
sollten sich und gegenseitig so stark beeinflussen, daß eigentlich
auch die Integration über
etwas mit der Integration über zu tun
haben müßte.
ì
ì
©
©
ì
ì
ì
©
Jordanscher Kurvensatz: sei eine geschlossene ebene Kurve ohne
zwei Zusammenhangskomponenten,
Überkreuzungen. Dann hat 2
von denen die eine beschränkt und die andere unbeschränkt ist.
ë
MARIE ENNEMOND CAMILLE JORDAN (1838–1922) leistete wesentliche Beiträge zur Entwicklung der Topologie und der Gruppentheorie. Er beschäftigte sich auch
mit der Lösbarkeit nichtlinearer Gleichungen und stellte in einem vielbeachteten Buch die GALOISsche Theorie über die Nichtlösbarkeit allgemeiner Gleichungen
vom Grad größer vier dar. Seine Untersuchungen über
endliche Körper führten ihn zu der heute als JORDANZerlegung bekannten Darstellung von Matrizen, mit der
wir uns im nächsten Semester beschäftigen werden;
außerdem bewies er Satze über die Konvergenz von
FOURIER-Reihen.
2
Satz von Green:
sei eine abgeschlossene Menge, die sowohl
als Vereinigung endlich vieler Normalbereiche vom Typ I wie auch
als Vereinigung endlich vieler Normalbereiche vom Typ II geschrieben
werden kann; ihre Randkurve sei so orientiert, daß im Gegenuhrzei1
2
gersinn umlaufen wird. Weiter sei
(
) ein differenzierbares
Um den JORDANschen Kurvensatz zu umgehen, starten wir einfach mit
2
, von dem wir all das verlangen, was uns nacheinem Bereich
her das Leben einfach macht; in der Praxis sollte es (hoffentlich) selten
schwierig sein, diese Forderungen für die Bereiche aus konkreten Anwendungen zu verifizieren.
<
Nun ist es natürlich etwas gefährlich, sich nur von der Anschauung leiten
zu lassen, denn es gibt sicherlich erheblich mehr Kurven, als man sich
gemeinhin vorstellt. Beispielsweise gibt es auch Kurven, die wie eine
Ziffer 8 aussehen, etwa die Lemniskate, und diese zerlegen die Ebene
in drei Bereiche. Wir müssen also noch zusätzlich fordern, daß sich die
Kurve nicht selbst überkreuzt, aber dann gilt in der Tat
©
Im allgemeinen kann man natürlich nicht viel erwarten: Nimmt man
aus
eine Kurve heraus, ist es bei der Integration einer stetigen
Funktion gleichgültig, ob man über oder über
integriert, das
Randintegral ändert sich aber um das im allgemeinen nicht verschwindende Kurvenintegral über .
©
Der Beweis dieses anschaulich fast selbstverständlichen Satzes erfordert einen erstaunlich großen Aufwand: Man muß die Ebene in kleine
Quadrate (oder Dreiecke oder etwas ähnliches) unterteilen, durch Kantenzüge aus deren Seiten annähern, den Satz durch aufwendige Rechnungen mit formalen Summen von Quadraten und Quadratseiten für
die angenäherten Kurven beweisen und dann schließlich noch durch ein
Limesargument zeigen, daß die Aussage auch für selbst gilt. Die genaue Durchführung dieses Beweises würde etwa drei Vorlesungstermine
erfordern – ein Aufwand, der für uns in keinem vernünftigen Zusammenhang mit seinem Nutzen steht: Bei den meisten in der Praxis vorkommenden Kurven wird die Aussage des JORDANschen Kurvensatzes
zumindest für diese speziellen Kurven ohnehin klar sein.
Kap. 2: Mehrdimensionale Analysis
bestimmen. (Die Antwort ist natürlich (?)
Höhere Mathematik I SS 2007
ì
<
D Ò
Ï Ð
8
©
<
ì
ë
©
©
<
ì
.
D
þ
Ð
þ
e
Ð
h
ÑÏ Ð
h
h
þ
$þ
e
e
:
:
ñ
Ô
·
ÏÓÐ
ì
B
m
m
@
JKJ
<
8
:
:
÷
<
B
©
@
1
B
B
y
©
<
1
B
©
@
@
1
<
y
©
@
@
Í
h
Ë
¥
þ
* e
úKÌ

1
Ð
e
h
e
h
.
e
g
Ð
e
()
w
þ
Ð
1
Ð
g
w
g
w
Ï Ð
Ô
e
h
e
Ð
Ð
h
Ï Ð
1
ö
'
=
$þ ( )
1
:
1
()
()
4
.
( )
1
( )
.
Damit gilt er aber zumindest für dieses spezielle Vektorfeld auch für
jeden Bereich , der sich in Normalbereiche vom Typ I zerlegen läßt:
Das Flächenintegral über ist gleich der Summe der Flächenintegrale
über die Normalbereiche vom Typ , in die wir zerlegt haben und somit
Zumindest für das hier betrachtete spezielle Vektorfeld
ohne Komponente und einen Normalbereich vom Typ I ist der Satz also
richtig.
=
2
()
1
y
1
()
:
$
1
1
3
y
e
3
1
:
()
1
þ
Ð
Ð
0
y
=
:
1

:
=
<
und entsprechend
1
þ
Ð
1
1

0
þ
Ð
e
=
B ÷
h
1
()
÷
Da Normalbereich vom Typ I ist, können wir auch das Flächenintegral
über leicht ausrechnen:
Ô
(
()
g
h
1
e
h
È
w
, also
w
Ð
$
)=
g
'
e
1(
e
þ
Dann ist

$
þ
Ð
1
( )
h
schließlich die linke Seitenstrecke.
y
h
;
()
h $
Ð
2
h
( ) ( )
4:
4.
, also ist
die obere Begrenzungskurve, und
e
Ð
1
g
()
;
()
1
2
Ô
=
w
2
)
=
1
+
h $
ÏÑÐ
y
]
©
e
Ð
(
=
(
3: [
w
die rechte Randstrecke,
m
:
h $
Ï Ð
h
;
y
h
Ï Ð
2
m
e
Ô
( ) ( )
Ô
2:
¸
Ï Ð
sei die untere Begrenzungskurve,
= 0,
0
1
Wenn wir im Gegenuhrzeigersinn um herum integrieren, werden die
Kurvenstücke 3 und 4 rückwärts durchlaufen, also ist
©
e
()
Ô
©
h
ÑÏ Ð
;
e
]
e
h
ÏÑÐ
und genauso folgt auch das Verschwinden des Integrals über
g
÷
Ô
1: [
¥
h
2
e
e
berechnen wir am besten
Ð
e
voraus. Das Integral über die Randkurve
komponentenweise:
( )
ög
( )
Å©
@
und
)
= (
0
1
)=
©
2
)
h
0
=
4(
0
1
Å©
1(
)=
( )
2(
Beweis: Wir betrachten zunächst nur ein Vektorfeld = 01 mit verschwindender -Komponente und setzen als Normalbereich
2
=
( )
Für die beiden Seitenstrecken ist
1
. Dann ist
2
2
Kap. 2: Mehrdimensionale Analysis
=
von
<
Vektorfeld auf einer offenen Teilmenge
Höhere Mathematik I SS 2007
ì
^
ì
ì
h
y
g
h
y
g
Ô
problemlos. Die Randkurve von besteht einerseits aus Kurvenstücken,
die auch zum Rand von gehören, andererseits aus solchen, die durch
die Zerlegung eingeführt wurden und zwei Normalbereiche voneinander
trennen. Letztere werden aber als Randkurven der beiden angrenzenden
Normalkurven jeweils in entgegengesetzter Richtung durchlaufen, so
daß sich die Integrale längs solcher Kurvenstücke gegenseitig wegheben.
Summiert man also die Integrale über die Ränder aller Normalbereiche
auf, bleiben am Ende nur die Integrale längs jener Kurvenstücke übrig,
die auf der Randkurve von liegen, die Summe ist somit gleich dem
Integral über die Randkurve.
Höhere Mathematik I SS 2007
ì
e
ì
ì
(
:
$þ o
ñ
:
Ï Ð
Ï Ð
©

Ô
Å©
,
Ô Ô
Ï
=
und
=
Ï
þ
Å©
$
erhalten wir somit den
Å©
2(
)
(
1 )
grad
Der erste Vektor im Integranden der dritten Zeile ist einfach der Gradient
von . Der zweite Vektor hat Skalarprodukt null mit dem Tangentenvektor ( ) = 12 (( )) , steht also auf diesem senkrecht und ist somit ein
Normalenvektor. Das Skalarprodukt des Gradienten einer Funktion mit
einem Vektor ist bekanntlich die Richtungsableitung der Funktion in
Richtung dieses Vektors; mit
.
2(
wird zu
2(
2)
()
()
)+
Å©
1(
1(
1
2
h
()
2
)
Å©
=
=
)
2( )
Å©
()
+
=(
©
()
2
þ
Das Integral über die Randkurve
bezeichnet.
o
=
2
wie üblich den LAPLACE-Operator
+
)
:
GEORGE GREEN (1793–1841) war der Sohn eines Bäckers aus Nottingham. Er besuchte nur von 1801 bis 1802 eine Schule, danach arbeitete er in der Bäckerei und später
in der dazugekauften Mühle. Es ist nicht bekannt, wann und wie er Mathematik lernte.
1827 veröffentlichte er sein Buch An Essay on the Application of Mathematical Analysis to the Theory of Electricity and Magnetism, von dem 51 Exemplare verkauft wurden,
größtenteils in Nottingham selbst. Einer der Leser stellte Kontakte zur Cambridge Philosophical Society und zur Royal Academy in Edinburgh her, so daß GREENs weitere Arbeiten
(über Elektrizität und über Hydrodynamik) dort veröffentlicht wurden. 1833 begann er
mit dem Studium der Mathematik an der Universität Cambridge; nach dessen Abschluß
blieb er in Cambridge, bis er 1840 wegen gesundheitlicher Probleme nach Nottingham
zurückkehrte. Weder GREEN selbst noch seine Zeitgenossen erkannten die Bedeutung
seiner Arbeiten, die, in heutiger Sprechweise, Potentialfunktionen einführten und für die
e
(
schreiben, und der Satz gilt für beide Summanden. Da beide Seiten der
Behauptung linear in sind, folgt der Satz auch für selbst.
Ð
:
þ
©
)
þ
þ
ñ
wobei
e
©
0
þ
Ð
*
:
2(
*
þ
+
Ï Ð
þ
)
:
h

0
h

1(
=

*
e
)
)
$
ñ
2(
:
=
h
1(
1
8
:
)=
2
h
(
2
D (
einsetzen, erhalten wir für das Flächenintegral
mit
o
läßt
)
)
:
e
Der Rest des Beweises ist nun einfach: Ein beliebiges Vektorfeld
sich als Summe
(
(
Ò
)=
<
e
Als nächstes beweisen wir ihn für Vektorfelder mit verschwindender
-Komponente; wenn man mit Normbereichen vom Typ II argumentiert
statt mit solchen vom Typ I, kann man dazu die obigen Argumente fast
wörtlich wiederholen.
(
Ï Ð
speziell ein Vektorfeld der Form
h
mit verschwindender
Wenn wir für
h
Damit ist der Satz bewiesen für alle Vektorfelder
-Komponente.
Physik nutzbar machten. Auf dieser Grundlage bauten später JAMES CLERK MAXWELL
(1831–1879) und andere die Elektrodynamik auf.
Kap. 2: Mehrdimensionale Analysis
%
.
wie im Satz von GREEN
©
h
D
e
<
D Ò
8
e
e
þ
o
ì h
:
h
ñ
Ô
:
<
1
ì
q
3 1

3 3 ë
k
(
8
0)
ì

k
+
(
3
ì
3
0
0)
+
k
3
0
2
+
2
k

4
ÿ
4
3

k
3
ì
8
3
Da hier nur und variabel sind, bedeutet die Forderung nach zwei linear unabhängigen Tangentialvektoren, daß die beiden Vektoren ( 0 0 )
und ( 0 0 ) in allen Punkten ( 0 0 )
linear unabhängig sein
müssen.
0) +
0
)= (
0+
ì
0+
<
3
?
(
3
<
<
B
@
Definition: Ein reguläres Flächenstück im 3 ist gegeben durch einen
2
differenzierund eine in einer offenen Menge
Bereich
3
baren Funktion :
)
(
), für die gilt:
; (
1.) Die Einschränkung
von auf ist injektiv.
ist ( 0 0 )
( 0 0 ) = 0.
2.) In jedem Punkt ( 0 0 )
An dieser Stelle führt die Beschränkung auf den 3 zu einer kleinen
Vereinfachung: Im 3 , und nur dort, existiert ein Vektorprodukt; zwei
Vektoren sind genau dann linear unabhängig, wenn dieses Vektorprodukt
ungleich dem Nullvektor ist. Sowohl der Betrag als auch die Richtung
dieses Vektors werden uns schon bald in mehrfacher Hinsicht nützlich
sein; wir definieren daher
Ï
ì
<
1
<
1
<
ì

3 ñ
D
ì
ë
<
1
©
Å©
.
Dí
3
3 3
x
3
4
ì
8
Die wichtigste Oberfläche, mit der wir es im folgenden zu tun haben
werden, ist die der Kugel. Die Oberfläche einer Kugel vom Radius
hat in Kugelkoordinaten die Gleichung = mit beliebigen Winkelkoordinaten und , sie ist also (in kartesischen Kordinaten) gegeben
.
Die Vorgehensweise bei der Definition eines Oberflächenintegrals entspricht genau der bei der Definition des Kurvenintegrals: Dort hatten wir
definiert; hier definieren
Kurvenstücke als Funktionen : [ ]
wir entsprechend Flächenstücke durch Funktionen zweier Parameter.
Wir müssen dabei allerdings etwas sorgfältiger vorgehen, denn im Vergleich zum Kurvenfall ist die Situation zumindest in zweierlei Hinsicht
komplexer: Erstens gibt es auf der reellen Geraden im wesentlichen nur
eine Art von zusammenhängenden Teilmengen, nämlich die Intervalle. In der Ebenen gibt es erheblich mehr Möglichkeiten – aber damit
hatten wir uns ja schon bei der Definition von Flächen- und Volumenintegralen beschäftigt. Zweitens mußten wir bei Kurven nur fordern, daß
( ) nirgends verschwindet, um die Existenz eines Tangentenvektors
zu garantieren. Hier im Zweidimensionalen recht das nicht mehr: Ein
Flächenstück hat in jedem Punkt Anspruch nicht nur auf eine Tangente,
sondern auf eine ganze Tangentialebene; wir müssen also sicherstellen,
daß es in jedem Punkt mindestens zwei linear unabhängige Tangentenvektoren gibt.

3 Im dreidimensionalen Fall wird der Satz von GAUSS, wie die meisten
wohl bereits aus der Physik wissen, ein Volumenintegral mit dem Fluß
durch eine Oberfläche in Verbindung bringen. Was Volumenintegrale
sind, haben wir inzwischen auch hier definiert; in diesem Abschnitt
geht es um den Begriff des Oberflächenintegrals, um den Fluß eines
Vektorfelds durch eine Oberfläche und um verwandte Themen.
3 2
auf einer Teilmenge
; mit Blick auf unsere Erfahrungen bei
Kurvenstücken wollen wir von vornherein fordern, daß differenzierbar
sein soll in einer offenen Umgebung von . Für kleine reelle Zahlen
ist dann für einen Punkt ( 0 0 )

e) Oberflächenintegrale
<
Ein Flächenstück soll demnach gegeben sein durch eine Funktion
(
)
3
:
)
(
)=
(
)
; (
(
)
<
Mit einer Verallgemeinerung sowie auch mit der anschaulichen Interpretation dieses Satzes werden wir uns in Abschnitt f) noch genauer
befassen.
Die dazu notwendigen Definitionen kann man problemlos für Flächenstücke in jedem
hinschreiben; wir wollen uns aber, da dies für alle
hier betrachteten Anwendungen ausreicht, auf den etwas anschaulicheren Fall von Flächenstücken im 3 beschränken.
=
und
Kap. 2: Mehrdimensionale Analysis
Satz von Gauß (ebener Fall): Für
2
2
(
) gilt
und
Höhere Mathematik I SS 2007

1
<
1
cos sin
3
sin sin
; (
: [0 2 ) [0 ]
)
.
cos
Die Differenzierbarkeit ist hier überhaupt kein Problem: Die angegebene
Funktion ist sogar auf ganz 2 beliebig oft stetig differenzierbar.

<
x
Bei der Injektivität gibt es allerdings Probleme: Für = 0 und =
ist sin = 0; daher werden alle Parameterpaare ( 0) auf (0 0 ) und
aller Parameterpaare (
) auf (0 0
) abgebildet.
$

.
8
8
Die partiellen Ableitungen von sind
sin sin
cos sin
=
und
0
also ist
2
cos sin2
2
=
sin sin2
2
sin cos

$
@
ì
1
$
Í

Ë
<
B

Ì
x

A
;
() () .
3
1
<

6 6
3
6
4 6
4
Der Betrag des Vektors
() ()
+
() ()
ist gleich
der Wurzel aus dem Skalarprodukt des Vektors mit sich selbst, also der
()
=
Wir wollen natürlich, daß diese Kurve immer dieselbe Länge hat, egal
ob wir sie einfach so im 3 oder auf einem Flächenstück betrachten.
Die Länge des Kurvenstücks auf dem Flächenstück ist daher gleich
der bekannten Länge des Kurvenstücks im 3 , also
3
<
]

wird dann beschrieben durch die zusam-
3
:[
3
1
=
die eigentliche Kurve im
mengesetzte Abbildung
() () ;
Für die meisten praktischen Zwecke ist das natürlich völlig unproblematisch: Bei der Flächenbestimmung oder allgemeiner der Integration
einer beschränkte Funktion sind einzelne, isoliert liegende Punkte irrelevant. Lediglich im Falle von uneigentlichen Integranden muß man
B
Somit können wir die Kugel nur dann als reguläres Flächenstück auffassen, wenn wir die beiden Pole herausnehmen, d.h. wenn wir uns auf
den Parameterbereich [0 2 ) (0 ) beschränken.
A
Da für eine echte Kugel
0 sein muß und (
) die Länge hat,
ist dieser Vektor genau dann gleich dem Nullvektor, wenn sin = 0 ist;
wie bei der Injektivität gibt es also wieder Probleme an den Polen, aber
auch nur dort.

]
1
).

:[
ì
(
;
Wir beschreiben eine Kurve auf einem Flächenstück :
durch eine Funktion
<
sin
,
=
cos cos
sin cos
sin
=
Das ist aber glücklicherweise auch bereits alles was passieren kann, denn
falls sin = 0 ist, können wir aus der dritten Komponenten cos den
Winkel
[0 ] eindeutig bestimmen. Damit kennen wir auch sin
und bekommen aus den ersten beiden Komponenten von den Cosinus
und den Sinus von , wodurch
[0 2 ) eindeutig festgelegt ist.
Längen sind Eigenschaften von Kurven; wir müssen also eine Kurve oder
– da wir Längen auch stückweise aneinandersetzen können – einfacher
ein Kurvenstück auf einem Flächenstück betrachten. Genau wie man etwa bei der Navigation auf der Erde nicht von einem dreidimensionalen
kartesischen Koordinatensystem ausgeht, sondern von der geographischen Länge und Breite, empfiehlt es sich auch hier, Kurven über die
Parameter des Flächenstücks zu definieren – und sei es auch nur, um
sicher zu sein, daß die Kurve auch wirklich auf dem Flächenstück liegt.
Nachdem wir nun wissen, was ein reguläres Flächenstück ist, müssen wir
als nächstes lernen, damit zu rechnen. Bevor wir uns an die Bestimmung
von Flächeninhalten machen, ist es vielleicht ganz nützlich (wenn auch
nicht unbedingt notwendig), daß wir uns ein paar Gedanken über die
Längenmessung machen.
hier sehr vorsichtig sein; hier in dieser Vorlesung sollen entsprechende
Integrale deshalb vorsichtshalber gleich gar nicht erst definiert werden.
Kap. 2: Mehrdimensionale Analysis
durch die Funktion
Höhere Mathematik I SS 2007
3
3
h
4
3
h
h
h
h
3
3
3
3
3
4
4
)=
3 3 3 Ú
)
×
(
(
)
)
(
4
3 (
3 3 3 3 3 und
sin

2
cos
×
+ sin
2
2
cos

2
+ sin
)=
2
.
,
3
x
4
e
ñ

sein, und genau das definieren wir auch als den Flächeninhalt eines
Flächenstücks.
ì
Dieses Ergebnis sollte man auch geometrisch interpretieren: Das Verund
also, bedeutet,
schwinden von , die Orthogonalität von
2
4
e G
(cos

( sin sin cos cos + cos sin sin cos ) = 0
also sollte die Fläche des Flächenstücks gleich
G
)=
$
)=
ì
h
(
sin
+ cos
h
2

sin
2

)=
4
(

(sin

x
2
)=
2

(

;

2
cos cos
sin cos
sin
k
2
=
k
G
2
2
und
Unser Hauptziel hier sind allerdings nicht Längenberechnungen, sondern die Berechnung von Oberflächen bzw. von Flüssen von Vektorfeldern durch diese Oberflächen. Dabei gehen wir genauso vor, wie bei
der Transformationsformel im vorigen Abschnitt: Wir unterteilen den
Parameterbereich durch Rechtecke, und betrachten deren Bilder auf
dem Flächenstück. Diese sind, da wir als differenzierbar vorausgesetzt
haben, in erster Näherung Parallelogramme, wobei die Näherung bei zunehmender Verfeinerung des Rechteckgitters auf immer besser wird.
Der Flächeninhalt eines solchen Parallelogramms mit Kantenvektoren
und
ist
G
also ist
sin sin
cos sin
0
=
Um etwas Übung im Umgang mit diesen Größen zu bekommen, wollen
wir sie für die Kugeloberfläche in ihrer oben angegebenen Parametrisierung berechnen. Hier ist, wie wir schon wissen,
als Fundamentalgrößen des Flächenstücks .
)
g
(
e
)=
Ú
(
?
),
Å3
(
)
Å3
(
2
Å
)=
Å
+
×
(
+2
h
berechnen; dem interessierten Leser sei empfohlen, damit beispielsweise überprüfen, daß Breitenkreise i.a. nicht die kürzeste Verbindung
zwischen zweien ihrer Punkte sind, sondern daß der Kreis um den Kugelmittelpunkt durch diese beiden Punkte (der sogenannte Großkreis)
eine kürzere Verbindungskurve liefert.
2
Allgemein kann man die Länge einer Kurve auf einem Flächenstück
somit als Integral
w
In dieser Formel können wir zwei Arten von Termen unterscheiden:
Rechts stehen jeweils die Ableitungen von und nach ; diese hängen
nur von der jeweiligen Kurve ab, die ja gerade durch die Funktionen
( ) und ( ) definiert ist. Links dagegen stehen Ausdrücke in den partiellen Ableitungen von nach und ; diese sind Funktionen auf dem
Flächenstück und sind insbesondere unabhängig von jeder Kurve. Wir
bezeichnen daher diese drei letzteren Größen
.
2
()
() ()
2
4
3
()
×
daß die Längenkreise und die Breitenkreise in jedem Punkt der Kugel
(außer den beiden Polen) aufeinander senkrecht stehen; die Konstans
von kommt daher, daß alle Längenkreise gleich lang sind, und die
-Abhängigkeit von schließlich reflektiert die Tatsache, daß die Breitenkreise verschiedene Radien haben.
Ú
+
() ()
h
() ()
()
2
h
+2
h
3
() ()
2
Kap. 2: Mehrdimensionale Analysis
Wurzel aus
Höhere Mathematik I SS 2007

h
h
G
e G
!
e
3
x
4
ñ
h
¥
!
!
<
1
ì
h
Í

Î
x
Ë
Ì
e
e
"'
%
h
Í

Î
h
= e
= e
Ì
ñ
( )
( )
6
$
%4
6
B
%1
( )
)
HI
=
(
( )
=
=
=
C
( )
-
( )
( )
)
( )
(
:
(
( )
( )
( )
,
( )
usw.
( )
( )
)
2
und die entsprechenden Funk-
.
,
.
und entsprechend für die anderen
(
( )
( )
)
)
7 '
" 1
7
7
%4
%1
%1
ist und dementsprechend
= (
E
)
(
3
'
" 1
E
'
"21
3
%4
0
3
0
%4
%1
"
$
#
det
#
det
.
Die Berechnung von Vektorprodukten ist etwas umständlich und sehr
anfällig für Vorzeichenfehler; wir wollen daher sehen, daß die Fundamentalgrößen einer Fläche ihrem Namen gerecht werden und uns auch
diese Berechnung abnehmen können: Der Flächeninhalt eines Parallelogramms mit Kantenvektoren und ist gleich dem Produkt der Längen
Damit folgt die Behauptung aus der Transformationsformel.
)
)
'
"24
(
3
= (
)
Entsprechendes gilt auch für die anderen Indexkombinationen, und nach dem Multiplikationssatz für Determinanten gilt eine entsprechende Produktbeziehung auch für die
Determinaten der hier stehenden Matrizen; insgesamt erhalten wir also, daß
also ausgeschrieben
(
G
6 '
" 1
B
'
"84
Ý
&#
%
Ý
"'
%
(
(
(
.
Nach der zweidimensionalen Kettenregel ist dann
6
HI
0
#
(
* ,
(
.
* +
-
)
(
(
.
=
)
7
E
G )
F
* ,
und
"
Aus
=
folgt, daß auch
Komponenten. Damit ist auch (
%
%
'
&#
$
* +
0
0
(
=
def
=
7'
F
G J
Beweis: Nach Definition ist
)
5
6
F
7 '
" 4
.
%
Analog dazu definieren wir auch Funktionen
tionen für .
"
"
'
6 '
" 4
=
(
7
3 seien zwei Flächenstücke, für die es eine in einer
und :
stetig differenzierbare Funktion gebe, die bijektiv auf
abbildet
ist. Dann ist
3
6
7
GKJ
0
3
" 1
E
"
5
C
G J
Lemma: :
Umgebung von
derart, daß =
"84
F
GKJ
Genau wie Kurvenintegrale sind auch Oberflächenintegrale unabhängig
von der Parametrisierung des Flächenstücks; im wesentlichen geht alles
genau wie bei den Kurvenintegralen, ist aber etwas aufwendiger. Der
Vollständigkeit halber sei die entsprechende Aussagen samt Beweis im
Kleindruck abgedruckt:
"
6
"
7
womit wir uns wieder einmal in hundertprozentiger Übereinstimmung
mit der Schulmathematik befinden.
" 1
"
5
,
5
" 4
#
2
6
%
"
( cos + cos 0) = 4
7
" 1 " 1
9;:
" 1
$
5
2
" 4
6
" 4
6
=2
5
" 1
5
und genau entsprechend natürlich auch für . Die links stehenden Determinanten sind
offensichtlich gerade die Determinaten der JACOBI-Matrizen der verschiedenen zweidimensionalen Projektionen von ; an der ersten Stelle etwa die der Funktion
<;=
Ý
0
9?>@>@>@>@>A>@>@:
" 1
0
5
" 4
" 1
B
sin
" 4
7
" 1
" 4
=
" 1
" 1
B
6
sin
( )
6
" 4
2
6
" 4
C
2
7
( )
<?D@D@D@D@DAD@D@=
2
7
( )
cos sin2
=
= sin
(
);
sin sin2
2
sin cos
die Länge dieses Vektors ist also, da (
) als Radiusvektor natürlich
die Länge
haben muß, gleich 2 sin . Die Oberfläche der Kugel
berechnet sich daher zu
6
5
( )
( )
%
2
%
5
" 4
5
det
B
" 1
( )
( )
%
2
"
( )
C
Zur Kontrolle, ob diese Definition sinnvoll sein kann, berechnen wir die
Oberfläche der Kugel: Hier ist, wie wir bereits wissen,
"
" 1
7
" 4
( ) ( )
7
" 4
5
( ) ( )
( )
6
" 4
7
soll dabei an Oberfläche erinnern.)
( )
"
7
det
bzw.
6
in
=
6 ( )
( )
(Das
e
e
C
( ) ( )
det
( )
%
( ) ( )
( )
5
( ) ( )
mit
7
=
"
bzw.
5
( ) ( )
Wenn wir die drei Komponenten von
bezeichnen, ist
6
.
ist
def
3
Kap. 2: Mehrdimensionale Analysis
7
=
Definition: Der Flächeninhalt eines Flächenstücks :
Höhere Mathematik I SS 2007
Ï B
Ï
0
0
@
* ,
* +
3
%4
%1
(
/
*
(
(
-
* ,
* +
"24
"21
3
(
/
*
)
Ï
Ï
)(
2
=(
Ï
Ï
@
Ï B
Ï
@
Ï B
@
@
Ï
|
Ï
Ï
@
@
Ï B
Ï B
Ï
Ï
Ï B
Ï B
2
) ,
|
@
@
$
Ï B
|
@
@
$
L
Ï
Ï B
Ï
Ï
@
Ï B
@
$
@
k
)
)2 =
2
.
4

×Ú $
k

4
$
L

k
4
4
e
e
h
h

3
Û
"
;
)
(2 + cos ) cos 2
(2 + cos ) sin 2
sin
+
+
3
×Ú $
ñ
+
9?:
$
N
"
,
+
$
M
3
<;=
,
,
9;:
,
+
"
"81
,
,
,
,
,
,
,
<
<
<
&
,
(0
,
M
<?=
+ ).
<;=
,
"24
,
"24
3
"21
3
M
,
"21
,
"24
3
,
" 1
Für Kurven hatten wir einerseits RIEMANN-STIELTJES-Integrale definiert,
die für eine beliebige Funktion auf der Kurve erklärt sind und in deren
Definition die Länge des Tangentenvektors eingeht; andererseits hatten
wir Integrale über Vektorfelder, in deren Definition der Tangentenvektor
selbst einging. Genauso gehen wir auch hier bei den Oberflächenintegralen vor, nur daß wir jetzt den Normalenvektor anstelle des Tangentenvektors benutzen:
es gibt also auf dem Mittelkreis keine eindeutig bestimmte Normalenrichtung.
+ )
9?:
(0
,
)=
(0
,
)
"84
(0
,
und damit
4 sin cos 2
4 sin sin 2
4 cos
9;:
)=
(0
"
,
)
,
(0
,
,
also
das durch Zusammenkleben der Enden eines einmal verdrillten rechteckigen Streifens
entsteht. Hier ist für = 0 nicht injektiv, denn (0 ) = (0 + ); wir haben also
kein reguläres Flächenstück. In der Tat wir für die Parameterwerte (0 ) der Mittelkreis
des Bandes zweimal durchlaufen. Dort ist
cos cos 2
4 sin 2
(0 ) = cos sin 2
und
(0 ) =
4 cos 2
,
sin
0
(
,
,
,
M
$
&
ì
<
1
D
Wenn wir von der Parameterdarstellung :
eines regulären
3
und einer festen Reihenfolge der Parameter ausgeFlächenstücks im
hen, können wir sogar unterscheiden, nach welcher Seite diese Richtung
[0 2 )
,
Eine für uns wichtige Besonderheit, die nur im 3 gilt, ist dagegen die
Tatsache, daß wir jedem Flächenstück eine eindeutig bestimmte Normalenrichtung zuordnen können: Im Dreidimensionalen gibt es nur eine
Richtung, die auf der Tangentialebenen eines Flächenstücks senkrecht
steht; in Dimension
3 gibt es dagegen einen ganzen (
2)dimensionalen Raum mit dieser Eigenschaft.
= [0 1]
Ý
:
<?=
Obwohl wir uns auf Flächen im 3 beschränken wollen, sei hier zumindest kurz darauf hingewiesen, daß wir bei der Herleitung dieser
neuen Darstellung des Flächeninhalts nirgends benutzen mußten, daß
wir im 3 sind; diese Formel gilt also auch für Flächenstücke im
mit
3.
4
3 ,
Im konkreten Fall steht hier natürlich genau dasselbe Integral wie bei der
Formel mit dem Betrag des Vektorprodukts, allerdings erfordert diese
Formel, sofern man die Fundamentalgrößen einer Fläche bereits kennt,
deutlich weniger Rechenaufwand. Dem Leser sei empfohlen, sich am
Beispiel der Kugeloberfläche hiervon zu überzeugen!
Typisches Beispiel eines nichtregulären Flächenstücks ist das MÖBIUS-Band
x
.
2
Die Fläche eines Flächenstücks kann also auch berechnet werden als
(
3 )(
(
DE
Damit können wir jedem Punkt eines regulären Flächenstücks eine eindeutig bestimmte Normalenrichtung zuordnen. Man beachte, daß dies
nur möglich ist aufgrund der Forderungen, die wir an ein reguläres
Flächenstück gestellt haben: Die Abbildung muß injektiv sein, so
daß die Parameterwerte (
) zu jedem Punkt des Flächenstücks eindeutig bestimmt sind, und
darf nirgends verschwinden, da der
Nullvektor keine wohlbestimmte Richtung hat.
4
Wir interessieren uns für das Parallelogramm mit Kantenvektoren
und
; hier wird diese Formel zu
@
)2 .
Ï
(
(
)
Ï B
)
4
)(
Ï B
)(
)
|
2
cos
x
(
$
=(
)(1
Ï B
=(
)(
) (
)(
) cos
und der Flächeninhalt selbst somit
2
Ï B
)(
Ï B
) sin
(
<
sich von der Fläche entfernt: Die Tangentialebene wird aufgespannt von
den partiellen Ableitungen und von nach den beiden Parametern
2
, und das Kreuzprodukt
auf
liefert einen Vektor,
der auf diesen beiden Tangentialvektoren und somit der gesamten Tangentialebenen senkrecht steht.
Kap. 2: Mehrdimensionale Analysis
der beiden Vektoren mal dem Sinus des eingeschlossenen Winkels .
Das Quadrat des Flächeninhalts ist also
Höhere Mathematik I SS 2007
%
<
<
1
D
y
e
e
h
G
G
!
h
h
3
3 x
3 4
e
3 y
e
O
D
y
¥
ÏÑÐ
e
h
y
e
Ï
h
3 D
!
Ï Ð
h
x
3 4
3 e
¥
Ï Ð
ÏÑÐ
O
<
<
D
B
@
3
Der Name Fluß für das unter b) definierte Integral wird klar, wenn man
sich etwa als eine Kugeloberfläche vorstellt. In jedem Punkt auf
dieser Oberfläche kann man ein kartesisches Koordinatensystem aus eiund zwei Tangenteneinheitsvektoren
nem Normaleneinheitsvektor
3
Ausgangspunkt ist ein reguläres Flächenstück :
; dessen
Bild = ( ), das eigentliche“ geometrische Flächenstück also, sei
”
3
als Rand.
beschränkt und habe eine reguläre Kurve : [ ]
Wie schon mehrfach erwähnt, wollen wir Kurvenintegrale längs mit
Oberflächenintegralen über oder – wie wir wegen der Parameterunabhängigkeit auch einigermaßen korrekt sagen können – in Verbindung bringen.
1
Eine unproblematische Verallgemeinerung des obigen Lemmas zeigt,
daß auch diese Integrale im dort definierten Sinne unabhängig von der
Parametrisierung sind.
durch die Oberfläche .
.
,
Wir beginnen mit letzterem sowie dem Satz von STOKES: Bei beiden geht
es darum, die Zirkulation eines Vektorfelds zu bestimmen. Beide Sätze
gelten in beliebiger Dimension, jedoch wollen wir sie der Einfachheit
halber nur für den 3 beweisen.
<
als den Fluß des Vektorfelds
e
)
Ï Ð
(
*
)
(
¥
)
4
(
=
x
def
In diesem Abschnitt geht es um drei der zentralsten Sätze der mehrdimensionalen Analysis: Außer den beiden im Titel erwähnten Sätzen soll
noch das mehrdimensionale Analogon des Hauptsatzes der Differentialund Integralrechnung bewiesen werden.
Ï æ
als Oberflächenintegral von über .
ein in einer Umgebung von ( ) definiertes Vektorfeld, so
b) Ist
bezeichnen wir
)
Ï æ
Ï Ð
4
(
G
)
x
(
h
)
¥
f) Die Sätze von Stokes und Gauß
=
=
e
G
(
\
Ï Ð
=
Ï
e
e
!
h
denn
Ï æ
e
!
def
Ï Ð
verankern. Drückt man nun den Vektor ( ) in diesem Koordinatensystem aus, so beschreibt die -Komponente jenen Teil des Vektors, der
durch die Kugeloberfläche hindurch nach innen oder außen geht (welches von beiden hängt ab vom Vorzeichen der Komponente und von der
Orientierung des Normaleneinheitsvektors), während die beiden anderen Komponenten den Teil beschreiben, der auf der Oberfläche bleibt,
also sozusagen den Fluß auf der Oberfläche im Gegensatz zum Fluß
durch die Oberfläche. Letzterer läßt sich berechnen als das Skalarpromit dem Normaleneinheitsvektor, und das Integral über
dukt ( )
diese Funktion ist
\
Ï
3
Definition: :
sei ein reguläres Flächenstück.
a) Ist eine auf ( ) definierte stetige Funktion, so bezeichnen wir
Kap. 2: Mehrdimensionale Analysis
Abb. 76: Das Möbiusband
Höhere Mathematik I SS 2007
ì
1
©
D
ì
<
1
×
ÏÑÐ
3
Wir gehen also aus von einem Vektorfeld :
, dessen (offener)
Definitionsbereich sowohl als auch enthält, und wollen Informa-
©
©
ì
×
\
Ï æ
.
ä
e
h
Ï Ð
Ô
Dazu approximieren wir durch ein Flächenstück , das wir aus endlich vielen ungefähr rechteckförmigen Teilmengen
zusammensetzen
können; ein grobes Bild einer solchen Unterteilung ist in Abbildung 77
zu sehen.
ì
=
e
«
l
,
bezeichnet. Natürlich ist erst
e
ä

ï
!
ì
e

h
e
ñå

h
e
PQ
«
R
ä
ì
1
,
wenn wir eine Formel für die einzelnen Rechtecke
haben, gilt diese
also automatisch auch für
und somit, nach einem Grenzübergang,
auch für .
=
ñå
=1
e
die Anzahl der Rechtecke“
wobei
”
recht für jede Funktion auf
Ï Ð
!
Betrachten wir also ein festes Rechteck
und das Kurvenintegral
entlang seines Umfangs. Da wir die Rechtecke als klein voraussetzen,
können wir ( ) auf
ohne großen Fehler linearisieren.
ì
\
ÏÑÐ
ì
8
\
8
ÏÑ
ÏÑ
\
ÏÑÐ
Ï Ð
Ï Ð
ÏÓ
n
0)
+ (
S
+ (
ÿ
x
\
Ï Ð
\
ÏÑÐ
\
\
für den symmetrischen Anteil der JACOBI-Matrix
+ rot (
\
+

0)
0)
ÿ
(
(
{
1
2
S
=
\
( 0) +
+ )=
ÏÑ
0
)
S
(
),
ÏÓ
{
n
wobei
Ï
( )=
\
(
0)
steht.
Dazu sei
ein beliebiger Punkt des Rechtecks. Ein beliebiger
Punkt
hat dann die Form =
+ mit einem nicht allzu
großen Vektor . Nach Definition der Differenzierbarkeit ist dann
Ï
S
In Abbildung 77 wurde davon ausgegangen, daß alle Normalenvektoren nach oben zeigen; der entsprechende Umlaufsinn ist für einige der
ï
Da als reguläres Flächenstück vorausgesetzt war, ist überall in
ein wohldefinierter Normalenvektor bestimmt; damit können wir auch
für jedes der Rechtecke einen Umlaufsinn festlegen: Dieser soll, wenn
man von der Spitze des Normalenvektors aus auf des Rechteck schaut,
der Gegenuhrzeigersinn sein. Da der Normalenvektor eines regulären
Flächenstücks stetig von den Parametern der Fläche abhängt und nirgends verschwindet, ist es gleichgültig, über welchem Punkt eines (hinreichend kleinen) Rechtecks wir ihn betrachten.
h
ÓÏ Ð
=1
Abb. 77: Unterteilung eines Bereichs
ì
h
........................
........
....
..........
....
.
.
........
.
.
..
.
..
.
.
.
.
.
.
...
.
.
.
.
.
.
..
..
.
.
.
.
.
..
..
....
..
....
..
........
...
..
..
..
....
...
.............
...
...........
..
......
...
....
...
...
...
...
...
...
.
....
..
......
.
.
.........
....
...........
.
..............
........
............
.................................................
Rechteckkanten eingezeichnet. Wie man sieht, wird jede gemeinsame
Kante zweier benachbarter Rechtecke von diesen beiden Rechtecken in
verschiedener Weise orientiert. Falls wir daher für jedes Rechteck
das Wegintegral entlang seines Rands berechnen und alle diese Integrale aufaddieren, bleiben nur die Integrale längs der in Abbildung 77 fett
ausgezogenen Kanten erhalten, d.h.
Kap. 2: Mehrdimensionale Analysis
tionen über das Kurvenintegral
Höhere Mathematik I SS 2007
\
ÿ
=
(
S
\
h
+ )
Ï +
h
e
+
1
2
ÏÑÐ
e
e
ÏÓÐ
e
\
Ï Ð
«
rot (
0)
,
h
h
n
h
e
#
Ï x
\
\
Ï \
Ï Ð
\
\
\
ÏÑÐ
q
Ð
:
Ð
\
\
ÏÑ
n
n

n
Ï n
21 )
+
13
+
2
n
n
+(
33
31 )
+
+(
23
n
q
:
nÏ 32 )
gleich dem Zweifachen dieses Vektorfelds.
n
+
2
:
12
22
n
+
q
n
n
=
Ð
:
n
ist wegen
Ð
+(
Ï Ð
2
Ð
ein Potentialfeld, denn der Gradient der quadrati-
~
T
T
j
j
*

*
q
: Ï Ð
q
Ï n
ÏÓÐ
Das Problem bei diesem Gegenbeispiel liegt also offensichtlich darin, daß der betrachtete Integrationsweg nicht als Rand eines regulären
Flächenstücks im Definitionsbereich des Vektorfelds geschrieben werden kann: Da das Vektorfeld auf der -Achse nicht definiert ist, muß der
Schnittpunkt mit der -Achse aus der Kreisscheibe herausgenommen
ì
<
1
×
Ï Ð
3
Satz: Das Vektorfeld :
habe eine symmetrische JACOBIMatrix, d.h. rot
sei identisch null. Dann gilt für jedes reguläre
q
Bei einem überall definiertes Vektorfeld hätten wir für einen solchen
Kreis einfach die geschlossene Kreisscheibe betrachten können, deren
Rand der betrachtete Integrationsweg ist, und nach obigem Satz wäre
das Integral längs des Randes verschwunden.
q
Damit haben wir (bis auf die hier unterdrückten, für einen richtigen
Beweis aber unbedingt notwendige Abschätzung der Fehlerterme) den
folgenden Satz bewiesen:
Damit sind also die beiden Vektorfelder ( 0 ) und
zirkulationsfrei,
und die Integrale über den (als Kurve geschlossenen) Rand von
verschwinden.
Diese Aussage ist aber leider falsch: Das Beispiel des Magnetfelds eines
stromdurchflossenen Leiters zeigte, daß die Rotation sehr wohl identisch
verschwinden kann, ohne daß das Vektorfeld zirkulationsfrei ist. Dieses
) = 2+ 2
ist allerdings auf der -Achse nicht
Magnetfeld (
definiert, und wir hatten im Beispiel Kreise um die -Achse betrachtet.

11
( 0) .

=
\
)=
ÏÑÐ
3
Dies reicht schon für den Hauptsatz der Differential- und Integralrechnung im 3 : Wir wissen bereits, daß ein Vektorfeld genau dann eine
Stammfunktion hat, wenn es zirkulationsfrei ist – die eine Richtung
dieser Aussage haben wir gerade wieder angewandt. Außerdem wissen wir, daß für ein Vektorfeld mit Stammfunktion die Rotation verschwindet, denn für eine zweimal stetig differenzierbare Funktion
ist rot grad = 0. Für ein leicht nachprüfbares Kriterium zur Existenz
einer Stammfunktion fehlt also nur noch die Aussage, daß aus dem
Verschwinden der Rotation die Zirkulationsfreiheit folgt.
<
Genauso ist auch
schen Form
+
Ð
2
©
+
ì
1
D
) = grad(
D
0)
×1
(
Ô
grad
Denn nach obiger Rechnung verschwindet bei symmetrischer JACOBIMatrix das Kurvenintegral entlang eines jeden Rechtecks, und die Summe all dieser Kurvenintegrale konvergiert bei immer feinerer Rechteckunterteilung des Flächenstücks gegen das Kurvenintegral längs des
Rands von = ( ).
ist,
©
Das erste Integral in dieser Summe ist ein Kurvenintegral über das konstante Vektorfeld, das jedem Punkt den Vektor ( 0 ) zuordnet. Dieses
Vektorfeld ist offensichtlich ein Potentialfeld, denn sind 1 2 und 3
die Komponenten dieses Vektors, so ist
= 0.
, dessen Rand eine Kurve
( )
wobei das um den negativ genommenen Ortsvektor von 0 verschobene Rechteck
sei, d.h., wenn den Rand von durchläuft, durchläuft
den
Rand
von .
+
0
0)
0
Flächenstück :
Kap. 2: Mehrdimensionale Analysis
h
ÏÑÐ
(
S
e
( )
Ï
) vernachlässigen, ist also
Wenn wir den Term (
Höhere Mathematik I SS 2007
q
q
ÏÑÐ
<
×
3
heißt
Definition: Eine offene zusammenhängende Teilmenge
einfach zusammenhängend, wenn jede geschlossene Kurve in Rand
eines regulären Flächenstücks ist. Anschaulich kann man dies auch so
interpretieren, daß die Kurve innerhalb von auf einen Punkt zusammengezogen werden kann: Man denke sich die Kurve als einen stark
angespannten Gummiring; wenn man diesen auf ein Flächenstück legt,
zieht er sich automatisch zusammen. Umgekehrt überstreicht der Ring
beim Zusammenziehen auf einen Punkt ein Flächenstück, dessen Rand
die Ausgangsposition des Gummis ist.
Um solche Fälle auszuschließen definieren wir:
E
×
©
×
<
×
ÏÓÐ
×
<
E
ÏÑÐ
h
e
<
1
Ï
Ï Ð
\
«
×
ÏÓÐ
×
<
þ
þ
Ð
Ð
@
1
2(
Ï
<
1
E
þ
$þ :
@
)
0)
;
.
1
2(
Ï b
x
Ï
@
,
wobei
Punkte auf der Kurve sind und die Tangentenvektoren in
diesen Punkten. Dieses Skalarprodukt eines Vektorprodukts mit einem
)
Nach Definition eines Kurvenintegrals ist das Integral hierüber Grenzwert einer Summe von Termen der Art
dann ist der Integrand
Ï x
Ï b
Auf höhere Dimension soll nicht genauer eingegangen werden; nur
soviel sei erwähnt: Die eindeutige Bestimmtheit des Normalenvektors
Ï Ð
Beweis: Dies folgt sofort aus dem Satz von GREEN.
e
h
dort identisch verschwindet, d.h. also, wenn die JACOBI-Matrix symmetrisch ist.
rot (
\
2
1
2
Ï Ð
wir müssen uns also dieses Integral genauer ansehen. Dabei setzen wir
zur Abkürzung
= rot ( 0 ) ;
( )
Damit genug zum ersten der drei Hauptsätze dieses Paragraphen; wir
machen weiter, wo wir vor der Spezialisierung auf symmetrische Vektorfelder aufgehört haben und folgern, daß nach ( ) für ein beliebiges
differenzierbares Vektorfeld gilt
E
1
:
auf einer einfach
hat genau dann eine Stammsymmetrisch ist.
ÏÑÐ
2
:
auf einer einfach
hat genau dann eine Stamm-
×
<
h
Ï x
2
×
Satz: Ein differenzierbares Vektorfeld
zusammenhängenden Teilmenge
funktion, wenn
×
1
#
Für ein ebenes Vektorfeld gilt entsprechend
E
Satz: Ein differenzierbares Vektorfeld
zusammenhängenden Teilmenge
funktion, wenn die JACOBI-Matrix von
<
Ï Ð
×
<
3
Satz: Ein differenzierbares Vektorfeld :
auf einer einfach
3
hat genau dann eine Stammzusammenhängenden Teilmenge
funktion, wenn rot dort identisch verschwindet, d.h. also, wenn die
JACOBI-Matrix symmetrisch ist.
Wenn man dann den einfachen Zusammenhang einer offenen zusamdadurch definiert, daß jede gemenhängenden Teilmenge
schlossene Kurve in Rand eines so orientierbaren Flächenstücks sein
soll, was auch wieder im wesentlichen äquivalent ist zur Zusammenziehbarkeit der Kurve, gilt auch hier der
<
Mit dieser Definition gilt dann offensichtlich die folgende Verallgemeinerung des Hauptsatzes der Differential- und Integralrechnung auf
den 3 :
eines Flächenstücks im 3 hat in höheren Dimensionen keine Entsprechung mehr; dort muß man von einem Flächenstück explizit fordern, daß
es orientierbar ist im folgenden Sinne: Man kann es durch kleine rechteckförmige Flächen überdecken und jedem dieser Rechtecke“ einen
”
Umlaufsinn zuordnen derart, daß die gemeinsame Kante zweier Nachbarrechtecke von diesen beiden Rechtecken entgegengesetzt orientiert
wird.
Kap. 2: Mehrdimensionale Analysis
werden, wir haben also nur noch einen punktierten Kreis, und dessen
Rand besteht aus der Kreislinie plus dem herausgenommenen Punkt.
Höhere Mathematik I SS 2007
b
\b
Ï @
Ï b
Ï
=(
b
)
Ï b
.
Ï
Ï
Ï
Ï b
@
Ï b
x
Ï b
Ï b
x
@
Ï b
Ï b
Ï b
Ï b
x
Ï b
©£ø
Ï )
<
r
©£ø
@
e
e
!
Ï
Ô é ¤U V

O
Ï )
Ï Ð
\
Ô é ¤U V
Ï Ð

Ï Ð
,
und für immer kleiner werdende Werte von stimmt dies immer besser
überein mit rot ( 0 ) mal dem Flächeninhalt der Kreisscheibe.
=
D
ÏÓÐ
Falls die Voraussetzungen dieses Satzes erfüllt sind, falls also insbesondere die Kreislinie Rand einer im Definitionsbereich von enthaltenen
Fläche ist, läßt sich die Rotation somit als Limes einer Art normierter“
”
Zirkulation auffassen, d.h. als Integral längs einer geschlossenen Kurve
dividiert durch die Länge dieser Kurve. Die Rotation gibt also auch ein
Maß für die Abweichung eines Vektorfelds von der Zirkulationsfreiheit.
×
1
×
×
ÏÑÐ
1
<
<
E
e
e
Ï
h
ÏÑÐ
!
.
r
ist Rand einer Kreisscheibe vom Radius mit FlächenBeweis:
inhalt 2 ; nach dem Satz von STOKES ist
Ï Ð
Ï )
h
rot
1
e
!
=

D
3
Satz von Stokes: :
sei ein differenzierbares Vektorfeld auf
3
. Weiter sei :
ein reguläres
der offenen Teilmenge
Flächenstück mit einer stückweise regulären Kurve als Rand. Dann ist
\
erklärt; wenn wir immer feinere Rechteckunterteilungen betrachten,
konvergiert die Summe der Kurvenintegrale über die Ränder dieser
Rechtecke also einerseits gegen das Kurvenintegral des Vektorfelds über
den Rand des betrachteten Flächenstücks, andererseits aber auch gegen das Integral der Rotation von über das Flächenstück selbst. Dies
ist der
Ï )
3
sei ein differenzierbares Vektorfeld, ein EinheitsSatz: :
vektor, und
ein Kreis mit Radius um 0 ist, der in einer Ebenen
senkrecht zu liege und von aus gesehen im Gegenuhrzeigersinn
durchlaufen werde; die gesamte von
berandete Kreisscheibe liege
in . Dann ist
1
rot ( 0 ) = lim 2
.
0
Aus dem Satz von STOKES können wir eine neue Charakterisierung der
Rotation herleiten:
h
rot
Der Vektor
steht senkrecht auf
und auf ; falls wir also
von einem flachen Rechteck ausgehen, steht er auch senkrecht auf diesem und hat somit die Richtung des Normalenvektors. Sein Betrag ist
gleich der Fläche des von
und aufgespannten Parallelogramms,
die Hälfte davon also gleich der Fläche des von diesen beiden Vektoren aufgespannten Dreiecks. Die Summe aller dieser Dreiecksflächen
ist im Limes gleich der Fläche des Rechtecks, über dessen Rand wir
integrieren, also ist das Integral über den Rand des Rechtecks für kleine
, wobei
Rechtecke näherungsweise gleich einem Skalarprodukt
als Länge den Flächeninhalt des Rechtecks hat und als Richtung die des
Normalenvektors. Als Grenzwert einer Summe solcher Skalarprodukte
ist aber gerade das Integral
)
Ï
(
GEORGE GABRIEL STOKES (1819–1903) wurde in Irland
geboren als jüngster von sechs Söhnen eines protestantischen Pfarrers. Nach dem Tod seines Vaters kam er
im Alter von 16 Jahren an eine Schule nach Bristol in
England und begann zwei Jahre später sein Studium an
der Universität Cambridge. Er wurde vor allem bekannt
durch seine Arbeiten zur mathematischen Physik, für
die er viele mathematische Techniken entwickelte. Er
gilt als der Begründer sowohl der Strömungslehre als
auch der Geodäsie und hatte unter anderem großen Einfluß auf die Entwicklung von MAXWELL. Ab 1849 lehrte
er als Professor an der Universität Cambridge.
Kap. 2: Mehrdimensionale Analysis
Vektor ist bekanntlich das Spatprodukt, und es ist gleich der Determinante mit den Spaltenvektoren
und . Diese Determinante ändert ihr
Vorzeichen, wenn man zwei Spalten vertauscht; tut man dies zweimal,
kehrt sie wieder zu ihrem alten Wert zurück. Daher ist
Höhere Mathematik I SS 2007
%
ÏÑÐ
©
e
¥
h
Ï Ð
Ô
<
×
ÏXW
×
D
1
1
e
Ï
Ï
\
e
D
ì
h
Ð
e
!
q
h
:
h
Ï
W
e
e
h
W
e
¥
,
Nun kommt die Differenzierbarkeit von
denn da alle Normalenvektoren nach außen zeigen, sind die linke und
die rechte Seite des Quaders verschieden orientiert.
$
Ð
\
Ï
Ï
W
Y
\
Ï
( )
ins Spiel und sagt uns, daß
+ (
)

)=
(
)+
ÏZW
þ
þ
q
: ÏZW
q
: ÏZW
Ï
+ ( ),
wobei die partielle Ableitung von
nach für jenes Vektorfeld stehen
soll, dessen Komponenten die partiellen Ableitungen der entsprechensind. Da wir in diesem Semester noch viel zu
den Komponenten von
tun haben, vernachlässigen wir den Term ( ) in der Hoffnung, daß er
für immer feiner werdende Unterteilungen trotz der dann ansteigenden
Anzahl dieser Terme keine Rolle mehr spielen wird.
JK
Ï JKJ
JKJKJ
( +
ist. Da der Vektor in Richtung der -Achse zeigt, können wir das (mit
=
) auch einfacher schreiben als
( )+
ÏXW
( + )=
{
ÿ
W
ÏXW
Ð
Ð
Ï
Ð
Ï ¢
ª
ª
In der Tat sollte ein mit den Abschätzungstechniken aus der Analysis I vertrauter Leser
keine Schwierigkeiten haben, dies mathematisch streng zu zeigen. Die Heuristik, nach der
man dabei vorgeht, ist (hoffentlich) klar: Die Anzahl aufeinanderliegender Quader in Richtung der -Achse ist proportional zu 1
, und 1
Terme der Größenordnung (
addieren sich zu einem Term der Größenordnung (1), d.h. zu einer Funktion, die gegen
Null geht. (Die Aussage geht schneller als 1 gegen Null“ ist natürlich gleichbedeutend
”
damit, daß die Funktion überhaupt gegen Null geht.)

\ 0
0
[
Ï k Ï :
ª
h
ÏXW
e
e
h
ÏXW
e
e
q
Ï
Ï
Ï
!
Ï
!
Ï
!
Ï
!
h
e
W
e
h
e
e
obere und
untere Seitenfläche
ÏXW
W
\
linke und
rechte Seitenfläche
h $
$
Ï
Ï
ÿ

vordere und
hintere Seitenfläche
Ï
( )
ÏXW
S
,
e
e
\
ÏÑ
+
ÏXW
h
ÿ
+
e
e
S
\ 0
0
=
\
!

Ein solcher Quader sei , und
seien die drei Kantenvektoren
von
in Richtung der -, - und -Achse. Dann ist das Integral von
gleich
über die Oberfläche von
h
Ï
Der Beweis des Satzes von GAUSS beruht auf derselben Idee wie der
des Satzes von STOKES: Dort hatten wir ein Flächenstück durch Rechtecke angenähert, um das Kurvenintegral längs seines Randes zu einem
Integral über das Flächenstück in Beziehung zu setzen; hier unterteilen
wir entsprechend das Volumen in kleine, der Einfachheit halber als
achsenparallel vorausgesetzte Quader, um das Oberflächenintegral über
den Rand von mit einem Integral über in Beziehung zu setzen.
e
!
h
( + )
\
( + )
Bemerkung: Der Satz gilt auch, mit den offensichtlichen Definitionen,
falls der Rand von
kein Flächenstück ist, sondern eine Fläche, die
aus endlich vielen regulären Stücken zusammengesetzt ist. Am Beweis
ändert sich dabei abgesehen vom größeren Schreibaufwand praktisch
nichts.
e
Ï
linke
Seitenfläche
e
linke
Seitenfläche
e
=
ÏXW
W
linke
Seitenfläche
Ï
( )
e
=
e
rechte
Seitenfläche
+
Ï
.
e
linke
Seitenfläche
h
ÏXW
!
!
div
h
ÏXW
!
=
Ï
=
Ï
!
linke und
rechte Seitenfläche
Ï
sei ein differenzierbares Vektorfeld und
Satz von Gauß: :
:
sei ein reguläres Flächenstück derart, daß = ( ) Rand
eines beschränkten dreidimensionalen Bereichs sei. Dann ist
und weiter ist beispielsweise
Kap. 2: Mehrdimensionale Analysis
Ï
3
Damit wäre auch der zweite Hauptsatz dieses Abschnitts bewiesen;
bleibt noch der
Höhere Mathematik I SS 2007
]
]
\ 0
0
[
W
W
ù«
q
: Ï ) *
$
h
e
Ï
e
Ï
e
!
ÏXW
Ï
Ï ) *
Ï
W
e
Í
q
þ
$
\
h
Ð
Ë
þ
: Ð
Ð
þ
þ
þ
ú úKúKúzúKÌ
K
e
e

$
Ï
W
e

þ
þ
e
þ
Ï ) *
h
W
h
þ
Ð
:
þ
e
e

ûKûKûKûzûKÎ
h
q
h
þ
q
e
e
Ð
e
e
k
Ï
!
ÏXW
þ
h
ÏXW
e
:
Ï
q
h
h
þ
Ð
e
e
¢
h
Ï
e
e
!
ÏXW
þ
!
e
ÏXW
e
:
ûKûzÎ
:
q
h
( ),
2
( ) und
3
( ).
^
þ
C
þ
e
e
þ
2
\
Ð
h
h
Ð
e
e

Ï
h
ÏXW
\
þ
þ
þ
:
è
!
þ
div
þ
ist, haben wir somit gezeigt, daß
3
ÏZW
( ) Vol(
( ) = div
\
( ) = div
( )+
Ð
( )+
Ð
1
( )
Ï
þ
Ð
C
q
h
:
e
Ð
h
C
)
( )
Das Oberflächenintegral über die gesamte Quaderoberfläche ist die Summe dieser drei Teilintegrale, und da bekanntlich
h
þ
( ).
e
=
e
!

ª
\
q
þ
e
þ

linke
Seitenfläche
Ï
k_
( )
=

\
1
k_
þ
q
1
h
þ
\
linke
Seitenfläche
^
linke und
rechte Seitenfläche
1
1
\
obere und
untere Seitenfläche

vordere und
hintere Seitenfläche
k_
þ
Ð
Nach dem Mittelwertsatz für Flächenintegrale können wir diese Integrale weiter abschätzen: Es gibt Punkte auf der linken, auf der vorderen
und auf der unteren Seitenfläche, so daß
ÏXW
linke und
rechte Seitenfläche
e
.
Wenn wir das alles glauben, ist also
þ
:
obere
Seitenfläche
\
úKúzÌ
\
obere und
untere Seitenfläche
Ë
!
3
h
Ï
þ
Ð
vordere
Seitenfläche
Í
þ
vordere und
hintere Seitenfläche
^
und
!
:
!
\
2
h
Ð
Ð
Ganz entsprechend ist
h
.
Ï
C linke
Seitenfläche
ª
0
e
1
ÏXW
0
e
C 1
h
h
è
=
Ï
h
!
linke
Seitenfläche
Ï
è
linke
Seitenfläche
h
1
e
1
\
Nun ist es wieder an der Zeit, eine etwas komplexere Abschätzung unter
und liegen auf den Seiden Tisch fallen zu lassen: Die Punkte
tenflächen eines Quaders, der immer kleiner werden soll. Damit rücken
auch diese Punkte immer weiter zusammen und wir sollten wohl keinen
allzu großen Fehler machen, wenn wir einfach irgendeinen Punkt
im Quader
auswählen und sowohl
als auch durch diesen
Punkt ersetzen; die formale Rechtfertigung hierfür geht wieder aus von
und beruht im übrigen auf
der Differenzierbarkeit des Vektorfelds
Abschätzungen.

=
k_
=
þ
q
1

obere und
untere Seitenfläche
k_
( ).
^
linke
Seitenfläche
ÏXW
3
linke und
rechte Seitenfläche
e
þ
Ð
,
( )
:
( )
2
è
( + )
und
!
vordere und
hintere Seitenfläche
Ï
þ
=
Genauso ist
Kap. 2: Mehrdimensionale Analysis
þ
Ð
und damit
Der Einheitsnormalenvektor der linken Seite des Quaders zeigt in Richtung der negativen -Achse, denn die linke Seite ist parallel zur ( )Ebene und zeigt nach außen. Wenn wir den Einheitsvektor der -Achse
mit bezeichnen, ist daher
Höhere Mathematik I SS 2007
#
ÏXW
ÏXW
k_

h
ÏXW
!
e
e
ù«
k_

:
:
ª
Ï
\
Ï
( ) Vol(
Ð
ª
),
h
h
h
W
q
:
W
ª
Ð
D
Im Falle des Integrals über die Randfläche
= ( ) von
ist die
Situation etwas komplizierter: Wie beim Beweis des Satzes von STOKES
überlegt man sich zunächst leicht, daß eine gemeinsame Seitenfläche
zweier benachbarter Quader von den beiden Quadern verschieden orientiert wird, so daß sich die beiden Integrale über diese Fläche gegenseiist
tig aufheben; die Summe über alle Oberflächenintegrale über die
also gleich der Summe über alle Oberflächenintegrale über jene Seiten, die nur Seitenfläche eines einzigen Quaders
flächen von Quadern
sind, d.h. also über die Randfläche der Vereinigung aller Quader .
ª
ª
ì
ì
\
Ï
Ï

Ï
\
ÏZW
Ï
1 1)
+
W
Ï )
2 2)
+
\
\
ÏXW
W
( ) (
W
\
( ) (
Ï
\
( ) (
Ï
3 3
\
+
8
2 2

=
ÏXW

+
ì
3 3) ;
Ï
1 1
ì
r
=
ì
,

ist
Beweis: Nach dem Mittelwertsatz ist das Volumenintegral über gleich
dem Produkt des Volumens 43 3 von
mit dem Wert des Integranden
div
an einem geeigneten Punkt der Kugel. Falls gegen Null geht,
muß dieser Punkt immer näher an den Mittelpunkt der Kugel rücken,
bis er im Limes mit diesem zusammenfällt.

( )
ÏXW
ì
Dann ist
\
.
r
3
!
\
2

ì
3
ñ ¤
1
( )=
e
und
ÏXW
2
e
ist, deren Normalenvektoren
h
1
3
!
0
W
Ï
um
1
wobei
eine Kugel mit Radius
nach außen zeigen.
:
×
Satz: Für ein differenzierbares Vektorfeld
3
div ( 0 ) = lim
3
0 4
Genau wie der Satz von STOKES zu einer alternativen Definition der
Rotation führte, kann mit dem Satz von GAUSS die Divergenz auf andere
Weise ausgedrückt werden; zumindest für Quader haben wir die entsprechende Formel im gerade beendeten Beweis als Formel ( ) bereits
hergeleitet:
#
=
Wie wir oben gesehen haben, ist der Satz für einen einzelnen Quader
richtig; da auf beiden Seiten das Integral durch Summen entsprechender
Integrale für Quader angehähert werden kann, ist also der Satz von
GAUSS (modulo zahlreicher Auslassungen) bewiesen.
ì
Ï
<
Der Integrand bei einem Oberflächenintegral über ein Vektorfeld ist das
Skalarprodukt aus dem Normalenvektor von im jeweils betrachteten
Punkt und dem Wert ( ) des Vektorfelds in diesem Punkt. Konkret
sei etwa der Normalenvektor im Punkt
, und in Koordinaten sei
\
Die Quaderflächen, die diesen Rand ausmachen, sind allesamt parallel
zu Koordinatenebenen; ihre Normalenvektoren sind also parallel zu Koordinatenachsen, wohingegen die Normalenvektoren von
natürlich
beliebige Richtungen haben können. Wir müssen uns überlegen, warum
die Integrale im Limes trotzdem gleich sein können.
ì
Falls drei nichtverschwindende Komponenten hat, ist klar, daß die
Fläche in der Nähe von nur so durch Quader angenähert werden
kann, daß es dort freie Randflächen parallel zu allen drei Koordinatenebenen gibt; ein nicht allzu schwieriges Argument über den Satz von
PYTHAGORAS zusammen mit Limesbetrachtungen zeigt, daß auch mit
den Längen alles gut geht, so daß auch das Oberflächenintegral über
gleich der Summe der Integrale über die Quaderoberflächen ist.
Ï
und wenn wir die Quader immer weiter verkleinern, wird im Limes
aus dem Ungefährzeichen ein Gleichheitszeichen – genau so hatten wir
schließlich Volumenintegrale definiert.
e
e
e
div
ÏXW
div
\
wir erhalten also dasselbe Skalarprodukt auch, indem wir ( ) nacheinander mit geeigneten Normalenvektoren von Quaderflächen parallel
zu den Koordinatenebenen multiplizieren und die Ergebnisse aufaddieren.
Kap. 2: Mehrdimensionale Analysis
Damit haben wir eine lokale Version des Satzes von GAUSS gezeigt;
zum Beweis des Satzes selbst nähern wir das Volumen an durch die
Quader . Dann ist
ist.
Höhere Mathematik I SS 2007
%
r
r
W
Ï )
Ï )
Ð
%
Auch der Satz von GAUSS läßt sich wieder anschaulich interpretieren:
Bei der Definition der Divergenz haben wir uns bereits überlegt, daß
diese mißt, inwieweit ein Punkt eher eine Quelle oder eine Senke für
ein Vektorfeld ist. Da das Oberflächenintegral gerade gleich dem Fluß
des Vektorfelds durch die betrachtete Oberfläche ist und wir die Oberfläche so orientiert haben, daß der Normalenvektor nach außen zeigt,
sagt der Satz von GAUSS also einfach, daß der gesamte Fluß einer Vektorfelds durch die Oberfläche eines Volumens genau das ist, was im
Innern von erzeugt oder (bei negativen Vorzeichen auf beiden Seiten)
vernichtet wird.
Höhere Mathematik I SS 2007
Ð
Der obige Satz zur Charakterisierung der Divergenz zeigt dementsprechend noch einmal, warum die Divergenz auch als Quellendichte bezeichnet wird: Nach dem Satz von GAUSS ist der Fluß durch die Oberfläche einer Kugel gleich der Summe des im Innern erzeugten oder
vernichteten; dividiert man dies durch das Volumen der Kugel, entsteht
die Quellendichte, deren Grenzwert für immer kleiner werdende Kugeln
gleich der Divergenz ist.
¨
Kap. 2: Mehrdimensionale Analysis
!
%
a
`
h
g
`
`
b
f
a
`
a
`
e
d
Ò
c

Zugehörige Unterlagen

Differentialgeomtrie W 16/17, ¨Ubungen 6 Es sei M ⊂ R 3 eine

UE 7

Blatt 7 - Fachbereich Mathematik

Also ist 1 sec ) + sec . Da wir sow ohl sec ) = 0 m als auch die W erte

Zugehörige Unterlagen

Produkte

Unterstützung

Also ist 1 sec ) + sec . Da wir sow ohl sec ) = 0 m als auch die W erte

Zugehörige Unterlagen

Dieses Dokument Sammlung (en)

Dieses Dokument gespeichert

Schlagen Sie uns vor, wie wir StudyLib verbessern können