Bestimmung Angebotsfunktion - karl
Werbung

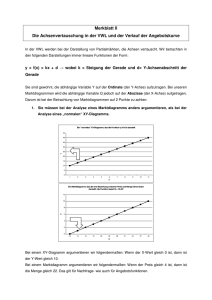
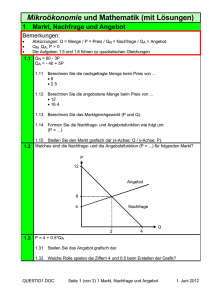
Fachhochschule Meschede VWL für Ingenieure Dr. Betz Aufgabe Bestimmung Angebotsfunktion, Marktgleichgewicht und Steuerinzidenz Als Vorstandsmitglied im Bereich Finanzen / Steuern der Elektro AG sind Sie hauptverantwortlich für die Preiskontrolle Ihrer Produkte. Ihr Hauptfokus liegt in der Herstellung von Waschmaschinen. Marktforschungen haben ergeben, dass die Zahlungsbereitschaft der Nachfrager bei einem Preis von 1.500 € erlischt und zu diesem Preis keine Maschine mehr abgesetzt werden kann. Außerdem wurde herausgefunden, dass bei minimalstem Preis maximal 15.000 Maschinen nachfragt werden. Da sich noch mehrere Hersteller von Waschmaschinen im Markt befinden, können Sie nicht einen Preis durchsetzen sondern haben nur die Möglichkeit Ihre Maschinen zum Marktpreis zu verkaufen. Dieser Marktpreis ergibt sich durch den Schnittpunkt der Nachfrage- und der Angebotskurve aller Anbieter. Auch hier haben Sie durch Marktbeobachtungen folgendes festgestellt: Bei einem Preis von 200 € ist kein Anbieter bereit eine Waschmaschine herzustellen. Bei einem Preis von 1.800 € lassen sich Anbieter finden, die insgesamt eine Menge von 10.000 Waschmaschinen anbieten. Fragen: a) Wie lauten die Angebots- und Nachfragefunktionen xAT und xNT? (Unterstellen Sie jeweils einen linearen und kontinuierlichen Verlauf) b) Stellen Sie die Funktionen in einem geeigneten Diagramm dar. Bestimmen Sie den Gleichgewichtspreis und die Gleichgewichtsmenge grafisch und algebraisch! c) Um den Konsum von Waschmaschinen zu dämpfen, beschließt der Staat eine Steuer auf eben diese. Wie wirkt sich eine Steuer von 260€ pro Waschmaschine auf Angebots- und Nachfragekurve, sowie auf das Marktgleichgewicht aus? Zeigen Sie grafisch und algebraisch die Veränderungen! Gehen Sie davon aus, dass der Anbieter die Steuer entrichten muss. Antworten: a) Die Allgemeine Angebotsfunktion lautet x = mp + b. Begriffserklärung: x ist die nachgefragte bzw. angebotene Menge m ist die Steigung der jeweiligen Funktion p ist der Preis b ist der jeweilige Achsenabschnitt der x-Achse 1.Festlegen der Punkte der Nachfragefunktion: P1 : Bei 1500€ werden 0 Stück nachgefragt => x=0, p=1500€ P2 : Bei 0€ werden 15.000 Stück nachgefragt => x=15.000Stk., p=0€ 2.Festlegen der Punkte der Angebotsfunktion: P1: Angebot von 10.000 Stück bei 1.800€ => x=10.000Stk., p=1800€ P2: Angebot von 0 Stück bei 200€ => x=0, p=200€ 3.Bestimmung der Nachfragefunktion: x = mp + b i. 0Stk. = m*1500€ + b ii.15.000Stk. = m*0+b i. 0 -10 => = = m*1500€ + 15.000Stk.| - 15.000Stk. | :1500€ m XNE = 15.000 Stück – 10*p 4.Bestimmung der Angebotsfunktion: x = mp + b i.10.000Stk. = m*1800€ + b ii. 0Stk. = m*200€+b => 10000Stk. = 6,25 = iii. 0 = -1250Stk. = => => b=15.000 Stück | | i. - ii. m*1600€ m | :1600€ 6,25*200+b b |-1250 Stück XAT = -1250 Stück + 6,25*p Zur Vorstellung wo die Punkte liegen, könnte es hilfreich sein die Punkte in ein Koordinatensystem einzutragen. b) Um das Marktgleichgewicht algebraisch zu bestimmen setzen wir die Angebots- und Nachfragefunktion gleich. Ermittlung von x* und p*. XAT = -1250 Stk. + 6,25p* = 16,25p* = p* = XNE 15.000 Stk. – 10p* 16.250Stk. 1000€ |+10p* | +1250Stk. | : 16,25Stk./€ x* = -1250 Stk. + 6.25 p* x* = -1250 Stk. + 6.25 * 1000 x* = 5000 Stk. Das Marktgleichgewicht liegt bei 5000 Waschmaschinen, jeweils zum Preis von 1000€. Um das Marktgleichgewicht grafisch zu bestimmen setzen wir in die Angebots- und Nachfragefunktion bestimmte Werte und ermitteln so Punkte um die Geraden der Funktionen zeichnen zu können. Der Schnittpunkt der beiden Geraden gibt unser Marktgleichgewicht wider. Ermittlung von x* und p*. 1.Bestimmung der Punkte für die Angebotsfunktion : XAT = -1250 Stück + 6,25*p P1 = -1250 Stück + 6,25*1800€ = 10.000 Stück => P1 = (10.000 Stück | 1800€) P2 = -1250 Stück + 6,25*(-200€) = -2.500 Stück => P2 = (-2.500 Stück | -200€) 1.Bestimmung der Punkte für die Nachfragefunktion : XNE = 15.000 Stück – 10*p P1 = 15.000 Stück – 10*1520 € = -200 Stück => P1 = (-200 Stück | 1520€) P2 = 15.000 Stück – 10*0 € =15.000 Stück => P1= (15000 Stück | 0€) Das Marktgleichgewicht ergibt sich so aus dem Punkt: x * = 5000 Stück. und p* = 1000€. c) Die Nachfragekurve ändert sich nicht, da in der Aufgaben Stellung steht, dass die Anbieter die Steuern zahlen müssen. Folge : Neue Kurve der Angebotsfunktion. Angebotsfunktion ohne Steuern : XAT = -1250 Stk. + 6,25p. Angebotsfunktion mit Steuern : XAT = - 1.250 Stk. + 6,25(p-260€). = -2.875 Stk. + 6,25p Weil die Anbieter die Steuern zahlen müssen wird weniger angeboten. Also erst ab einen höheren Preis werden Anbieter bereit sein Maschinen anzubieten. Deshalb wird der Preis minus die Steuern gerechnet. Zur algebraischen Lösung : XAT = -2.875 Stk. + 6,25pK* = 16,25pK* = pK* = XNE 15.000 Stk. – 10pK* 17.875 Stk. 1100€ |+10pK* |+2.875 Stk. | : 16,25Stk./€ x1* = -2.875 Stk. + 6.25 pK* x1* = -2.875 Stk. + 6.25 * 1100€ x1* = 4000 Stk. Das Marktgleichgewicht liegt bei 4.000 Waschmaschinen, jeweils zum Preis von 1100€. Zur grafischen Lösung : Bestimmung der Punkte für die neue Angebotsfunktion : XAT = -2.875 Stk. + 6,25p P1 = -2.875 Stk + 6,25*1800€ = 8.375 Stück => P1 = (8.375 Stück | 1800€) P2 = -2.875 Stück + 6,25*(-200€) = -4.125 Stück => P2 = (-4.125 Stück | -200€) Begriffserklärung: PK* = Preis den die Nachfrager bezahlen. PV* = Preis den die Verkäufer erzielen. X1* = Neues Mengengleichgewicht. => 1.110€ => 840€ => 4.000 Stück Diese Punkte ergeben sich aus den Schnittpunkten der Angebotskurve und der Nachfragekurve. Das Marktgleichgewicht wird bestimmt, aus dem neuen Schnittpunkt der Nachfragekurve und der neuen Angebotskurve und setzt sich aus: PK* = 1.110€ und X1* = 4.000 Stück zusammen. Im Endeffekt verschiebt sich also das Marktgleichgewicht. Es muss für eine Waschmaschine mehr bezahlt werden und deshalb wird auch weniger gekauft. Desweiteren sieht man, dass die Steuern durch Steuerinzidenz nicht komplett auf die Anbieter zurückfallen, sondern auch ein Teil auf die Käufer zukommt. Am Ende bezahlt der Käufer 1.100€ anstatt 1.000€ und der Verkäufer erhält anstatt 1.000€ nur noch 840€. In der Aufgabe hieß es jedoch, dass die Anbieter die Steuern zu tragen hätten, was jedoch, nicht vollkommen zutrifft. Desweitern verringert sich auch die angebotene Menge an Waschmaschinen von 5.000 Stück auf 4.000 Stück. Außerdem sieht man, dass die Anbieter bereit sind erst ab einen Preis von 460€ Waschmaschinen anzubieten und nicht wie ohne Steuern bereits ab 200€. Anmerkung: Man hätte auch bei der Steueraufgabe die Nachfragekurve verschieben können und so die Käufer die Steuern zahlen lassen. Das Ergebnis wäre das gleiche gewesen wie bei der Verschiebung der Angebotskurve. Ich wollte jedoch nur eine Musterlösung vorstellen und habe deshalb nach der Angebotsfunktion gefragt.