Die Achsenvertauschung in der VWL

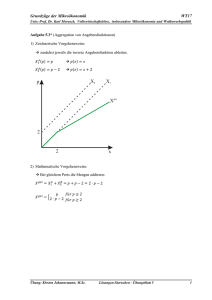
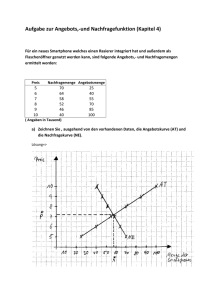
Merkblatt II
Die Achsenvertauschung in der VWL und der Verlauf der Angebotskurve
In der VWL werden bei der Darstellung von Partialmärkten, die Achsen vertauscht. Wir betrachten in
den folgenden Darstellungen immer lineare Funktionen der Form:
y = f(x) = kx + d
wobei k = Steigung der Gerade und d= Y-Achsenabschnitt der
Gerade
Sie sind gewohnt, die abhängige Variable Y auf der Ordinate (der Y-Achse) aufzutragen. Bei unseren
Marktdiagrammen wird die abhängige Variable Q jedoch auf der Abszisse (der X-Achse) aufgetragen.
Darum ist bei der Betrachtung von Marktdiagrammen auf 2 Punkte zu achten:
1. Sie müssen bei der Analyse eines Marktdiagramms anders argumentieren, als bei der
Analyse eines „normalen“ XY-Diagramms.
Ein "normales" XY-Diagramm, das die Funktion y=10+3x darstellt
45
40
35
30
Y
25
20
15
10
5
0
1
2
3
4
5
6
7
8
9
10
11
X
Ein Marktdiagramm, das die eine Beziehung zwischen Preis und Menge eines Gutes
darstellt; die Funktion lautet Q = 10+3P
12
10
P
8
6
4
2
0
10
13
16
19
22
25
28
31
34
37
40
Q
Bei einem XY-Diagramm argumentieren wir folgendermaßen: Wenn der X-Wert gleich 0 ist, dann ist
der Y-Wert gleich 10.
Bei einem Marktdiagramm argumentieren wir folgendermaßen: Wenn der Preis gleich 4 ist, dann ist
die Menge gleich 22. Das gilt für Nachfrage- wie auch für Angebotsfunktionen.
2. Die Ausprägung der Funktion muss umgekehrt interpretiert werden.
Eine Angebotsfunktion: Q=10+5P
12
10
8
6
P
4
2
0
0
5
10
15
20
25
30
35
40
45
50
55
60
-2
-4
Q
Eine Angebotsfunktion: Q=5P-10
12
10
P
8
6
4
2
0
0
5
10
15
20
25
30
35
40
Q
Eine Angebotsfunktion: Q=5P
12
10
P
8
6
4
2
0
0
5
10
15
20
25
30
35
40
Q
Wichtig:
Angebots- und Nachfragefunktionen sind nur für positive Werte definiert.
Eine Angebotsfunktion der Form
Q=kx+d schneidet die X-Achse! (unelastisch)
Q=kx-d schneidet die Y-Achse! (elastisch)
Q=kx beginnt im 0-Punkt! (iso-elastisch)
45
50